车轮载荷对其残余应变应力分布特性的影响
2016-05-08于荣泉任尊松孙守光
于荣泉, 任尊松, 孙守光
(北京交通大学 轨道车辆结构可靠性与运用检测技术教育部工程研究中心, 北京 100044)
轮轨滚动接触疲劳破坏现象随着铁路客货运量的增大和列车速度的提高变得越来越严重,目前已成为影响和制约轮轨服役寿命和运输安全的重要因素,是轮轨的主要失效形式之一[1]。1998年德国汉堡开往慕尼黑的ICE高速列车因低噪声弹性车轮崩裂而脱轨撞桥,造成严重脱轨事故。2000年,一列高速列车从伦敦驶往Leeds的途中,由于曲线外侧钢轨疲劳裂纹扩展导致钢轨断裂造成出轨事故。由此可见研究轮轨滚动接触疲劳损伤问题以降低由滚动接触疲劳造成的列车事故具有重要的工程意义。滚动接触弹塑性应力应变分析是研究轮轨滚动接触疲劳失效的基础和关键。
目前国内外学者利用有限元方法对滚动接触弹塑性应力做了很多研究。文献[2-3]利用有限元软件ABAQUS建立非稳态载荷作用下钢轨弹塑性二维有限元模型,并分析了波状表面波谷和波峰处的残余应力和残余应变;文献[4]建立了轮轨接触热弹塑性平面应变热机耦合二维有限元模型,分析摩擦生热对轮轨热弹塑性的影响;文献[5]用有限元方法建立了钢轨三维弹塑性滚动接触计算模型,模型中采用双线性随动硬化弹塑性本构模型,分析了钢轨材料屈服强度对钢轨残余应力和应变的影响;文献[6]利用有限元参数二次规划法进行不同轮径、轴重和摩擦系数等工况下弹性和弹塑性计算,得出轮轨间接触状态和接触内力的分布情况;文献[7]建立基于ALE有限元方法的稳态轮轨滚动接触的三维有限元模型,该模型在虚功率方程中通过Lagrange乘子法引入接触界面上无切向滑移约束,计算分析接触斑的黏着特性;文献[8]利用有限元方法,采用非线性各向同性随动硬化模型,对循环载荷作用下钢轨材料的棘轮效应进行分析。以上研究仅局限于轮轨接触中钢轨的弹塑性应力应变及接触状态和黏着特性的分析,有关车轮三维弹塑性应力应变分析的文献较少。文献[9]研究了车轮三维滚动接触状态下等效塑性应变和静水压力等随轴重和温度的变化规律,但没有分析车轮表面附近残余应力和残余应变分布特性及随循环载荷的累积规律。
鉴于此,本文运用有限元方法建立车轮三维滚动接触弹塑性有限元计算模型,模型中采用Lemaitre-Chaboche非线性各向同性随动硬化循环塑性模型,研究在循环载荷作用下,最大接触压力和切向力对车轮接触表面附近材料的残余应力和残余应变分布特性及累积规律的影响。
1 数值计算模型
1.1 三维滚动接触
利用ABAQUS软件建立车轮三维弹塑性有限元模型。模型中不考虑循环载荷作用下车轮接触表面材料塑性变形对接触边界条件的影响,轮轨表面接触压力和接触斑形状大小依据Hertz接触理论计算[10]。
Hertz接触理论中接触斑法向接触压力分布(以接触斑中心为原点,车轮周向为x轴方向,轴向为y轴方向,见图1。接触压力为

( 1 )
式中:px,y为椭圆接触斑内任意点的接触压力;x和y分别为接触斑周向和轴向坐标;a和b为椭圆形接触斑长短半轴,a、b具体值由轮轨接触几何参数和轮轨力确定[11]。
( 2 )
式中:p0为接触斑最大接触压力;Fn为轮轨接触力。
车轮椭圆接触斑长半轴和短半轴大小为
( 3 )
( 4 )
式中:mH、nH为赫兹接触系数,与(B-A)/(B+A)的值有关;A、B为相对曲率,具体表达式见文献[11];kH1和kH2是与轮轨材料相关的常数,为
( 5 )
( 6 )
式中:E1和E2分别为车轮和钢轨材料的弹性模量,取为210 GPa;v1和v2分别为车轮和钢轨材料的泊松比,取为0.3。
轮轨几何尺寸分别为:车轮滚动圆半径R11为420 mm,车轮踏面横向圆弧半径为无穷大,钢轨纵向曲率半径为无穷大,钢轨横向曲率半径R22为300 mm。
轮轨接触斑内切向力分布不考虑接触斑黏着区和滑动区的影响,假设切向力正比于法向压力。
Qx=μP
( 7 )
式中:Qx为x向切向力;μ为全滑动摩擦因数;P为法向接触压力。
1.2 有限元网格及其边界条件
通过非线性软件ABAQUS建立车轮三维弹塑性有限元模型,为了提高分析效率和节约计算成本,选取车轮圆心角为15°的扇形区域作为车轮计算模型,见图2(a)。通过试算,循环载荷对车轮材料弹塑性影响主要分布在车轮表面及表面下15 mm深度范围内,在该范围内进行网格细化处理,在车轮表面径向深度15 mm,轴向宽度35 mm的范围内采用单元尺寸为1 mm的正六面体缩减积分单元,远离接触面的区域采用较粗的网格进行处理,网格划分细节见图2(b)。车轮扇形有限元计算模型,径向侧面边界节点采用周向和轴向位移约束边界,轮毂与车轴配合表面节点采用位移全约束边界。

1.3 材料本构模型
材料本构模型采用Lemaitre-Chaboche非线性各向同性随动硬化循环塑性模型[12],该模型能够合理地描述滚动接触条件下材料循环塑性的应力松弛和棘轮效应。材料参数采用铁路工业常用的BS11普通车轮钢,车轮钢材料参数参见表1。
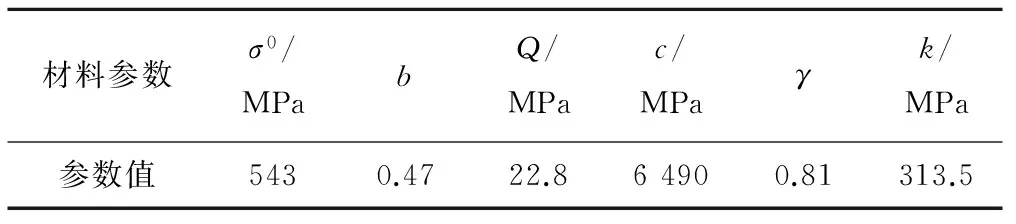
表1 车轮钢循环塑性模型材料参数[13-14]
1.4 模型计算参数
为了计算和表达方便,文中对长度、应力和应变变量分别用a0、k和k/G进行无量纲化处理,a0为接触斑长轴之半,k和G分别为剪切屈服强度和剪切弹性模量。
车轮三维弹塑性有限元模型主要分析循环接触载荷反复作用下最大接触压力p0和切向力Qx对车轮接触表面及附近材料残余应力和残余应变分布特性及累积规律的影响。选取轴重21、25、30 t,摩擦因数0、0.1、0.3、0.5分别进行计算。
轴重21、25、30 t分别用最大接触压力p0=3.97k、4.21k、4.47k表示;摩擦因数0、0.1、0.3、0.5分别表示Qx为0、0.1P、0.3P、0.5P。由式( 3 )和式( 4 )得到,p0=4.21k时接触斑长轴之半为a0=7.1 mm。对车轮接触表面及附近材料残余应力和残余应变分布特性及累积规律的影响。选取轴重21、25、30 t,摩擦因数0、0.1、0.3、0.5分别进行计算。
2 结果分析
考虑到轮轨滚动接触三维弹塑性有限元分析的困难性和计算量巨大,文中对每种载荷工况循环计算10次。
2.1 滚动接触弹塑性分析
图3和图4分别给出了p0=4.21k、Qx=0.3P工况下,接触斑中心深度为z=0.067a0处应力、应变在第一次循环载荷作用下随载荷步的变化。从图3、图4中可以看出,经历第一次循环载荷作用后,车轮三维滚动接触状态下6个残余应力分量和6个残余应变分量均不为零,这与文献[15]分析结果一致。本文重点分析周向残余应力σxr、轴向残余应力σyr、残余剪切应变γxzr随循环载荷的变化情况。
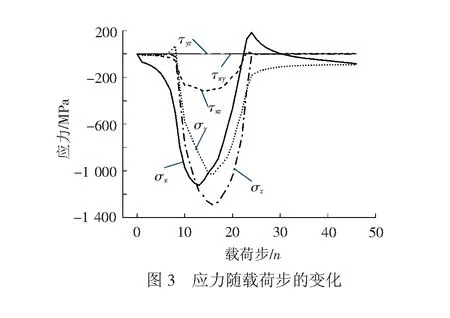

图5给出了p0=4.21k、Qx=0.3P工况下,σxr、σyr随深度分布的累积情况。由图5中可以看出,最大残余应力σxr和σyr分别发生在车轮次表面z/a0=0.6和z/a0=0.4处。周向和轴向残余应力在接触表面和次表面均为残余压应力。

图5(a)中,当z/a0>1.1时,产生周向残余拉应力;图5(b)中,当z/a0>0.9时,产生轴向残余拉应力。从图5中可以看出,经过10次循环载荷作用后,残余应力逐渐趋于稳定。
图6给出了p0=4.21k、Qx=0.3P工况下,γxzr随深度的分布累积情况。从图中可以看出,最大残余剪切应变发生在接触表面,且残余剪切应变主要分布在接触表面至z/a0=1范围内。残余剪切应变随循环载荷作用次数的增加而逐渐增大,但增长率随循环载荷作用次数的增加而逐渐衰减。

2.2 最大接触压力影响
最大接触压力分别为p0=3.97k、4.21k和4.47k时,循环载荷作用10次后σxr、σyr随深度的分布情况见图7。
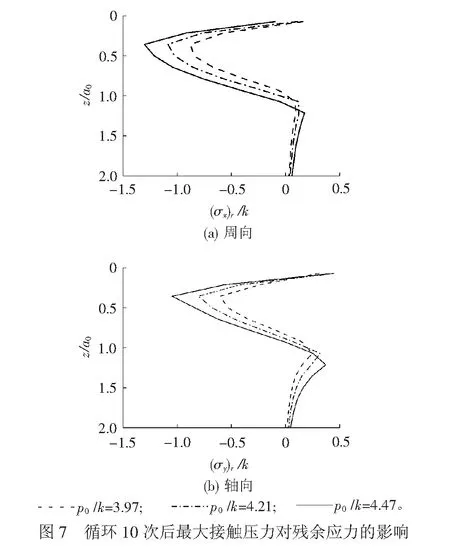
图7(a)和图7(b)分别为σxr和σyr的分布情况。从图中可以看出,最大接触压力对残余应力分布的影响较大。周向和轴向最大残余应力均发生在次表面z/a0=0.35处,且随着最大接触压力的增加而增大。
图8所示为循环载荷作用10次后最大接触压力对残余剪切应变的影响。由此可见,最大接触压力作用下最大残余剪切应变均发生在z/a0=0.5处,且随着最大接触压力的增加而增大。

2.3 切向力影响
图9(a)和图9(b)分别给出了循环载荷p0=4.21k作用10次后,切向力对周向残余应力σxr和轴向残余应力σyr的影响。从图9(a)中可以看出,切向力对周向残余应力σxr分布的影响显著。切向力为0P、0.1P和0.3P时,残余应力σxr最大值均发生在次表面,且切向力为0P和0.1P时发生在次表面z/a0=0.36处,切向力为0.3P时发生在次表面z/a0=0.64处。当切向力为0.5P时,残余应力σxr最大值发生在车轮接触表面。

由图9(b)可得到,相比于图9(a),在不同切向力作用下,轴向残余应力σyr最大值均发生在次表面z/a0=0.36处。纯滚动和Qx=0.1P时,接触表面产生轴向残余拉应力,且2种工况下轴向残余应力随深度的分布曲线基本重合。Qx=0.3P和Qx=0.5P时,接触表面产生轴向残余压应力。
图10所示为循环载荷p0=4.21k作用10次后,切向力对残余剪切应变γxzr随深度分布的影响。可以看出,切向力Qx对残余剪切应变的影响较大。在接触表面附近,γxzr随切向力的增加以指数形式增长,与文献[15]分析结果趋势相似。当Qx/P大于等于0.3时,最大γxzr发生在接触表面,与文献[16]试验观察一致。当Qx/P=0时,次表面γxzr为负值,但相比其他3种工况,剪切应变很小。3种Qx/P非零工况,在当前坐标系下,残余剪切应变为负值。在4种Qx/P工况下,残余剪切应变均分布在z/a<1.1范围内,Qx/P对残余剪切应变深度分布范围影响较小。

3 结论
利用ABAQUS建立了车轮三维弹塑性有限元模型,模型中采用Lemaitre-Chaboche非线性各向同性随动硬化循环塑性模型,运用Hertz接触理论和全滑动切向理论来模拟轮轨反复滚动过程,通过有限元分析得到以下结论:
(1) 通过数值模拟得到了车轮接触表面附近的残余应力和残余应变随循环载荷的累积发展过程和随深度的分布规律。
(2) 纯滚动工况下最大接触压力越大,残余应力和残余应变越大,残余应力和残余应变最大值均发生在车轮次表面。
(3) 切向力对车轮接触表面附近的残余应力和残余应变影响显著,切向力作用下残余剪切应变最大值发生在滚动接触表面。
参考文献:
[1] 金学松,张继业,温泽峰,等. 轮轨滚动接触疲劳现象分析[J]. 机械强度, 2002, 24(2):250-257.
JIN Xuesong,ZHANG Jiye,WEN Zefeng,et al. Overview of Phenomena of chanical Strength,2002,24(2):250-257.
[2] 温泽峰,金学松. 非稳态纯滚动接触弹塑性分析[J]. 固体力学学报,2006,27(4):355-361.
WEN Zefeng,JIN Xuesong. Elastic-plastic Analysis of Non-steady State Pure Rolling Contact[J].Acta Mechanica Solida Sinica,2006,27(4):355-361.
[3] 温泽峰,金学松,肖新标.非稳态载荷对二维轮轨纯滚动接触应力和变形的影响[J].交通运输工程学报,2006,27(4):14-19.
WEN Zefeng, JIN Xuesong, XIAO Xinbiao. Influence of Non-steady State Loading on Two-dimensional Wheel-rail Pure Rolling Contact Stresses and Deformation[J]. Journal of Traffic and Transportation Engineering, 2006,27(4):14-19.
[4] 李伟,温泽峰,吴磊,等. 车轮滑动时钢轨热弹塑性有限元分析[J]. 机械工程学报,2010,46(10):95-101.
LI Wei, WEN Zefeng, WU Lei, et al.Thermo-elasto-plastic Finite Element Analysis of Rail During Wheel Sliding[J]. Journal of Mechanical Engineering, 2010, 46(10); 95-101.
[5] 郭俊,温泽峰,金学松,等.钢轨三维弹塑性滚动接触应力[J]. 西南交通大学学报,2007,42(3):262-268.
GUO Jun,WEN Zefeng,JIN Xuesong,et al. Three Dimensional Elastic-plastic Rolling Contact Stresses in Rail[J]. Journal of Southwest Jiao Tong University, 2007, 42(3):262-268.
[6] 张军,吴昌华.轮轨接触问题的弹塑性分析[J].铁道学报,2000, 22(3): 16-21.
ZHANG Jun, WU Changhua. Elasto-plastic Analysis of Wheel Rail Contact Problem[J]. Journal of the China Railway Society,2000,22(3): 16-21.
[7] 常崇义,王成国.基于ALE有限元的轮轨稳态滚动接触分析[J]. 中国铁道科学,2009,30(2):87-93.
CHANG Chongyi, WANG Chengguo.Wheel-rail Steady State Rolling Contact Analysis Based on ALE Finite Element Method[J]. China Railway Science, 2009,30(2):87-93.
[8] 肖乾,车宇翔,周新建,等.轮轨滚动接触棘轮效应数值分析[J].铁道学报,2013,35(12):19-23.
XIAO Qian, CHE Yuxiang, ZHOU Xinjian, et al. Numerical Analysis on Ratcheting Effect of Rolling Contact Between Wheel and Rail[J].Journal of the China Railway Society,2013,35(12):19-23.
[9] VERNERSSON T,CAPRIOLI S,KABO E, et al. Wheel Tread Damage: A Numerical Study of Railway Wheel Tread Plasticity Under Thermomechanical Loading[J]. Part F: J. Rail and Rapid Transit,2010,244(5):435-443.
[10] JOHNSON K L. Contact Mechanics[M]. Cambridge:Cambridge University Press,1985.
[11] 金学松,刘启跃.轮轨摩擦学[M].北京:中国铁道出版社,2004:51-57.
[12] LEMAITRE J, CHABOCHE J L. Mechanics of Solid Materials[M]. Cambridge:Cambridge University Press, 1990.
[13] EKH M, JOHANSSON A, THORBERNTSSON H, et al. Models For Cycilc Ratchetting Plasticity-Integration and Calibration[J].Journal of Engineering Materials and Technology,2000,122(6):49-55.
[14] RINGSBERG J W. Cyclic Ratchetting and Failure of a Pearlitic Steel[J]. Fatigue&Fracture of Engineering Materials & Structure,2000,23(15):747-758.
[15] JIANG Y Y , XU B,SEHITOGLU H . Three-dimensional Elastic-plastic Stress Analysis of Rolling Contact[J]. ASME Journal of Tribology,2002,124(4):699-708.
[16] SATOM, ANDERSON P M, ANDERSOND A. Rigney Rolling-sliding Behavior of Rail Steels[J]. Wear,1993,14(3): 159-172.
