基于仿真计算的25 m钢轨运输偏重问题研究
2016-05-08杨能普
韩 梅, 郑 航, 方 哲, 杨能普
(北京交通大学 交通运输学院, 北京 100044)
随着我国铁路事业快速发展,每年钢轨运输量十分巨大,其中长度为25 m的60 kg/m的钢轨(以下简称25 m钢轨)更是占很大比重。根据文献[1],运输该种钢轨主要采用六支点转向架跨装的运输方式,见图1,这种方式在实际运行中偏重问题十分突出。偏重是指装车后,车辆任一转向架所承受的货物重量超过货车容许载重量的1/2,或2个转向架承受重量之差大于100 kN[2]。当发生严重偏重时,将导致车辆一端车钩翘起,在线路变坡点发生脱钩现象,产生车辆溜逸,甚至造成列车冲突、撞车等事故。因此,研究25 m钢轨偏重问题对保证运输安全具有十分重要意义。
现有研究表明,车辆悬挂状态、车地板高度、支点数量及高度以及线路状态对25 m钢轨运输偏重情况均具有一定影响,可以通过使用四支点承载25 m钢轨、使用2支承货物转向架,以及开发25 m钢轨运输专用车等方式改善偏重现象,但这些方式都不能从根本上解决车辆偏重问题[3]。
目前常用的六支点转向架由2个高度为235 mm的货物转向架和4个高度为200 mm的滑台组成,在跨装车组上的放置位置见图1。图1中1~6分别为6个支点,其中:支点2、5为货物转向架,支点1、3、4、6为滑台。

本文运用力矩平衡与弯曲变形原理分析25 m钢轨6个支点及车辆转向架的受力,建立25 m钢轨实体模型并进行有限元仿真计算,通过改变六支点转向架的支点高度和支点纵向位置,研究确定25 m钢轨运输偏重问题的解决方案。
1 钢轨力学模型分析
1.1 货物支点承受重量计算原理
根据文献[1],25 m钢轨装载方案见图1,使用60 t木地板平车装载4层,梯形码放,共75根,总计质量105 kg。
首先对钢轨支点进行受力分析,将钢轨视作简支梁,由于有6个约束,其中4个多余约束,为静不定梁,静不定次数为4。假设支点2~支点5的约束为多余约束,设想将其约束解除,得到原静不定梁的静定基,再分别以约束反力F2、F3、F4、F5代替多余约束,则得到原静不定梁的相当系统,见图2。

为保证相当系统和原静不定梁具有相同的受力变形,在多余约束反力处的变形与原静不定梁在该处的变形应相同,以此可建立以下等式[4]为
( 1 )
( 2 )
( 3 )
( 4 )
式中:Lij为支点i与支点j距离(i、j=1,2,3,4,5,6且i≠j),m;Fi为支点i处约束反力(i=2,3,4,5),N;q为钢轨重力的等效均布载荷,N/m。
联立式( 1 )~式( 4 ),可求得F2、F3、F4、F5。令支点1、支点6处的约束反力为F1、F6。由力矩平衡可得
L12F2+L13F3+L14F4+L15F5+
L16F6-0.5L16G=0
( 5 )
式中:G为钢轨的重力,N。
由各支点力之和等于重力可得
F1+F2+F3+F4+F5+F6-G=0
( 6 )
联立式( 5 )、式( 6 )求得F1、F6。
1.2 车辆转向架承受重量计算原理
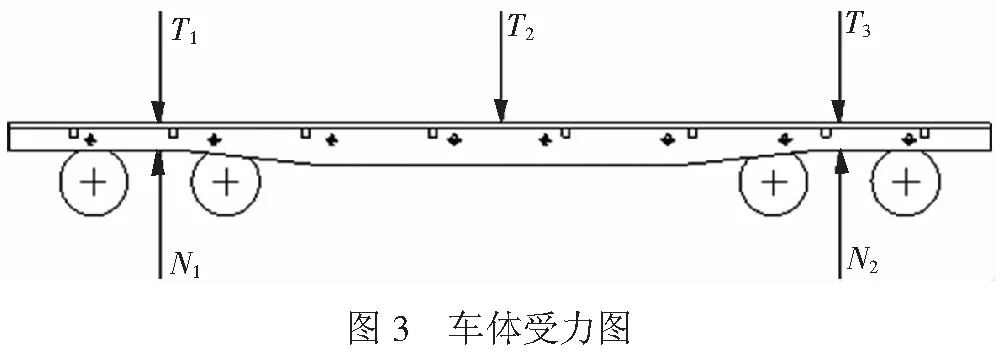
以1辆重车为例,分析车辆转向架承受货物重量的计算方法。假设六支点转向架在该重车上的3个支点对平车的作用力分别为T1、T2、T3,见图3,大小分别与F1、F2、F3相等;令车辆2个转向架承受的货物重量分别为N1、N2,则根据力矩平衡原理建立等式( 7 )、式( 8 ),由此得出车辆转向架承受货物重量大小,并以此判断车辆偏重与否。
T2×L12+T3×L13=N2×L13
( 7 )
T2×L23+T1×L13=N1×L13
( 8 )
由式( 7 )和式( 8 )可得
N1=(T1×L13+T2×L23)÷L13
( 9 )
N2=(T2×L12+T3×L13)÷L13
(10)
2 建立钢轨有限元模型
2.1 三维实体模型建立与网格划分
应用SolidWorks建立60 kg/m钢轨实体模型[5],见图4。
应用HyperMesh进行网格划分,采用的材料为钢,密度为7.8 g/cm3、弹性模量202 GPa、泊松比0.3。
考虑精度及计算速度,对钢轨截面进行网格划分[6],网格大小采用10 mm;对梁单元进行网格划分,网格大小采用150 mm,见图5。
2.2 约束条件及载荷设置
运用ANSYS计算各支点受力时,需设置相应的约束条件。图1的钢轨装载方案中, 支点2、支点5为货物转向架,对其进行全约束。支点1、3、4、6为滑台,对其进行垂向位移约束,以保证该支点的最大挠度值为货物转向架与滑台的高度差[7]。
添加载荷时,按竖直向下添加等同1个重力加速度下重力大小的均布载荷。
2.3 计算工况设置
图1中,定义支点1~支点3所在车辆为前车,支点4~支点6所在车辆为后车,车辆转向架也以此方向为前后。根据文献[1]的要求,装载钢轨的两车车地板高度之差不得大于20 mm。另外,运输过程中钢轨允许最大窜动量为150 mm。因此,工况设计中两车车地板高度差选用最大值20 mm,钢轨纵向位移选用最大值150 mm。综上,设计以下5种计算工况。
工况1:两车地板等高,钢轨无纵向位移;工况2:前车地板低20 mm,钢轨无纵向位移;工况3:两车地板等高,钢轨窜动向支点1方向纵向位移150 mm;工况4:前车地板低20 mm,钢轨向支点1方向纵向位移150 mm;工况5:前车地板低20 mm,钢轨向支点6方向纵向位移150 mm。
3 有限元计算结果分析
运用ANSYS进行有限元计算,结果见表1。
由表1可知,以上5种工况车辆转向架承担的货物重量差均小于100 kN,满足文献[8]要求,且有一定裕量;但后车的前转向架承担的货物重量始终大于车辆容许载重量的1/2(即300 kN),不满足文献[8]要求,故车辆均已发生偏重。
由此可以看出,目前25 m钢轨运输偏重的主要表现为车辆的1个转向架承担的货物重量超过车辆容许载重量的1/2,而非2个转向架承重差大于100 kN。其中在工况4下,后车前转向架承担的货物重量最大,为304.34 kN,故工况4为最不利工况。该计算结果与实际运输中经常产生偏重的情况相符。
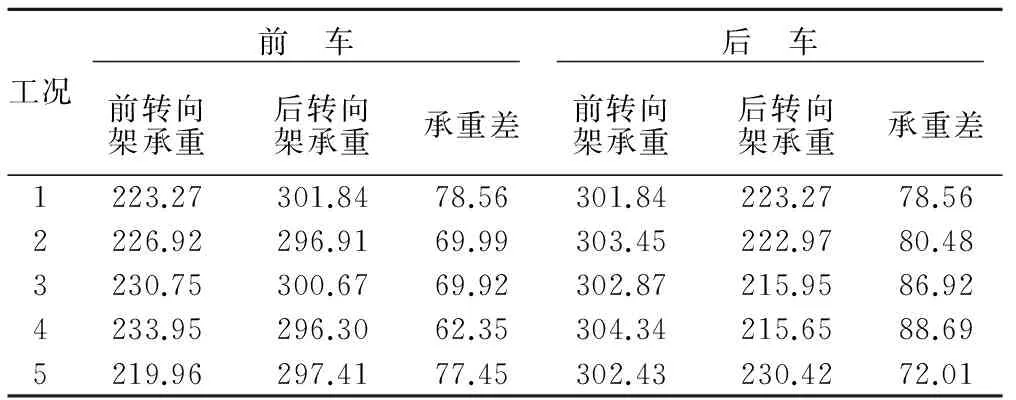
表1 转向架承重对比情况 kN
4 装载方案改进
为解决偏重问题,现研究改进的装载方案。本文提出改进方法为
(1) 改变支点高度;
(2) 改变支点在车辆的纵向位置。
根据前述分析可知,工况4为最不利工况。因此,将依据工况4对改进方案验算能否实现车辆转向架承受货物重量不大于300 kN,最终解决偏重问题。
4.1 改变支点高度的改进方案
现行方案中支点1、3、4、6高度为200 mm,支点2、5为235 m,改进方案按以下2种方式考虑
(1) 支点 1、6高度不变,改变支点3、4高度;
(2) 支点3、4高度不变,改变支点1、6高度。
支点1、6高度不变,支点3、4高度的变化与车辆转向架承受的最大货物重量关系见图6。由图6可看出,车辆转向架最大承重值随着支点3、4高度的降低而逐渐减小,但变化并不明显,且即使支点3、4高度降为0时,车辆转向架承重值仍大于300 kN,故改变支点3、4高度并不能解决偏重问题。支点3、4高度不变,支点1、6高度的变化与车辆转向架承受的最大货物重量关系见图7。

由图7可看出,车辆转向架最大承重值随着支点1、6高度的增加而逐渐减小,但变化不十分明显,且当支点1、6高度达到405 mm时,车辆转向架承重值仍大于300 kN。根据实际情况,部分支点高度过高可能对钢轨造成一定的损伤,且影响运输稳定性及安全性,故改变支点1、6高度也不能解决偏重问题。
综上可得,改变支点高度并不能解决偏重问题。
4.2 改变支点纵向位置的改进方案
改变支点在车辆上的纵向位置时,做以下定义:(1) 将支点向靠近2个车辆中间方向移动称为内移;(2) 将支点向远离2个车辆中间方向移动称外移;(3) 支点外移方向为正,内移方向为负;(4)x为支点1、6外移量,y为支点3、4外移量;(5)z为跨装车组的4个转向架中承受货物重量的最大值。
为综合分析支点在车辆上的纵向位置变化对车辆转向架承担货物重量的影响,现同时改变支点1、6和支点3、4的纵向位置,计算得出支点1、6和支点3、4在不同纵向位置时车辆转向架承重量的最大值,即当x和y取不同值时,计算出相应的z值。其中x的取值范围为[-1 350 mm,600 mm],y的取值范围为[-600 mm,900 mm],当x和y的取值超出该范围时将出现某些支点不受力的情况,将使其余支点承受重量过大,不利于车辆运行安全。
应用ANSYS计算出不同x和y值下对应的z值,再将计算结果运用MATLAB进行拟合,得出z关于x和y的二元函数曲面,见图8。
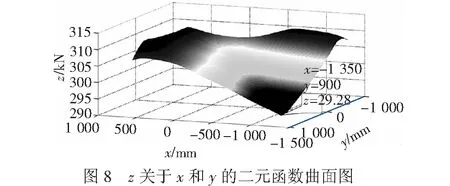
由图8可知,当x为-1 350 mm、y为900 mm时,z达到最小值292.8 kN,此时z值小于300 kN,即表明偏重问题得到解决。
由以上分析计算可得出,25 m钢轨运输偏重问题的解决方案为将支点1、6分别内移1 350 mm,将支点3、4分别外移900 mm。
4.3 改进方案在其它工况下的验算
下面对前文确定的改进方案在其它工况下车辆转向架承担货物重量进行计算,验算是否满足文献[8]要求,计算结果见表2。
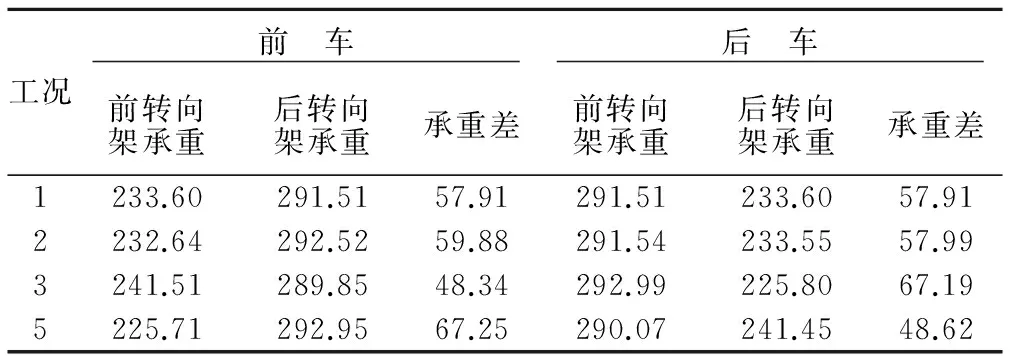
表2 改进方案在其它工况下的转向架承重 kN
由表2可知,在其它4种工况下,车辆转向架承担货物重量均小于300 kN,最大值为292.99 kN,满足文献[8]要求。与表1对比可知,采用改进方案时,车辆2个转向架承重差有所降低,安全性更好,故该方案可行。
4.4 最终方案确定
通过前文分析,最终得出可行的改进方案为在现行装载方案基础上将支点1、6向跨装车组内方移动1 350 mm,将支点3、4向跨装车组外方移动900 mm。若以跨装车辆最左端为坐标原点,可得出各支点坐标和高度,见表3。
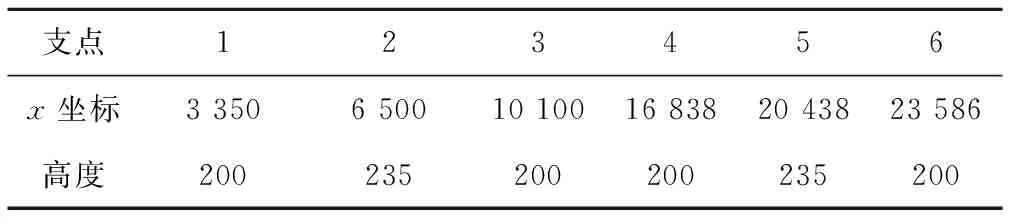
表3 最终方案支点坐标、高度值 mm
5 结束语
本文分析、计算采用六支点转向架运输25 m钢轨偏重问题,提出改变支点高度和纵向位置2种改进方案。计算结果表明,将支点1、6向跨装车组内方移动1 350 mm,将支点3、4向跨装车组外方移动900 mm的改进方案能够解决偏重问题,对完善我国铁路25 m钢轨装载方案具有一定的指导意义。
本文的研究结果是基于仿真分析与计算得出的,其应用效果还需通过实际试验进行实测验证。
参考文献:
[1] 中华人民共和国铁道部.铁路货物装载加固定型方案[M].北京:中国铁道出版社,2010:150-155.
[2] 韩梅.铁路货运技术[M].北京:北京交通大学出版社,2013:15-17.
[3] 赵勇,张中平.关于使用六支点货物转向架跨装25 m钢轨偏重问题的探讨[J].铁道货运,2011,29(1):35-37.
ZHAO Yong, ZHANG Zhongping. Discussion on Unbalanced Weight Problem of Using 25 m Rail Six-fulcrum Freight Turing Rack[J]. Railway Freight,2011,29(1):35-37.
[4] 祝瑛,蒋永莉.工程力学[M].北京:北京交通大学出版社,2010:32-34.
[5] 赵罘,秦志峰,王宇飞. SolidWorks 2013从入门到精通(中文版)[M].北京:兵器工业出版社,2013:98-101.
[6] 周传月.HyperMesh从入门到精通[M].北京:科学出版社,2005:74-76.
[7] 丁源,吴继华.ANSYS CFX 14.0从入门到精通[M].北京:清华大学出版社,2013:154-157.
[8] 中华人民共和国铁道部.铁路货物装载加固规则[M].北京:中国铁道出版社,2012:3.
