基于测录井信息的泥页岩渗透率优化计算方法

闫建平, 温丹妮, 司马立强, 温新房, 耿斌, 李尊芝, 言语

(1.西南石油大学天然气地质四川省重点实验室, 四川 成都 610500; 2.西南石油大学地球科学与技术学院, 四川 成都 610500; 3.江苏油田勘探局地质测井处, 江苏 扬州 225002;4.中石化胜利油田分公司地质科学研究院, 山东 东营 257015)

0 引 言

页岩油气是重要的非常规油气资源,北美德克萨斯州Barnett页岩的成功开发催化了全球页岩油气勘探开发热潮[1]。目前,页岩(泥页岩)油气储层也成为中国非常规油气备受关注的勘探目标。苏北盆地古生界到新生界地层中发育多套优质生烃泥页岩层系[2-3],分布区域广泛,其中,盐城凹陷的阜二段页岩中见到良好的油气显示[4],G凹陷在阜二段、阜四段也获得工业油流,表明苏北盆地页岩层系中具有形成页岩油气的良好成烃、成藏条件和资源潜力。通常,页岩油气具有连续成藏特点[5],脆性矿物含量较高、裂隙发育的有利页岩储层识别及评价是有效开发页岩油气的关键。测井资料具有成本低、纵向连续性好、地质信息丰富等优点[6],对成熟的勘探区进行测井地球化学和储层评价是目前页岩油气勘探较为理想的思路和方法[7],但页岩是典型的致密多孔介质,孔隙度和渗透率极低,孔隙尺寸主要分布在5～800 nm[8],传统的达西定律不再适用于致密性页岩油气藏[9]。页岩油气藏由于其孔隙结构的致密性和复杂性,常规试验方法无法准确测量页岩的渗透率和孔隙度[10],且裂隙存在使得泥页岩渗透率准确计算难度更大。

以苏北盆地G凹陷阜宁组泥页岩地层为研究对象,采用常规K—φ模型、变指数Timur经验模型等计算的渗透率误差都较大,不能满足泥页岩储层评价的要求,分析主要因素是裂隙存在使得渗透率明显改善,常规方法不能有效计算裂隙渗透率。分析泥页岩发育裂隙的测录井响应特征,发现泥页岩储层发育裂隙时一般多数为脆性矿物含量高的灰质岩相,借鉴敏感测录井变量可识别泥页岩剖面中发育裂隙的层段,以此为基础,分有、无裂隙建立渗透率模型,精度有明显提高。最后,鉴于裂隙发育层段往往灰质含量高、GR值低,裂隙渗透率与GR值有明显的负相关关系,由此提出利用GR对裂隙渗透率进行修正,得到渗透率优化计算公式,在GR曲线高分辨率处理后,利用该方法计算渗透率效果较好,尤其是提高了裂隙渗透率的计算精度,为精确计算泥页岩储层物性参数奠定了基础。

1 泥页岩裂隙对渗透率的影响

塑性相对较大的泥页岩储层在裂缝类型与成因、裂缝识别方法、裂缝参数估算等方面既有共性也有其特殊性[11],泥页岩储集空间通常是由微孔隙和裂隙(裂缝)共同构成[12],基岩渗透率、孔隙度很低,一般是良好的烃源岩和盖层,裂隙的存在对泥页岩的储集性、渗透性改善有较大的意义。

裂缝是泥页岩储层产能的主控因素之一,对页岩油气(藏)具有双重作用,裂缝系统既是油气的主要储存空间,也是渗流的主要通道,有助于页岩总含油气量的增加[13]。研究区物性分析资料表明,存在裂隙的样品渗透率明显较高,一般都大于10 mD*非法定计量单位,1 mD=9.87×10-4 μm2,下同,而非裂隙样品渗透率较低,不超过10 mD。从岩心孔隙度渗透率关系(φc-Kc)(见图1)可以看出,泥页岩地层具有双重孔隙介质特点,基岩表现为低孔隙度、特低渗透率特征,而发育裂隙(裂缝)对改善泥页岩地层的渗透性及储集性起了重要的作用。此外,岩心观察显示,多数裂缝发育的层段或裂缝面中往往显示含油、油迹,与含油性也有较好的关系。

图1 泥页岩有、无裂隙岩心孔隙度渗透率关系

2 泥页岩常规渗透率模型

2.1 孔隙度渗透率拟合关系

根据岩心孔隙度和渗透率的关系,建立渗透率模型(见图2)K=0.1533 e0.3694 φ。对模型进行45°线检验(见图3),发现当K>10 mD时,计算结果偏小;K<10 mD时计算偏大,计算精度较低。

图2 渗透率—孔隙度回归模型

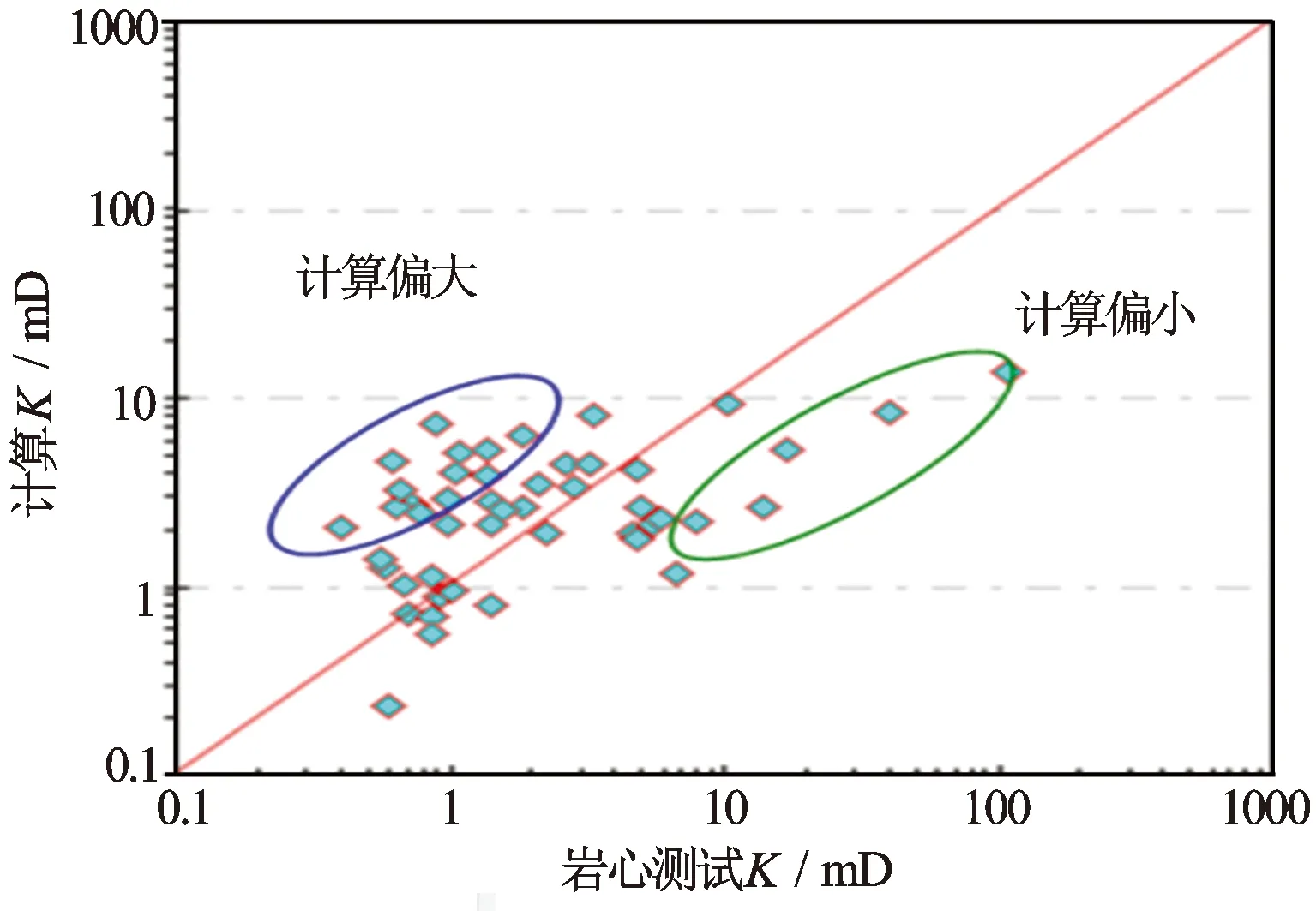
图3 K—φ模型检验

2.2 变指数Timur模型

计算渗透率常用的Timur公式[14]在砂泥岩地层应用效果较好,经过和岩心实验数据对比,要将其应用于泥页岩地层,需要分有、无裂隙而改变孔隙度指数,改变后的Timur公式

(有裂隙)

(1)

(2)

式中,K为渗透率,mD;Swb为束缚水饱和度,%;φ为密度孔隙度,%。

通过对A井的处理,用Timur模型检验(见图4),看出计算的渗透率与岩心分析数据离散性强,说明运用该方法计算渗透率效果也较差。

图4 变指数Timur模型检验

3 泥页岩渗透率优化计算

上述模型计算泥页岩地层渗透率不准确的主要原因是没有充分考虑裂隙(裂缝)对渗透率的影响,按双重孔隙介质理论,应该分基质、裂缝分别建立渗透率模型,准确有效地识别泥页岩裂隙层段。

3.1 泥页岩发育裂隙测录井响应特征

苏北盆地泥页岩地层压力系数主要为1.01～1.18(以A井阜四段为例),基本为常压地层,另外泥页岩物性较低(孔隙度一般低于10%,渗透率一般低于1.0 mD),因此,地层因素对气测影响较小,气测资料适用性较好。

钻时录井主要记录钻时曲线(Δtc,min/m),在钻井措施条件不变的情况下,影响钻时的主要因素是岩石性质(岩石可钻性)。A井岩心及测试资料显示的泥页岩储层段3 161.57～3 161.77 m(见图5),岩性为深灰色油浸含灰页岩,岩心显示有高角度裂缝,钻时及气测曲线特征为Δtc较低、全烃含量(THC,%)值非常高。测井曲线特征为声波时差值低、中子孔隙度值低、密度值高、GR低值、铀低、无铀伽马低、电阻率值高,发育裂隙储层段的测录井响应明显不同于非泥页岩储层段。通过分析,得到了发育裂隙的泥页岩储层识别模式:录井显示高Δtc背景中的低Δtc段,THC高;测井特征为AC低、CNL低、DEN高,GR相对低值。

图5 A井发育裂隙泥页岩储层段测录井响应特征*非法定计量单位,1 ft=12 in=0.304 8 m,下同

3.2 发育裂隙泥页岩储层地层模型

通过泥页岩储层测录井响应特征及适用性分析,发现泥页岩储层多为脆性矿物含量高的灰质岩相(发育裂隙),地层模型为泥岩(含灰泥岩)-灰质泥岩(灰质页岩)-泥岩(含灰泥岩)[见图6(a)]。发育裂隙的灰质泥岩(灰质页岩)全烃含量显示高值,这种全烃含量高的层位往往是高Δtc层位中的低钻时小层(钻时往往大于40 min/m,但一般不超过200 min/m),该泥页岩储层类型占多数。储层上下是富含有机质泥页岩相,GR值较高,富含有机质泥岩成熟演化过程中生成的烃大部分排入到有裂隙储集空间的灰质岩相中。

图6 泥页岩储层解释模型

另外,还有少数全烃含量高的泥页岩储层为脆性矿物含量较低的含灰页岩相,地层模型为含灰页岩—含灰(灰质)泥岩[图见6(b)],含灰页岩发育页理缝。这种全烃含量高的层位特征为:低Δtc层位中的高THC层段,往往黏土矿物含量较高,富含有机质泥页岩生成的烃大部分滞留在内部的微裂隙、微孔隙中,该泥页岩储层类型占少数。

3.3 裂隙泥页岩储层识别方法

鉴于这2种泥页岩储层发育的地层类型,提出相应解释泥页岩油气富集的2种解释模型。利用对泥页岩储层敏感的测录井信息GR、DEN、Δtc参数,建立了相应的识别图版GR—DEN—Δtc(半径)气泡图版(见图7),区分效果较好,解释模型1的DEN值通常大于2.50 g/cm3,GR值小于60 API,Δtc通常大于80 min/m,一般小于200 min/m(致密含灰或灰质泥岩Δtc往往大于200 min/m);而解释模型2的DEN值通常小于2.35 g/cm3,GR值通常大于70 API,Δtc小于40 min/m。

图7 GR—DEN—Δtc(半径)气泡图版

进一步采用AC、DEN、GR、Rt、Δtc、THC等6种变量建立雷达图版,能够更好地识别裂隙含油层(模型1)、泥岩含油层(模型2),具有较好的适用性(见图8)。

通过对×井的雷达图分析,得出,①泥岩裂缝含油层(模型1)全烃含量高、钻时高、自然伽马较低,电阻率偏低;②泥页岩含油层(模型2)全烃含量高、钻时低于模型1的值、自然伽马高值、电阻率整体偏低。

3.4 分基质、裂隙的渗透率模型

考虑到裂隙样品对渗透率的影响,试图分无裂隙、有裂隙样品分别建立各自的K—φ模型(见图9)。

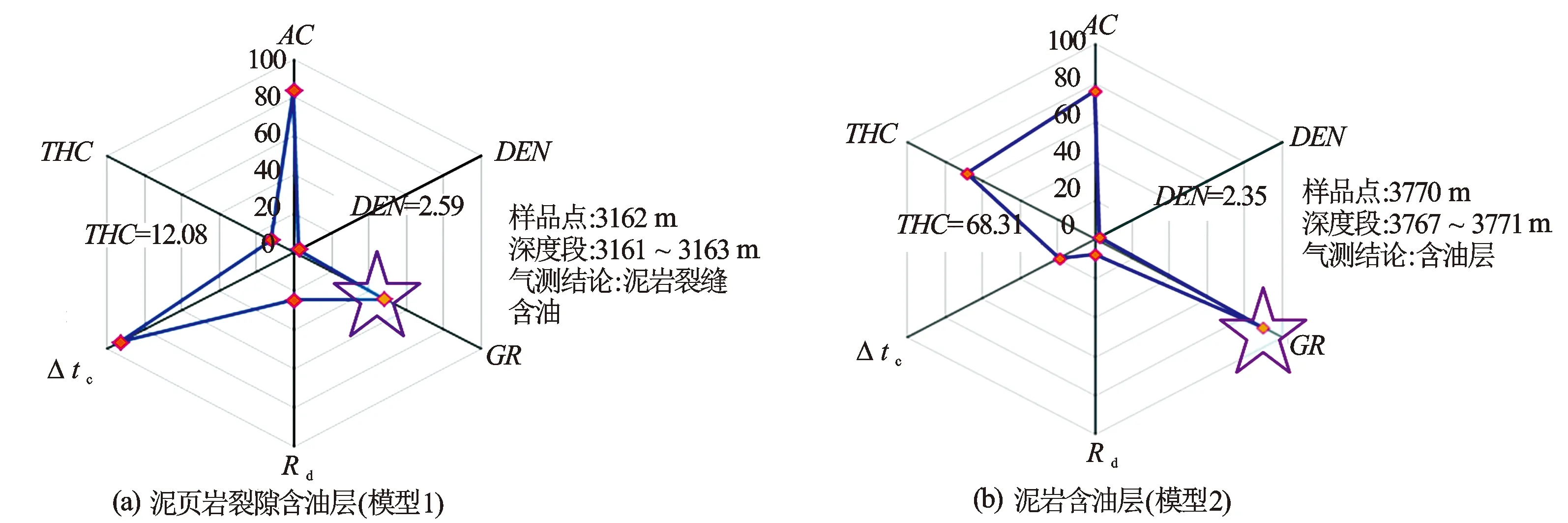
图8 ×井雷达图识别图版

图9 分有、无裂隙样品的K—φ模型

实际处理时,依据建立的发育裂隙泥页岩储层解释模型,可较好地识别地层剖面中发育裂隙的层段。裂隙层段特征表现为钻时曲线高层段中的相对低钻时小层,且全烃含量高(占多数),往往对应灰质泥页岩相,GR较低、AC较低。在裂隙泥页岩储层识别的基础上,再采用有、无裂隙的K—φ模型进行计算,对模型进行45°线检验,精度较统一的K—φ模型、变指数Timur模型有明显的改善。但45°线检验图是对数坐标,表明裂隙渗透率计算仍然存在个别计算点数量级的误差,这是由于本身裂隙渗透率模型的误差引起,对于高裂隙渗透率值仍然需要进行优化计算。

3.5 裂隙渗透率模型优化计算

裂隙主要出现在泥页岩地层模型1中,由于岩石致密、脆性矿物含量高、泥质及有机质含量较少,往往自然伽马值较低。因此,鉴于裂隙往往发育于低自然伽马值的层段,分析裂隙渗透率与自然伽马值之间的关系,二者相关性很好(见图10),提出利用自然伽马值对裂隙渗透率进行校正。设自然伽马校正的裂隙渗透率函数关系为

K=af(φ)+bf(GR)

(3)

通过拟合得到系数a=0.007、b=1.001,进一步得到裂隙渗透率优化计算公式

K=0.03451 e0.1634 φ+2.002×1016GR-0.8117

(4)

图10 裂隙渗透率与GR值关系

考虑到泥页岩薄互层特性,自然伽马测井分辨率往往不能较好地反映泥页岩薄互层界面,有必要进行自然伽马曲线高分辨率处理。从信号分析角度,可将测井曲线抽象为仪器探测范围内地层综合响应信号的叠加,某一深度点的自然伽马测井值并不是该点的真实测量响应值,而是测点及其围岩测量值的加权平均值,通过对测井曲线进行反褶积处理[15],得到了高分辨率自然伽马曲线GRR(见图11),可提高对泥页岩薄层界面的识别能力。

图11 A井渗透率处理结果对比

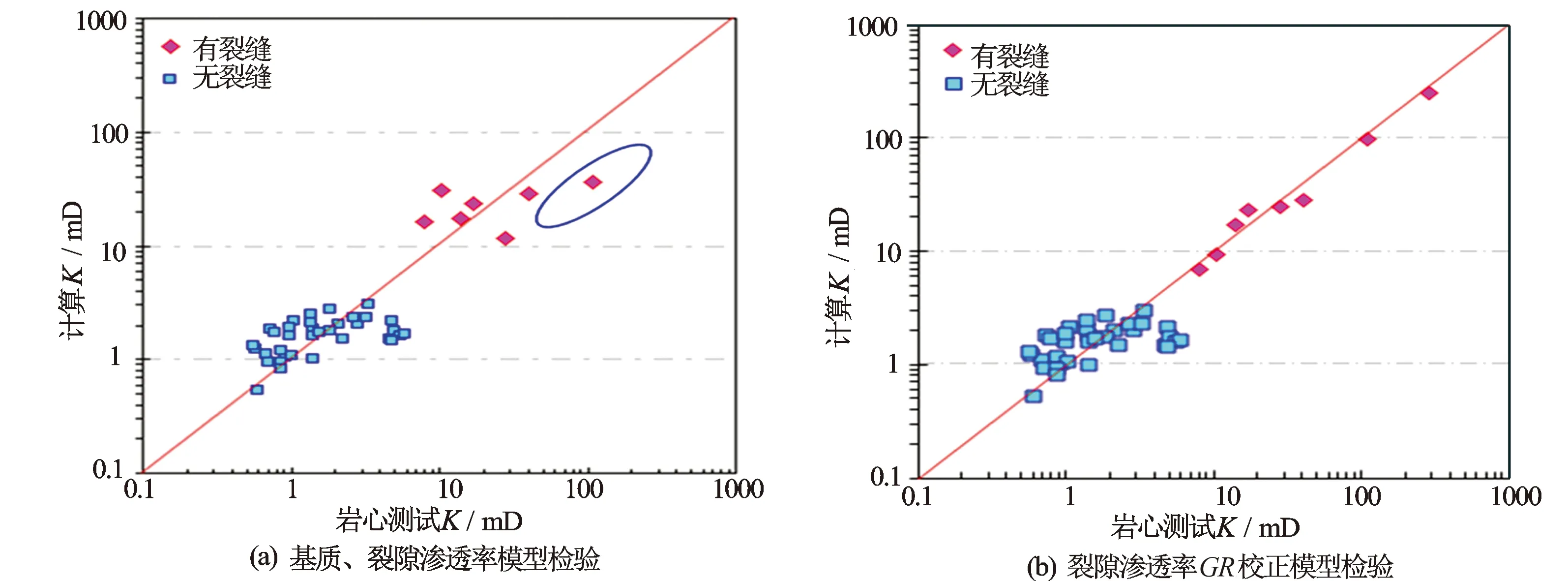
图12 泥页岩渗透率模型优化计算检验

进一步,将高分辨率自然伽马曲线GRR带入式(4)进行计算,结果表明该优化方法计算渗透率效果较好,尤其是提高了有裂隙的渗透率计算精度[见图12(b)],为泥页岩储层物性参数准确计算奠定了基础。

4 结 论

(1) 采用统一的孔隙度渗透率关系、变指数Timur模型等计算渗透率误差较大,不能满足泥页岩储层评价的要求,主要原因是常规的方法不能有效计算裂隙渗透率。

(2) 泥页岩发育裂隙多数为脆性矿物含量高的灰质岩相,将测录井响应结合,可较好地识别泥页岩中裂隙层段,分有、无裂隙分别建立渗透率模型,计算结果有明显改进。

(3) 鉴于裂隙往往发育于黏土矿物少、自然伽马值低的层段,提出利用自然伽马值对渗透率进行校正,得到渗透率优化计算公式,在进行自然伽马曲线高分辨率处理的基础上有效提高了裂隙渗透率计算精度。

参考文献:

[1] Chuck Boyer, Bill Clark, Valerie Jochen, et al. 全球页岩气资源概况 [J]. 油田新技术, 2011, 23(3): 28-39.

[2] 刘小平, 潘继平, 刘东鹰, 等. 苏北地区下寒武统幕府山组页岩气勘探前景 [J]. 成都理工大学学报: 自然科学版, 2012, 39(2): 198-205.

[3] 章亚, 刘小平, 董清源, 等. 苏北地区上二叠统龙潭组页岩气形成条件及有利区预测 [J]. 石油天然气学报, 2013, 35(3): 36-40.

[4] 郑开富, 彭霞玲. 苏北盆地上白垩统——第三系页岩油气成藏层位及有利区带 [J]. 地质学刊, 2013, 37(1): 147-154.

[5] Curtis J B. Fractured Shale Gas System [J]. AAPG (American Association of Petroleum Geologists) Bulletin, 2002, 86(11): 1921-1938.

[6] 闫建平, 蔡进功, 赵铭海, 等. 运用测井信息研究烃源岩进展及其资源评价意义 [J]. 地球物理学进展, 2009, 24(1): 270-279.

[7] 朱定伟, 王香增, 丁文龙, 等. 测井资料在优质页岩气储层识别中的应用——以鄂尔多斯盆地东南部长7段黑色页岩为例 [J]. 西安石油大学学报: 自然科学版, 2013, 28(2): 25-29, 34.

[8] 孙海, 姚军, 张磊, 等. 基于孔隙结构的页岩渗透率计算方法 [J]. 中国石油大学学报: 自然科学版, 2014, 38(2): 92-98.

[9] Javadpour F. Nanopores and Apparent Permeability of Gas Flow in Mudrocks (Shale and Siltstone) [J]. Journal of Canadian Petroleum Technology, 2009, 48(8): 16-21.

[10] Cui X, Bustin A M M, Bustin R M. Measurements of Gas Permeability and Diffusivity of Tight Reservoir Rocks: Different Approaches and Their Applications [J]. Geofluids, 2009(9): 208-223.

[11] 丁文龙, 许长春, 久凯, 等. 泥页岩裂缝研究进展 [J]. 地球科学进展, 2011, 26(2): 135-144.

[12] Pollastro R M, Jarvie D M, Hill R, et al. Geologic Framework of the Missipian Barnett Shale, Barnett-Paleozoic Total Petroleum System, Bend Arch-Fort Worth Basin, Texas [J]. AAPG Bulletin, 2007, 91(4): 405-436.

[13] 杨迪, 刘树根, 单钰铭, 等. 四川盆地东南部习水地区上奥陶统——下志留统泥页岩裂缝发育特征 [J]. 成都理工大学学报: 自然科学版, 2013, 40(5): 544-553.

[14] 孙建孟, 闫国亮. 渗透率模型研究进展 [J]. 测井技术, 2012, 36(4): 329-335.

[15] 张涛, 林承焰, 张宪国. 利用测井曲线反褶积方法提高薄层识别能力 [J]. 石油勘探与开发, 2010, 37(5): 579-582.