定向井轨迹误差模型研究

孟照魁, 焦焕静, 高爽, 白琳

(北京航空航天大学光电技术研究所, 北京 100191)

0 引 言

在井眼轨迹测量过程中存在诸多影响其精度的因素,这些误差源以不同方式影响测量值,导致井眼测量结果不精确,如果对每种误差源都进行校正和计算反而得不到真实的井眼轨迹不确定性范围。建立误差模型的目的是综合考虑各种导致测点数据出现误差的物理因素,最终确定在某一测量点处的位置误差范围。Wolff和De Wardt[1]于1981年发表了轨迹系统误差模型(WdW模型),该模型一经发表便成为工业标准。董本京等[2]总结出该模型存在多种缺陷,不适用现代仪器。1999年,Hugh Williamson[3]在SPE年度技术大会上提出随钻测量井眼不确定性模型。随后,该模型不断更新并在随钻测量领域得到广泛应用,但不完全适用于定向井分析过程[4-5]。

本文按测量误差在测点间的传播特性分为随机性误差或系统性误差,针对测斜仪测井过程中存在的测量误差提出其测量不确定度的误差模型,最后将该模型在Matlab中实现,通过实测数据可计算测量点在一定概率下的空间分布情况。

1 误差分析

结合测斜仪工作环境特性,在测量井眼轨迹过程中可能存在4种测量误差源[1-5]。

(1) 深度误差。一般情况下,若以电缆(或钢丝绳)方式计量,则深度误差为0.2×10-3,若监督不当,将会增加到1.5×10-3[6]。深度误差可分为4类独立误差项:随机性参考误差、系统性参考误差、刻度误差、拉伸误差。

(2) 偏心误差。使用、加工和安装精度导致仪器井下探管、耐压壳和井眼轨迹轴线有很大的偏差,引起井下仪器安装轴向偏离误差[7]。连续测斜仪的偏心误差分成4类独立误差项。

(3) 惯性器件安装误差。测斜仪的核心部分IMU由陀螺仪和加速度计组成,存在传感器安装不正交或仪器轴线方向不同轴等问题。这类传感器残余误差不可消除,在计算轨迹不确定性范围时必须考虑。

(4) 仪器精度误差。每种测斜仪都有自己的测量精度范围。本文以实验室研制的某测斜仪为例,该仪器井斜误差Δα=±0.2°,方位角误差为Δφ=±2.0°,这里方位角误差和井斜误差分为2类误差来考虑。

假设测量误差为随机性系统误差,各误差源相互独立,误差均值为0[8]。上述11项误差源均属于随机性系统误差,根据其在测点间的传播特性又可细分为系统性传播误差和随机性传播误差。相应的处理方法是对系统性传播误差进行代数和积累,对随机性传播误差进行均方和积累,应用中心极限定理确定井底位置的不定性范围[9]。

2 误差模型推导

井眼轨迹测量的典型过程是在被测井眼的一系列测量点上,仪器的惯性器件敏感各轴向上的测量参数分量,并采用航迹推算等算法解算出仪器在当前测量位置的姿态信息(井斜角I和方位角A),结合电缆测得的井深D,构成一个三维测量向量集,以此表述测点位置的井眼轨迹参数。仪器制造及测量工艺等原因,这些测量参数势必包含上文中所述11项测量误差。本文将误差精度指导委员会(ISCWSA)公布的随钻测量模型进行优化并应用到定向井测量领域,并根据误差源对测量参数的作用建模。

2.1 测点k处的误差向量

由于误差源i的存在,误差对某中间测点k处的作用为对前一测段和后一测段作用之和,其误差向量为式(1)。误差的累加在测量点终止,在该点的误差向量如式(2)所示,表明测量误差对该点的影响仅限于前一测段内。用σi,l表示第l个测段内第i项误差源的误差量级。∂pk/∂εi为该项误差的权重函数,表示考虑了单个测量误差可能会受实际井斜角、方位角和测量时间影响。dΔrj/dpk表示井眼位置向量对误差源的导数。

(1)

(2)

使用平衡正切曲线计算模型可将Δrk表示成式(3)[3]。将该式求微分可得出式(4)。

(j=k,k+1)

(3)

(j=k,k+1)

(4)

2.2 测点k处误差项累加

在测量点处的位置不确定性矩阵由误差向量累加获得,上述4种11项误差用数学式表示的误差源累积分为2种情形。

(1) 误差项i为随机误差源。在测段l中(不包括计算终点),某随机传播误差源i对测点不确定性影响为

(5)

所有测段内总的贡献为

(6)

(2) 误差项i为系统误差源。对于具有系统传播特性的误差源i,在测段l中,对测点位置不确定性的贡献为

(7)

所有测段内总贡献为

(8)

各误差源累加,得到总的位置协方差阵为

(9)

其中,上标svy表示在测点处的不确定性。

2.3 转换到井眼参考坐标系

以上推导出的公式都是基于当地地理参考坐标系(北,东,天,下标为nev)。协方差矩阵需要转换到更直观的井眼参考坐标系(高边,侧边,沿井眼方向,下标为hla)中才方便分析。M为转换矩阵,其转换方法为[10]

Chla=MTCn evM

(10)

根据正态分布,井眼位置误差的分布概率密度为

(11)

Δrg为考虑误差后的井底位置向量增量。其等概率密度面为

(k为常数)

(12)

因为Chla为实对称矩阵,根据线性代数,可得误差椭球方程为

(13)

设椭球族主轴为OU,OV,OW。该式为误差椭球方程,其半轴长平方分别为a2=k2λ1,b2=k2λ2,c2=k2λ3。k为放大系数,可根据给定的概率确定。式(13)表明,轨迹上各点是在以轨迹计算点为中心的,由相关矩阵及概率两者共同决定的散布范围——误差椭圆(球),并且可用此模型对各误差的实际数值进行评估。图1显示2种坐标系椭球形态。

3 仿真分析

3.1 仿真数据

以任91井的上测过程部分数据为例,截取部分的测深范围为445～2 605 m,因所用测斜仪为连测模式,测斜数据实时更新,为避免数据处理的冗杂,每5 m选取1个测点。该组数据先用实验室所研制的测斜数据处理软件处理多处粗差,以求实验数据真实可靠,提高计算结果的有效性。

3.2 仿真流程及环境

井眼轨迹不确定性分析的过程中,判断第i项误差源传播模式是否为系统性传播显得相当重要。将上述误差模型的算法在Matlab平台下编制代码,仿真流程按照图2所示步骤执行。

图2 模型仿真流程图

3.3 仿真结果分析

仿真所取放大因子为2,表明产生一个概率为73.9%的误差椭球,即井眼轨迹落在一个以测点为中心、轴半径为a,b,c的椭球内的概率为73.9%。对于测点处误差椭球在hla坐标系下的3个半轴长度,实验数据结果如图3至图5所示。表1截取了图3～图5中100 m范围内的数据作分析。

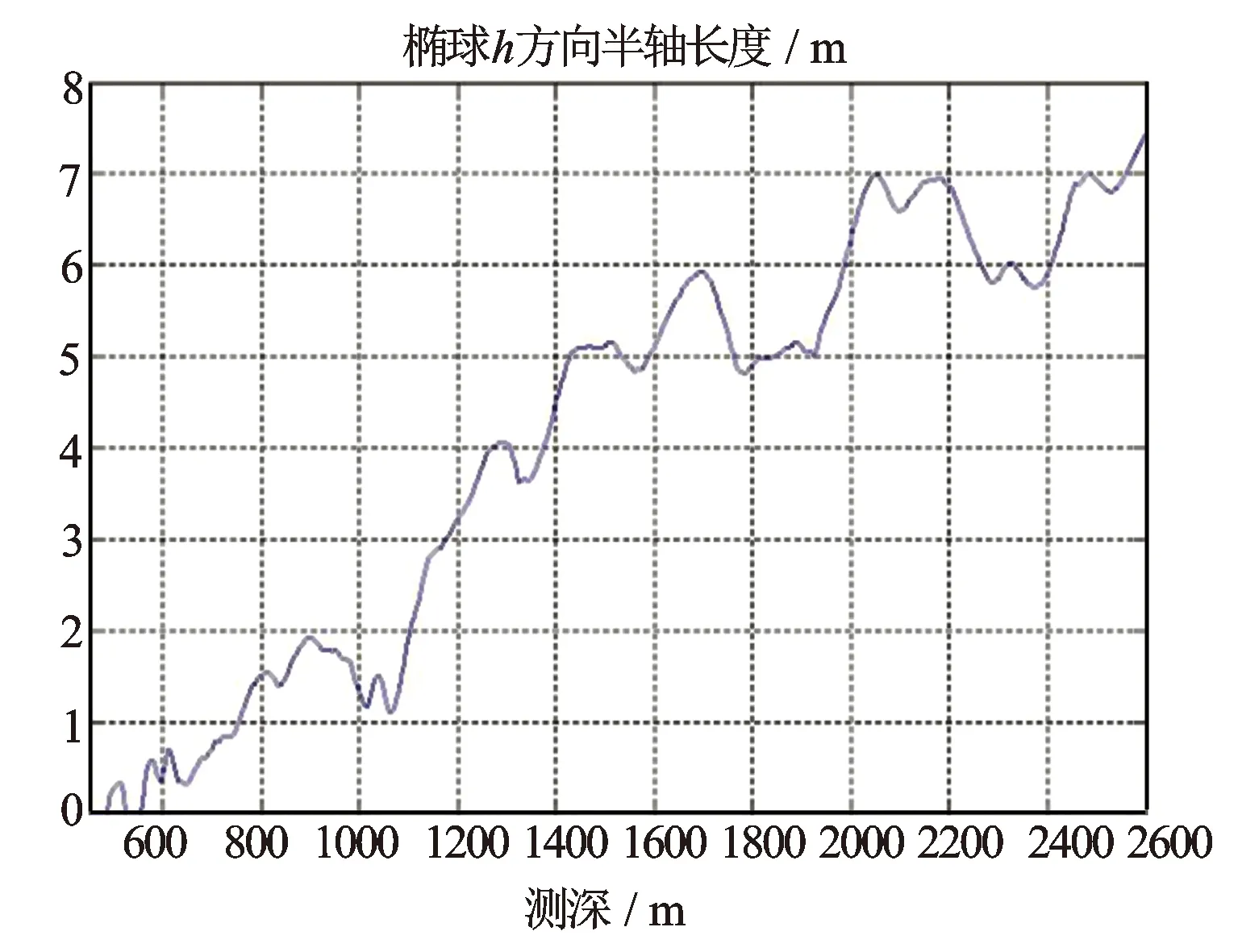
图3 椭球长半轴长度变化趋势图

根据井眼数据计算结果(见表1),结合仿真分析结果图可得出2点结论:①测点间误差是逐渐累积的趋势,3个方向上的半轴长度都随着测深的增加而呈增长趋势,符合测量误差传播的一般规律;②用该模型确定的是一系列以测点为中心,概率为73.9%的误差椭球。

图4 椭球短半轴长度变化趋势图

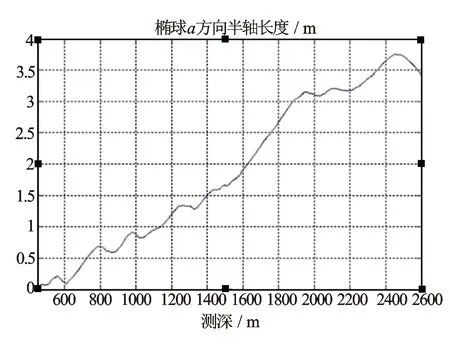
图5 椭球井眼方向半径长度变化趋势图

表1 井眼部分数据计算结果表

4 结 论

(1) 影响测斜仪测量误差的原因不容忽视,以ISCWSA协会提供的随钻测量模型为依据,本文结合实际油田数据,选定定向井测量过程可能存在的几类误差项,进行误差分析建模,最终得出一系列以测点为中心,概率为73.9%的误差椭球。

(2) 误差椭球在没有指定置信水平的情况下是没有定量意义的,当概率变化时,得出椭球的半径也会不同。

(3) 井眼坐标3个方向上的半轴长度都随着测深的增加而呈增长趋势,符合测量误差传播的一般规律,可有效地为测斜数据解释部门提供更科学的测斜数据,为促进救险井相交和丛式井防碰提供可靠依据。

参考文献:

[1] Chris J M Wolff, John P De Wardt. Borehole Position Uncertainty——Analysis of Measuring Methods and Derivation of Systematic Error Model [J]. SPE 9223, 1980: 1-7.

[2] 董本京, 高德利, 柳贡慧. 井眼轨迹不确定性分析方法的探讨 [J]. 天然气工业, 1999, 19(4): 59-63.

[3] Williamson H S. Accuracy Prediction for Directional Measurement While Drilling [J]. SPE67616, 2000: 221-233.

[4] 马劲松. 定向井随钻测量新模型误差源分析 [J]. 科技专论, 2014(13): 325.

[5] 麦埃尔, 欣尼G A, 伊尔费尔德H M J. 用于地下井的相对和绝对误差模型: 中国, CN 102356212 A [P]. 2012-02-15.

[6] 陈伟卿. 定向井轨迹误差分析及三维可视化描述研究 [D]. 北京: 中国石油大学, 2006.

[7] 许昊东, 黄根芦, 韦红术. 改进仪器不对中误差的轨迹系统误差模型研究 [J]. 科学技术与工程, 2013, 13(31): 9180-9183.

[8] 何辛. 用WdW模型估算定向井轨迹误差 [J]. 钻采工艺, 1989, 12(2): 23-28.

[9] Angus Jamieson. Introduction to Wellbore Positioning [M]. Inverness: The Research Office of UHI, 2012.

[10] 柳贡慧, 董本京, 高德利. 误差椭球(圆)及井眼交碰概率分析 [J]. 钻采工艺, 2000, 23(3): 5-12.