求解泄漏Lamb波频散及衰减曲线的计算方法

杨旭辉, 余厚全, 陈强, 程峰

(长江大学, 湖北 荆州 434023)

0 引 言

Lamb波是最常见的一种平面导波形式。对Lamb波在缺陷板中反射、散射、模式改变等现象的研究,为超声无损检测提供了重要的理论依据。但这些研究多集中于自由薄板的情况,即仅考虑薄板处于真空或空气中且薄板为完全弹性介质,从而不需要考虑能量损失,也就是不需要考虑幅值衰减。目前这种自由薄板中的Lamb波从模型的建立到频散曲线的绘制已有比较成熟的方法[1-4]。

随着工程应用的发展,Lamb波被引入套管井固井水泥胶结质量的评价中[5]。若满足一定条件,Lamb波在圆柱层状套管井中的传播可近似为在层状介质中的传播。Lamb波在上述介质中向前传播时由于能量损失会出现幅值衰减的现象。这种波称为泄漏Lamb波,层状介质中泄漏Lamb波的情况更为复杂。不仅要考虑传播过程中的频散性还要考虑幅值衰减。实践表明,对这种多层介质建模所得到的泄漏Lamb波的模型比自由薄板中的Lamb波模型要复杂得多。若依旧采用自由薄板中Lamb波的数值求解方法将会出现求解困难甚至完全失效的情况。因此,为在固井质量评价中更加有效地应用泄漏Lamb波,本文研究了层状介质中泄漏Lamb波的建模以及频散方程的求解方法,绘制了泄漏Lamb波频散及衰减曲线,以期为泄漏Lamb波在工程中的应用提供一种实用的数值计算方法。

1 层状介质泄漏Lamb波的建模

1950年Thomson[6]首次采用传递矩阵方法对任意层状介质中Lamb波传播进行建模,随后Haskell[7]进一步发展了该方法,并使之在地震学中得到了应用。在此基础上,文献[8-10]给出了针对黏弹性层状介质以及浸液薄板中泄漏Lamb波的研究思路。目前大部分文献对于层状介质中泄漏Lamb波传播的建模仍沿用传递矩阵方法。

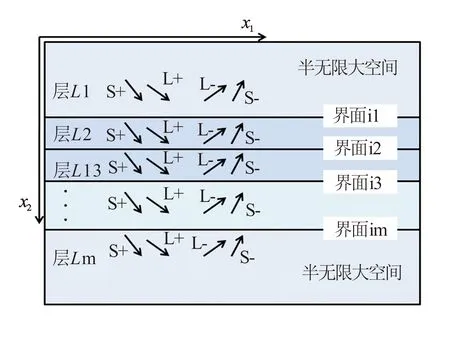
图1 层状介质模型

图1为泄漏Lamb波传播的层状介质模型。可将该模型中的纵波和横波势函数分别设为

(1)

(2)

u(n)=φ(n)+×ψ(n)

(3)

(4)

根据Snell定理以及波数的定义,可将D(n)化简为仅与各层参数及x1方向的波数有关的矩阵。其元素可参考文献[13]。式(4)适用于图1层状介质模型中的所有层以及层内的任意位置。将式(4)分别应用于各层的顶部和底部,并考虑到位移及应力的连续性,可得到关系式

(5)

式中,Lm,top为层m的顶部;[L]L2为各层的传递矩阵[13]。以下将矩阵积[L]L(m-1)…[L]L3·[L]L2记为 [S]。与自由薄板中的Lamb波不同,为了得到泄漏Lamb波的模型,必须考虑图1中模型的上下半空间为非真空的情况。考虑式(4)、式(5)可得到

(6)

(7)

可得

(8)

f(K)=T22·T44-T42·T24=0

(9)

K为前面提到的x1方向的波数。当考虑波在传播过程中能量损失时,常用的处理方法是引入复频率或波数。若引入复波数,则复波数的实部为频率与相速度的比值,虚部对应泄漏Lamb波在x1方向传播时的衰减。求取泄漏Lamb波的频散曲线和衰减曲线即为使频率、相速度和衰减值同时满足式(9),也即求解复频散方程f(K)的0点。

该泄漏Lamb波的频散方程是复超越方程,不存在解析形式的根。必须通过数值方法进行求解,而且该方程的复杂性随着层数的增加而增加。因此,对数值计算方法的效率提出了更高的要求。

2 常用方法及分析

与泄漏Lamb波相关的大部分文献和专著中多采用文献[13]提出的方法求取复频散方程f(K)的0点。其核心步骤:粗略寻根、最优寻根、曲线追踪。①粗略寻根如图2所示,产生如图3所示的频散方程f(K)的幅值变化曲线。当频散方程的幅值处于局部极小值时,将对应一相速度,该相速度和固定频率即构成频散曲线上的一近似点。②最优寻根主要思路是保持某一参量不变而另2项参量以较小步长交替搜索,找到频散方程幅值新的极小点。当极小点处频散方程的幅值与0值的差满足精度要求时,停止搜索,该极小点对应的频率、相速度、衰减值即可作为频散方程的最优根。③曲线追踪时首先需确定2至3个初始最优根,根据这些最优根进行外推以获取新的最优根的预测值,得到预测值后对预测值再进行最优寻根。最终可以得到整个选定模式的频散曲线或衰减曲线。

图2 相速度扫描示意图

图3 频散方程幅值变化曲线示意图

图4 频散方程幅值变化曲线示意图

对上述算法进行验证。在求解自由或浸水钢板Lamb波频散曲线和衰减曲线时可得到满意的结果。当钢板的上下介质声参数为非对称时,模型如表1所示。在粗略寻根后进行最优寻根时,部分极小点对应的频散方程的幅值没有出现趋近于0值的现象,视作无法收敛。为分析原因,固定一个频率进行相速度扫描。得到了如图4的幅值随相速度变化的曲线。显然曲线中的局部极小值点多于图3中的局部极小值点。进一步验证,局部极小值点A、D在最优寻根过程中,频散方程的幅值将逐渐趋近于0,视作可以收敛。局部极小值点B、C进行最优寻根时无法收敛,将导致根的取舍的抉择难度增加,从而增加误判。这种误判是致命的,将直接导致第3步曲线追踪时出现大量错误,以至无法绘制与频散曲线对应的衰减曲线,而且也使得大量时间耗费在无法收敛点的计算上。图5是保留所有误判时a0模式的频散曲线图,其对应参数为表1。可观察到a0模式出现大量间断点,明显不符合模式波的传播规律。表1中将水的横波速度设为较小值(相比纵波速度小2个数量级)。这种处理方式在含流体层的层状介质中较为常见,可避免传播矩阵推导过程中出现矩阵奇异的现象。可以证明,这样做流体层不必特别处理就能得到正确的结果。

表1 层状介质模型参数

图5 保留误判时a0模式频散曲线示意图

3 改进算法及计算结果

由前面的分析,计算泄漏Lamb波频散方程f(K)的0点是获取频散曲线和衰减曲线的关键,其实质是求解复超越方程f(K)的复根。文献[12]中Dayal和Kinral应用二分法和牛顿-弦截法分别求出了频散方程复根的实部和虚部。但在2条频散曲线的交叉点处,求根有可能出现异常[13]。其他方法还有围数积分法、Muller法、Newton-Raphson法等[14]。围数积分法利用了复变函数的广义对数留数定理[15],可以稳定地给出高精度复数根,但由于在解的搜索过程中需要对频散方程进行求导和积分计算,当层数较多时,耗时较长。Muller法也称作抛物线法,同样可求解频散方程的复根,但需要要构造二次插值多项式导致计算略显繁琐。Newton-Raphson法思路简洁适合编程实现且在单根附近具有较高的收敛速度,但对初始近似值的精度要求较高,如果初始近似值的误差较大,则可能给出发散的结果。

综合考虑后的算法在粗略寻根和最优寻根方面做了改进,曲线追踪方法不变。改进后粗略寻根的目的是尽可能以较小的误差得到到频散方程0点的初始近似值,然后在最优寻根中利用初始近似值和Newton-Raphson方法进行迭代计算得到0点的最优值。搜索初始0点近似值时,首先仍然是采用前面提到的文献[13]的方法,得到如图4所示的曲线。然后在图4中的局部极小值点及其附近进行局部峰的搜索,最后判断局部峰内是否确定存在0点。若存在0点,则局部峰所处位置即为所求0点的近似值。

图6为某一固定频率点形成的局部峰形状示意图。图6中水平轴分别对应离散化了的相速度和衰减。离散间距需足够小,以使得局部峰凸显出来,垂直轴对应H(K)的幅值。在固定频率处相速度和衰减同时参与了扫描,形成了有关H(K)幅值的三维图,避免了图4中粗略寻根时对Lamb波衰减预估中的人为因素。

图6 频散方程在某固定频率点处的局部峰形状图

得到H(K)的幅值,通过直接搜索的方法确定局部峰值点。图7对应的是某一固定频率处离散的相速度—衰减平面示意图。图7中矩形所选区域对应的H(K)已离散化,离散化值为H(m,n),m,n=1,2,3,…。若H(m,n)为该区域的最大值,则H(m,n)即为所求局部峰。相应的频散方程f(K)在该处就可能存在0点。

为进一步降低误判率,可引入函数

(10)

该函数用来量化离开局部峰顶点时H(m,n)的下降速度。下降速度越快,局部峰处存在0点的可能性越大。因此可将Γ>ε作为判断标准,ε为小于1的正数需根据经验和实际情况选取。当计算得到的Γ满足Γ>ε判定为局部峰,即可能存在0点的区域,可用于下一步继续分析,否则认为是无0点存在的普通小突起。

利用上述方法获取局部峰,即得到了频散方程f(K)存在0点的可能区间。再判断在已求得的可能区间是否确定存在0点。由复变函数理论可知,如果f(K)在简单闭曲线C上与C内解析,且在C上不等于0,那么f(K)在C内0点的个数等于1/2π乘以当K沿C的正向(逆时针)绕行一周f(K)的辐角的改变量。可表示为

(11)

式中,N表示0点个数;ΔC+Argf(K)表示K沿C正向绕行1周时f(K)辐角的改变量。在图7中如果H(m,n)已确认为局部峰,则利用辐角原理判断0点个数时绕行路径C即指H(m,n)处的虚线方框。如图7中箭头所示,显然它是简单闭曲线。由频散方程f(K)知道,在路径C内无极点存在,且对于实际的物理系统总认为是连续的可导的。因此,只考虑f(K)在C内与C上是解析的且在C上不为0(C上为0则该点即为所求0点)的情况。

图7 相速度—衰减平面示意图

计算机在计算辐角改变量之前需要先对路径离散化,离散化后相邻2点辐角的改变量表示为

Δi=Δ[Ki,Ki+1]Argf(K)i=1,2,3,…M

(12)

式中,M为路径C上总的离散点数,且Km+1与K1点重合。那么由绕行路径C计算得到的0点个数为

(13)

同样,由复变函数理论知道,若路径C在离散化过程中满足|Δi|≤π,i=1,2,3,…M,则

Δi=Arg [f(Ki+1)/f(Ki)]i=1,2,3,…M

(14)

文献[16]中给出了详细的针对绕行路径C的离散化方法,应用该方法可以使离散化的Δi满足|Δi|≤π。文献[16]还给出了完整的基于FORTRAN的源代码。

将式(14)带入式(13)后可得

(15)

式(15)用于判断局部峰内是否确定存在0点。如果存在多个0点,可以将图7中离散点的间距进一步减小,总可以得到只包含1个0点的局部峰。

当确定局部峰内包含0点,可以采用文献[13]的最优寻根方法计算最优根。但这种交替式的搜索方式收敛速度较慢。考虑到此时可以取离局部峰最近的离散点作为0点的近似值,Newton-Raphson方法可以利用该近似值作为初始近似值进行迭代计算。此时,迭代公式为

(16)

式中,x0、y0、x1、y1为实数;K0、K1为不相等的初值,均选自局部峰附近的离散点,且满足|f(K1)|<|f(K0)|。具体计算步骤

(1) 局部峰附近选定2个初始值K0、K1,计算相应的函数值f(K0)、f(K1);

(2) 代入式(12)的迭代公式计算Ki+1的值;

(3) 如果出现|Ki+1-Ki|<ξ的情况,则终止迭代计算,Ki+1即为所求,否则转(4),ξ为给定精度值;

(4) 如果迭代计算超过最大指定次数N,则认为迭代过程不收敛,计算失败,否则转(2)继续进行迭代计算。

通过以上步骤可以顺利得到频散方程f(K)0点的最优根,为曲线追踪提供有力保障。多次计算后发现,在求取局部峰的过程中,当ε选择合适时,局部峰内无0点存在的几率很小。所以,对于局部峰内是否存在0点的判断只在频散曲线出现异常时引入。例如曲线追踪过程中在预测值附近并未搜索到局部峰的存在,原因可能是ε设置得过大或是频散曲线波动过大。此时可适当调低ε设置值并扩大搜索局部峰的范围。这种情况可能导致多个局部峰的出现,此时可引入0点判断的算法,排除无0点存在的普通小突起的干扰。采用这种可剥离式的算法可大大提高计算速度。

图8 钢板位于慢水泥与水之间时的a0模式频散曲线图

图9 钢板位于慢水泥与水之间时的a0模式衰减曲线图

图10 钢板位于快水泥与水之间时的a0模式频散曲线图

图11 钢板位于快水泥与水之间时的a0模式衰减曲线图

图8、图9采用改进的算法分别得到了钢板位于慢水泥与水之间时a0模式的频散曲线和衰减曲线。参数见表1。由曲线可知相速度被慢水泥的纵波速度截为2支,即图8中在200 kHz附近出现了2个模式波。图10、图11中钢板位于快水泥与水之间,此时快水泥的纵波速度大于a0模式的最大相速度,横波速度仍然将衰减曲线截为2支,但相速度所受影响并不明显。图8至图10与文献[17]中利用商业软件DISPERSE所计算曲线完全一致。

4 结 论

(1) 泄漏Lamb波频散和衰减曲线的绘制在工程应用中具有重要意义。已有文献的相关算法多适用于自由或浸水的层状介质。当层状介质上下半无限介质的声学参数为非对称时,在寻找最优根的过程中,出现误判的几率增大。

(2) 对层状介质中泄漏Lamb波进行建模并对相应的频散方程进行分析,设计了一种针对该频散方程的数值计算方法。该方法在局部峰附近利用复变函数理论,对根的存在性予以明确的判断,从而极大地降低了最优根的误判率。

(3) 利用该方法可准确计算并绘制层状介质中泄漏Lamb波频散和衰减曲线,具备一定的通用性。

参考文献:

[1] 曹正敏, 林莉, 李喜孟. 兰姆波频散曲线的绘制与试验验证 [J]. 理化检验: 物理分册, 2008, 44(9): 193-199.

[2] 艾春安, 李剑. 兰姆波频率方程的数值解法 [J]. 无损检测, 2005, 27(6): 294-296.

[3] 艾春安, 吴安法. 兰姆波频散方程的分析及数值迭代算法 [J]. 上海航天, 2008, 28(5): 42-44.

[4] 阎石, 张海凤, 蒙彦宇. Lamb波频散曲线的数值计算及试验验证 [J]. 华中科技大学学报: 城市科学版, 2010, 27(1): 1-4.

[5] 王华, 陶果, 尚学峰, 等. 轻质水泥固井质量声波测井评述与方法研究 [J]. 测井技术, 2014, 38(2): 165-173.

[6] Thomson W T. Transmission of Elastic Waves Through a Strified Solid [J]. J Appl Phys, 1950, 21: 89-93.

[7] Haskell N A. Dispersion of Surface Waves in Multilayered Media [J]. Bull Seim Soc Am, 1953, 43: 17-34.

[8] Nayfeh A H, Chimenti D E. Elastic Wave Propagation Influidloaded Multiaxial Anisotropic Media [J]. Acoust Soc Am, 1991, 89: 542-549.

[9] Cervenka P, Challande P. A New Efficient Algorithm to Compute the Exact Reflection and Transmission Factors for Plane Waves in Layered Absorbing Media (Liquids and Solids) [J]. Acoust Soc Am, 1991, 89: 1579-1589.

[10] Hosten B. Bulk Heterogeneous Plane Waves Propagation Through Viscoelastic Plates and Stratified Media with Large Values of Frequency Domain [J]. Ultrason., 1991, 29: 445-450.

[11] Chimenti D E, Nayfeh A H, Butler D L. Leaky Rayleigh Waves on a Layered Halfspace [J]. J Appl Phys, 1982, 53: 170-176.

[12] Dayal V, Kinra V K. Leaky Lamb Waves in an Anisotropic Plate I: An Exact Solution and Experiments [J]. J Acoust Soc Am, 1989, 85: 2268-2276.

[13] Lowe M J S. Plate Waves for the NDT of Diffusion Bonded Titanium [D]. London: University of London, 1993.

[14] 易大义, 沈云宝, 李有法. 计算方法 [M]. 2版. 杭州: 浙江大学出版社, 2003: 150-154.

[15] 张忠诚, 王成. 对数留数定理的推广及应用 [J]. 洛阳大学学报, 2006, 21(2): 20-22.

[16] Xingren Ying, Katz I N. A Reliable Argument Principle Algorithm to Find the Number of Zeros of an Analytic Function in a Bounded Domain [J]. Numer Math, 1988, 53: 143-163.

[17] Froelich B. Multimode Evaluation of Cement Behind Steel Pipe [J]. J Acoust Soc Am, 2008, 123: 3648.