低渗透率储层流度计算改进方法探讨

张国栋, 陈忠云, 张志强

(1.中海石油(中国)有限公司上海分公司, 上海 200030; 2.中海油田服务股份有限公司, 河北 三河 065201)

0 引 言

流度值是表征储层渗透性大小和进行产能预测的关键参数,通过测压获得的流度信息能够真实反映井眼环境下储层的渗透能力,以此开展储层产能评价等工作[1-5]。近年来,针对低渗透率储层,在西湖凹陷进行了大量的测压作业,目的是通过流度值进行储层物性评价和天然气产能预测[6],以及指导测试工艺优化,因此流度数值的准确性至关重要。低渗透率储层流度计算存在两大难点,一是储层渗流能力差,压力恢复难以出现稳态流;二是受超压影响,压力值难以恢复稳定,致使计算得到的流度值往往偏大。本文深入剖析了低渗透率储层难以出现稳态流的原因,提出了具体改进措施,取得了良好应用效果,使低渗透率储层测压获得的流度值更加精确。

1 低渗透率储层压降流度偏大原因分析

1.1 流度定义与计算

流度为渗透率除以黏度,mD/cP*非法定计量单位,1 mD=0.987×10-3 μm2;1 cP=1 mPa·s,下同,它是基于达西定律推导出来的,数学推导公式为

达西公式

(1)

流度计算公式[7]

(2)

式中,K为渗透率;μ为黏度;Q为流速;L为长度;S为面积;Δp为压差;Cpf为仪器形状系数,使用不同的探针有不同的数值;V为抽吸体积;t为流动时间。

流度是基于达西定律的物理参数,在测压时必须满足2个基本条件:①要出现稳态流;②有稳定的压力差,即压力恢复要稳定。图1是标准的压力时间恢复曲线示意图。一次完整的测压作业可分为5个阶段,即坐封、泵抽、流体流入管线、压力恢复和解封。测压时,如果可以出现图1所示的稳态流段,则可以通过压降流度公式得到准确的流度值。然而,在实际测压过程中,低渗透率储层基本无法出现稳态流阶段。

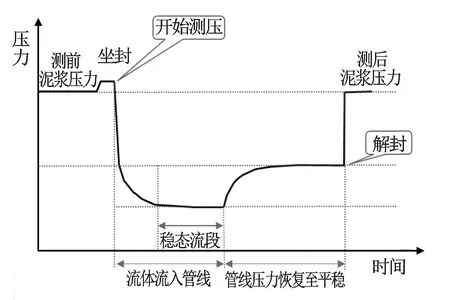
图1 单点测压压力时间曲线

1.2 低孔隙度渗透率储层测压流型分析

相比于中、高孔隙度渗透率的储层,低渗透率储层的特点是单位面积下的供液能力小,在探针抽吸速度一定,或者抽吸时间有限的情况下,难以使地层供液速率达到抽吸速率,也就无法出现稳态流。一般情况下,低渗透率储层测压时会有a、b这2种压力时间恢复曲线流型(见图2)。a流型为当抽吸速率小于地层最大流速,但是抽吸时间不够长,压力下降幅度还没有达到出现稳态流时,便停止抽吸;b流型为当抽吸速率大于地层在最大压差下的流速,即地层在最大压差下也难使其供液速率达到抽吸速率。例如,测压时用的最小抽吸速率是30 cm3/min,抽吸体积是5～10 cm3,如果在一定的抽提时间和压差下,地层的供液能力达不到30 cm3/min,此时无法出现稳态流。

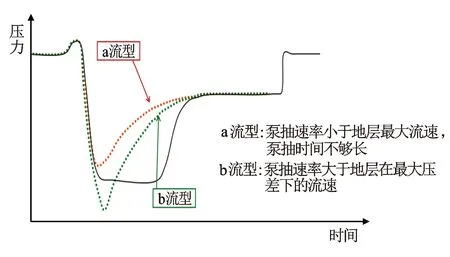
图2 低渗透率储层测压压力时间曲线流型示意图

1.3 非稳态流下的压降流度值

非稳态流情况下不能使用达西定律计算流度,由于在测压时无法测量地层真正的地层流动速率Qf,使用的是抽吸速率Qdd,对于低渗透率储层Qf值远小于Qdd值,如果将Qdd带入式(3)计算,那么得到的流度就会偏大。因为只有出现稳态流时Qf=Qdd。

(3)

DX27-5井是西湖凹陷1口深层探井,其主要目的层在4 300 m以下,基本为低渗透率储层。该井在4 336 m和4 341 m进行了电缆测压,2个点的物性大小基本相当,其中子—密度孔隙度在11%左右。测压时,分别选用了不同的测压参数,4 336 m处抽吸体积为5 cm3,抽速约为1.8 cm3/s,测压过程没有出现稳态流,计算得到的流度为10.1 mD/cP;4 341 m处抽吸体积为10 cm3,抽速约为0.8 cm3/s,该点出现了标准的稳态流曲线,其计算得到的流度为5.6 mD/cP,具体压力恢复曲线如图3所示。

从上述2点的应用实例可以看出,当测压无法得到稳态流时,计算得到的流度值会明显偏大,这样就会高估储层物性,误导后续测试决策。

图3 DX27-5井4 336 m和4 341 m处压力恢复曲线图

2 低渗透率储层流度计算改进方法

2.1 面积积分法

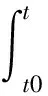
(4)

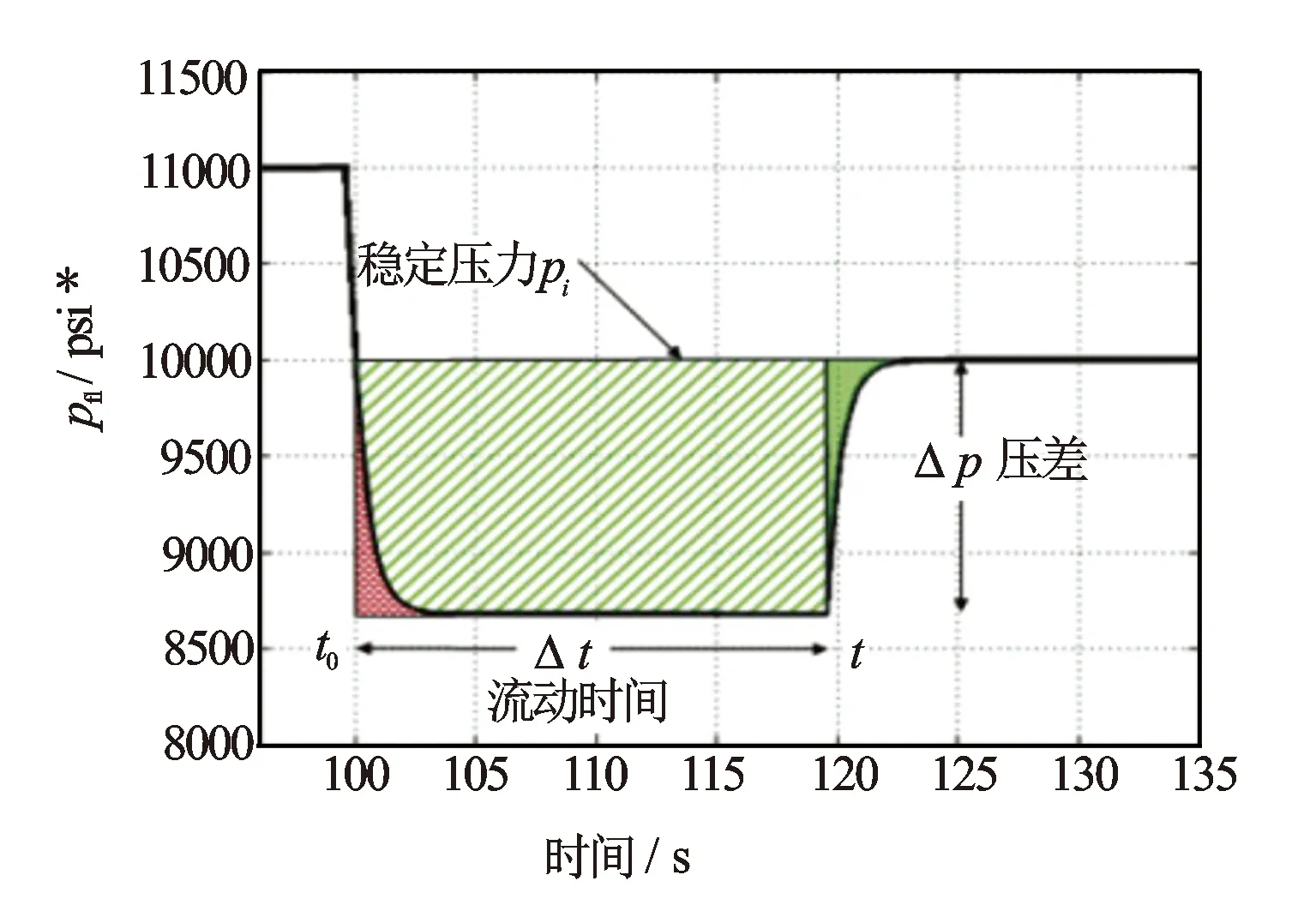
图4 理想稳态流压力时间曲线*非法定计量单位,1 psi=6.89×103 Pa,下同

公式改进后,既能反映压力降落过程的压力变化情况,也可反映压力恢复过程的压力变化情况。但是该公式仍然是基于稳态流计算理论,它只是通过数学的方法对未出现稳态流的压力响应情况做了数学校正,计算得到流度值相对准确,结果仍会偏大。图5是2种流度计算方法效果对比,对于低渗透储层同一测压点,面积法计算得到的流度为0.59 mD/cP,常规计算方法得到的流度为0.94 mD/cP,两者数值相差18%。

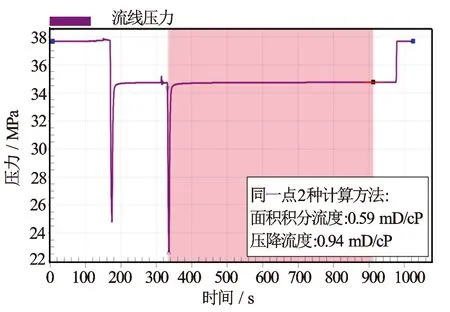
图5 非稳态流情况下2种流度计算方法效果对比

2.2 流速校正法

Qac=Qf-Qdd

(5)

(6)

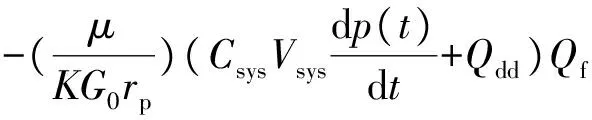
(7)

式中,Qac为管线中的流速;Qf为地层的流速;Qdd为泵抽的流速;Ct为压缩系数;p*为地层压力;p(t)为测量的压力;K/μ为地层流度;G0为几何因子;rp为探针半径。

通过式(5)、式(6)求得Qf值,根据式(7)绘制压力和地层流速中的直线关系图(见图6),从图6中能够得到斜率和截距p*(地层压力),根据回归得到斜率值,可以计算地层的流度值以及回归的地层压力。

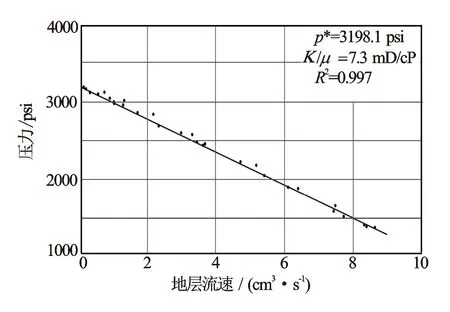
图6 FRA算法测试压力与地层流量关系图

实际作业过程中,低渗透率储层测压点难以回归出相关度高的公式(见图7),数据点呈波浪状分布,数据点相关度非常低。分析认为是由于储层渗透率非均质性很强,随着抽吸的进行,球形流波及到的不同深度地层的渗透率有所变化,从而造成了数据点不稳定,地层流速与时间散点图能比较直观地体现(见图8)。如果不能回归出相关度较高的关系式,利用RFA算法计算储层流度值也不准确,为此提出了校正方法。以DX27-5-1井4 341.01 m处测压数据为例说明校正方法和过程。

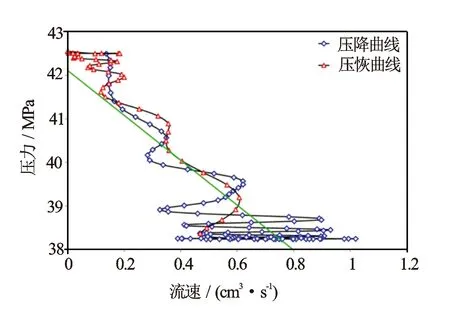
图7 DX27-5井4 336 m处压力与地层流速关系图

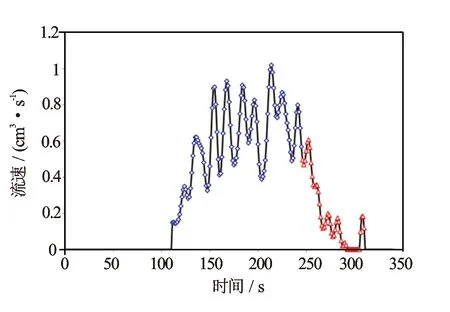
图8 DX27-5井4 336 m处时间与地层流速关系图

(1) 首先将流速时间曲线进行面积补偿平滑,得到平滑后回归的曲线公式(见图9)。

图9 流速—时间曲线数据回归

(2) 根据平滑后回归公式,将各个点的流量进行重新计算。

(3) 将重新计算的流量和压力数值进行回归,可以得到相对更加准确的回归曲线(见图10)。

图10 压力—流速曲线数据回归

表1是DX27-5-1井测压点校正前后流速和流度的对比,校正前12个测压点的平均流度是4.1 mD/cP,校正后平均流度为2.3 mD/cP。可见,如果不进行非稳态流度校正,将会明显高估储层的渗透能力。

FRA算法在求取地层流速时是基于达西定律的,但实际测压时,坐封后管线中的压力和地层压力存在一定的压力差,这个和达西的实验存在一定的区别,所以第1次抽吸时Qac=Qf-Qdd并不是一个完全相等的公式,当井筒压力与地层压力基本相当或者略高于地层压力时,使用FRA才比较准确,所以使用第2次抽吸的数据进行流度计算才更加准确。另外对于一些非均质性很强的特低渗透率气层,随着抽吸的进行,球形流波及到的不同深度地层的渗透率有所变化,也能造成流速的不稳定(见图8)。

2.3 测压参数统一法

不管是面积法和FRA计算方法都存在一定的缺陷。在实际测压作业中,不同公司、不同工程师,在遇到低渗透率储层时,采用的测压参数不尽相同,抽速不同、体积不同、等待时间不同,最后得到的流度值大小无法进行对比,特别是一些较致密的点,压力恢复难以稳定,问题就更加突出,大大降低了测压的价值。据此,提出了统一测压测量参数方法。例如,在DX27-5井测压前,根据电阻率和三孔隙度数据,以及区域资料,对测压点的储层物性做一个预判,若属于低渗透率储层,则采取如下参数。

表1 DX27-5井测压点校正前后流速与流度对比表

图11 统一测量参数不同低渗透率点流度值对比

(1) 抽吸速度尽可能小,0.5 cm3/s,如果仪器允许,抽吸速率还可以更低。

(2) 抽吸次数3次,抽吸次数越多,超压现象越轻,压力值越稳定。

(3) 第1次抽吸量5 cm3,抽速为1 cm3/s,恢复5～7 min;第2次抽吸10 cm3,抽速为0.5 cm3/s,恢复8～10 min或稳定,第3次抽吸5 cm3,抽速为0.5 cm3/s,恢复5～7 min或稳定。

当所有点的测压参数统一后,可以确保在无法获得绝对流度值的情况下得到不同测压点之间较为准确的数值(见图11)。统一测量参数后,每个点绝对流度值可能是不准确的,但是可以保证不同点间的相对大小准确;从而能够利用流度值在1口井或不同井间进行物性对比,能更大限度地发挥测压的作用。

3 结论与认识

(1) 低渗透率储层无法出现稳态流原因在于单位面积供液速率达不到抽吸速率,致使压降法得到的流度值偏大。在低渗透率储层测压时,抽吸速率要尽可能低,抽吸时间要更长,才有可能在低渗透率点测压时获得稳态流压力恢复曲线,目前斯伦贝谢MDT仪器和贝克休斯RCI仪器其最小抽吸速率为0.25～0.5 cm3/s,测压精度偏低,很难适用于1 mD/cP流度以下储层测压。

(2) XPT是斯伦贝谢新一代测压仪器,特点是管储效应更小,只有30 cm3,压力计精度更高,最小抽吸速率可以达到0.02 cm3/s,该仪器技术指标参数能够满足低渗透率储层测压时低管储效应、低轴速要求,建议今后针对低渗透率储储层采用XPT仪器。

(3) 面积积分法和FRA算法都能在一定程度上使流度值更加精确,但还存在一定的局限性。面积法只是数学修正,没有实际物理意义;FRA算法实际应用时,需对流速进行人为校正。

(4) 低渗透率储层测压时,采用参数统一法更具有实际意义,只有在流度值相对大小确定后才能开展不同深度段、不同井之间的物性对比,为测试选层,产能预测提供更加准确的参考依据。

参考文献:

[1] Lee J, Michaels J, Atlas B. Enhanced Wireline Formation Tests in Low-permeability Formations: Quality Control Through Formation Rate Analysis [C]∥SPE 60293 prepared for presentation at the 2000 SPE Rocky Mountain Regional/Low Permeability Reservoir Symposium and Exhibition, Denver, Colorado, 2000.

[2] 孙建孟, 任怀建, 赵文杰, 等. 应用节点分析法进行油气井产能预测研究 [J]. 测井技术, 2006, 30(4): 350-353.

[3] 孙建孟, 运华云, 冯春珍. 测井产能预测方法与实例 [J]. 测井技术, 2012, 36(6): 628-634.

[4] 林伟川, 冯春珍, 赵慧, 等. 低孔隙度低渗透率储层孔隙压力流体评价方法 [J]. 测井技术, 2006, 30(4): 334-337.

[5] 张聪慧, 刘树巩, 李义, 等. 利用电缆地层测试资料进行低渗储层流度计算和产能预测 [J]. 中国海上油气, 2013, 23(1): 43-45.

[6] 张国栋, 施荣富, 王聃, 等. 东海西湖凹陷低孔渗储层电缆取样方法创新和应用 [J]. 中国海上油气, 2015, 27(2): 39-43.

[7] George Stewart, Manfred Wittmann. Interpretation of the Pressure Response of the Repeat Formation Tester [C]∥SPE8362 the 54th Annual Fall Technical Conference and Exhibition of the Society of Petroleum Engineers of AIME, in Las Vegas, Nevada, September 23-26, 1979.

[8] Dussan V E B. A Robust Method for Calculating Formation Mobility with a Formation Tester [C]∥SPE13302, SPE Reservoir Evaluation & Engineering April 2011.

[9] Kasap E, Huang K, Shwe T. Robust and Simple Graphical Solution for Wireline Formation Tests: Combined Drawdown and Buildup Analyses [C]∥SPE36525, Prepared for Presentation at the 1996 SPE Annual Technical Conference and Exhibition. Denver, Colorado, 1996.

[10] Kasap E, Huang K, Shwe T, et al. Formation-rate-analysis Technique: Combined Drawdown and Buildup Analysis for Wireline Formation Test Data [J]. SPE Reservior Eval & Eng, 1999, 2(3): 271-280.