Hoek-Brown准则在致密砂岩抗剪强度参数测井解释中的应用

尹帅, 丁文龙, 张宁洁, 谢非, 焦乃林

(中国地质大学能源学院,海相储层演化与油气富集机理教育部重点实验室,页岩气资源战略评价国土资源部重点实验室, 北京 100083)

0 引 言

致密砂岩储层是目前油气勘探、开发最为现实的领域,岩石含有多种矿物组分且往往经历了强压实及复杂成岩演化等致密化进程,岩石内部具有较强的非均质性及各向异性[1]。在复杂地质因素综合作用影响下,致密砂岩强度属性特征在纵横向上发生了较大程度转变[2-5],其中内聚力(C)和内摩擦角(φ)是衡量岩石抗剪能力的2个重要力学参数[1],了解这2个参数的变化可以为工程施工、沉积及成岩演化、应力场模拟及裂缝预测等方面提供重要参考。这2个参数一般需通过直剪测试或三轴抗压测试获得[6],对于深部致密砂岩储层,地层处于较高的应力环境中,利用三轴抗压测试获取岩石抗剪强度参数的方法可行,本文即采用该方法获得岩石内聚力及内摩擦角。

随着超声波技术[7-8]的发展,可以利用声波测井资料对地层岩石各力学参数进行计算,通过校正获得相应抗剪参数的静态结果。对于致密砂岩储层,受矿物组分、构造应力、地层压力及微裂缝等方面因素的影响,地层岩石内聚力和内摩擦角纵向离散度较大,给测井解释带来了新的挑战。研究表明,Hoek-Brown准则所定义的部分参数可以与声学测试结果建立较好的定量关系[3,6,9]。同时,Hoek-Brown准则由于考虑了岩石三轴测试中剪切破裂曲线的非线性变化,往往认为所定义参数能代表岩石真实力学属性及变形、破坏机制[9]。由于前人未将该准则应用于岩石抗剪强度参数的测井解释中,本文提出基于Hoek-Brown准则的致密砂岩储层抗剪强度参数测井评价方法,扩展了岩石抗剪强度参数的测井评价途径,可以为地层岩石抗剪性能综合评价提供参考。

1 样品、测试流程及抗剪强度参数取值

1.1 样品及测试流程

样品取自塔中地区志留系海相致密砂岩地层,埋深大于5 000 m,地层有油气显示。样品加工后尺寸为25 mm×50 mm,共分4组,编号为1～4,每组4个,共16个。镜下显微组分鉴定结果表明其成分主要包含石英,平均含量61.5%;长石,平均含量9.4%;沉积岩岩屑,平均含量20%;泥质填隙物,平均含量4.13%。常规物性测试结果表明,致密砂岩样品体积密度为2.26～2.49 g/cm3,孔隙率为4.48%～12.7%。采用MTS岩石物理测试系统进行三轴力学与声学同步测试实验,轴压最高伺服1 000 kN,压力传感器误差低于1%,位移分辨率为0.000 1 mm。

实验方案:首先将加工好的致密砂岩样品饱水,在真空罐中饱和3 d。然后进行三轴测试,测试温度为25 ℃。4组样品中每组4个分别设定围压值(σ3)为0、22、44 MPa和65 MPa。对于单轴测试,轴向以大约3.5×10-3s-1应变率加载直至试样破坏,记录整个过程轴向应力σ1及应变变化。三轴测试加载路径及加载方式:首先保持轴向3 kN左右载荷不变,以0.05 MPa/s加载围压,待围压加至设计值(22、44 MPa和65 MPa)后保持围压不变,轴向以大约3.5×10-3s-1应变率施加载荷,直至岩样发生破坏,应力出现急剧跌落,实验结束,应力、应变数据通过计算机自动读取。

1.2 抗剪强度参数取值结果

根据线性Mohr-Coulomb准则[10]求取致密砂岩岩样抗剪强度参数。依据该准则,岩石内聚力和内摩擦角可以根据岩样破坏时轴向应力σ1和有效围压σ3之间的关系由式(1)确定。

(1)

利用式(1)对4组样品的σ1和σ3值分别进行线性回归,根据拟合线的斜率可求得φ值,进而根据截距可求得C值。各组样品拟合曲线见图1,拟合效果参数(R和F)及计算结果见表1。回归中,置信度默认为95%,R为相关系数,F为显著性统计量,从拟合效果来看(见表1),R值接近1,表明拟合效果非常好;F值均大于0.05,表明各组样品测试的σ1和σ3值之间均非常显著,最终根据式(1)计算各组样品相应C、φ值(见表1)。

表1 拟合参数及计算结果

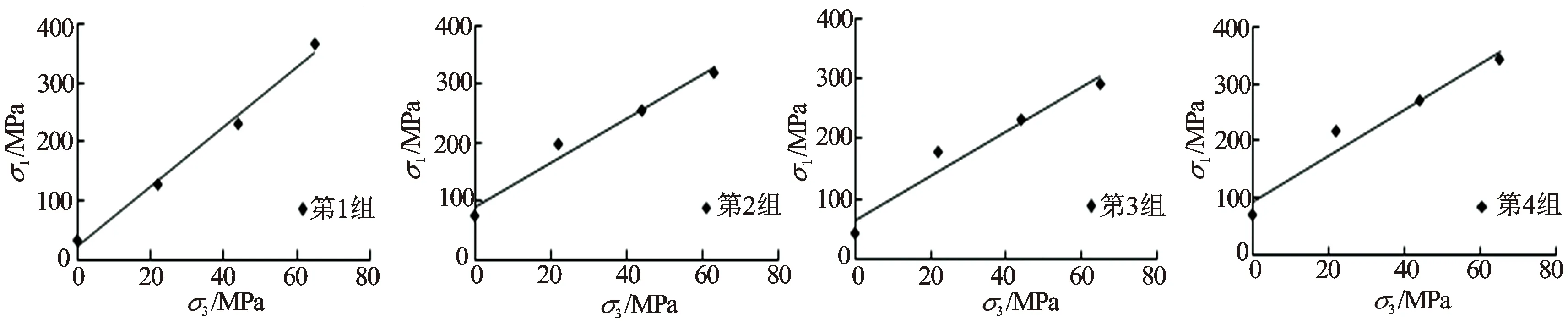
图1 致密砂岩三轴强度拟合曲线

2 Hoek-Brown准则参数取值

Hoek-Brown准则是Hoek原为定义岩石破裂应力和正常应力之间的关系而发展起来的强度预测理论[9],经过不断完善后于1995年被修改为一般通式[11]。表达式为

(2)

式中,mb、s和a分别为该准则中的定义参数,无量纲。mb可以调节摩尔包络线的倾斜程度,取值大代表硬度大的岩体,反之代表硬度小的岩体。s取值范围为0～1,当取1时代表岩体完整无裂缝或节理等构造,当取0时代表岩体严重破碎。a主要用来调节包络线的曲率,取值范围在0～1。mb、s和a的表达式分别为

(3)

(4)

(5)

式中,D代表原位岩体受干扰程度,未受干扰取0,严重受干扰取1。由于所取岩心均为完整样,本文主要对未受干扰条件下岩样进行评价,所以取D=0。

对于4组致密砂岩岩样,文献[3]基于反算法已经给出了具体H-B参数取值结果。具体方法:对于各组完整致密砂岩样品,首先假设各组样品的GSI值均为100[12],由式(5)可知对应a=0.5;对单组样品的4组σ1、σ3分别代入式(2)进行非线性最小二乘法拟合,从而求得4组样品的mb值(分别为24.36、6.15、7.96、7.89);s值取平均值约为0.75,这可能与样品中存在微裂缝有关。对式(2)进行变形,用s和D表示GSI。

GSI=lns(9-3D)+100

(6)

根据s和D值变化范围及(6)式可知各组样品GSI主要分布在89.2～98.3[3],根据式(4)可知mb与GSI存在指数关系。在指定范围下用式(7)求取各组致密砂岩样品mi平均值,然后可根据式(8)表示各组岩样GSI值[3]。

(7)

(8)

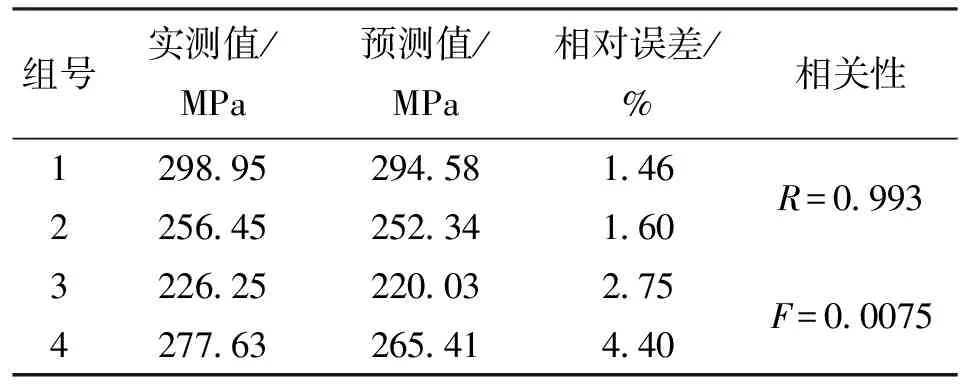
表2 三轴测试拟合结果对比

根据式(8)即可求得1～4组致密砂岩样品的GSI值,按顺序分别为100、70.79、78.01、77.77。对于该计算方法的预测效果,可以通过将基于该方法的岩样三轴抗压强度拟合值与实测值对比进行判定(见表2)。各组致密砂岩岩样三轴抗压强度预测值与实测值间极为相符,表明所计算的各H-B参数可靠。

3 基于H-B准则岩石抗剪强度参数解释方法

多种利用H-B准则预测岩石抗剪强度参数的方法经概括归纳具有较高预测精度的方法主要包括以下3种。

方法1:通过定义单轴参数对岩石C、φ进行估值的方法(简称单轴参数法)。

该方法通过定义σcm(单轴抗压强度)和σtm(单轴抗拉强度)对岩石的C、φ进行估值。对式(2)进行变形,当σ3=0时,σcm可表示为式(9);当σ1=0时,σtm可表示为式(10)。此时岩石C、φ值可以分别通过式(11)和式(12)求取[4-5]。

(9)

(10)

(11)

(12)

方法2:通过定义有效正应力和剪应力参数对岩石C、φ进行估值的方法(简称有效应力法)。

(13)

(14)

(15)

(16)

图2 内聚力及内摩擦角估值结果对比图

方法3:基于狭义H-B准则修正方法的岩石C、φ估值方法(简称狭义H-B修正方法)。

该方法又叫等效抗剪参数方法,建立在大量单、三轴试验及统计分析基础上,由Hoek等提出[9-10]。通过定义一系列中间参数,最终通过式(17)和式(19)分别求得岩石φ及C值。

(17)

H=6amb(s+mbσ3n)a-1

(18)

(19)

(20)

4 测井解释结果对比

利用上述3种基于H-B准则的方法对4组致密砂岩岩样C、φ值进行估算,结果见图2。对于C值,3种方法预测结果相比实测值偏低;对于φ值,除了方法3外,另外2种方法的预测结果相比实测值偏高。虽然利用3种方法直接计算出的各组致密砂岩样品C、φ值效果不佳,但图2中,4组样品C、φ值变化趋势基本一致。可以对上述3种方法C、φ值计算结果分别进行校正,校正公式为

方法1:Ca=1.572Cb+2.187

(21)

方法2:Ca=2.957Cb+4.158

(22)

方法3:Ca=1.376Cb-1.823

(23)

方法1:φa=0.345φb+18.66

(24)

方法2:φa=0.419φb+7.59

(25)

方法3:φa=-0.081φb+40.12

(26)

式中,Ca为修正后C值,MPa;Cb为修正前C值,MPa;φa为修正后φ值,(°);φb为修正前φ值,(°)。

利用上述校正公式分别对4组样品C、φ值预测结果进行修正,修正后的3种方法预测结果见表3。修正后C、φ预测效果相比图2结果而言具有显著提高。对于平均相对误差,修正后方法1的C约为19.44%,φ约为2%;方法2的C约为19.12%,φ约为2.16%;方法3的C约为26.24%,φ约为5.95%。C值相对较高的相对误差主要是由于第1组样品所造成的,因为该组样品C实测值只有5.15 MPa,基数小,造成相对误差偏高。4组样品的φ值预测结果平均相对误差均不大,表明预测效果非常好。平均绝对误差,方法1的C约为2.29 MPa,φ约为0.72°;方法2的C约为2.35 MPa,φ约为0.78°;方法3的C约为3.12 MPa,φ约为2.28°。平均绝对误差整体预测结果,预测效果较好,表明本文基于H-B准则预测致密砂岩抗剪强度参数的方法可行。

由于方法1和方法2的预测效果略好于方法3,方法1的预测效果最好,本文优选方法1对单井目的层致密砂岩井段C、φ值进行测井解释(见图3)。

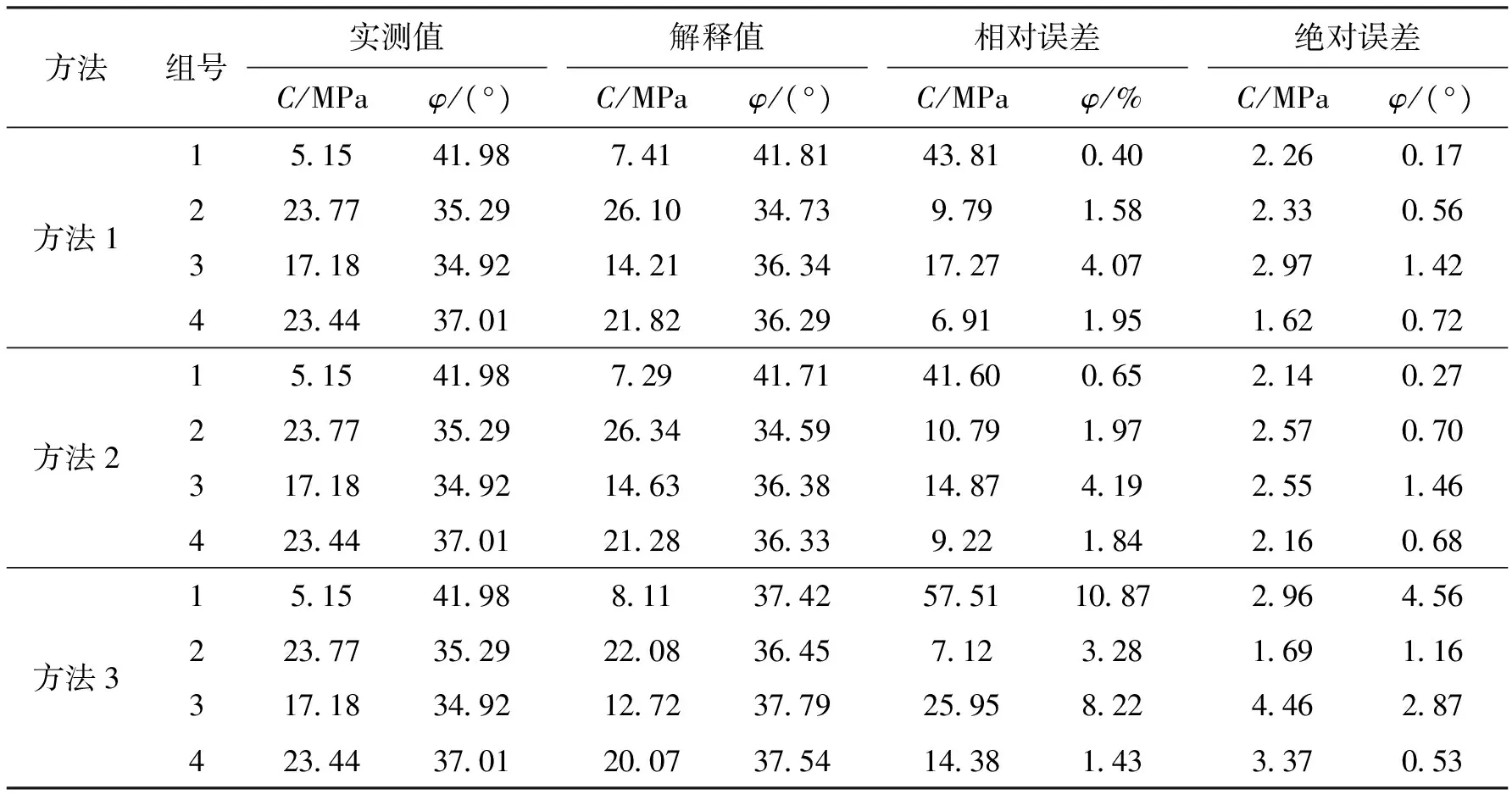
表3 基于H-B准则的岩石C、φ值预测结果(修正后)

图3 单井目的层岩石抗剪强度参数测井解释成果图*非法定计量单位,1 ft=12 in=0.304 8 m,下同

从测井解释结果来看,修正后的地层岩石C值略大于修正前,而修正后的φ值略小于修正前,与前述实验及计算结果一致。对于该井段上部致密砂岩地层井段,泥质含量(Vsh)相对较低,对应地层岩石C值相对较高,而φ值相对较低;对于下部高泥质含量井段,如5 510～5 550 m地层,对应岩石C值相对较低,而φ值相对较高。测井解释结果与地层实际情况具有较好的一致性。

为了进一步说明该研究方法的有效性,对修正前后的目的层C、φ值测井解释结果分别作频数分布图,分别见图4及图5。图4中,修正前后地层岩石C值均呈近似正态分布[13]的特征,修正前C值主要分布在3～16 MPa,修正后C值主要分布在10～26 MPa。由前述实验测试结果可知,所测试致密砂岩C值分布在5～24 MPa,4组致密砂岩样品中有3组(占75%)的C值均大于17 MPa,与修正后的C值预测结果较为一致(见图4)。表明本文所提出的C值修正公式可靠,测井解释结果合理。

对于φ值测井解释结果,从图5可以看出,修正前后地层岩石φ值频数分布特征较为一致,修正前φ值主要分布在7°～67°,离散度较大;修正后φ值主要分布在22°～43°,离散度相对较小。由前述实验测试结果可知,所测试致密砂岩φ值分布在34°～42°,虽然图5所示修正前后地层岩石φ值频数分布图中均涵盖该φ值变化范围。但从一些文献中可以查出,致密砂岩强度高,内部结构特征复杂,内摩擦角变化幅度较大,φ值变化范围一般在25°～50°,因此图5修正前的φ值解释结果明显与实际不符,修正后的结果更符合实际。也表明所提出的φ值修正公式可靠,测井解释结果合理。

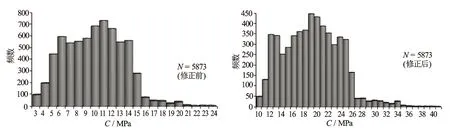
图4 修正前后基于H-B方法岩样内聚力测井解释结果频数分布图

图5 修正前后基于H-B方法内摩擦角测井解释结果频数分布图

5 讨论及结论

影响室内三轴测试确定的致密砂岩C和φ的因素有很多,例如温度、饱水率、饱水时间[14]、矿物及泥质等组分含量[15]、有无夹层、夹层界面粗糙度、起伏差[16-17]、加载条件等[18-19]。对于不同实验设备及测试条件,测试结果本身具有一定误差[6],同时样品本身也可能存在一定尺寸效应[20]。

(1) 通过对完整致密砂岩样品进行常规三轴力学与声学同步测试,获得了含有不同矿物组成的致密砂岩的C、φ值,探讨了基于H-B准则的致密砂岩C、φ值测井解释方法。

(2) 采用方法3对致密砂岩岩样C、φ值进行直接估值计算时,C值并没有偏大,而φ值略微偏低,是实验所施加围压及法向应力较高的缘故。

(3) 提出的基于Hoek-Brown准则的岩石C、φ测井解释方法能较全面考虑到各单因素对岩石抗剪强度参数的影响,评价效果较好,扩展了岩石C、φ值获取的途径。

(4) 提出基于Hoek-Brown准则的致密砂岩抗剪强度参数测井解释方法,利用该方法对地层岩石C、φ值进行测井解释。

(5) 优选单轴参数法对单井致密砂岩目的层C和φ进行测井解释,解释结果与地层实际情况及岩样C、φ实测结果间均具有较好的一致性,表明本文所提出方法的有效性及实用性。对于不同类型岩石,当已知条件或参数有限时,可以选择适当方法对岩石抗剪强度参数进行测井解释。

参考文献:

[1] Christopher P Bobko, Benjamin Gathier, J Alberto Ortega, et al. The Nanogranular Origin of Friction and Cohesion in Shale: A Strength Homogenization Approach to Interpretation of Nanoindentation Results [J]. Int J Numer, Anal Meth Geomech, 2011, 35: 1854-1876.

[2] Anderson O L. Stress Corrosion Theory of Crack Propagation with Application to Geophysics [J]. Review of Geophysics and Space Physics, 1977, 159(1): 77-90.

[3] 尹帅, 单钰铭, 周文, 等. Hoek-Brown准则在岩石抗压强度测井解释中的应用 [J]. 桂林理工大学学报, 2014, 34(4): 659-664.

[4] F Leo Lynch, Lawrence E Mack, Lynton S Land. Burial Diagenesis of Illite/Smectite in Shales and the Origins of Authigenic Quartz and Secondary Porosity in Sandstones [J]. Geochimica et Cosmochimica Acta, 61(10): 1995-2005.

[5] 王学滨, 杜亚志, 潘一山, 等. 弹性-脆性-损伤模型及其在岩石局部破坏研究中的应用 [J]. 应用基础与工程科学学报, 2012, 20(4): 642-651.

[6] 宋彦辉, 巨广宏. 基于原位试验和规范的岩体抗剪强度与Hoek-Brown准则估值比较 [J]. 岩石力学与工程学报, 2012, 31(5): 1000-1006.

[7] Walid M Mabrouk. Acoustic Impedance Inversion Approach from Petrophysical Data [J]. Journal of Petroleum Science and Engineering, 2010(73): 181-184.

[8] 夏开宗, 陈从新, 刘秀敏, 等. 基于岩体波速的Hoek-Brown准则预测岩体力学参数方法及工程应用 [J]. 岩石力学与工程学报, 2013, 32(7): 1458-1465.

[9] Erik Eberhardt. The Hoek-Brown Failure Criterion [J]. Rock Mech Rock Eng, 2012(45): 981-988.

[10] Rousseeuw P J. Robust Estimation and Identifying Outliers in Wadsworth HM (ed) Handbook of Statistical Method for Engineers and Scientists [M]. New York: McGraw-Hill, 1998: 238-243.

[11] 闫长斌, 徐国元. 对Hoek-Brown公式的改进及其工程应用 [J]. 岩石力学与工程学报, 2005, 24(22): 4030-4035.

[12] 宋建波, 于远忠. 岩体经验强度准则及其强度参数m,s的确定方法 [J]. 西南工学院学报, 2001, 16(1): 26-29.

[13] Hoek E. Practical Rock Engineering [M]. E-book, 2007.

[14] 李彦军, 王学武, 冯学钢, 等. T3x须家河组砂岩饱水作用下水岩相互作用规律研究 [J]. 水土保持研究, 2008, 15(3): 226-228.

[15] 尹帅, 单钰铭, 周文, 等. Hoek-Brown准则在致密砂岩弹性参数测井解释中的应用 [J]. 石油钻探技术, 2015, 43(1): 88-95.

[16] 钟作武, 陈汉珍, 周密. 砂岩结构面抗剪强度参数研究 [J]. 地下空间与工程学报, 2006, 2(8): 1383-1386.

[17] 伍章健. 复合材料界面和界面力学 [J]. 应用基础与工程科学学报, 1995, 3(3): 302-309.

[18] 周延军, 耿应春, 王贵宾, 等. 深部地层岩石力学性质测试与分析研究 [J]. 岩土力学, 2011, 32(6): 1625-1630.

[19] Wang Yimin, Chen Yekai, Liu Wei. Large-scale Direct Shear Testing of Geocell Reinforced Soil [J]. J Cent South Univ Technol, 2008, 15: 895-900.

[20] 黄曼, 杜时贵, 罗战友, 等. 基于多尺度直剪试验的岩石模型结构面抗剪强度特征研究 [J]. 岩土力学, 2013, 34(11): 3180-3185.