基于格子Boltzmann方法的3D数字岩心渗流特征分析

张思勤, 汪志明, 洪凯, 程青松, 曾泉树, 赵岩龙, 郭肖

(1.中石化石油工程机械有限公司第四机械厂, 湖北 荆州 434022; 2.中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249; 3.中国石油南方石油勘探开发有限责任公司, 广东 广州 510240;4.中国石油天然气股份有限公司塔里木油田分公司, 新疆 库尔勒 841000)

0 引 言

与国外相比,中国页岩气储层物性差、各向异性突出,孔隙结构存在多尺度特性。对页岩气储层进行渗流行为模拟时达西定律不再适用,常规的解析方法也较难对其渗流性质进行准确模拟[1-4]。此外,由于其孔隙结构的多尺度性和组分的复杂性,较难对其物性参数进行定量描述,提出一种微观图像构建数字岩心与Image J软件[5-6]相结合的方法定量提取孔隙信息。采用MATLAB图像处理技术和Image J软件对页岩二维切片图像进行处理,根据所提取的孔隙结构信息重建页岩气储层的三维数字岩心,然后采格子Boltzmann方法[7-8]对所建的三维数字岩心进行渗流行为的模拟,并分析孔隙结构对渗透率的影响。

1 格子Boltzmann方法

格子Boltzmann方法是一种新的模拟流体的方法,其模型主要包含流体粒子的离散速度集合、格子结构和演化方程3个要素。它描述了具有离散速度的流体粒子分布函数在1个固定格点上的运动过程。

粒子分布函数fi(x,t)的时间演化方程为

(1)

式中,fi(x,t)表示在时刻t、位置x处的节点上第i个方向的粒子分布函数;x是格子上的一个格点;{ci:i=1,2,…,b}是流体粒子的离散速度集合;δt是离散时间步长;t为当前时间步;τ为松弛时间。分布函数的演化过程主要分为碰撞和传播2步,在碰撞过程中,通过每个格点的质量和动量重新分布;在传播过程中,粒子向邻近点流动。

本文采用的格子模型为D3Q19模型,构造格子Boltzmann模型的关键在于选取合适的平衡态分布函数,离散速度的个数太少可能导致某些物理量不满足守恒定律,离散速度的个数太多又会造成计算上的浪费,D3Q19模型其平衡态分布函数

(2)

(3)

D3Q19模型(见图1)的速度配置为

(4)

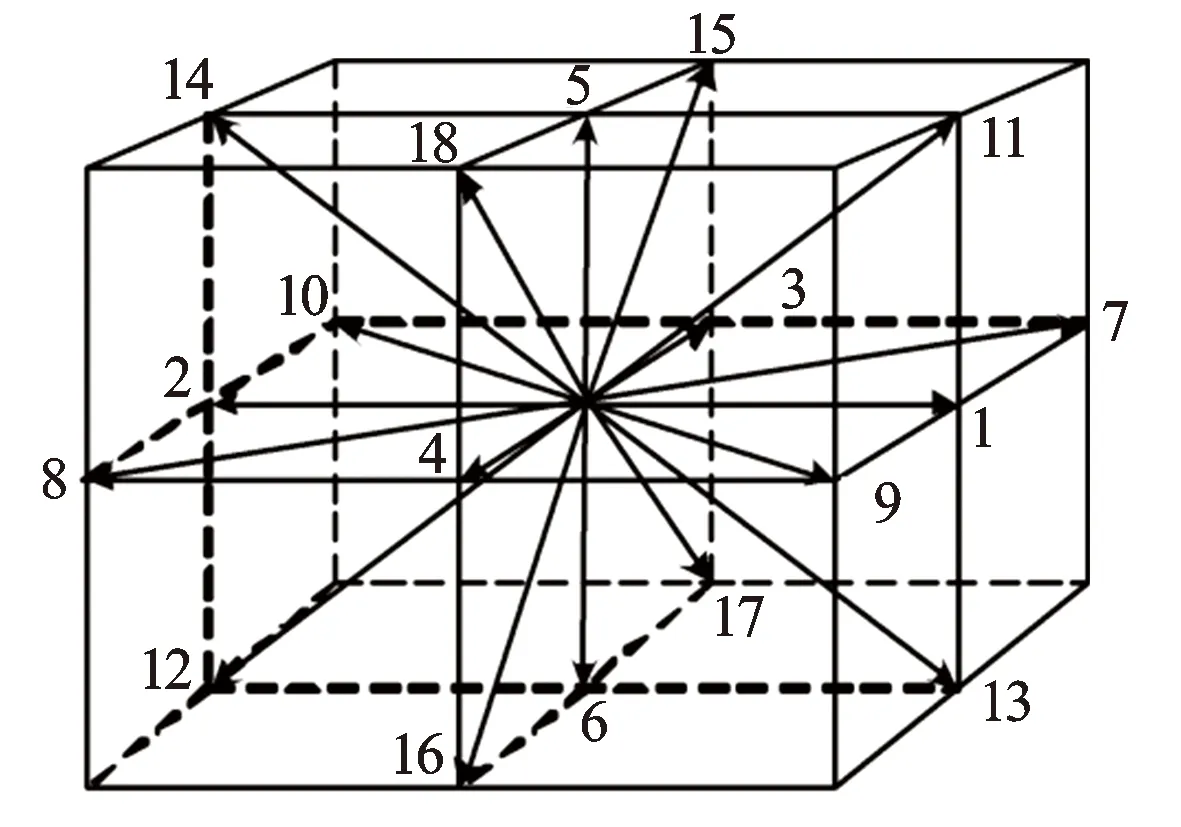
图1 D3Q19格子模型示意图

根据质量守恒定律和动量守恒定律原则,可以得到宏观物理参数与微观粒子分布函数的关系式

(5)

(6)

(7)

(8)

2 数字岩心重建

通过MATLAB图像处理技术对页岩气储层二维岩心切片进行阈值分割和二值化处理,得到岩心切片的二值化图像;采用Image J软件对二值图像进行信息提取,得到孔隙分布个数及其半径大小。根据所提取的孔隙信息将按孔隙半径划分为2个孔隙,小于1 μm的为小孔隙,大于1 μm的为大孔隙。以此为基础在切片图像中选择具有代表性的一部分大孔隙和小孔隙进行三维数字岩心的重建。

2.1 页岩气储层信息提取

重建三维数字岩心需要3张相互垂直的独立的二维图像。采用四参数随机生长方法,故只需要1张页岩气储层二维切片图像即可;页岩储层二维岩心切片取自数字岩心物理实验室(见图2)。

图2 页岩SEM图像与二值图像

在图2中选取具有代表性的一部分大孔隙和小孔隙用于重建三维数字岩心的基础图像,应用MATLAB计算机图像处理技术对图像进行处理,并对图像孔隙结构特征进行分析和统计,其结果见表1。

表1 页岩孔隙结构参数

将表征单元体作为选择岩体介质类型的依据,表征单元体是指多孔介质的一个控制体积,它包含足够多的微小孔隙,尺寸远大于单个孔的尺寸,但又远小于宏观流动区域的尺度,故相比于宏观渗流区域,REV可以看成是一个点。其概念类似于流体连续介质假定中流体质点的概念。以大孔隙页岩切片图像对页岩REV进行说明,图3(右)为采用四参数随机方法重建的页岩切片图像。图4为页岩切片重建图像与原图自相关函数和变差函数对比图。重建图像与原图的自相关函数和变差函数吻合性较好,验证了四参数随机方法的可行性。自相关函数图中,当测量单元尺寸L>20时就能满足条件。故在后期重建过程中取L=50。

图3 大孔隙页岩岩心切片重构图像与原图对比图

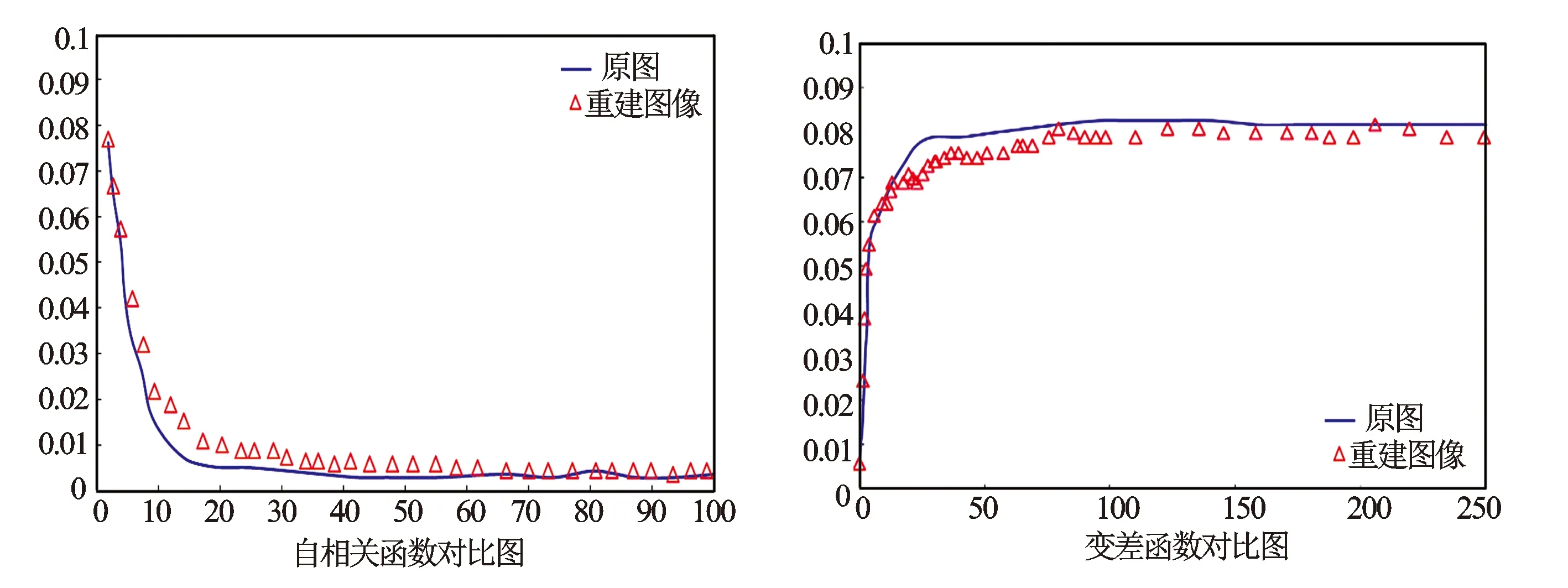
图4 页岩切片自相关函数与变差函数对比图

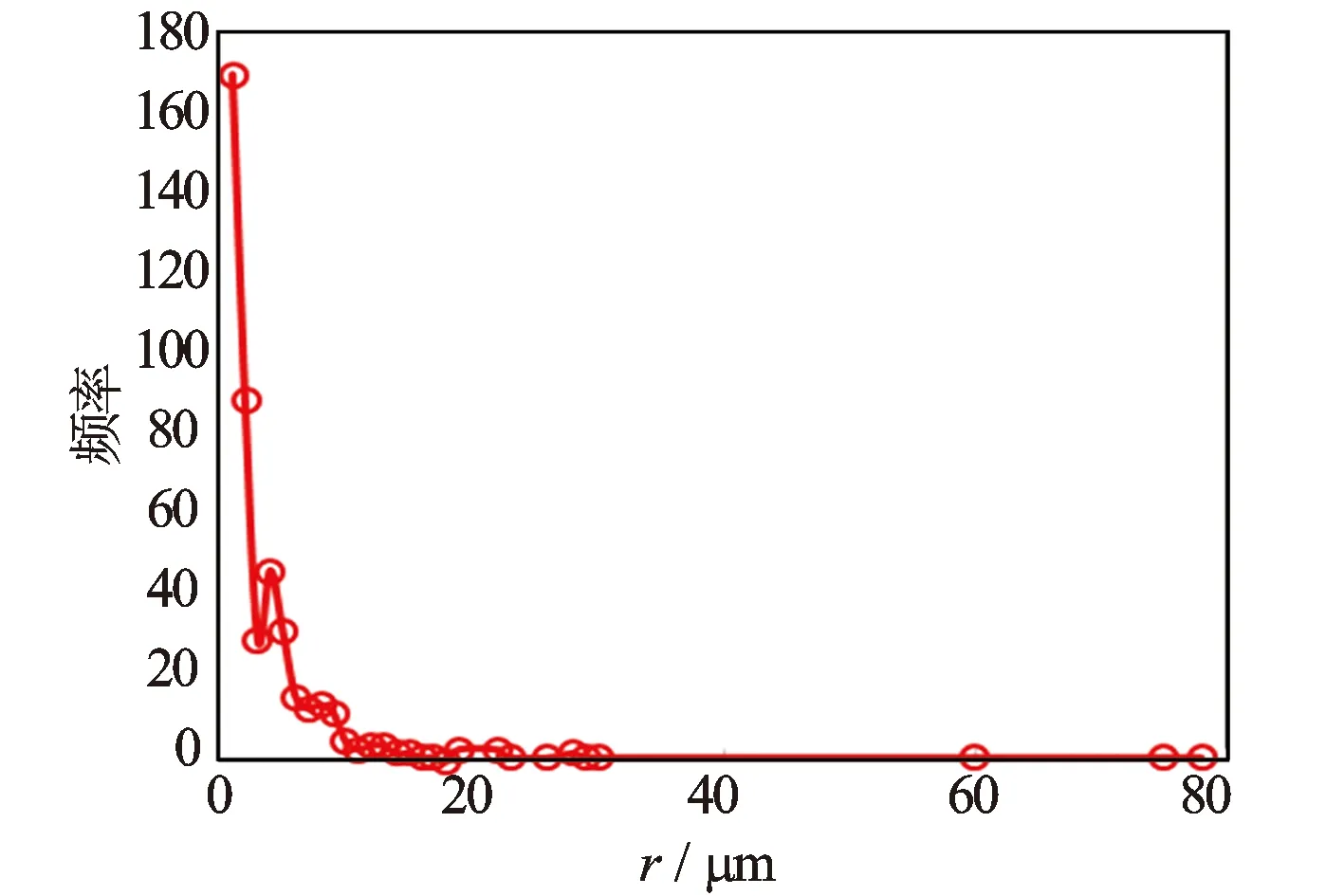
图5 页岩数字岩心的孔隙半径频率分布

图5为页岩切片图像的孔隙半径频率分布图。图6是2种对孔隙大小的划分标准,一种是Choquette and Pray于1970将孔隙划分为5种基本类型;另一种是Loucks等2012年将孔隙划分为3种基本类型。总图像中孔隙主要以纳米孔隙和微孔隙为主,中孔和大孔较少。以2种不同孔隙重建数字岩心。

图6 孔隙尺寸划分方法

2.2 重建方法

建立三维数字岩心的方法分为物理实验方法和数值重建方法两大类,物理实验方法重构的三维图像效果较好,但其价格昂贵,不便于大规模使用,数值重建方法一般是以1张或数张二维切片图像为基础结合一定的数学方法重建数字岩心。要对所建的页岩气储层数字岩心采用格子Boltzmann方法进行流动模拟,采用与格子Boltzmann方法紧密结合的四参数随机生长方法建立页岩气储层的三维数字岩心。

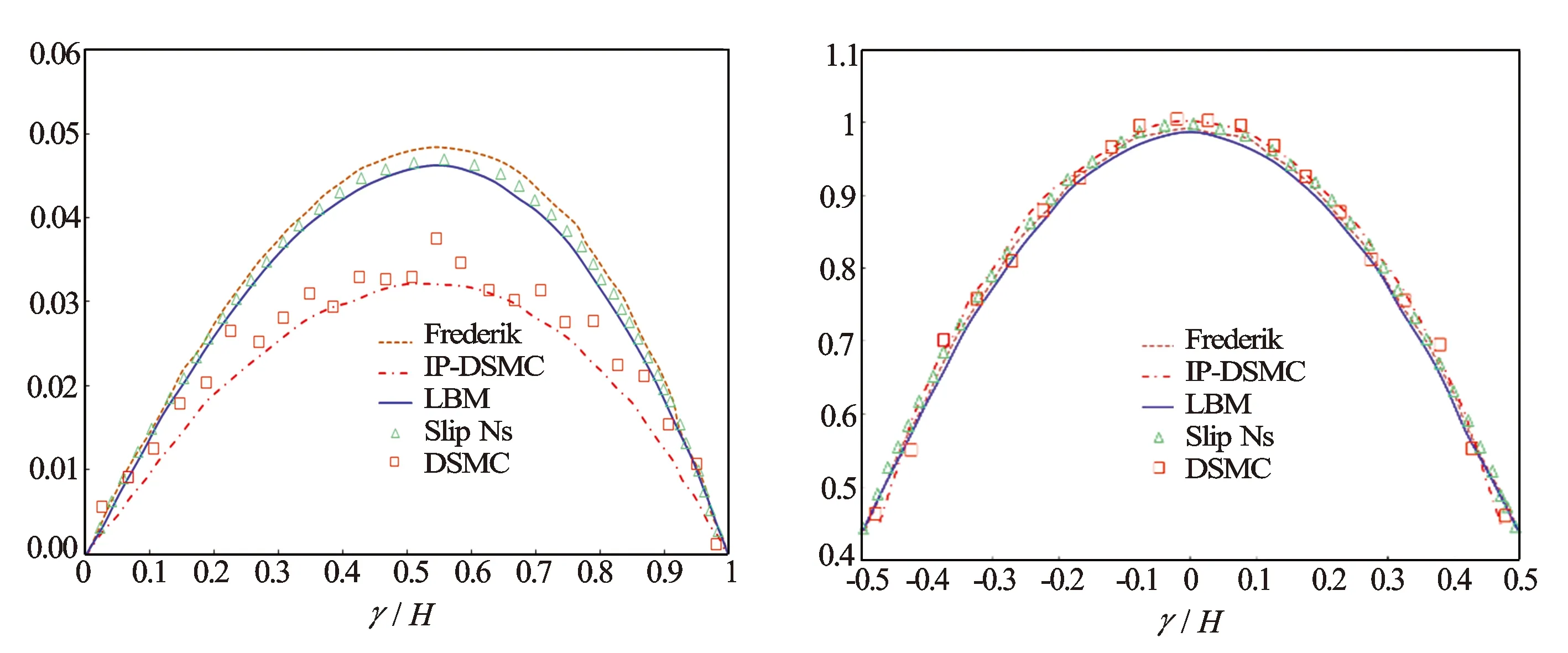
图7 压力分布偏差与出口端速度剖面(Kn=0.194)

采用四参数随机生长法(Quartet Structure Generation Set, QSGS)构造多孔介质微观REV结构[9-10]。首先建立孔隙和基质的三维多孔介质,令基质为生长相,孔隙为非生长相,初始相全为孔隙。

(1) 在构造网格上以概率pc1随机布置第1个生长相的生长核,pc1要小于该相的体积分数。

(2) 对于每一个生长核,按照不同方向上给定的生长概率pi生长,即第i个方向的相邻单元的状态以概率pi变为第1相态(i=1,2,…,18)。

(3) 重复步骤2,直至非生长相(孔隙)达到给定的孔隙率n。

(4) 最后,网格中没有被生长相占据的位置即为非生长相单元。

2.3 重建的3D数字岩心

采用随机生长方法得到小孔隙三维数字岩心,再用四参数随机生长方法重建大孔隙三维数字岩心,基于所建立的大孔隙和小孔隙三维数字岩心为基础,进行模型的组合。组合表达式为

Π=Π1+Π2

(9)

式中,Π为总模型中参数;Π1为大孔隙模型中参数;Π2为小孔隙模型中参数。大孔隙和小孔隙的基础模型中,均只包含基质和孔隙2部分,其组合类型有4种。

(10)

在组合过程中,先放进模型的组分会有部分被后放进去的所覆盖,在实际建模过程中,结合各组分的特点,根据各种组分的重要性,设定优先级。在组合过程中,设定孔隙度的优先级高于基质,即孔隙度后组合到总模型中,组合完成后,得到的三维数字岩心。

3 页岩气储层微观流动模拟

3.1 模型验证

选取单孔隙通道对LBM模型进行验证,采用D2Q9模型模拟二维圆管Poiseuille流动。页岩气储层孔隙小,其渗流行为属于微尺度流动[11-12],对于微尺度流动要解决2个基本问题:一是确定松弛时间和Knudsen数之间的关系;另一个是微尺度流动的边界条件处理。引入Knudsen数与松弛时间的关系式

(11)

通过引入Knudsen数,使格子Boltzmann方法模拟微尺度流动成为可能。考虑到气体的压缩性,对松弛参数进一步修正,采用Nie等提出的修正松弛参数τ,其修正表达式

(12)

图7给出了在Kn=0.388情况下微通道中心处压力分布偏差和出口端速度分布。通过与Frederik、IP-DSMC、Slip NS、DSMC等的模拟结果进行对比分析,发现模拟结果与Frederik模拟结果和Slip NS的结果符合性较好,但与IP-DSMC和DSMC等的模拟结果有一定的偏差。分析原因主要是当Kn=0.388时,此时的流动为弱过渡流,采用的是单精度的模型,需要引进更加复杂精度的模型。在研究的Kn数范围内,该精度的模型模拟的结果还是有效的,在一定程度上验证了模型和方法的准确性。

3.2 页岩气储层数字岩心渗流特性模拟

采用格子Boltzmann方法对3种不同类型的页岩气储层数字岩心的孔隙度和渗透率进行模拟计算,选取D3Q19模型,出入口边界采用压力边界,初始格子速度都为0,初始格子密度都为0,可用格子Boltzmann方法计算所建数字岩心的固有渗透率[13-15],重构页岩储层三维数字岩心的孔隙度和渗透率结果见表2。随着孔隙度增大,所重建数字岩心的渗透率明显增大,组合模型的渗透率不仅分别大于大孔隙数字岩心的渗透率和小孔隙数字岩心的渗透率,而且远大于两者总和,这说明小孔隙的存在可以大大地提高数字岩心的连通性,可以极大地提高整体数字岩心的渗透率。

(13)

式中,K为格子渗透率;N为孔隙空间的格子总数;n为格子方向,此时n=18。

孔隙度的计算式为

(14)

表2 数字岩心物性参数与模拟结果对比

4 结 论

(1) 随机生长方法重建数字岩心过程简单、成本低,只需要1张二维切片图像,且与其他重建方法相比,采用随机生长方法和组合法配合重建数字岩心能够极大地提高计算效率。

(2) 通过MATLAB图像处理技术和Image J软件配合,统计出页岩气储层孔隙主要以纳米孔和微米孔为主,通过对自相关函数和变差函数分析,发现四参数随机方法重建图像能较好反映原图性质。

(3) 渗透率随孔隙度的增大而增大,且组合数字岩心的渗透率分别大于大孔隙数字岩心和小孔隙数字岩心的渗透率,且远大于二者的总和,小孔隙的存在可以极大地提高储层的连通性。

参考文献:

[1] 李建忠, 董大忠, 陈更生, 等. 中国页岩气资源前景与战略地位 [J]. 天然气工业, 2009(5): 11-16, 134.

[2] 陈尚斌, 朱炎铭, 王红岩, 等. 中国页岩气研究现状与发展趋势 [J]. 石油学报, 2010(4): 689-694.

[3] 张小涛, 吴建发, 冯曦, 等. 页岩气藏水平井分段压裂渗流特征数值模拟 [J]. 天然气工业, 2013(3): 47-52.

[4] 段永刚, 李建秋. 页岩气无限导流压裂井压力动态分析 [J]. 天然气工业, 2010(10): 26-29, 116.

[5] 王银改. Image J软件在检验医学图像分析处理中的应用 [J]. 中华检验医学杂志2005, 28(7), 747-748.

[6] 徐祖新, 郭少斌. 基于氩离子抛光-SEM和ImageJ软件的页岩储层孔隙结构分析——以中扬子地区陡山沱组为例 [J]. 大庆石油学院学报, 2014(4): 45-51.

[7] 何雅玲, 王勇, 李庆. 格子Boltzmann方法的理论及应用 [M]. 北京: 科学出版社, 2009.

[8] 郭照立, 郑楚光. 格子Boltzmann方法的原理及应用 [M]. 北京: 科学出版社, 2008.

[9] 李仁民, 刘松玉, 方磊, 等. 采用随机生长四参数生成法构造黏土微观结构 [J]. 浙江大学学报: 工学版, 2010, 44(10): 1897-1901.

[10] Wang M, Wang J, Pan N, et al. Mesoscopic Predictions of the Effective Thermal Conductivity for Micro-scale Random Porous Media [J]. Phys Rev E 75, 036702, 2007.

[13] Chai Zhenhua, Guo Zhaoli, Shi Baochang, et al. Predictionof Permeability in Porous Media with Multi-relaxation-time Lattice Boltzmann Method [J]. Journal of Engineering Thermo Physics, 2010, 31(1): 107-109.

[14] 朱益华, 陶果, 方伟, 等. 3D多孔介质渗透率的格子Boltzmann模拟 [J]. 测井技术, 2008, 32(1): 25-28.