基于MPC编码方式的软件产品线配置优化算法研究

郑炜, 曹立鑫, 李隆俊, 李宁

(1.西北工业大学 软件与微电子学院, 陕西 西安　710072；2.西北工业大学 计算机学院, 陕西 西安　710072)



基于MPC编码方式的软件产品线配置优化算法研究

郑炜1, 曹立鑫1, 李隆俊1, 李宁2

(1.西北工业大学 软件与微电子学院, 陕西 西安710072；2.西北工业大学 计算机学院, 陕西 西安710072)

摘要：软件产品线配置问题是一个多目标选择难题，借助于遗传算法的全局搜索能力可以得到成本低、耗时少、功能健全的最优方案解。合理的软件产品线特征模型映射编码可以提高求解效率，增加有效解的个数。传统的直接编码是对所有特征进行编码，这使得大型软件产品线配置问题求解效率低下，并且往往得到无效解。现行的强制编码通过隐藏强制节点来缩小特征编码范围，从而达到提高求解效率的目的。然而，很多大型软件产品线配置问题依然未得到有效解决。针对这一问题，提出一种新型编码方式——MPC编码，在强制编码的基础上，通过节点子父关系进一步缩小编码范围，更加有效提高求解效率，从而获取最优方案解。最后通过传统模型与随机模型进行编码方式验证，将MPC编码与直接编码以及强制编码进行对比，证明MPC编码在求解软件产品线配置问题中的有效性。

关键词：软件产品线;软件配置;多目标优化;遗传算法;特征模型;编码方式

软件产品线是一组具有共同体系构架和可复用组件的软件系统，它们共同构建支持特定领域内产品开发的软件平台。软件产品线集中体现一种大规模、大粒度软件复用实践，是软件工程领域中软件体系结构和软件重用技术发展的结果[1]。软件产品线特征建模是呈现组件模块之间依赖、互斥等关系的重要手段，自Kang等[2]在1990年介绍面向特征域的分析方法提出后，特征建模就被广泛运用于软件产品线中。合理的配置特征模型直接影响和决定了整个产品线的质量和成败，然而产品线配置解决方案域并不唯一，因此如何获取最优配置方案解变得尤为重要。

遗传算法是一种求解问题的高度并行性全局搜索算法，它能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最优解，因此它在多目标优化问题的优化求解中有很大的作用和优势[3]。现阶段研究表明，将软件产品线特征模型映射编码后，通过遗传算法可以有效得到最优配置方案解[4]。本文将对现有的编码方式予以改进，通过合并相互依赖性高的模块，进一步合理缩小软件产品线特征模型，从而提高获取最优方案解的效率与个数。经过大量实验证明，这种编码方式是有效的。

1软件产品线介绍

1.1特征模型

软件产品线工程是一个系统的发展软件系列产品的方法[5]，其中软件产品被定义为一个特征集合，一个特征就代表着产品的一项功能。特征模型通常被用来表示一个软件产品线中的全部产品[2]，特征模型可以表示为可见的树状结构，树的节点表示特征，树状结构将特征节点相关联。只要遵循特征模型的依赖、互斥等关系进行配置，就可以得到一个有效的软件产品配置。例如，图1为GPS(全球定位系统)的特征模型，其根节点特征为GPS产品线本身。根据父节点与子节点之间的关系，其他节点可分为以下几种类型：

1)强制型定义该节点为其父节点必要节点，标示为●。如图1中，寻路系统及人机交互是GPS产品线必须实现的功能，屏幕是人机交互必须具备的配置。

2)可选型定义该节点为其父节点的可选节点，标示为○。如图1中，提供路况信息是GPS产品线的可选功能。

3)组间或类型定义为其父节点有且仅有一个子节点，标示为g[1,1]。如图1中，屏幕必须在触摸屏与液晶显示器中二选一。

4)组间异或类型定义为其父节点至少有一个子节点，标示为g[1,*]。如图1中，寻路系统在3D地图与自动寻路中至少实现一个功能。

此外，特征之间还存在2种约束关系：

1)等价关系选择特征A则并需选择特征B，表示为单箭头虚线。如图1中，路况信息与自动寻路为等价关系。

2)互斥关系特征A与特征B不能同时存在，表示为双箭头虚线。如图1中，键盘与触摸屏为互斥关系。

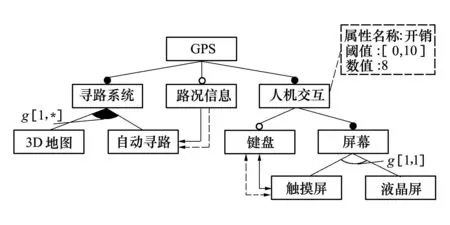
图1　GPS特征模型

与此同时，特征模型通过特征属性来扩展特征的额外信息。特征属性的组成通常为：属性名称、阈值与数值。如图1中人机交互的一个属性，可知其开销为8。特征属性不仅用来统计整个产品的细节信息，更是合理配置产品功能的重要依据。

1.2多目标优化

软件产品线最优化问题主要包含2类目标函数：①尽可能少的成本开销；②尽完备的实现功能。此问题也被称为多目标优化问题，多目标优化旨在找出一组同时满足所有优化目标的解集，再由相关决策做出最终选择。传统的多目标优化问题解决方案主要有2个：①将多目标转换为单目标，即把各目标加权，然后选择权值最高的解作为最优解；②仅针对多目标中的某一目标求解，其他目标只需达到一定范围即可。

然而，传统的多目标优化具有很大的主观性、不一致性，并不能有效的得到最优方案解。通过遗传算法可以很好解决这些问题，遗传算法可以并行的处理一组可行的解集，能在一次运算过程中找到满足多个目标的Pareto最优解集。

2新型的编码方式

软件产品线编码方式是将其特征模型依照特征进行编码，使它的排列形式符合遗传算法的基因序列，随后根据特征属性进行选择运算，最终获得软件产品配置最优方案解集。优秀的编码策略能极大的提高获取最优方案解集的效率和个数，文章将介绍三种编码方式：直接编码方式，强制编码，以及一种新型的编码方式——MPC编码。

2.1直接编码

直接编码即为直接按照层次遍历顺序对特征树进行编码。令特征集为S，编码特征集为S′，则S′=S。例如，图2为任意特征模型树，此特征模型的直接编码如图3所示。

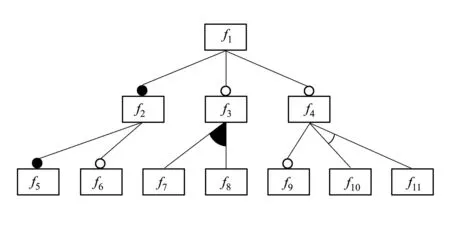
图2　特征模型树

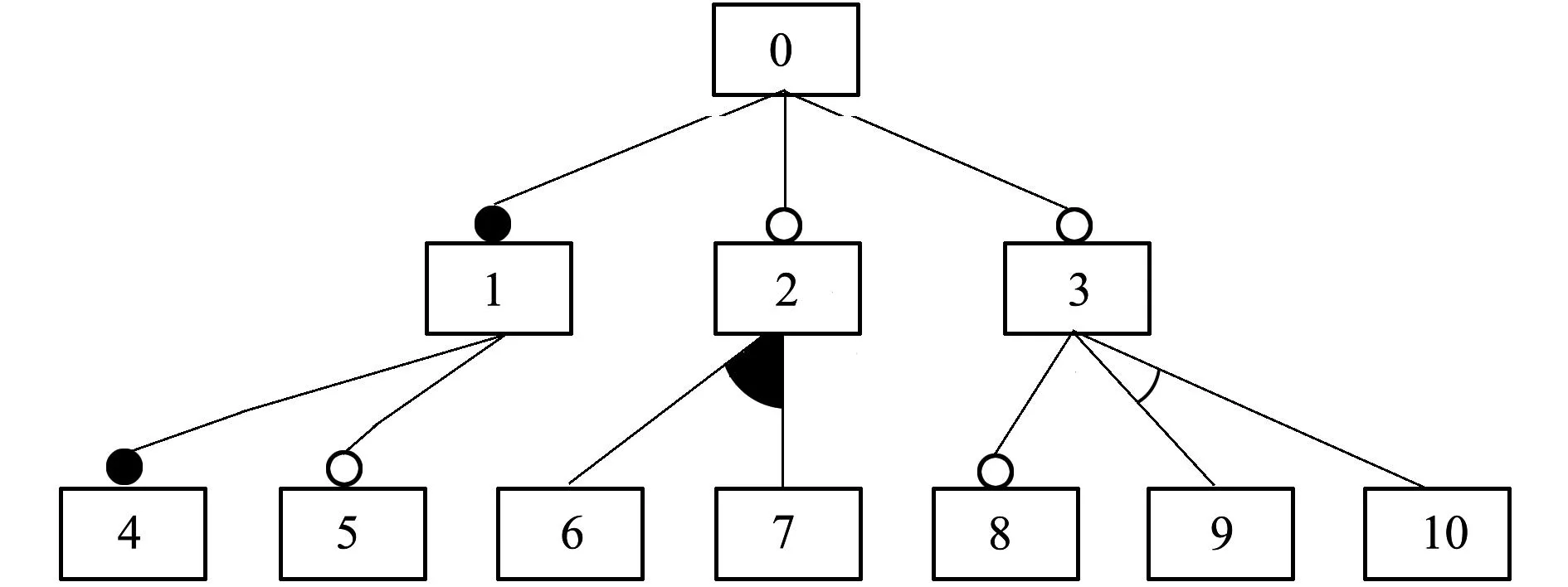
图3　直接编码

2.2强制编码

强制编码是将强制型节点和其父节点结合为1个特征节点的编码方式。令特征集为S，编码特征集为S′，强制型节点集为M，则S′=S-M。例如，在图2中，f1存在时f2必定存在，f2存在时f5必定存在，因此f1、f2与f5是共存的，于是可将3个特征结合为1个特征再依照层次遍历进行编码，如图4所示，从而达到减小模型编码序列的目的，提高求解配置最优解的效率。

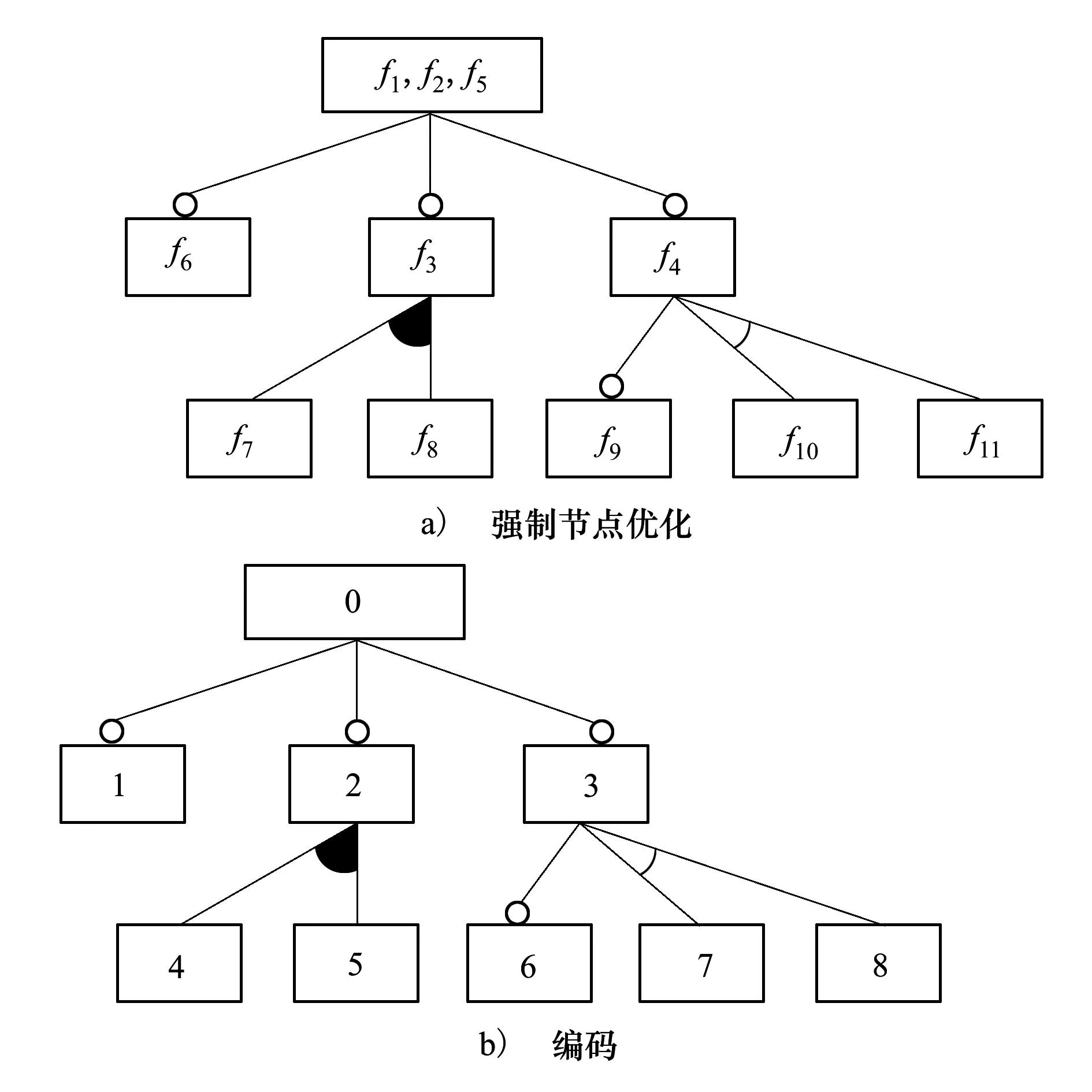
图4　强制编码

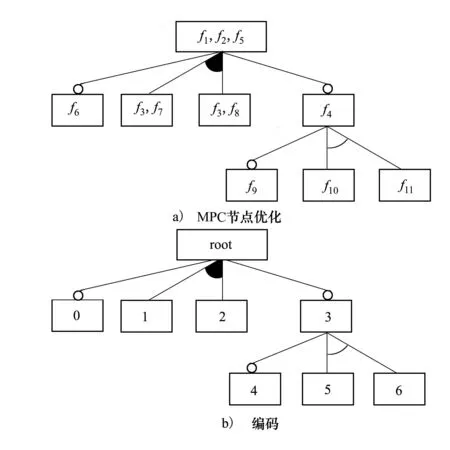
图5　MPC编码

2.3MPC编码

MPC编码又称强制子父节点编码，是基于强制编码改进的编码方式，通过隐藏子父关系节点达到进一步缩小编码范围的目的。令特征集为S，编码特征集为S′，强制型节点集为M，根节点为r，组间型节点g的父节点为gf，该父节点gf的非组间型节点为fc，则：

例如，在图2中，f3有且仅有一组异或子节点f7、f8，因此将f3分别与f7、f8相结合，然后将其祖父节点变为父节点，如图5所示。MPC编码进一步减小模型编码序列，大量实验证明，该编码有效提高了求解最优配置解的效率与个数。

3核心算法

文章将采用遗传算法来求解软件产品线最优配置问题，在算法实现上，首先将特征按照顺序排列为一个0、1序列，其中序列第n位对应特征编码号n-1，当序列第n位值为1时，表示第n-1个特征被选中，当序列第n位值为0时，表示第n-1个特征未被选中。其次，若要得到一个合理、可行的产品配置，需要满足以下5个规则：

1)根节点是必要的，即产品线本身必定存在；

2)任意子节点存在时，其父节点必定存在；

3)若某节点存在强制型子节点，则当该节点存在时，其强制型子节点必定存在；

4)若某节点存在组间子节点时，则必须符合组间节点定义；

5)必须符合等价关系与互斥关系。

因此，我们可根据以上5个规则生成1个规则函数，通过算法1来检验特征序列是否满足配置要求。

算法1 规则函数

输入：特征序列

算法步骤：

Step1若根节点为0，违反规则数+1；

Step2若子节点为0，父节点为1，违反规则数+1；

Step3若父节点为1，其强制子节点为0，违反规则数+1；

Step4若父节点为1，其组间异或子节点都为0，违反规则数+1；

Step5若父节点为1，其组间或子节点全部为0或有2个以上为1，违反规则数+1；

Step6若某节点为1，其等价节点为0，违反规则数+1；

Step7若某节点为1，其互斥节点为1，违反规则数+1。

输出：违反规则数。

最终，当得到的违反规则数等于0时，表示当前特征序列满足要求，是一个有效的配置方案解。

4实验配置

4.1遗传算法

文章将选用2种遗传算法来对特征编码方式予以验证：NSGA-II[6](精英保留的非劣排序遗传算法)和IBEA[7](基于指标的遗传算法)。其中，NSGA-II是NSGA[8](非劣排序遗传算法)的改进算法，有效地将NSGA的计算复杂度从O(mN3)降至O(mN2)，从而进一步提高算法的计算效率和鲁棒性。IBEA是一种通用多目标遗传算法，该算法首次将评价指标函数作为适应度评价方法嵌入到遗传算法中，使其可以与任意服从Pareto优胜规则的指标相结合，常用的指标有二元additive epsilon指标和二元hypervolume指标。

4.2SPL特征模型

文章选用2个传统模型E-Shopping[9]和WebPortal[10]，以及2个大数据随机模型来验证3种编码方式，并使用Hypervolume指标(简称HV)来评估运算结果。E-Shopping是一个商务网站模型，WebPortal是一个门户网站模型，2个大数据随机模型分别采用5 000特征节点和10 000特征节点。其中，每个特征模型的基本数据如表1所示。

在实验中，模拟了5个目标来定义特征模型，并赋予初值：

1)违反规则数：通过特征模型树所生成的符合5个规则的规则函数，计算遗传算法个体解违反规则的数量，取最小值；

2)特征个数：个体解中包含特征的个数，取最大值；

3)特征被用性：个体解中的特征是否曾经被使用过，未曾使用过的特征存在未知缺陷，因此取最大值；

4)已知缺陷个数：曾经被使用过的特征都存在已知的缺陷个数，其值取最小值；

5)开销：每个特征都存在开销，其值取最小值。

5实验结果及结论分析

在实验中，首先对4个特征模型进行编码，编码后的节点个数如表2所示。其中，EN表示编码节点个数，OP表示优化概率。优化概率的公式为：令特征个数为f，编码个数为e，则OP=(f-e)/f×100%。通过编码结果不难看出，MPC编码进一步缩小了模型大小，在10 000节点随机模型中可优化比高达40%，使得求解效率得到进一步提高。

表1　特征模型的基本数据

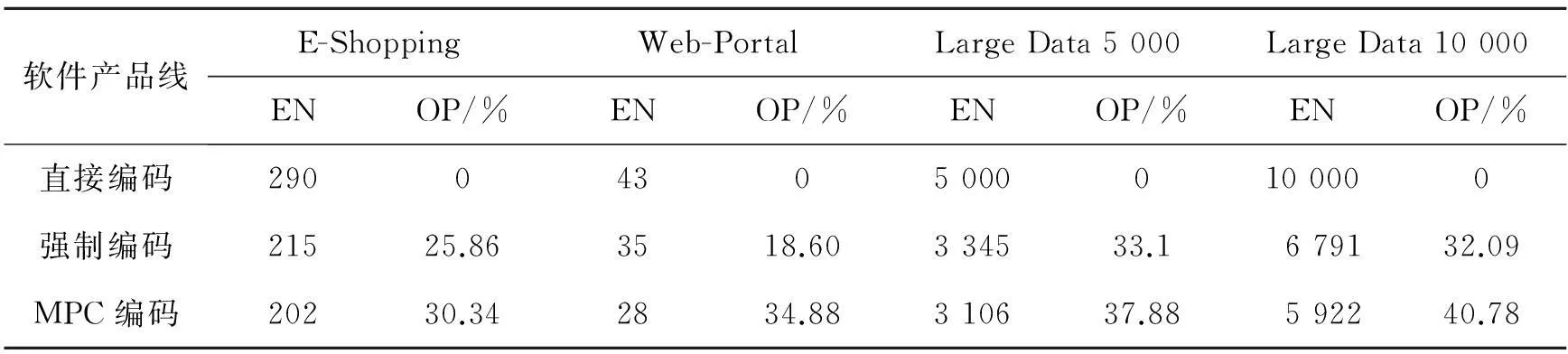
表2　3种编码节点统计

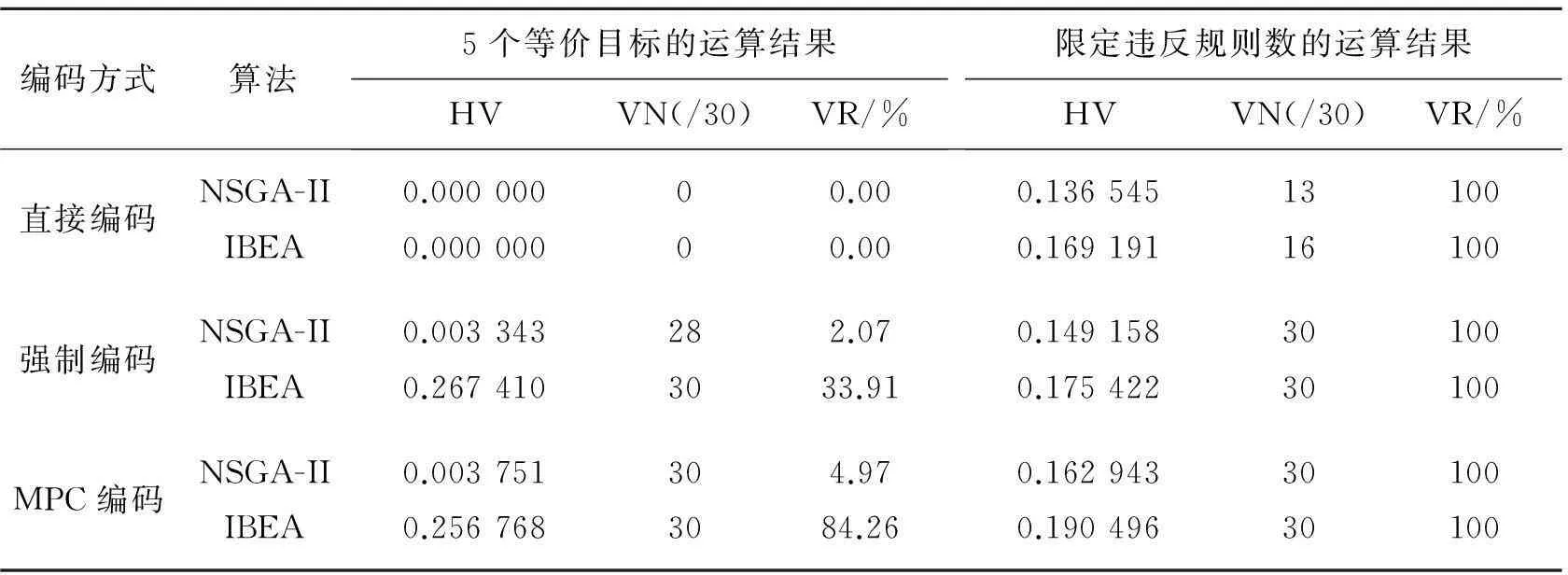
表3　E-Shopping数据测评结果

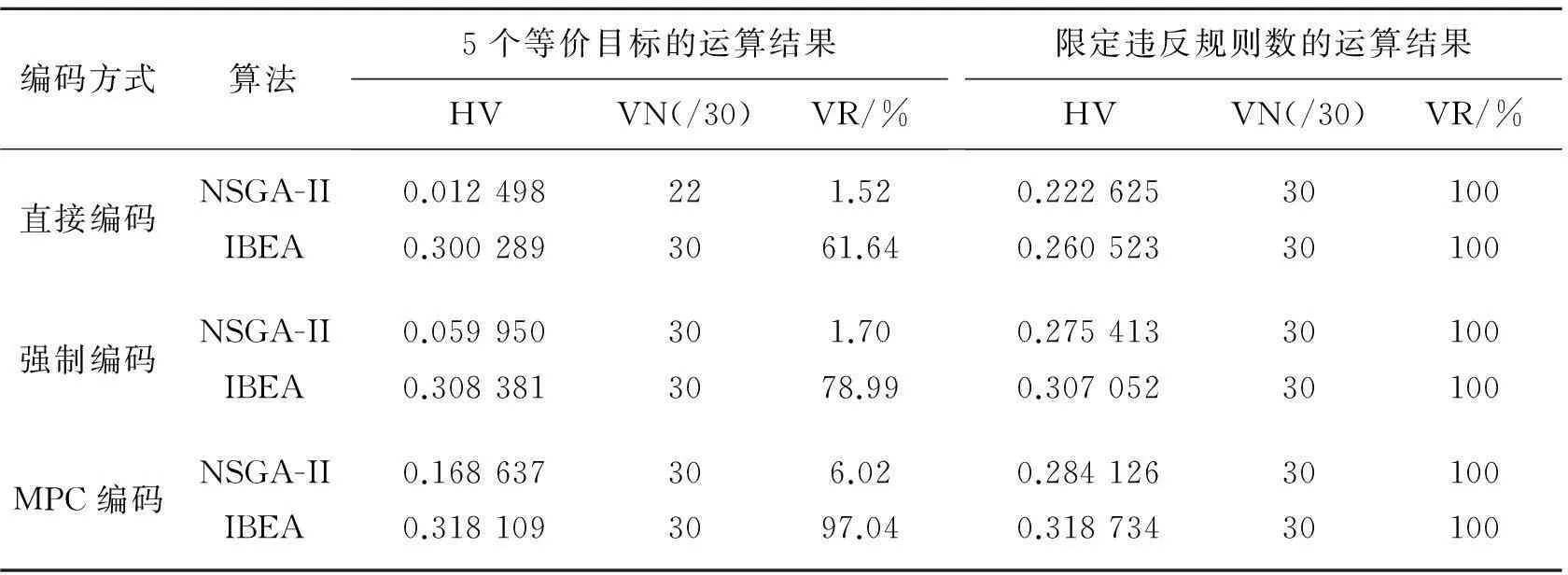
表4　Web-Portal数据测评结果

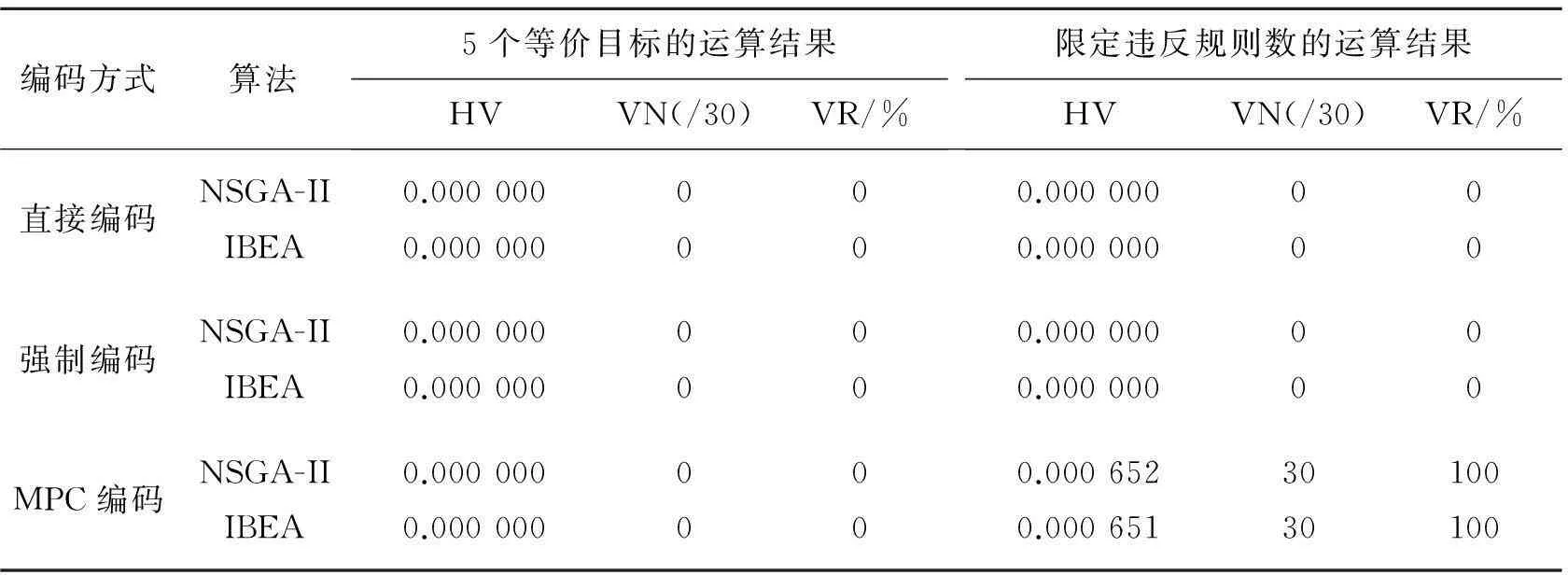
表5　数据5 000节点数据测评结果

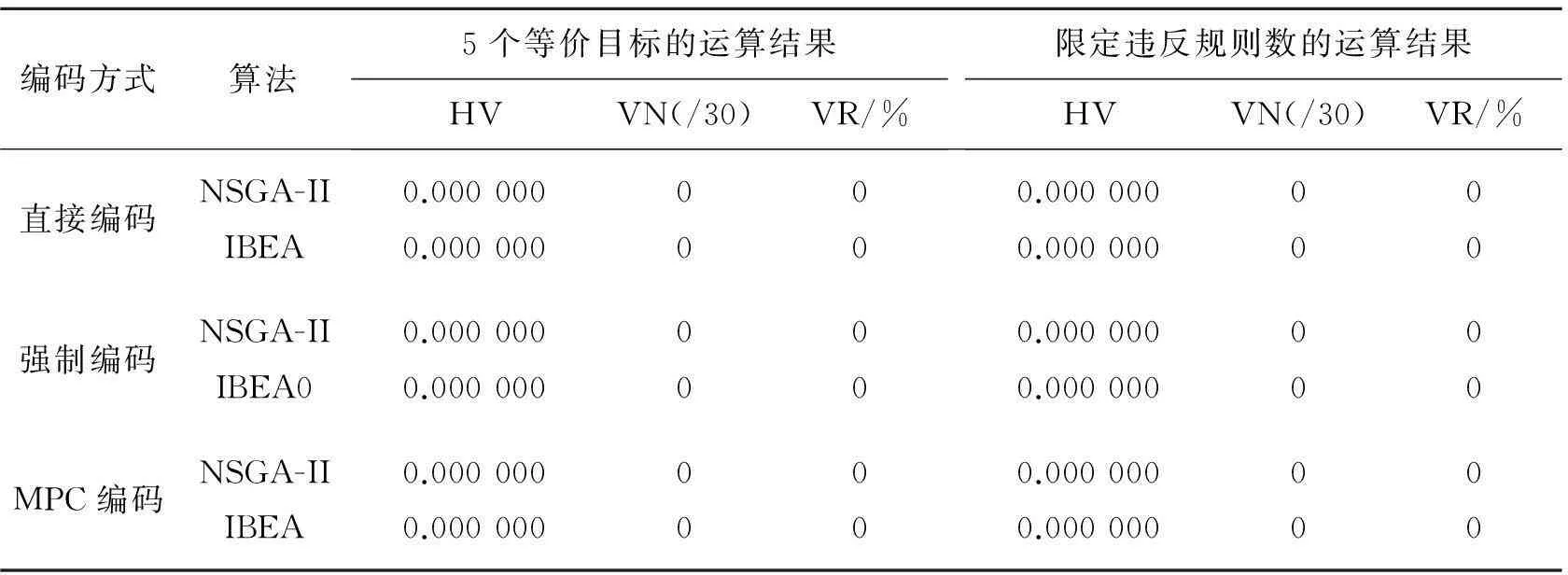
表6　大数据10 000节点数据测评结果

在求解最优方案解中，2个遗传算法分别执行2遍，1遍为5个等价目标的执行，1遍为限定违反规定数为0的执行。每次执行评估50 000次并循环30次，即得到30组解集。表3～表6为4个特征模型的测评结果，其中，VN表示30组解集中含有违反规则数为0解的解集个数，VR表示30组解集中所有违反规则数为0解所占全部解百分比。

比较实验结果可知，在3个编码方式中，MPC编码的HV评估值普遍最优，直接编码的HV评估值通常最低，并且，MPC编码的含有违反规则数为0解的解集个数以及违反规则数为0解所占比也大部分高于其他2个算法。同样地，直接编码普遍偏低。尤其在大型随机模型LargeData实验中，直接编码和强制编码并不能得到有效解，然而MPC编码却得到了有效的结果。由此可证实，MPC编码的确在求解软件配置最优解中更加有效率。

6结论

通过大量实验数据结果可验证MPC编码方式较优于其他编码方式，然而此方法还有很多不足之处。众所周知，软件产品线特征模型是各式各样的，本方法不一定能囊括所有特征模型，在某些特定模型下并不能绝对提高获取最优方案解的效率。如何使MPC编码可以优化更多特征模型是我们进一步研究的问题。

参考文献：

[1]李兰涛, 王忠民. 基于UML的软件产品线建模方法研究[J]. 微计算机信息, 2006, 22(30): 204-206

Li Lantao, Wang Zhongmin. Software Product Lines Modeling Approach with UML[J]. Control & Automation, 2006, 22(30): 204-206 (in Chinese)

[2]Kang K, Cohen S, Hess J, et al. Feature-Oriented Domain Analysis (FODA) Feasibility Study[R]. Technical Report CMU/SEI-90-TR-21, SEI, 1990

[3]Goldberg D E. Genetic Algorithms in Search, Optimization and Machine Learning[M]. Boston, Addison-Wesley Professional,

1989

[4]Abdel Salam Sayyad, Tim Menzies, Hany Ammar. On the Value of User Preferences in Search-Based Software Engineering: A Case Study in Software Product Lines[C]∥35th International Conference on Software Engineering, 2013: 492-501

[5]Clements P, Northrop L. Software Product Lines: Practices and Patterns[M]. Boston, Addison-Wesley Professional, 2001

[6]Kalyanmoy Deb, AmritPratap, Sameer Agarwal, et al. A Fast and Elitist Multi-Objective Genetic Algorithm: NSGA-II[J]. IEEE Trans on Evolutionary Computation, 2002, 6(2): 182-197

[7]Zitzler E, Künzli S. Indicator-Based Selection in Multi-Objective Search[C]∥Proc of the 8th hat′1 Conf Oil Parallel Problem Solving from Nature, 2004

[8]Srinivas N, Kalyanmoy Deb. Multi-Objective Optimization Using Ondominated Sorting in Genetic Algorithms[J]. Evolutionary Computation, 1994, 2(3): 221-248

[9]Sean Quan Lau. Domain Analysis of E-Commerce Systems Using Feature-Based Model Templates[D]. University of Waterloo,

2006

[10] Marcilio Mendonca, Thiago Tonelli Bartolomei, Donald Cowan. Decision-Making Coordination in Collaborative Product Configuration[C]∥Proceedings of the 23rd Annual ACM Symposium on Applied Computing, 2008: 108-113

A New Solution of Configuration Based Genetic Algorithm for Software Product Line

Zheng Wei1, Cao Lixin1, Li Longjun1, Li Ning2

(1．Department of Software Engineering，Northwestern Polytechnical University，Xi'an 710072，China 2．Department of Computer Science and Engineering，Northwestern Polytechnical University，Xi'an 710072，China)

Abstract:A problem, the configuration of software product line, is a puzzle of multi-objective optimization. Optimum solution can be accessed effectively by the capability of searching the optimal solution within defined space form genetic algorithm. Reasonable code of software product line feature model can promote efficiency of global searching and increase the number of efficient solutions. This paper improves current code and obtains a new one - Mandatory Parent Child Encoding. A great number of experimental data indicate that this method is feasible.

Keywords:computational efficiency, cost reduction, genetic algorithms, global positioning system, multi-objective optimization, stochastic models; encoding mode, feature model, MPC(Mandatory Parent Child) encoding, software configuration, software product line

中图分类号：TP311.5

文献标志码：A

文章编号:1000-2758(2016)01-0176-07

作者简介：郑炜(1975—)，西北工业大学副教授，主要从事软件工程及软件测试的研究。

基金项目：国家自然科学基金(61402370)与中央高校基本科研业务费专项资金资助

收稿日期：2015-09-12