绳系卫星释放阶段的空间姿态非线性稳定控制

王长青, 杜崇刚, 李爱军, Z.H.Zhu

(1.西北工业大学, 陕西 西安　710072; 2.York University, Toronto M3J 1P3)



绳系卫星释放阶段的空间姿态非线性稳定控制

王长青1, 杜崇刚1, 李爱军1, Z.H.Zhu2

(1.西北工业大学, 陕西 西安710072; 2.York University, Toronto M3J 1P3)

摘要：主要考虑绳系卫星释放阶段的姿态运动对空间系绳系统稳定性产生的影响。基于欧拉-牛顿法建立绳系卫星的姿态动力学与运动学方程，研究了释放阶段系绳与卫星之间固定点存在静态不对称性时,卫星姿态的稳定性。为抑制释放阶段卫星姿态运动对系绳系统稳定性产生的不利影响，设计了一种基于Lyapunov函数方法的非线性姿态控制器。数值仿真及分析验证了该控制器可实现卫星姿态的稳定。

关键词：绳系卫星；释放；姿态控制；Lyapunov函数

空间系绳系统是指利用系绳将2个或多个卫星相连所形成的系统[1]，可用于清除空间碎片，产生推力，进行微重力环境下的科学实验等[2-4]。近50年来，空间系绳系统以其独特优势得到广泛关注，许多学者对其动力学与控制问题进行了广泛而深入的研究[1,5]。在空间系绳系统整体的动力学与控制的研究领域，一般将绳系卫星视为质点，忽略其姿态运动[6]。但在实际任务中，卫星的姿态运动可能会对系统稳定性产生影响。例如，OEDIPUS-A实验中，绳系卫星在系绳释放阶段出现了不期望产生的空间姿态运动[7]。再入角是卫星返回地球成功与否的最主要影响因素[8]，系绳释放阶段产生的卫星姿态运动有可能影响其再入角，使绳系卫星不能按预定轨迹再入，造成任务失败。此外，其姿态运动也可能导致系绳缠绕卫星，使卫星之间分离初始阶段的安全条件无法保证。因此，有必要研究系绳释放阶段卫星姿态运动对绳系卫星系统稳定性的影响，以及卫星姿态运动的稳定控制。

许多学者用不同方法对这一问题进行了卓有成效的研究。例如，朱仁璋等[9]建立了考虑卫星尺寸的空间系绳系统复杂动力学模型，研究了状态保持阶段卫星的振荡与姿态运动。王晓宇等[10]建立了计入卫星姿态的系绳系统非线性动力学模型，研究了状态保持阶段系统的动力学行为。Lemke等[11]提出通过移动系绳固定点来实现系绳系统姿态稳定的方法。文浩等[12]考虑带可控臂机械臂的系绳系统面内运动，使用非线性最优控制理论研究了释放阶段卫星姿态的控制问题。黄静等[13]研究了旋转二体绳系卫星姿态跟踪控制问题，提出了一种分布式鲁棒最优控制方法。Zabolotnov等[14]研究了系绳释放阶段的卫星空间姿态运动，分析了影响卫星姿态稳定的主要扰动。本文侧重于研究系绳释放阶段，卫星姿态运动对系统稳定性产生的影响。在卫星释放阶段，由于给定系绳张力控制律的作用，易产生较大的卫星姿态运动，使得系绳完成释放时，卫星的姿态较难控制；即使可以控制，也需消耗较多能量。因此，本文基于以上情况提出了一种实现卫星姿态稳定的控制算法。然后设计了一种简单、高效，基于Lyapunov函数方法的绳系卫星姿态稳定的控制算法，便于在星上实现。最后，数值仿真验证了该控制器的有效性。

1空间系绳系统卫星姿态动力学模型

考虑如图1所示的空间系绳系统模型，其由母

星与子星通过系绳相连组成。本文中建模需使用子星本体坐标系cxyz与系绳坐标系cxtytzt，2种坐标系之间的转换关系在图2中表示。子星本体坐标系cxyz中，c为子星的质心，各轴与中心主惯性轴一致。系绳坐标系cxtytzt中，原点c在子星的质心处，cxt轴与系绳上张力的方向平行，cxtyt平面与系绳释放方向和系绳固定点确定的平面平行，zt轴与其他两轴满足坐标系右手定则。子星相对于系绳方向的空间位置由欧拉角α、ψ和φ确定。其中，α为子星本体坐标系纵轴cx与系绳方向之间的章动角；ψ为子星纵轴cx绕系绳方向旋转的进动角；φ为子星绕纵轴cx的自旋角。

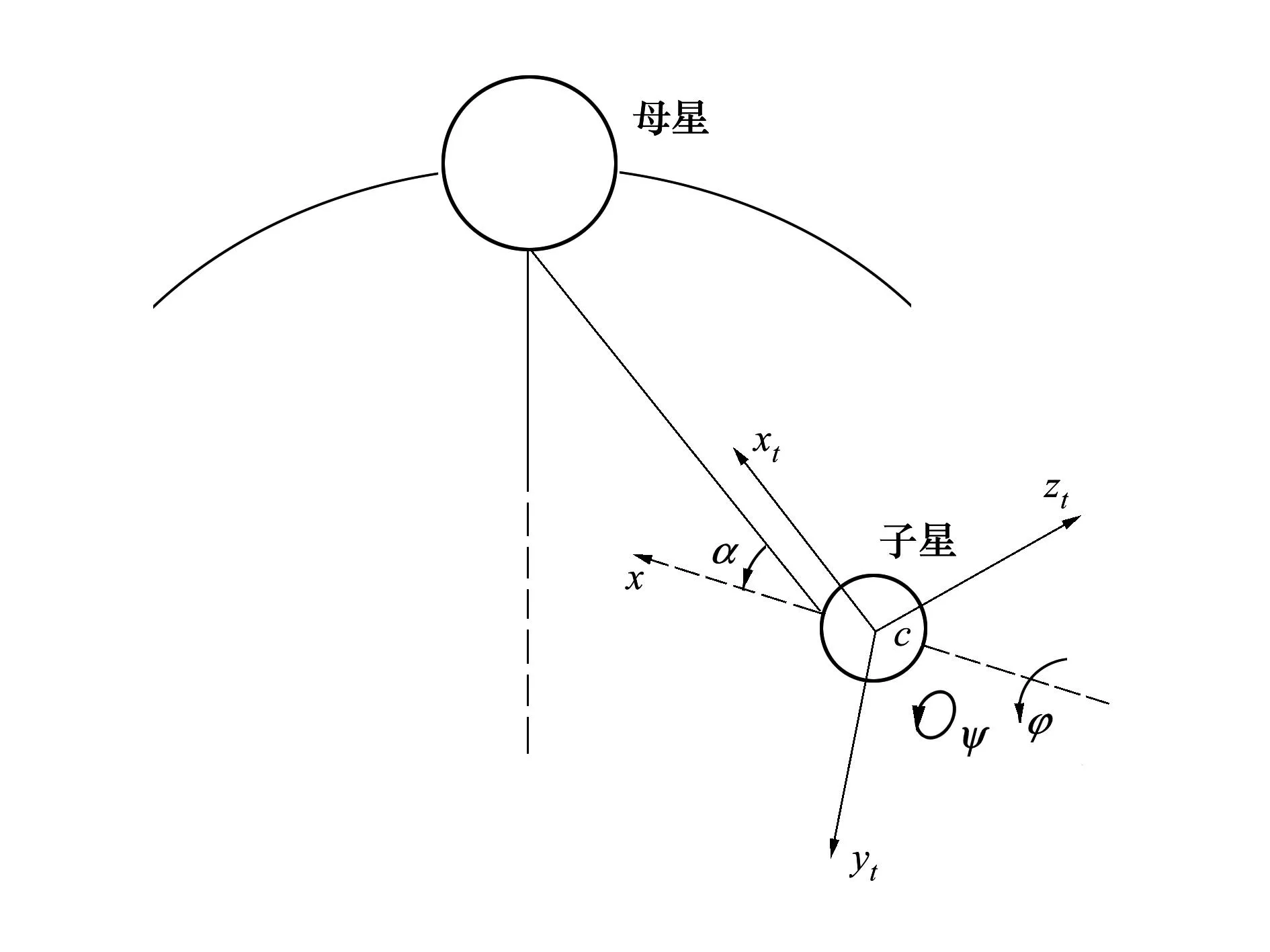
图1　空间系绳系统模型

图2　系绳坐标系与本体坐标系的转换关系

为简化分析过程，考虑如下假设：

1) 母星在圆轨道上运行，其质量远大于子星质量，系绳向下释放；

2) 除系绳上张力产生的张力力矩外，不考虑其他外部干扰力矩；

3) 忽略系绳坐标系cxtytzt的空间运动，假设子星为动力学对称的球形刚体；

4) 由于系绳释放较长，忽略母星对子星空间姿态的影响；

5) 子星的空间姿态可控，且控制器只产生控制力矩，不产生力。

子星的空间姿态运动指的是其绕自身质心的转动，根据前面的假设，子星为刚体，因此其姿态动力学方程可直接根据动量矩定理得到，有如下形式

(1)式中:I为子星的主惯性矩;ω为子星的空间转动角速度;Mt为子星受到的张力力矩。

由于子星本体坐标系cxyz各轴与中心主惯性轴一致,因此可将(1)式在子星本体坐标系cxyz各轴上的投影写出

(2)式中,Ix、Iy和Iz为子星的主惯性矩I在子星本体坐标系cxyz各轴上的投影;ωx、ωy和ωz为子星空间转动角速度ω在子星本体坐标系cxyz各轴上的投影;Mtx、Mty和Mtz为子星受到的张力力矩Mt在子星本体坐标系cxyz各轴上的投影。Mt由下式确定

(3)

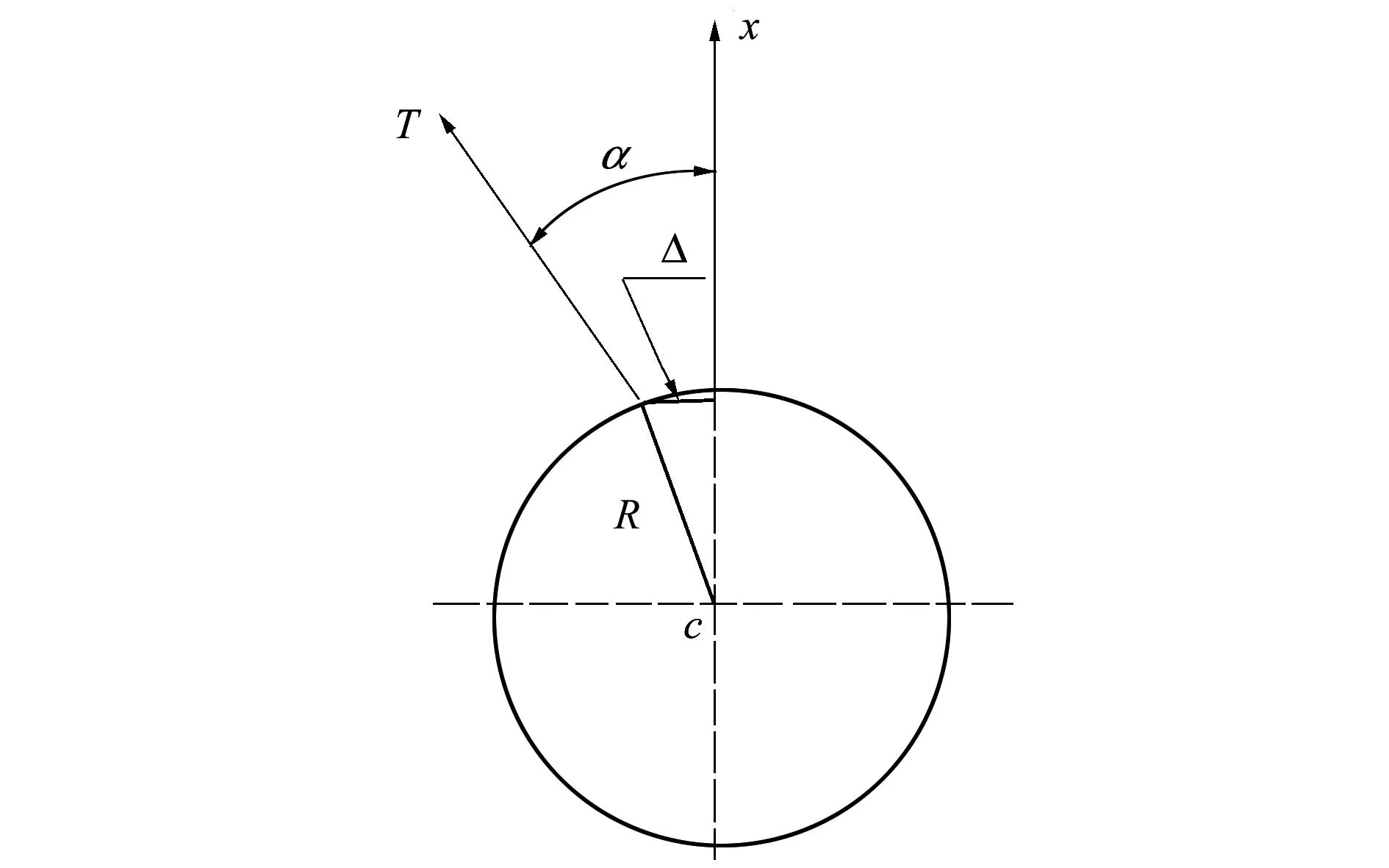
图3　系绳固定点不在子星轴cx时的示意图

为了描述子星姿态的运动学方程,本文采用欧拉——牛顿法建立运动学方程,根据图2在系绳坐标系cxtytzt下写出子星姿态的运动学方程

(4)由于系绳在释放阶段与子星除固定点外没有其他接触,根据子星几何形状,当子星为接近球形或者球形时,章动角α不可能超过90°。因此本文采用欧拉角表示的子星姿态运动学方程不存在章动角奇异的情况。

2空间系绳系统模型及系绳释放阶段控制律

为表示系绳释放阶段空间系绳系统的运动,本文使用文献[15]中的系统模型,其动力学方程如(5)式所示。

3Ω2sinθcosθcos2β

(5)

式中,L为系绳释放长度,θ为系绳相对地垂线的面内偏角,β为面外偏角,Ω为母星沿圆轨道运动的角速度,T为系绳张力。

本文对上述模型采用文献[15]给出的两阶段张力控制律的改进形式控制系绳释放。第1阶段系绳以较低速度释放,最终释放一定长度,实现母星与子星的安全分离。使用的控制律如下

(6)式中:m为子星质量;L0为第1阶段释放的最终长度;a、b和c为控制律的参数。

第2阶段系绳以较大速度先加速后制动释放到预定的长度,最终的释放速度为零。使用如下的改进继电控制律

(7)

式中:Tmin和Tmax为释放阶段设定的最小和最大张力值;t1n和t2n为切换时间;kn和km确定切换的平滑性;t1、t2、T1和Tk为控制参数。两阶段张力控制律在控制系绳按预定要求释放的同时,也在子星上产生张力力矩扰动。因此有必要对子星受到的张力力矩扰动进行抑制。

3子星姿态稳定控制器的设计

系绳释放阶段,子星姿态稳定控制的预期是使子星在受到扰动力矩作用时仍可实现自身姿态的稳定。本文中子星受到的扰动为系绳张力力矩,为体现控制器在其他扰动存在时的效果,设计控制器时不考虑张力力矩扰动。下面给出实现子星姿态稳定的控制器。

定理1如果使用下列控制器

(8)

那么系统(2)和(4)满足Lyapunov稳定性理论,是稳定的。式中,kx、ky和kz是选取的正参数。

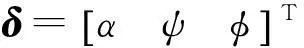
(9)

对(9)式关于时间求导得:

(10)

将(2)式和(4)式代入(10)式整理之后得:

(11)

将(8)式代入(11)式有:

因此,系统是稳定的,定理得证。

本文中,系绳释放阶段需要对子星进行连续的姿态稳定控制。因此,设计出的控制器可以以磁力矩器来实现。

4数值仿真分析

4.1仿真条件

给定释放初始轨道高度为300km,地球引力常数μ=398 600km3/s2,平均半径R0=6 371.02km。母星与子星之间的初始距离为0.1m,初始分离速2.5m/s。系绳第1阶段最终释放长度L0=3km,系绳最终释放30km。最终系绳相对地垂线的面内偏角为-56°,面内角速度为0s-1;面外偏角和角速度都为0。张力控制律中的系数使用下山单纯形法可优化求解得到(见表1)。

子星转动惯量,Iy=Iz=0.32km·m2,子星半径R=0.2m。子星姿态角的初始扰动为α(0)=25°,φ(0)=ψ(0)=0°。子星本体坐标系cxyz三轴上的角速度初始扰动为ωx(0)=0.01s-1,ωy(0)=ωz(0)=0s-1。取控制器中的正参数kx=ky=kz=1。

4.2仿真结果与分析

首先不引入控制器,只考虑系绳释放阶段张力力矩扰动下,子星的空间姿态运动。当Δ=0时,系绳固定点在子星纵轴cx上,子星章动角α的变化趋势如图4所示;当Δ=0.02 m时,系绳固定点不在子星纵轴cx上,子星章动角α的变化趋势如图5所示。

对比图4和图5,系绳释放阶段,子星的姿态角α随着静态误差Δ增大(系绳固定点与纵轴cx直接距离的增大),也相应增大。因此,系绳释放阶段,Δ是不希望存在的。但在卫星实际制造时,系绳固定点不一定在子星纵轴cx上,难免产生误差。因此本文对Δ≠0的情况下,子星的姿态运动进行分析和控制研究。

只考虑Δ=0.02 m空间系绳系统系绳释放阶段系绳张力力矩扰动作用下,子星的姿态运动。仿真结果如图5～图8所示。

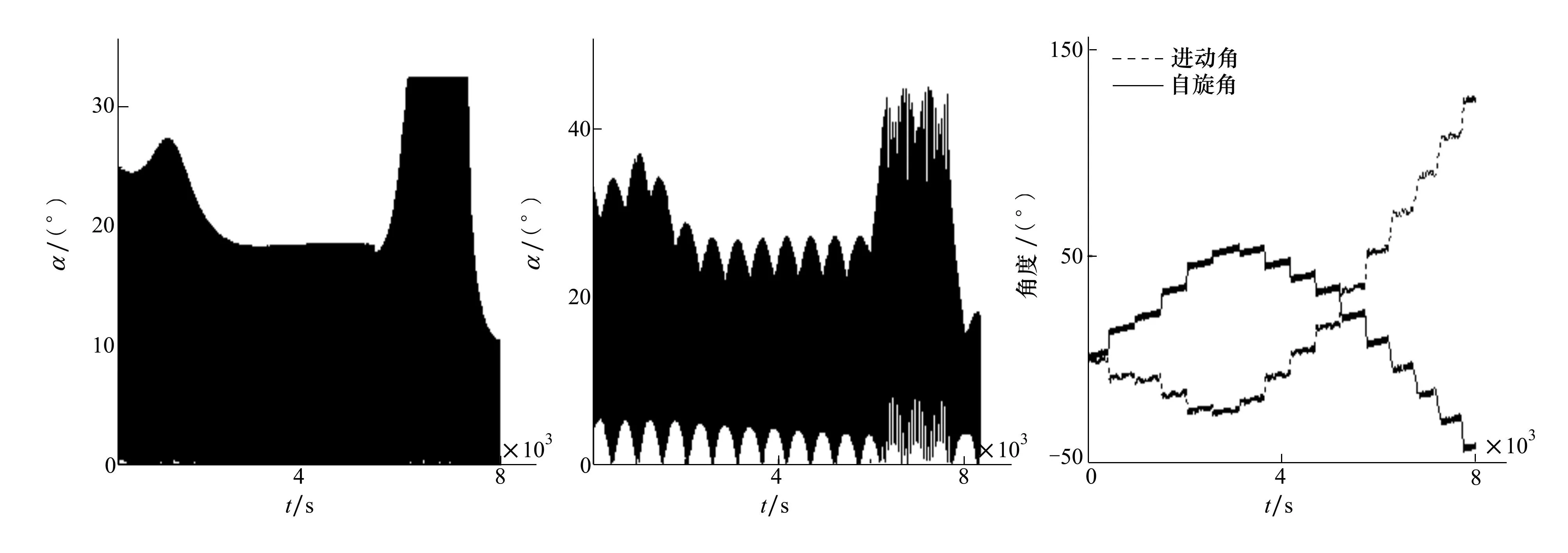
图4　Δ=0 m时章动角的变化曲线　　　图5　Δ=0.2 m时章动角的变化曲线　　　图6　进动角和自旋角的变化曲线

图5和图6给出系绳释放阶段,子星受到张力力矩的扰动后,姿态角的变化曲线。给定章动角α初始扰动为25°时,随着系绳的释放,α在0～50°之间剧烈振荡,且振荡最剧烈发生在系绳快速释放阶段。通过对比图5章动角α的变化和图7中的张力T的变化,可发现章动角和张力之间存在反比例对应关系,张力减小时章动角振荡幅度增加,张力恒定时章动角振荡振幅也恒定,张力急剧减弱时章动角振幅急剧增加。给定进动角ψ和自旋角φ的初始扰动为0°时,ψ先减小到-30°,之后一直增加,系绳释放结束时为140°;φ先增加到60°,之后一直减小,系绳释放结束时为-50°;进动角和自旋角的最小和最大值基本上同时出现。姿态角在系绳释放阶段的剧烈振荡,可能导致系绳缠绕子星,破坏母星与子星分离时的安全条件。此外,系绳释放结束时,较大的姿态角,会使子星姿态运动失稳。因此,有必要对系绳释放阶段的子星姿态运动进行稳定控制。

表1　控制律的参数值

图7　系绳长度与张力变化曲线　　　图8　系绳张力力矩变化曲线　　　图9　加入控制后章动角的变化曲线

图7给出了系绳释放长度与张力变化的趋势,系绳最终释放30km,张力的最大值在2N附近,且系绳释放长度与张力的变化基本成正比关系。图8给出系绳释放阶段,张力力矩随时间变化的曲线。张力力矩与图7中张力成正比。张力增大时,子星本体坐标系cxyz 3个方向上的张力力矩也随之剧烈振荡,总的趋势也为增大;张力基本不变时,张力力矩振荡幅度也很小,基本不变。cx轴向的张力力矩在0附近随着张力变化而振荡变化;cy和cz方向的张力力矩基本关于0对称,随着张力增大振荡变化,最值为0.035N·m附近。

在(2)式中引入基于Lyapunov函数方法设计的姿态控制器,对系绳释放阶段子星姿态进行稳定控制,数值仿真结果如图9～图12所示。

引入控制力矩之后,系绳的释放长度和张力没变化。图9给出了给定章动角初始扰动25°时,随着系绳释放,张力值发生变化,章动角一直下降,最终在15s左右时达到稳定状态;图10给出进动角和自旋角初始扰动0°时,在初始2s一直增加,达到0.001 5°左右,之后一直振荡下降,最终在12s左右稳定。张力力矩在系绳释放阶段虽然对子星姿态一直存在扰动作用,但在加入姿态控制器之后,姿态角在15s左右都很好的收敛到稳定状态附近,消除了系绳的剧烈振荡,避免了系绳缠绕子星,系绳所受应力超过强度极限造成断裂,使系统失效的情况发生。

图11给出了加入控制器后张力力矩的变化曲线。与图8对比,张力力矩在子星本体坐标系cxyz三轴方向剧烈振荡的情况消失,cy和cz方向上张力力矩变化的趋势对称。图12给出控制力矩对时间的响应曲线,控制力矩主要作用在前20s,最大值大约为0.6N·m。因此,系绳释放阶段对子星的空间姿态进行控制,可在初始阶段快速稳定子星姿态,能量消耗很少。系绳释放阶段,子星空间姿态的稳定,为空间系绳系统相关任务的成功进行提供了保证。

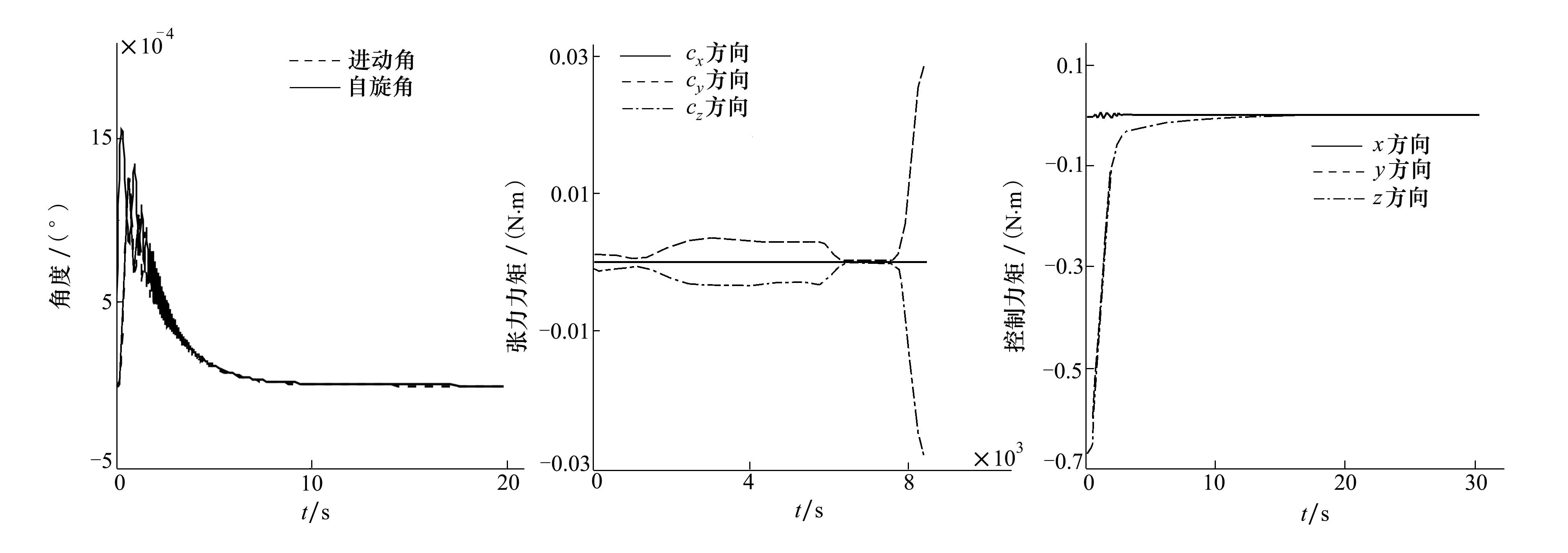
图10　　　　加入控制后进动角和　　　图11　　　　加入控制后张力力矩的图12　控制力矩的变化曲线　　　自旋角的变化曲线　　　变化曲线

5结论

本文考虑了空间系绳系统系绳释放阶段，子星的空间姿态运动对系统稳定性产生的影响。基于欧拉-牛顿法建立了绳系卫星姿态运动学与动力学方程，研究了系绳与卫星之间固定点存在静态不对称性时，卫星姿态运动的稳定性。为消除释放阶段卫星姿态运动对系绳系统稳定性产生的不利影响，设计了一种基于Lyapunov函数方法的非线性姿态控制器。由于对卫星姿态运动学与动力学方程没有进行线性化与解耦，姿态控制器的能量消耗很少，因此实际应用中有很大的使用价值。仿真结果表明，该控制器可很好地抑制外界扰动的影响。

参考文献：

[1]TrogerH,AlpatovAP,BeletskyVV,etal.DynamicsofTetheredSpaceSystems[M].CRCPress, 2010

[2]MisraAK,ModiVJ.ASurveyontheDynamicsandControlofTetheredSatelliteSystems[C]∥TethersinSpace, 1986

[3]JohnsonL.TheTetherSolution[SpacePropulsion,ElectrodynamicTether][J].Spectrum,IEEE, 2000, 37(7): 38-43

[4]ObergJ.SavingMirwithaRopeTrick[J].Spectrum,IEEE, 2000, 37(7): 32-37

[5]CartmellMP,McKenzieDJ.AReviewofSpaceTetherResearch[J].ProgressinAerospaceSciences, 2008, 44(1): 1-21

[6]KumarKD.ReviewonDynamicsandControlofNonelectrodynamicTetheredSatelliteSystems[J].JournalofSpacecraftandRockets, 2006, 43(4): 705-720

[7]TycG,HanRPS.AttitudeDynamicsInvestigationoftheOEDIPUS-ATetheredRocketPayload[J].JournalofSpacecraftandRockets, 1995, 32(1): 133-141

[8]李爱军,韦汉林,王长青. 基于空间系绳系统辅助返回的再入条件计算分析[J]. 西北工业大学学报, 2014, 32(5): 730-736

LiAijun,WeiHanlin,WangChangqing.CalculatingandAnalysisofRe-EntryConditionforSpaceTethered-AssistedReturnSysteminEllipticOrbit[J].JournalofNorthwesternPolytechnicalUniversity, 2014, 32(5): 730-736 (inChinese)

[9]朱仁璋,雷达,林华宝. 绳系卫星系统复杂模型研究[J]. 宇航学报, 1999, 20(3): 7-12

ZhuRenzhang,LeiDa,LinHuabao.ASophisticatedDynamicalModelofTetheredSatelliteSystems[J].JournalofAstronautics, 1999, 20(3): 7-12 (inChinese)

[10] 王晓宇,金栋平. 计入姿态的绳系卫星概周期振动[J]. 振动工程学报, 2010, 23(4): 361-365

WangXiaoyu,JinDongping.Quasi-PeriodicOscillationofaTetheredSubsatellitewithAttitude[J].JournalofVibrationEngineering, 2010, 23(4): 361-365 (inChinese)

[11]LemkeLG,PowellJD,HeX.AttitudeControlofTetheredSpacecraft[C]∥NASA,AIAA,andPSN,InternationalConferenceonTethersinSpace,Arlington,VA. 1986

[12] 文浩,陈辉,金栋平. 带可控臂绳系卫星释放及姿态控制[J]. 力学学报,2012,40(2):408-414

WenHao,ChenHui,JinDongping.DeploymentandAttitudeControlofaTetheredSubsatellitewithControllableArm[J].ChineseJournalofTheoreticalandAppliedMechanics, 2012,40(2):408-414 (inChinese)

[13] 黄静,刘刚,马广富. 含不确定性的绳系卫星姿态的鲁棒最优控制[J]. 宇航学报,2012, 33(10): 1423-1431

HuangJing,LiuGang,MaGuangfu.NonlinearRobustOptimalAttitudeTrackingofTetheredSatelliteSystemwithUncertainties[J].JournalofAstronautics, 2012, 33(10): 1423-1431 (inChinese)

[14]ZabolotnovYM,NaumovON.MotionofaDescentCapsuleRelativetoItsCenterofMassWhenDeployingtheOrbitalTetherSystem[J].CosmicResearch, 2012, 50(2): 177-187

[15] 扎伯罗特诺夫·尤里. 空间系绳系统运动动力学与控制导论[M]. 王长青译,北京:科学出版社,2013

ZablotnovYuriy.IntroductiontoDynamicsandControlinSpaceTetherSystem[M].WangChangqingTranslator.SciencePress,Beijing, 2013 (inChinese)

Nonlinear Stability Control of Tethered Sub-Satellite Attitude in Deployment

Wang Changqing1, Du Chonggang1, Li Aijun1, Z.H.Zhu2

(1．Northwestern Polytechnical University，Xi'an 710072，China 2．York University，Toronto M3J 1P3，Canada)

Abstract:This paper studies the impact of tether deployment on the attitude dynamics of the tethered sub-satellite. The dynamics model of the tethered sub-satellite is derived from the Newton - Euler equation of motion and the stability of tethered sub-satellite′s attitude motion is studied with the consideration of tether attachment offset from the symmetric axis of the satellite. Based on the dynamic analysis, a Lyapunov type nonlinear attitude controller is derived for the attitude motion of the tethered sub-satellite, which is disturbed by the unwanted offset of tether attachment. Simulation results and their analysis demonstrated preliminarily that the newly proposed controller is effective and efficient.

Keywords:tethered sub-satellite, deployment, attitude control, Lyapunov function

中图分类号：V11

文献标志码：A

文章编号:1000-2758(2016)01-0060-07

作者简介：王长青(1973—),西北工业大学副教授、博士，主要从事飞行器控制与仿真、智能控制及空间系绳系统动力学与控制等研究。

基金项目：2011年度国家国际科技合作专项资助

收稿日期：2015-09-02