电涡流耗能动力吸振器设计与试验研究

李斌, 牛文超, 徐兆懿

(西北工业大学 航空学院, 陕西 西安　710072)



电涡流耗能动力吸振器设计与试验研究

李斌, 牛文超, 徐兆懿

(西北工业大学 航空学院, 陕西 西安710072)

摘要：针对飞机垂尾抖振抑制的需要,提出一种空间布局紧凑、基于非接触式电涡流耗能机理、阻尼可设计的动力吸振器设计方案。电涡流耗能机制的引入保证该动力吸振器具有良好的环境适应性、耐久性和可靠性。基于电磁场理论,建立了电涡流阻尼力的计算模型,获得电磁阻尼的设计规律,通过与试验结果对比,验证了电涡流阻尼模型的准确性。并以等效悬臂梁结构为对象,应用最优参数设计原理确定动力吸振器参数,设计制造了动力吸振器样机。试验结果表明,该电涡流动力吸振器具有良好的吸振性能,最大减幅比可达98%。

关键词：动力吸振器;永磁体;电涡流阻尼力;抖振抑制;最优设计参数

当飞机进行高机动性飞行时,垂尾时常处于不稳定涡流中并产生抖振现象,激起结构的弯扭模态振动,使飞机结构出现振动疲劳问题。动力吸振器是结构振动控制最常见的手段之一,它一般分为主动型、被动型、半主动型、混合型4种形式[1]。主动可调型动力吸振器系统复杂,受成本高、可靠性差、适航性等制约,目前很少应用。而被动式动力吸振器作为最常见的形式具有原理和结构简单、可靠性和稳定性高、不需要外界提供能量等特点。传统动力吸振器的阻尼环节一般采用橡胶材料、油阻尼、摩擦阻尼等形式,但由于在实际应用中会出现橡胶材料易氧化,油阻尼器易漏油和摩擦阻尼易磨损等问题,因此采用传统阻尼材料的动力吸振器在应用中受到一定限制。另外这些阻尼环节的阻尼参数常常难以定量设计,难以达到最优阻尼设计的要求。

基于电涡流耗能原理的动力吸振器能够提供一种非接触式阻尼力,大大降低往返式运动部件的磨损,提高了其耐久性和可靠性,并可实现刚度和阻尼的分离设计,因此受到研究者的重视。20世纪80年代,Gunter等[2]为NASA航天飞机主发动机低温涡轮泵的转子系统研制了一种分块盘型永磁被动非旋转型电涡流动力吸振器,应是最早利用电涡流动力吸振器的研究。Kienholtz等[3]提出了一种桶状电涡流动力吸振器,并将其应用到哈勃望远镜的精密光学仪器减振系统中。Karnopp[4]设计了用于车辆悬挂减振的电涡流动力阻尼器。目前,MOOG公司已经研制出用于航天结构振动控制和飞机抖振抑制的电涡流动力吸振器[5],但在国内则还未见类似产品出现。

由于飞机垂尾内部空间有限,吸振装置对耐久性与可靠性要求高,因此本文提出一种空间布局紧凑、基于非接触式电涡流耗能机理、阻尼可设计的动力吸振器设计方案。并通过试验研究,验证电涡流动力吸振器的吸振效果。

1电涡流阻尼

1.1电涡流阻尼的产生机制

根据麦克斯韦理论,当导体处于变化的磁场中或切割磁感线时,金属内部会产生电涡流。电涡流垂直于磁场方向运动会产生洛伦兹力阻碍这种相对运动,这种电磁阻力与导体运动方向相反,与速度大小成正比,与结构振动中的粘性阻尼力特性一致。目前基于电磁阻尼的动力吸振器结构构型有多种形式,主要区别为磁体与导体之间的相对运动方式不

同,其原理均为导体与磁铁发生相对运动来产生电涡流。考虑到垂尾内部空间有限,本文采用图1所示的磁铁在导体管内部作相对运动的布局方案。该方案结构紧凑、占用空间小,通过导体切割磁铁侧围磁场,在导体管内产生诱导电涡流,形成电磁阻力。导体管采用电导率高的T2紫铜管,中心磁铁采用圆柱型稀土强磁体。

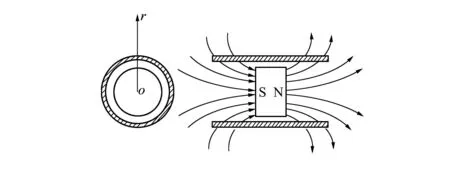
图1　导体相对磁场运动布局方案

1.2圆柱永磁铁的磁场模型

目前主要有2种方法计算磁铁的磁感应强度[6]:①偶极子模型,它适用于计算与磁铁相距较远区域的磁感应强度;②环形电流模型,将永磁铁视为环形电流,它适用于计算磁铁近距区域的磁感应强度。故本文采用环形电流模型。

图2　柱面坐标与积分变量定义

令圆柱永磁铁的半径为R,以圆柱体几何中心为原点,建立柱坐标系(r,θ,z),如图2所示。由于磁场分布具有轴对称性,因此柱坐标(r,z)所表示的环向任意一点的磁感应强度相等。如图2,在圆柱磁体表面上任取一电流微元Idl,它在外围空间柱面任意一点(r,z)处的磁感应强度可应用毕奥-萨法尔定律计算

(1)

式中,μ0为真空导磁率、I为永磁体的表面等效电流、L为圆柱永磁铁高度、dl为微元矢量、R1为等效电流微元到(r,z)点的距离、R1为等效电流微元到(r,z)点的矢量。

在xz平面上任意一点P(r,0,z),则

(2)

式中,A=Rcosθi+Rsinθj,B=ri+zk。

矢量dl表示为

dl=-Rsinθi+Rcosθj

(3)

将(2)式与(3)式代入(1)式,并沿环向积分,可得z高度处等效环向电流对(r,z)点的磁感应强度

(4)

(5)

采用换元法对两式进行积分,将θ替换为π+2φ代(4)式、(5)式中,并沿磁体高度进行积分,可得整个圆柱磁体在(r,z)点产生的磁感应强度为

(6)

(7)

式中,∏(n,k)是第3类椭圆积分变量

(8)

其存在以下性质

K(k)和E(k)分别为第1、第2类椭圆积分变量,定义为

(9)

(10)

式中

(11)

则(6)式、(7)式可化简求得(r,z)点的磁感应强度为

(12)

(13)

式中,Br、Bz分别为圆柱永磁铁外围柱面空间任一点的径向和z轴方向的磁感应强度分量,z′为永磁铁沿z轴方向积分变量。

假设圆柱永磁铁沿轴向均匀充磁极化,则圆柱永磁铁表面的等效电流I可简化为

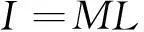
(14)

式中,M为永磁铁的饱和磁化强度。

1.3电涡流阻尼力与等效阻尼系数计算

当圆柱形永磁铁在铜管内以速度v沿z轴方向运动时,忽略边沿效应,铜管壁上诱导产生的电流密度矢量j可写为

(15)

式中，σ为铜管的电导率。由于Bz的矢量方向与v平行,其与v的矢量积为0,因此不产生电流。则铜管受到的电磁阻力可表示为

(16)

舍去Bz的作用,体积分可进一步简化为如下单重积分形式,z向的电涡流阻尼力为

(17)

式中,b为铜管中径,δ为铜管厚度,H为铜管高度。

由(17)式可知,电涡流阻尼力与导体速度成正比,因此电涡流等效阻尼系数c为

(18)

1.4影响电涡流阻尼系数的几何因素

由(18)式可知,电涡流诱导阻尼系数除与导体电导率和厚度有关外,还与磁铁和导体管的尺寸有密切关系。下面通过数值算例分别研究阻尼系数与铜管高度、永磁铁半径、永磁铁高度和永磁铁与导体管间距g的关系。算例的基本输入参数如表1所示,考虑了后续动力吸振器设计所需的基本参数限制要求。

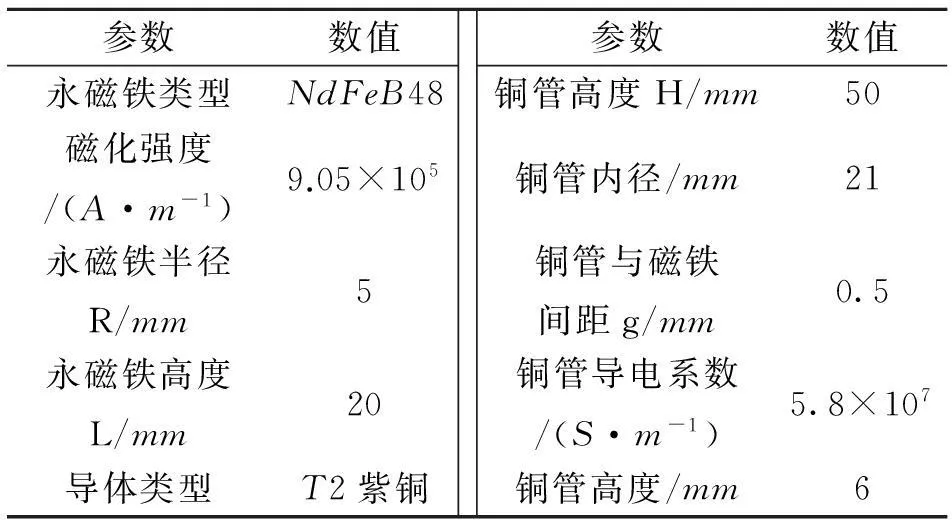
表1　计算参数

以H为自变量,保持其它参数不变,计算等效阻尼系数随H的变化规律,结果如图3所示。可以看出,铜管高度小于30mm时,阻尼系数几乎随铜管高度呈线性变化,但随着铜管高度的增加,曲线斜率逐渐减小,当铜管高度大于40mm时等效阻尼系数趋于稳定。

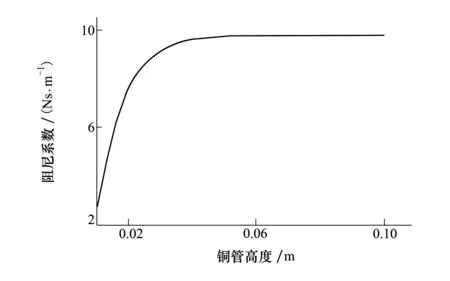
图3　阻尼系数随铜管高度的变化规律

以磁铁半径R为自变量,铜管内径随磁铁半径同步变化,其他参数不变,分析磁铁半径对等效阻尼系数的影响规律,等效阻尼系数几乎随磁铁半径呈线性变化。同理以磁铁高度L为自变量,保证铜管高度远远大于永磁铁高度,避免因铜管高度不足而引起阻尼系数变小,得到阻尼系数随永磁铁高度的变化规律,在一定范围内,等效阻尼系数也几乎随磁铁高度呈线性变化。

此外,永磁铁与铜管间距g也会对阻尼系数产生显著影响。以g为自变量(铜管内外径随g同步变化),得到阻尼系数随间距g的变化规律。可以发现,随着g的增加,阻尼系数迅速减小,几乎为线性变化,因此为充分发挥电涡流耗能效应,g值应越小越好,但加工精度限制了g的取值。在实际应用中考虑到加工精度等因素,一般选为g=0.5 mm。

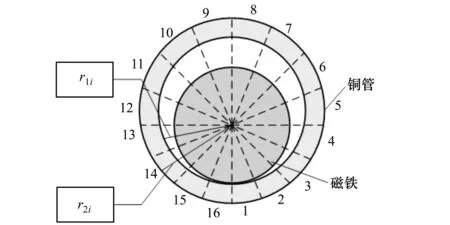
图4　割圆法示意图

由于加工精度等因素,实际应用中不能保证永磁铁一定在铜管中间运动。以一种极限情况为例,当磁铁偏离中心线0.5mm时,即磁铁一端与铜管内壁相接触,分别计算了磁铁半径和高为10mm*10mm与12.5mm*10mm2种情况的等效阻尼系数。由于(18)式无法直接计算偏心情况,所以本文采用一种数值上的简化处理方法但能反映各变量之间关系的阻尼系数解析表达式计算等效阻尼系数

(19)

式中，r1i、r2i分别为磁铁中心到每一弧段中点处铜管的内外壁距离。本文采用割圆法近似计算偏心后的阻尼系数,将铜管等分为16份,如图4所示,分别计算每块产生的阻尼,并进行叠加。得到结果如表2所示:

表2　等效阻尼系数

通过结果发现,偏离后的阻尼系数与未偏离的相对误差均小于1.1%。由此推断,微小的磁铁偏心对等效阻尼系数的影响非常小可忽略其影响。

2电涡流动力吸振器设计

2.1控制对象

参考Joseph等[7]对F/A-18飞机垂尾抖振的分析结果,以垂尾稍部选定的吸振器安装点为参考点,可推导得到对应一阶弯曲振型的垂尾等效单自由度动力学模型。等效模型的模态质量、模态刚度、模态阻尼系数、固有频率分别为

me=29.2 kg,ke=263 740 N/m

现以该模型为对象,进行动力吸振器设计。考虑到垂尾内部空间的限制,不可能安装单一的大动力吸振器,可采用将单个大质量动力吸振器分解为多个小质量动力吸振器的方案进行解决。对于本例,可采用10个小动力吸振器方案。

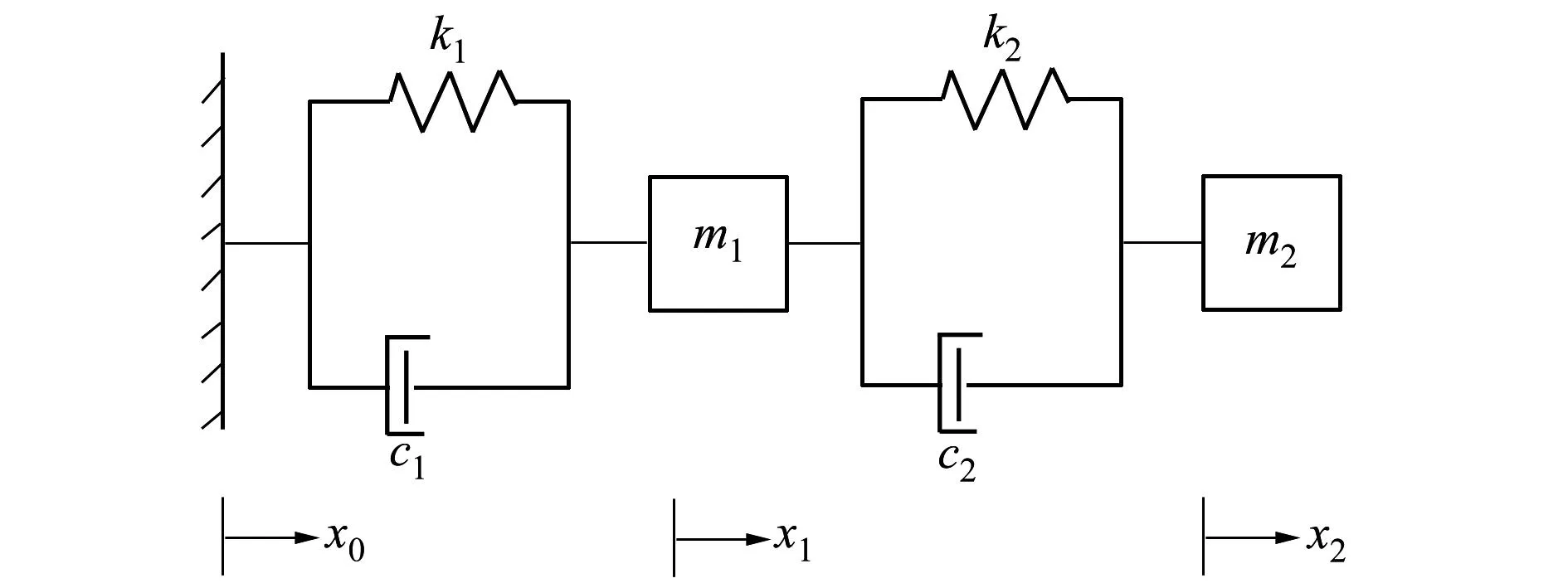
图5　二自由度振动模型

为进一步讨论小质量动力吸振器参数的确定,建立如图5所示的等效二自由度动力学模型,其中m1=me/10,k1=ke/10,c1=ce/10为被控对象的动力学等效相似模型,m2、k2、c2分别为待设计的小型动力吸振器参数。

2.2参数设计

参考背户一登[1]动力吸振器参数调优设计方法,当被控对象的动力学参数与吸振器的质量确定时,k2、c2的最优值可根据(20)式计算

(20)

式中,μ为质量比m2/m1。

上节已给出了被控对象的质量、刚度和阻尼参数,下面进一步确定动力吸振器的质量。动力吸振器的质量元素对被控对象的位移响应幅值影响较大,通过仿真分析可以得出被控系统最大位移响应与动力吸振器质量的关系。可以发现,被控系统的最大位移响应随动力吸振器质量增加而减少,且曲线斜率逐渐降低。当动力吸振器质量大于0.45kg时,曲线斜率变为最小且保持不变。考虑到轻型化的设计要求,选定动力吸振器质量为0.45kg。由(20)式可得电涡流动力吸振器理论质量、刚度和阻尼值分别为

m2=0.45 kg,k2=3 051.5 N/m,c2=14.36 Ns/m

根据前文所述,并考虑小型化的设计要求,我们选取铜管高度为60mm左右(可根据设计要求进行微调),厚度为6mm,永磁铁选用磁能密度高的NdFeB48稀土永磁铁,磁铁高度L=10mm,铜管內径与永磁铁半径差g=0.5mm。由(18)式可反求出上述情况下永磁铁的半径R=12.41mm,因此我们选取标准尺寸外径为25mm柱形永磁铁。

根据以上设计参数,本文设计的电涡流动力吸振器的结构形式如图6所示。2个侧边导轨可确保磁体和质量块仅能沿紫铜管中心作竖直运动。

图6　电涡流动力吸振器样机

3电涡流动力吸振器试验验证

3.1等效阻尼模型验证

构建自由衰减试验系统,分别测量了电涡流动力吸振器在安装磁体和未安装磁体2种工况下的自由衰减振动响应,测试结果如图7所示。

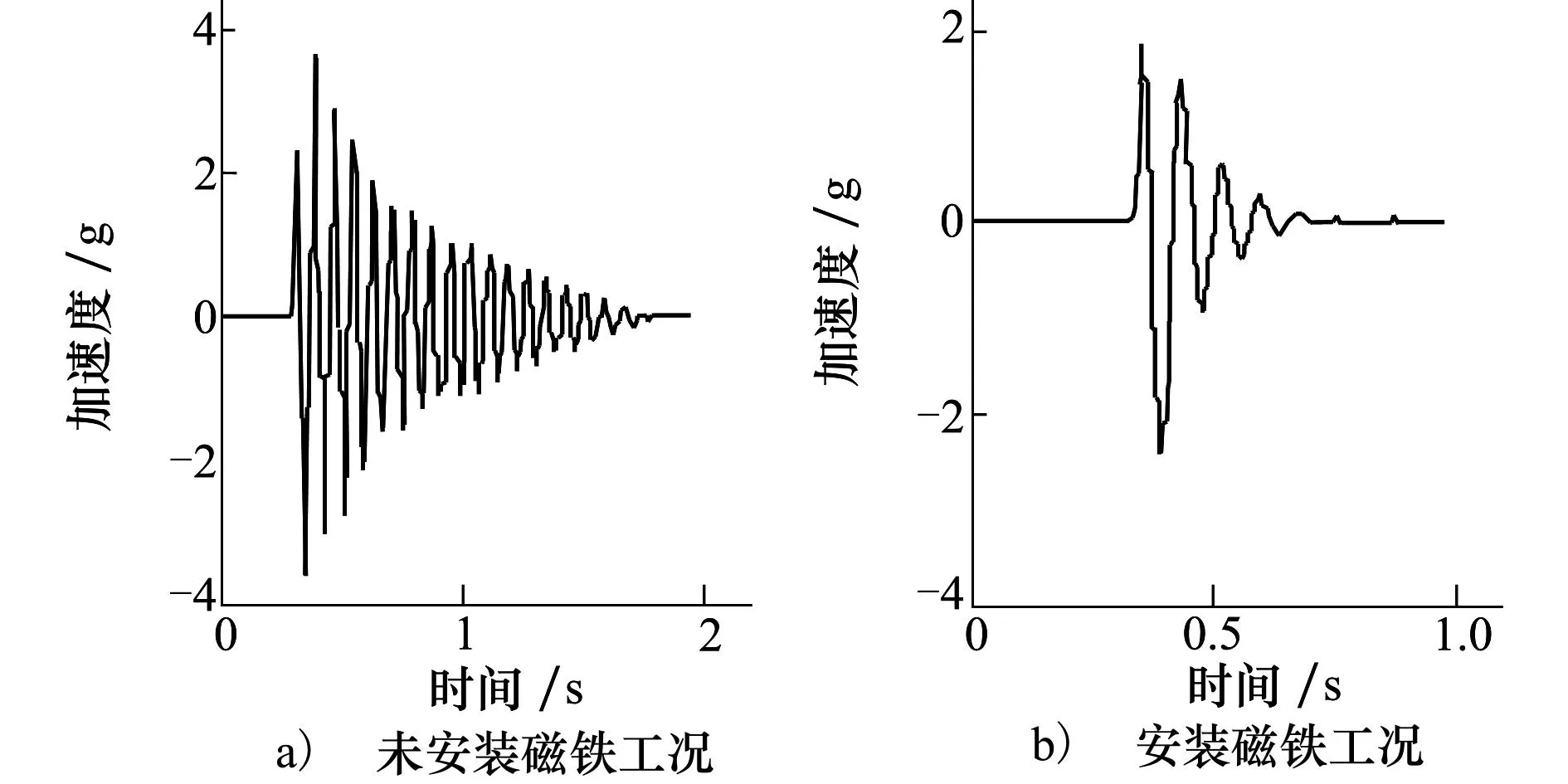
图7　不同工况下电涡流动力吸振器自由振动响应曲线

利用对数减幅率计算2种工况的阻尼值,分别为:13.9N·s/m与1.3N·s/m。可以发现,安装磁铁后动力吸振器阻尼扩大为原来10.7倍,证明电涡流效应产生了可观的阻尼贡献,且该电涡流阻尼调节范围为2～20Ns/m。

根据第1节计算方法,计算得到的本电涡流动力吸振器的理论等效阻尼系数为14.5N·s/m,理论计算结果与试验结果的相对误差为4.3%,验证了本文电涡流等效阻尼计算方法的有效性和准确性。

3.2吸振性能测试

为检验动力吸振器的效果,以图5给出的被控结构基本参数为基准,设计了如图8所示的等效悬臂梁模型,其一弯等效刚度和等效质量与原型基本一致。所设计悬臂梁的悬臂长为555mm、宽为52mm、厚为12mm,端部配重质量为2.279kg。模态试验测得该悬臂梁系统的一阶弯曲固有频率为14.43Hz,与垂尾模型一阶弯曲固有频率的误差为4.56%,由此可见,该悬臂梁系统可以较好地模拟垂尾的一阶振动。

图8　试验装置图

将动力吸振器安装固定在悬臂梁端部,激光位移传感器测量悬臂梁端部位移,加速度传感器安装在吸振器质量块上,如图8所示。通过激振器在悬臂梁的根部输入正弦扫频信号对系统进行强迫振动试验,分别测量该系统在安装与未安装电涡流动力吸振器情况下的位移频响曲线。

图9给出了系统不同工况下5～20Hz频带范围内的频响函数。未安装电涡流动力吸振器梁的最大位移响应为0.937 8mm,安装动力吸振器后梁的最大位移响应变为0.018 1mm,悬臂梁的最大减幅率达到98%。由此可见,在满足最优参数设计条件下,本文所构建的电涡流动力吸振器具有良好的减振效果,符合设计预期。且可通过调节吸振器质量和刚度调节吸振器的工作频段,以适应不同飞机垂尾抖振抑制要求。

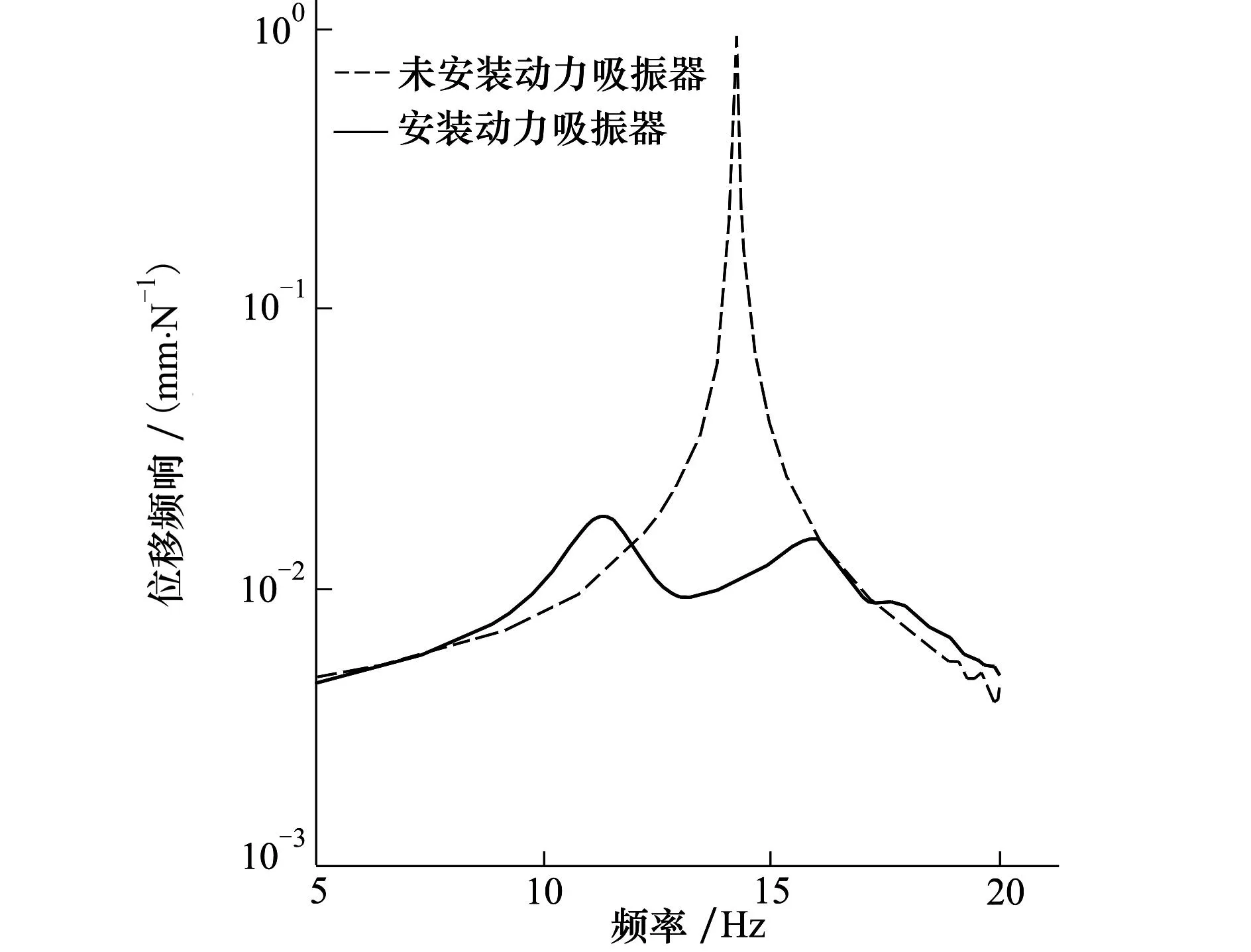
图9　一阶模态的频响曲线

4结论

1) 本文基于电磁场理论,建立了电磁阻尼力计算模型,并开展了变参分析,获得了电磁阻尼的设计规律。通过与试验结果对比,验证了电涡流阻尼解析模型的准确性。

2) 本文以F/A-18飞机垂尾的等效模型为控制对象,基于动力吸振器最优设计理论,确定了电涡流动力吸振器的具体设计参数。设计制作了被控对象和电涡流动力吸振器样机,并开展相应试验。试验结果表明,该电涡流动力吸振器具有良好的吸振性能,最大减幅比可达98%,且该型电涡流动力吸振器的有效频段适用于飞机垂尾抖振抑制的要求。

参考文献：

[1]背户一登. 动力吸振器及其应用[M]. 北京:机械工程出版社,2013:1-21

KazutoSeto.DynamicVibrationAbsorberandItsApplication[M].RenMingzhang,Translator.Beijing,ChinaMachinePress, 2013: 22-50 (inChinese)

[2]GunterEJ,HumphrisRR,SeversonSJ.DesignStudyofMagneticEddy-CurrentVibrationSuppressionDampersforApplicationtoCryogenicTurbomachinery[R].NASA, 1983,CR-173273:1-6

[3]KienholzD,SmithC,HaileW.AMagneticallyDampedVibrationIsolationSystemforaSpaceShuttlePayload[J].InternationalSocietyforOpticsandPhotonics, 1996, 2720: 272-280

[4]KarnoppD.PermanentMagnetLinearMotorsUsedasVariableMechanicalDamperforVehicleSuspensions[J].VehicleSystemDynamic, 1989, 18: 187-200

[5]CSAEngineeringInc.PermanentMagnetandElectromechanicalDevices,Materials,AnalysisandApplications[EB/OL]. (2010)[2015-09-20].http:∥www.csaengineering.com

[6]EbrahimiBabak,KhameseeMirBehrad,GolnaraghiMFarid.DesigningandModelingofaMagneticShockAbsorberBasedonEddyCurrentDampingEffect[J].JournalofSoundandVibration, 2008, 315: 875-889

[7]CSAEngineeringInc.AMagneticTuned-MassDamperforBullet-InducedAirforlVibration[EB/OL]. (2010)[2015-09-20].http:∥www.csaengineering.com

Eddy Current Vibration Absorber Design and Experiments

Li Bin, Niu Wenchao, Xu Zhaoyi

(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:Aiming at the need of vertical tail buffet suppression, a design scheme of dynamic vibration absorber with compact layout and adjustable damping is proposed; this is based on the mechanism of eddy current energy dissipation. Eddy current energy dissipation can ensure that the dynamic vibration absorber has good environmental adaptability, durability and reliability. Based on the electromagnetic theory, the calculation model of eddy current damping force is established and the design rule of eddy damping force is concluded. Through the comparison between the calculations and the experiments, the validation and accuracy of eddy current damping force model are verified. Taking an equivalent cantilever beam system as the object of vibration control, and on the basis of the theory of dynamic vibration absorber optimal design, we determined the optimal parameters of dynamic vibration absorber and completed the design and manufacture of eddy current dynamic vibration absorber prototype. Experimental results show that the maximum amplitude of cantilever beam can be decreased at most by 98%, and the proposed eddy current dynamic vibration absorber has obvious vibration-absorption effect.

Keywords:buffeting, calculations, damping, design, design of experiments, degrees of freedom(mechanics), eddy currents, energy absorption, energy dissipation, experiments, geometry, mathematical models, modal analysis, optimization, permanent magnets, reliability, saturation magnetization, schematic diagrams, vectors, vibration analysis; buffet suppression, dynamic vibration absorbers, eddy current damping, optimal design parameters

中图分类号：V219

文献标志码：A

文章编号:1000-2758(2016)01-0018-07

作者简介：李斌(1975—)，西北工业大学教授、博士，主要从事结构动力学与控制研究。

基金项目：国家自然科学基金(1172238)与中央高校基本科研业务费专项资金(3102014KYJD015)资助

收稿日期：2015-09-24