高超声速热气动弹性中结构热边界影响研究

叶坤, 叶正寅, 屈展

(西北工业大学 航空学院, 陕西 西安　710072)



高超声速热气动弹性中结构热边界影响研究

叶坤, 叶正寅, 屈展

(西北工业大学 航空学院, 陕西 西安710072)

摘要：基于分层求解思路研究结构热边界对高超声速飞行器全动舵面和翼面结构热气动弹性特性的影响。首先,基于CFD求解N-S方程得到热环境,在此基础上进行结构的瞬态热传导分析,进而分析结构由于温度梯度产生的热应力和温度对材料属性的影响下的模态固有特性,然后将结构振型插值到气动网格上,最后,通过求解Euler方程得到流动参数,基于CFD的当地流活塞理论计算气动力,在状态空间中进行了气动弹性分析。通过对4组结构模型进行热气动弹性分析,研究了结构热边界对舵面和翼面热气动弹性的影响,结果表明:对全动舵面而言,结构热边界首先会影响舵轴处结构的热传导过程及温度分布,进而对结构固有频率、频率间距、颤振速度以及颤振频率的变化产生的影响达到了16%。对翼面而言,结构热边界对结构固有频率、频率间距、颤振速度以及颤振频率的变化产生的影响约为1%。因此,工程实际当中,进行热气动弹性分析时应采用合理的结构热边界。

关键词：高超声速;热气动弹性;结构热边界;气动加热;当地流活塞理论

吸气式高超声速飞行器高速飞行时,气动加热效应明显, 飞行器将承受巨大的定常与非定常气动力载荷和气动加热引起的热载荷,此时,结构的弹性力、惯性力、气动力和热应力之间的相互作用将引发热气动弹性问题,气动热效应引起飞行器结构刚度特性的变化将有可能导致颤振速度下降。因此,近年来,围绕高超声速飞行器热气动弹性的研究成为一个热点[1-5]。

国内外许多学者对热气动弹性开展了大量深入的研究。McNamara等[6]通过采用三阶活塞理论计算气动力,采用Eckert参考焓法计算热流,建立了双向耦合的热气动弹性方法,并分别对高超声速飞行器舵面和壁板进行了热气动弹性研究。Lamorte等[7]研究了真实气体效应,湍流转棙位置对热气动弹性的影响,发现转棙位和热应力以非线性因素形式对舵面的热气动弹性特性产生明显影响。Crowel和Falkiewicz等[8-9]研究了高超声速热气动弹性中的降阶模型,基于POD方法建立计算瞬态热传导的降阶模型。Lamorte等[10]研究了转棙位置和热流的不确定性对高超声速二维壁板热气动弹性的影响。杨超等[11]基于双向耦合对二维高超声速曲面壁板进行颤振分析,结果表明:相对于气动热-气动弹性单向耦合壁板颤振结果,双向耦合的结果更危险。吴志刚等[12]分析比较了高超声速全动舵面和小展弦比根部固支翼面的热颤振特性,表明热效应会影响结构动力特性和颤振特性。杨享文等[13]研究了舵面间隙对热气动弹的影响,发现间隙对热气动弹性的影响最大达到6%。史晓鸣等[14-15]考虑攻角对结构热颤振的影响,对大攻角翼面进行了超声速热颤振分析。张伟伟等[16]采用不同的温度分布和结构支持方式,基于CFD的当地流活塞理论,在时域内对高超声速小展弦比大后掠翼进行了热气动弹性仿真。陈文俊等[17]根据国内外大量热气动弹性分析和实验结果,总结和分析了热对气动弹性的影响。李增文等[18]对比了相同结构、不同温度场和不同材料的翼面结构热颤振特性,研究了热应力对结构颤振特性的影响。

目前,绝大部分热气动弹性研究文献中关于结构热传导的处理方法是仅对气动弹性分析的结构进行热传导分析,忽略与之连接的结构对热传导及气

动弹性分析的影响。然而,工程实际当中,一架完整的飞行器是由多个部件结构装配连接而成,对于导弹上的全动舵面/翼面而言,舵面通过舵轴与弹身结构连接,当舵面受到气动加热的影响时,不仅舵面结构内部进行热传导,与此同时,舵面中的热将通过舵轴向与其连接的弹身结构传导,显然翼面结构的热传导也与之类似,并且,发现当热边界采用常规的处理方法时,某些结构模型的分析结果中甚至会出现热边界处局部的热应力超过材料应力极限的情况。因此,全动舵面/翼面结构的热边界条件必然对其热传导过程和附加热应力产生影响,进而影响结构的固有频率以及颤振特性。但是，目前,在舵面/翼面的热气动弹性研究方面,尚未见到细致研究结构热边界对热气动弹性特性影响的文献。因此,无论从学术研究的角度,还是对工程实际而言,细致地研究结构热边界对全动舵面/翼面热气动弹性特性的影响都是一个非常有意义的问题。

高超声速飞行器全动舵面通过舵轴进行偏转以起到配平力矩的作用,刚度比较小,且舵轴附近温度高,气动加热效应比较明显,因此,全动舵面是气动弹性分析中比较薄弱的一个部件。翼面结构作为飞行器最常见的气动部件,其热气动弹性特性同样受到重视,与舵面结构不同,翼面结构根部与机身或弹身连接,而舵面结构只是通过舵轴的根部与机身或弹身连接。因此,本文选取全动舵面和翼面2种典型的结构作为热气动弹性研究的对象,基于分层求解原理分别对4组不同的结构模型进行热气动弹性分析,细致地研究了结构热边界对全动舵面/翼面热气动弹性特性的影响。

1分析思路

本文基于分层求解的思路对舵面/翼面进行热气动弹性分析,将气动力-气动热-结构动力学三者的耦合分解为定常气动热-结构动力学和非定常气动力-结构动力学两部分分别求解,忽略结构变形和振动对热环境的影响,假设环境温度保持不变。热气动弹性的研究思路如图1所示,①基于CFD技术求解RANS方程得到物面附近的热环境;②进行热传导分析;③进行热应力分析;④进行模态分析;⑤基于RBF方法将结构振型插值到气动网格上;⑥求解Euler方程得到流动参数,采用基于CFD的当地流活塞理论,在状态空间中对结构进行了气动弹性分析。

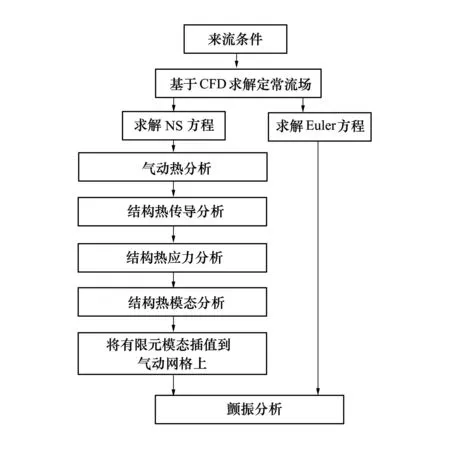
图1　分析流程图

2计算方法

2.1流体控制方程

控制方程采用积分形式的N-S方程和Euler方程,求解N-S方程得到气动热,求解Euler方程得到壁面当地流动参数,其统一形式如下:

(1)

式中:Q=[ρ,ρu,ρv,ρw,e]T,ρ、u、v、w、e分别为空气密度、x、y、z方向的速度分量和单位体积的总内能,n为积分边界的单位法向向量,V为流场积分域,∂V为积分域的边界,F为通量项,它包括无黏项FE和黏性项Fv两部分:

F=FE+Fv

空间离散采用AUSM+格式,采用SST湍流模型,且湍流模型采用中心格式,时间推进采用LU-SGS格式,采用绝热壁面边界条件。令Fv=0,则方程变为Euler方程。

2.2气动热计算

假设结构为非黑体,则流体与结构之间的热量传递过程中热流平衡关系为

(2)

式中，Qaero为流体对结构表面的输入热流,即对流传热,Qcond为结构向内部的热传导,Qrad为结构表面向空间辐射散热的热流,Qstrd为结构由于温度增加而储存的热流。

流体对结构表面的输入热流Qaero采用牛顿冷却公式计算

(3)

式中，Tw为壁面温度,在结构热传导分析中每个时间步更新一次,初始温度为298 K;Tc为壁面流体温度,在此取流场靠近壁面第1层网格单元格心的温度,通过求解N-S方程得到;h为壁面对流换热系数,由公式(4)计算得到

(4)

(5)

式中，cl为气体比热;u*为速度因子,Cμ=0.09为湍流模型常数;k为湍动能。T+为无量纲温度,由BAKader壁面函数热律[19]计算得到

(6)

式中

(7)

式中,Pr为气体普朗特数,λl为气体热传导系数,Δn为靠近壁面第1层和第2层网格格心距离;μ为黏性系数,由求解N-S方程得到。

热辐射采用Stefan-Boltzmann定律修正公式进行计算

(8)

工中,ε为物体辐射发射率,本文取0.8,σ为斯坦福常数为5.669 7×10-8(w/m2K4),T∞取为298K。

2.3结构热传导

结构热传导计算采用Fourier定律,基于Fourier定律的三维瞬态热传导控制微分方程在无内部热源时形式如下

(9)

式中,T为结构温度,t为热传导时间,λs、cs、ρs分别为结构热传导系数、比热和密度。方程离散采用显式差分格式,时间离散采用一阶向前差分,空间离散采用二阶中心差分。

由此可求得结构温度场,并作为温度载荷加载到结构上进行结构热应力分析,并得到结构的热应力分布。

2.4结构模态分析

考虑温度效应并忽略阻尼的结构自由振动方程如下所示

(10)

式中，M为质量阵,Ks(T)为传统的结构刚度矩阵,考虑到结构材料属性随温度变化,故而为温度T的函数;Kσ(T)为热应力引起的附加几何刚度矩阵。

当结构发生简谐振动,即u=Usin(ωt)时,方程变为

(11)

通过求解上述特征方程可以得到结构的前i阶固有圆频率ωi和振型φi。

2.5非定常气动力计算

非定常气动力计算采用文献[20]中基于CFD技术的当地流活塞理论,其基于模态坐标的气动力为

(12)

式中

(13)

(14)

(15)

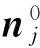
对于一个特定计算状态,用Euler方程得到定常流场后,即可确定A和B,进而得到了气动力关于广义位移的表达式。

2.6颤振分析

应用拉格朗日方程,基于模态坐标的的运动方程可以写为

(16)

式中，M为质量矩阵,G为结构阻尼矩阵,K为刚度矩阵,Q为广义气动力。实验测定G很困难,这里令G为零。把(12)式代入(16)式得

(17)

(18)

式中

(19)

给定M∞、V∞、β∞,则C为一实矩阵,这样气动弹性系统的稳定性分析就转化为求解状态方程中矩阵C的特征值问题了。当某一特征值的根轨迹穿越虚轴时,系统的稳定性将发生变化,该根的虚部表示颤振的频率。详细推导过程参见文献[20]。

3验证算例

本文验证算例采用文献[21]中的翼面模型,该翼面厚度均为0.008m,β∞=1kg/m3,M∞=7.0,α=0°,翼根全部固支。本文计算了结构温度T=323K时的固有频率和颤振特性,并与文献结果进行了对比,如表1所示,其中F1、F2分别表示结构前两阶固有频率,Vflutter为颤振速度。由此可见,本文计算结果与文献的结果吻合的较好,说明本文的分析方法是可信的。

表1　热气动弹性计算结果对比

4计算模型

4.1气动模型

本文气动模型为三维导弹下的2个模型, 图2b)为全动舵面气动模型,图2c)为翼面模型气动模型。为简化模型,舵面模型中的舵面和翼面模型的翼面采用相同的气动外形,舵面结构中舵面通过舵轴与弹身连接,翼面模型当中翼面根部直接与弹身连接。如图2a)所示,为降低计算量,数值模拟时只取半模,采用非结构混合网格进行空间离散,为尽量准确地计算舵面和舵轴间隙及其附近的热环境,在这些区域进行了网格加密,空间网格单元总数约500万。飞行参数为:β∞=0.336 2kg/m3,M∞=5.0,T∞=298K,α=3.5°热传导分析中,热传导总时间为300s,初始时刻结构温度Tinitial=298K。

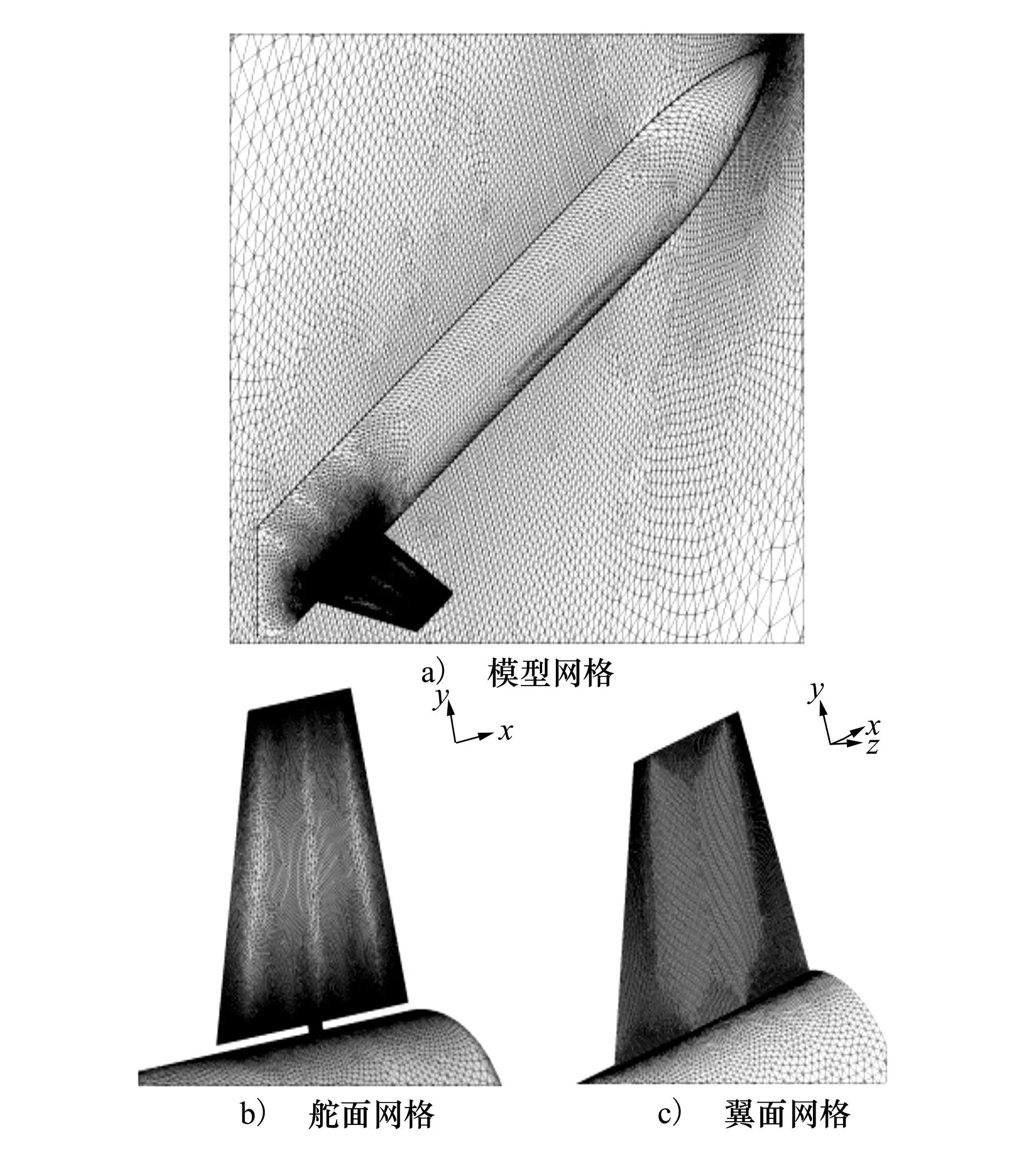
图2　舵面和翼面模型及网格

4.2结构模型

为研究结构热边界对全动舵面和翼面热气动弹性特性的影响,设计4组结构模型进行热传导分析,分别对应舵面和翼面的2种不同热边界条件。如图3a)所示,仅对舵面和舵轴结构进行热传导分析,舵轴根部平面处于环境中,无热流的输入和输出,记为Case1。如图3b)所示,热传导分析时同时考虑舵面结构和弹身结构,舵面中的热可通过舵轴传导至弹身结构,记为Case2。如图3c)所示,仅对翼面结构进行热传导分析,翼面根部平面处于环境中,无热流的输入和输出,记为Case3。如图3d)所示,热传导分析时,同时考虑翼面结构和弹身结构,翼面中的热可通过根部平面传导至弹身结构,记为Case4。

图3　结构模型

所有结构模型均简化为实心结构,对结构进行热应力以及模态分析时,全动舵面结构的约束条件为舵轴根部平面固支,舵面材料采用TIMETAL834,舵轴和弹身的材料采用1Cr18Ni9Ti。翼面结构的约束条件为翼面根部平面固支,翼面材料采用TIMETAL834,弹身的材料均采用1Cr18Ni9Ti,TIMETAL834和1Cr18Ni9Ti随温度变化的材料属参见文献[13]。

5计算结果与分析

通过上述分层求解方法,研究了随结构热传导的进行,结构热边界对全动舵面和翼面结构热气动弹性特性随时间变化的影响。

5.1结构热边界对全动舵面热气动弹性的影响

为细致地分析结构热传导过程,如图4所示,在舵面结构上选取7个观测点,其中点1～点3分别位于舵面中心区域、舵面根部翼型前缘点和后缘点,点4～点7位于舵轴外表面及其内部。

图4　舵面结构温度观测点

图5为热传导分析中Case1和Case2舵面上观测点温度随时间变化的对比,2种热边界条件下,点1和点2温度在较短时间内达到最大并迅速趋于稳定,点3的温度在100s左右达到最大。对于同一观测点,2种热边界条件下,点1～点3的变化规律基本相同,且热传导稳定后的温度也非常接近。点4～点7的变化规律略有区别,Case1中150s左右温度达到最大并稳定,而Case2中的温度达到稳定的时间略长于Case1,并且稳定后的温度两者最大相差约500K。这正是由于Case1中只对舵面进行热传导分析,舵面结构中的热无法传导至其他结构,而Case2中,舵面结构中的热可通过舵轴根部传入与之连接的弹身结构,这不仅降低了舵轴结构处热传导稳定后的温度,并且增加了热传导过程达到稳定所需的时间。

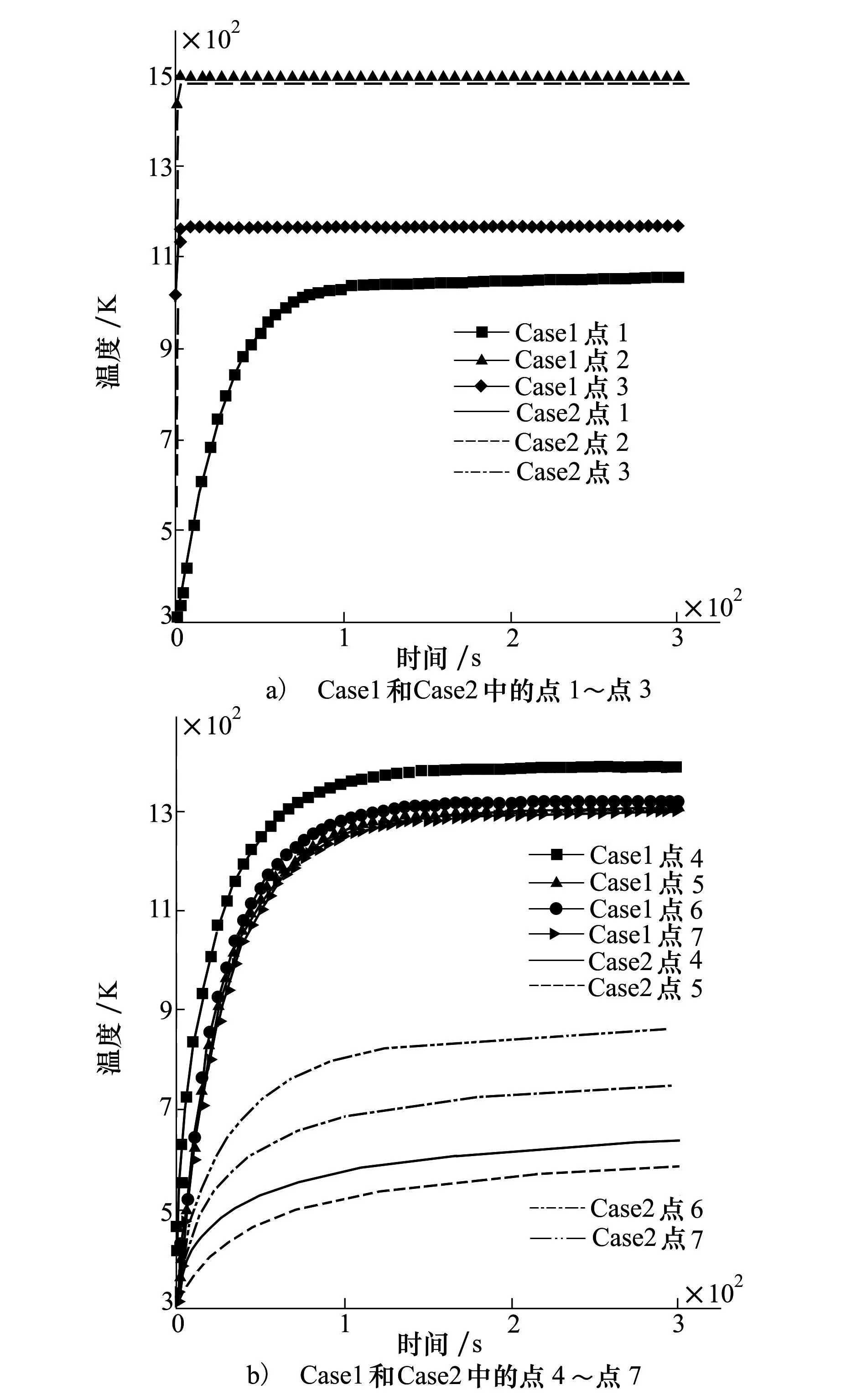
图5　观测点温度随随时间的变化

上述热传导分析结果表明:热边界条件对舵面上的温度基本没有影响,但是对舵轴结构处的热传导过程和稳定后的温度产生明显的影响。

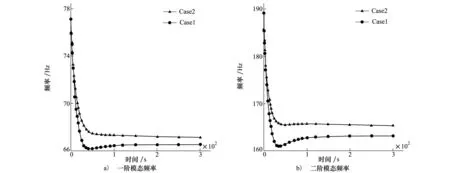
图6　频率随时间变化对比

图6为2种热边界条件下结构固有频率随时间变化的对比,可以看出,Case1和Case2中结构的固有频率随时间变化的趋势基本相同,两者都在0～30s时间段内快速下降,30～300s时间段内,频率略有上升并缓慢地趋于稳定,两者都最终在300s时基本达到稳定,并且,Case2中的结构一阶、二阶频率均大于Case1中对应频率,2种结构热边界下,频率达到稳定后,一阶频率下降的幅值最大相差13%,二阶频率下降的幅值最大相差24%。

根据前面的热传导分析,舵面的温度基本相同,而舵轴中的温度差别明显,Case2中舵轴处结构温度上升的幅度小,降低了结构由于高温引起材料性能下降的影响,使得其舵轴处的刚度高于Case1,进而使得结构的固有频率均高于Case1。

图7～图9分别为2种热边界条件下,舵面一阶频率与二阶频率的间距、颤振速度、颤振频率随时间变化的曲线,三者的变化趋势比较一致,都是先迅速下降,然后略有上升并缓慢趋于稳定,结构热边界对三者下降幅度的影响约为16%。

图7　频率间距随时间变化　　　　图8　颤振速度随时间变化对比图9　颤振频率随时间变化

上述计算结果以及分析过程表明:对于本文全动舵面结构而言,结构热边界对其热传导过程,固有频率、频率间距、颤振频率和颤振速度的变化均产生了比较明显的影响。

5.2结构热边界对翼面热气动弹性的影响

图10为翼面上的温度观测点。图11为热传导分析中Case3和Case4上观测点温度随时间的变化,对于点1而言,2种热边界条件下温度的变化基本相同,都在50s左右达到稳定,且稳定的温度相同,对于点2～点5而言,Case3中观测点的温度快速达到稳定,而Case4中观测点的温度缓慢上升,并最终趋于稳定,且两者稳定后的温度相差约300K。这表明热边界条件对翼面中心区域的温度基本没有影响,但是对翼面根部处的热传导稳定后的温度及热传导过程达到稳定所需的时间均产生明显的影响。

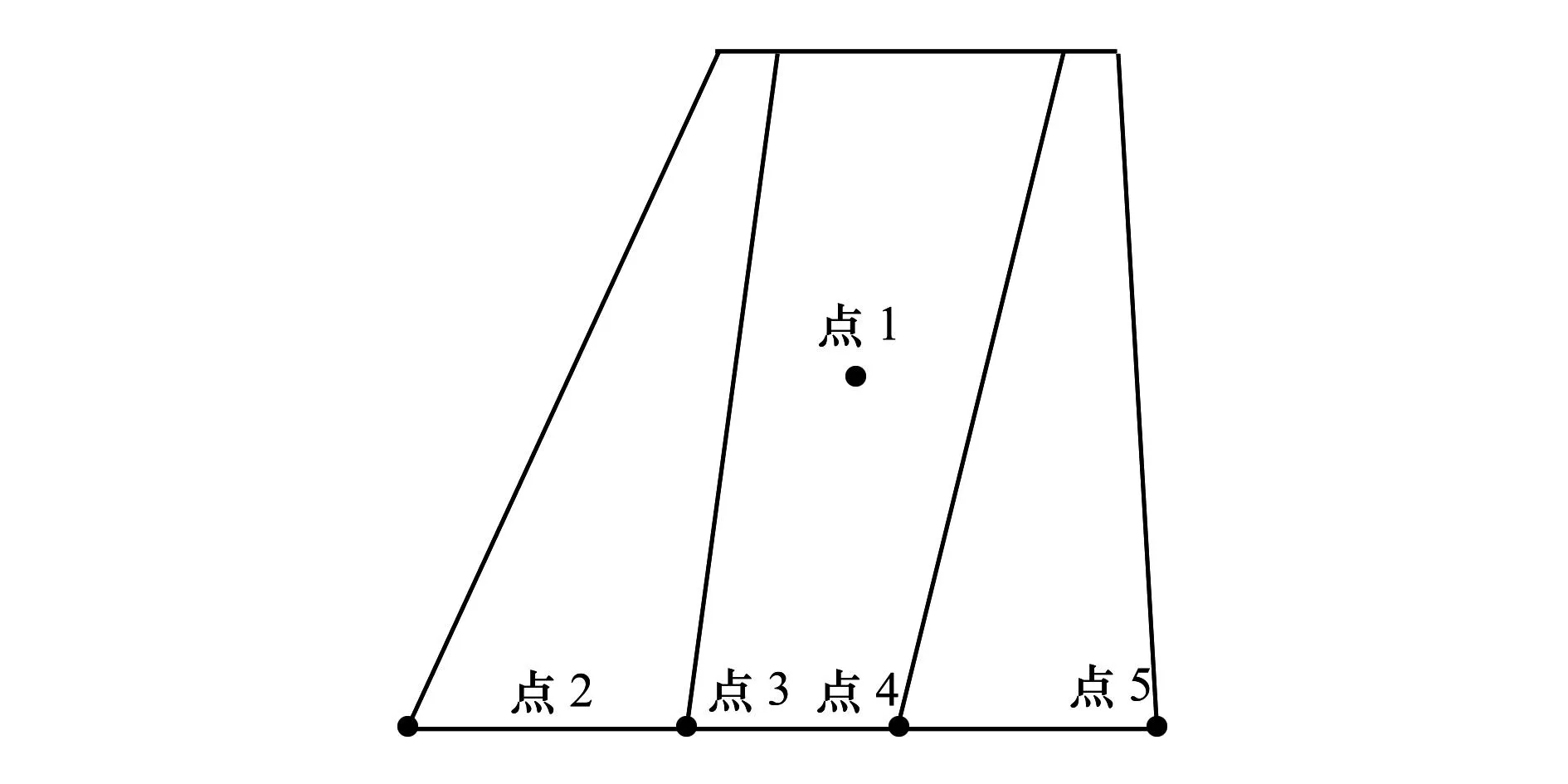
图10　翼面结构温度观测点

图11　观测点温度随随时间的变化

图12为Case3与Case4中结构固有频率随时间变化的对比,可以看出,对于同一频率而言,2种热边界条件下固有频率随时间变化的规律基本相

同。不同之处在于,一阶频率在0～30s时间段内,快速下降并达到稳定,而二阶频率在0～5s时间段内,快速下降,5～80s时间段内,有明显的上升并较快地达到稳定。

2种结构热边界下,热传导分析中翼面中心区域的温度基本相同,翼面根部的温度差别明显,但是,热边界条件对固有频率的影响却很小,并且热效应对翼面的一阶弯曲频率和一阶扭转频率随时间的变化过程产生不同的影响。

图12　频率随时间变化对比

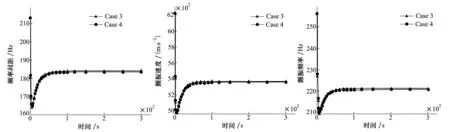
图13　频率间距随时间变化　　　　　图14　颤振速度随时间变化对比图15　颤振频率随时间变化

图13～图15分别为2种热边界条件下,翼面一阶频率与二阶频率的间距、颤振速度、颤振频率随时间变化的曲线,三者的变化趋势基本相同,都是先迅速下降,然后有明显的上升并较快地趋于稳定,热边界对三者下降幅度的影响约为1.2%。

上述计算结果以及分析过程表明:对于本文翼面结构而言,虽然,结构热边界对其热传导过程影响明显,但是,其对固有频率、频率间距、颤振频率以及颤振速度变化的影响较小。

6结论

基于分层求解原理较细致地研究了结构热边界条件对高超声速全动舵面和翼面的热气动弹性特性的影响,得出以下结论:

对于本文的全动舵面结构而言,结论如下:

1) 热传导过程当中,结构热边界条件对舵面中心点的温度变化基本没有影响,但是,对舵轴上的温度产生明显的影响,考虑弹身的连接后,舵轴处温度降低了约500K,且热传导达到稳定所需的时间更长。

2) 2种热边界条件下,舵面结构固有频率、频率间距、颤振频率和颤振速度均随热传导的进行先迅速下降,然后略有上升并缓慢趋于平稳,结构热边界条件对固有频率和颤振特性随时间的变化产生的影响达到16%。

对于本文的翼面结构而言,结论如下:

1) 热传导过程中,结构热边界条件对翼面中心点的温度变化基本没有影响,但是,对翼面根部处温度产生明显的影响,考虑弹身的连接后,翼根处温度降低了约300K,且热传导达到稳定所需的时间更长。

2) 2种热边界条件下,翼面结构固有频率、频率间距、颤振频率和颤振速度均随热传导的进行先迅速下降,然后有明显的上升并较快地趋于稳定,结构热边界条件对固有频率和颤振特性随时间的变化的影响约为1%。

因此,工程实际当中,进行热气动弹性分析时,应考虑结构热边界条件的影响。

参考文献：

[1]KlockRJ,CesnikCES.AerothermoelasticSimulationofAir-BreathingHypersonicVehicles[R].AIAA-2014-0149

[2]杨超, 许赟, 谢长川. 高超声速气动弹性力学综述[J]. 航空学报,2010, 31(1):1-11

YangChao,XuYun,XieChangchuan.ReviewofStudiesonAeroelasticityofHypersonicVehicles[J].ActaAeronauticaetAstronauticaSinica, 2010, 31(1): 1-11 (inChinese)

[3]McNamaraJJ,andFriedmannPP,AeroelasticandAerothermoelasticAnalysisinHypersonicFlow:Past,Present,andFuture[J].AIAAJournal, 2011, 49(6): 1089-1122

[4]LamorteN,FriedmannPP.AerothermoelasticandAeroelasticStudiesofHypersonicVehiclesUsingCFD[R].AIAA-2013-1591

[5]McNamaraJJ,FriedmannPP.Three-DimensionalAeroelasticandAerothermoelasticBehaviorinHypersonicflow[R].AIAA-2005-2175

[6]CullerAJ,McNamaraJJ.StudiesonFluid-Thermal-StructuralCouplingforAerothermoelasticityinHypersonicFlow[J].AIAAJournal, 2010, 48(8): 1721-1738

[7]LamorteN,FriedmannPP.AerothermoelasticandAeroelasticStudiesofHypersonicVehiclesusingCFD[R].AIAA-2013-1591

[8]CrowelAR,McNamaraJJ,ModelReductionofComputationalAerothermodynamicsforHypersonicAerothermoelasticity[J].AIAAJournal,2012,50(1): 74-84

[9]FalkiewiczN,CesnikCES,CrowellAR,McNamara,JJ.Reduced-OrderAerothermoelasticFrameworkforHypersonicVehicleControlSimulation[J].AIAAJournal,2011,49(8): 1625-1646

[10]LamorteN,FriedmannPP,GlazB,CullerAJ,CrowellAR,McNamaraJJ.UncertaintyPropagationinHypersonicAerothermoelasticAnalysis[J].JournalofAircraft, 2014, 51(1): 192-203

[11] 杨超, 李国曙, 万志强. 气动热-气动弹性双向耦合的高超声速壁板颤振分析方法[J]. 中国科学: 技术科学, 2012, 42(4):369-377

YangChao,LiGuoshu,WangZhiqiang.Aerothermal-AeroelasticTwo-WayCouplingMethodforHypersonicCurvedPanelFlutter[J].ScientiaSinicaTechnologica, 2012,42(4): 369-377 (inChinese)

[12] 吴志刚,惠俊鹏,杨超. 高超声速下翼面的热颤振工程分析[J]. 北京航空航天大学学报, 2005, 3(3): 270-273

WuZhigang,HuiJunpeng,YangChao.HypersonicAerothermoelasticAnalysisofWings[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2005, 3(3): 270-273 (inChinese)

[13] 杨享文, 武洁, 叶坤, 叶正寅. 高超声速全动舵面的热气动弹性研究[J]. 力学学报, 2014,46(4): 626-630

YangXiangwen,WuJie,YeKun,YeZhengyin.StudyonAerothermoelasticityofaHypersonicAll-MovableControlSurface[J].ChineseJournalofTheoreticalandAppliedMechanics, 2014, 46(4): 626-630 (inChinese)

[14] 史晓鸣, 杨炳渊. 气动加热环境下大攻角翼面超音速颤振分析[J]. 强度与环境, 2008,35(6):6-13

ShiXiaoming,YangBingyuan.AnalysisofSupersonicFlutteroftheWingWithHighAngleofAttackWithAero-DynamicsHeating[J].Structure&EnvironmentEngineering, 2008, 35(6): 6-13 (inChinese)

[15] 杨炳渊,宋伟力. 应用当地流活塞理论的大攻角升力 面颤振气动力表达式[J]. 上海力学, 1999, 20(3): 223-228

YangBingyuan,SongWeili.ExpressionsaboutAerodynamicForcesofFlutterforWingwithHighAngleofAttackbyLocalFlowPistonTheory[J].ShanghaiJournalofMechanics, 1999, 20(3): 223-228 (inChinese)

[16] 张伟伟,夏巍,叶正寅. 一种高超音速热气动弹性数值研究方法[J]. 工程力学, 2006,23(2):41-46

ZhangWeiwei,XiaWei,YeZhengyin.ANumericalMethodforHypersonicAerothermoelasticity[J].EngineeringMechanice, 2006, 23(2): 41-46 (inChinese)

[17] 陈文俊. 几种气动热弹性设计方法[J]. 战术导弹技术, 2001(5):31-39

ChenWenjun.TheDesigningMethodsforAerothermoelascity[J].TacticalMissileTechnology, 2001(5): 31-39 (inChinese)

[18] 李增文,林立军,关世义. 超声速全动舵面热颤振特性分析[J]. 战术导弹技术, 2008(5): 36-39

LiZengwei,LinLijun,GuanShiyi.ResearchontheThermalFlutterCharacteristicsofHypersonicAll-MovedWing[J].TacticalMissileTechnology, 2008(5): 36-39 (inChinese)

[19]KaderBA.TemperatureandConcentrationProfilesinFullyTurbulentBoundaryLayers[J].InternationalJournalofHeatandMassTransfer, 1981, 24(9): 1541-1544

[20]ZhangWeiwei,YeZhengyin,ZhangChengan,etal.AnalysisofSupersonicAeroelasticProblemBasedonLocalPistonTheoryMethod[J].AIAAJournal, 2009, 47(10): 2321-2328

[21] 张伟伟,夏巍,叶正寅.一种高超音速热气动弹性数值研究方法[J]. 工程力学, 2006,23(2):41-46

ZhangWeiwei,XiaWei,YeZhengyin.ANumericalMethodforHypersonicAerothermoelasticity[J].EngineeringMechanice, 2006, 23(2): 41-46 (inChinese)

Effect of Structural Thermal Boundary on Areothermoelasticity for Hypersonic Vehicles

Ye Kun, Ye Zhengyin, Qu Zhan

(College of Aeronautics, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:The effect of structural thermal boundary on aerothermoelasticity of hypersonic all-movable control surface/wing is studied on the basis of hierarchical solution process. On the basis of CFD technology, Navier-Stokes equation is solved to get the thermal environment. And then transient thermal conduction of structure is analyzed. Then structural modal is analyzed under the effect of structure's thermal stress caused by temperature gradient and material property decrease caused by high temperature, then structural mode is interpolated to the aerodynamic grid; Finally, Euler equation is solved to get flow parameter, and based on CFD local piston theory, aerothermoelasticity is analyzed in state space. Through analyzing aerothermoelasticity of four different structural models, the effect of the structural thermal boundary on aerothermoelasticity of all-movable control surface/wing is analyzed. The results show that: for the control surface in this paper, the structural thermal boundary would firstly affect the heat transfer process and temperature distribution of shaft structure. The effect on the variation of the natural frequency, frequency spacing, flutter velocity and flutter frequency is about 16%. For the wing in this paper, The effect on the variation of the natural frequency, frequency spacing, flutter velocity and flutter frequency is about 1%. Therefore, in practical engineering, reasonable thermal boundary should be used while analyzing aerothermoelasticity.

Keywords:aerodynamic, configurations, aerodynamic heating, aeroelasticity, angle of attack, boundary conditions, calculations, computational fluid dynamics, control surfaces, Euler equations, flow fields, flow velocity, flowcharting, flutter(aerodynamics), heat transfer, hypersonic vehicles, materials properties, mathematical models, matrix algebra, mesh generation, modal analysis, Navier Stokes equatons, Prandtl number, radial basis function networks, structural dynamics, temperature distribution, turbulence models, vectors, velocity, wings; aerothermoelasticity, flutter frequency, flutter velocity, local flow piston theory, structural thermal boundary

中图分类号：V211. 47

文献标志码：A

文章编号:1000-2758(2016)01-0001-10

作者简介：叶坤(1987—)，西北工业大学博士研究生，主要从事高超声速热气动弹性研究。

基金项目：国家自然科学基金(91216202)资助

收稿日期：2015-09-29