纤维丝束带成型工艺参数对弹性性能影响的有限元分析

张宏基, 唐虹, 史耀耀

(1.西北工业大学 机电学院, 陕西 西安　710072; 2.榆林学院 能源工程学院, 陕西 榆林　719000)



纤维丝束带成型工艺参数对弹性性能影响的有限元分析

张宏基1,2, 唐虹1, 史耀耀1

(1.西北工业大学 机电学院, 陕西 西安710072; 2.榆林学院 能源工程学院, 陕西 榆林719000)

摘要：根据复合材料纤维丝束带材料的细观结构，通过推导工艺张力和温度参数作用下纤维丝束带弹性变形理论。利用有限元分析软件建立参数化的细观有限元模型，通过施加合理的载荷及边界条件，对张力及温度作用下纤维丝束带弹性性能参数的变化进行研究。在讨论张力与纤维体积含量关系的基础上，详细分析了张力、温度及纤维体积含量对纤维丝束带弹性性能参数的影响规律。结果表明：随着张力在0～50 N范围内的增大，纤维丝束带弹性模量和剪切模量均呈现先近似线性增大而后保持平稳最后下降的规律。其中，剪切模量下降的趋势更为缓慢；随着温度的升高纤维丝束带的纵向弹性模量表现出先逐渐减小而后趋于稳定的变化规律并且纤维体积含量越高，这种变化趋势越缓慢；横向弹性模量则表现出现先增加后降低的变化规律。而随着温度的升高横向纵向剪切模量均逐渐降低。

关键词：复合材料；弹性性能；纤维丝束带；工艺参数

复合材料纤维丝束带成型是指利用纤维丝、纤维束、纤维带 (统称为：纤维丝束带)等作为预浸料，通过缠绕、铺带、铺丝等工艺将纤维丝束带在一定张力、温度、压力和线速度的作用下，按照预先设定的路径均匀地缠绕或铺放到模具或层板的表面[1]。成型过程中由于张力、温度等参数的作用会引起纤维丝束带性能的变化，而纤维丝束带性能的变化直接导致复合材料制品性能的不稳定或不可预测。其中，弹性常数(弹性模量、剪切模量、泊松比)是最基本的。但对由纤维丝束带成型的复合材料而言，由于丝束带自身的结构、成型工艺以及成型时的温度、张力等工艺参数的影响，导致最终制品具有复杂的细观结构。目前的研究大致可以分为2类：①不考虑成型工艺参数的影响直接对宏观材料的性能进行预测研究；②考虑了工艺参数的影响，研究工艺参数与宏观材料性能之间的影响机理问题。如A. P. Mouritz和 S. Feih[2]建立了一个热-力耦合模型，通过有限元仿真与实验相结合的方法，研究了温度和力对复合材料力学性能的影响。Nguyen等人[3]研究了在紫外线高温加热同时施加拉力的情况下，钢/碳纤维复合材料力学性能的变化，研究指出：单纯紫外线辐射不影响复合材料的拉伸强度，但当以一定的温度照射数小时后环氧树脂粘合剂的拉伸强度降低13.9%，而弹性模量则增加了38%。Mahmood等[4]通过建立材料微观特征体积单元预测三维编织成型复合材料弹性模量，研究指出：纤维体积含量不仅对复合材料应力-应变有十分显著的影响，而且对材料的弹性性能、抗拉强度等都有一定的影响。Xiao等[5]等对碳纤维在温度和时间作用下的机械性能进行了研究，结果表明：碳纤维的杨氏模量随着温度和时间的增加而增大；抗拉强度随着温度的升高显著减小，但延长某一恒定温度的作用时间，碳纤维抗拉强度略有降低或几乎保持不变。卢子兴等[6]在三维全五向编织复合材料细观结构模型的基础上建立其参数化有限元模型深入研究了纤维体积分数、编织角等工艺参数对材料弹性性能和热物

理性能的影响规律。

综上所述，目前的研究都未考虑在成型工艺参数作用下纤维丝束带自身性能的改变对材料的影响。本文以复合材料C纤维丝束带成型过程中工艺张力、温度对纤维丝束带弹性性能的影响为研究对象，采用理论分析和有限元仿真模拟的方法，在对纤维丝束带弹性理论分析的基础上，建立有限元模型分别研究在张力及温度的作用下纤维丝束带的弹性模量、剪切模量等弹性性能参数随张力及温度的变化规律，为复合材料纤维丝束带成型时工艺参数选择、控制、优化及最终制品性能预测、损伤失效的分析提供良好的理论基础。

1纤维丝束带弹性理论分析

1.1张力作用下纤维丝束带弹性变形分析

由于纤维丝束带是由宏观均匀的C纤维原丝和树脂基体在一定条件下合成的，其组分材料均为横观各向同性线弹性体。假设纤维丝束带在受力过程中纤维和树脂基体之间不发生相对滑移和分离。设纤维丝束带的长度和宽度分别为L和W，模型如图1所示，当张力沿纤维丝束带轴向作用时，纤维丝束带将发生弹性变形。

根据复合材料力学理论可知[7-8]，对于纤维丝束带复合材料，其本构方程为：

(1)

式中:σ、ε、ν、γ、E、G分别表示应力、应变、泊松比、剪切应力、弹性模量、剪切模量,同时满足下列关系式。

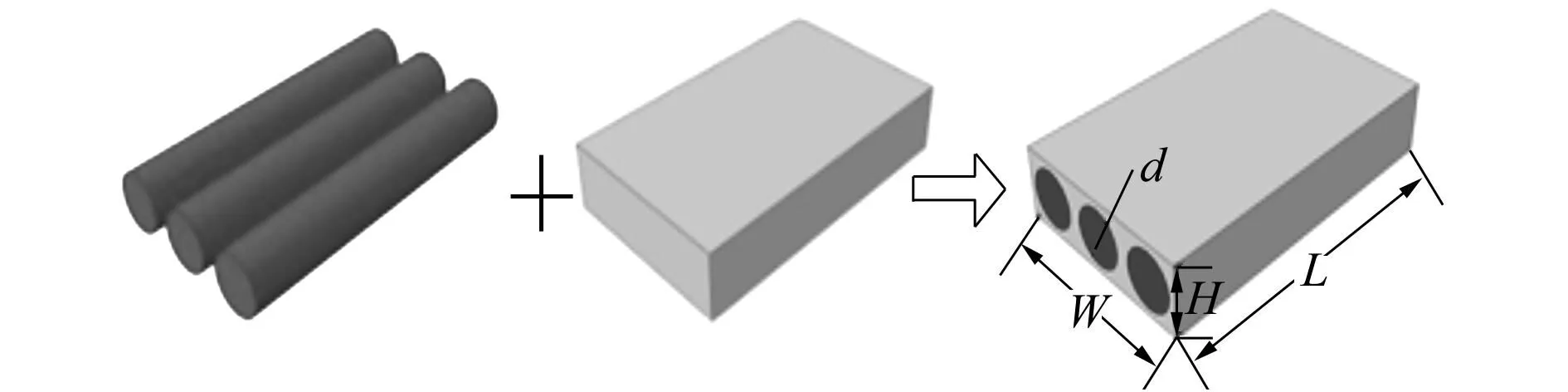
图1　复合材料碳纤维丝束带结构

(2)

分析(1)式可知,对于复合材料纤维丝束带的特征体积单元(RVE)如果已知对应各单向应力状态下的各应变量,便可以求出各弹性常数。例如,在单向应力σx作用下,能求出对于各应变量εx、εy、εz(此时γij为零),得Ex=σx/εx,νxy=-εy/εx,νxz=-εz/εx。以此类推即可求出全部弹性常数。

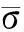
(3)

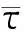
根据单向复合材料理论可知,纤维丝束带显示出各向异性的宏观性能并且纵、横向弹性特性相同,即满足:

(4)

设直角坐标系X、Y、Z与材料坐标系方向一致。此时,按下述方法加载4次,求出各相应应变,对应的等效弹性性能参数由(1)式、(2)式、(4)式计算得到:

1) 加载单向应力σx,则有

(5)

2) 加载单向应力σy,则有

(6)

3) 单独加载应力τxy,则有

(7)

4) 单独加载应力τxz,则有

(8)

同时,应有下列关系式成立

(9)

(9)式也可作为弹性性能参数计算精确性的验证公式。

1.2温度作用下纤维丝束带弹性变形分析

温度作用下纤维丝束带的应变可用6个独立分量εi(i=1,2,…,6)来表征,经绝热可逆过程到终态(T+ΔT,εi+Δεi),根据热力学原理有[9]:

(10)

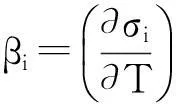
通常情况下应变可表示为正应变δijε0和剪应变τij之和:

(11)

式中

θ为整体应变i,j∈{1,2,3}根据(10)式和(11)式可以得出纤维丝束带温度与应变之间的关系:

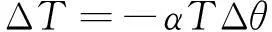
(12)

式中,α=(β11+β22+β33)/3cε,cε=Cε/V0,负号表示纤维丝束带受拉力，压缩时为正。

2有限元模型

2.1基本假设及纤维体积含量的确定

考虑纤维丝束带在张力、温度作用下变形的实际结构,在有限元模型的建立过程中,做出如下假设:(1)纤维丝束带纵、横截面均为四边形,纤维原丝的横截面为圆形,截面参数如图1所示;(2)彼此相邻的纤维原丝之间保持紧密接触,纤维和树脂基体之间保持理想粘结,不产生相对滑移;(3)忽略纤维和树脂基体之间的接触热阻效应。基于上述假设根据图1所示纤维丝束带的细观几何模型,通过给定外形几何参数,可得如下纤维体积含量关系式。

(13)

式中,k为纤维丝束带中所含纤维原丝的数量,利用ABAQUS可建立纤维丝束带特征模型,如图2所示(其中Vf=50%)。

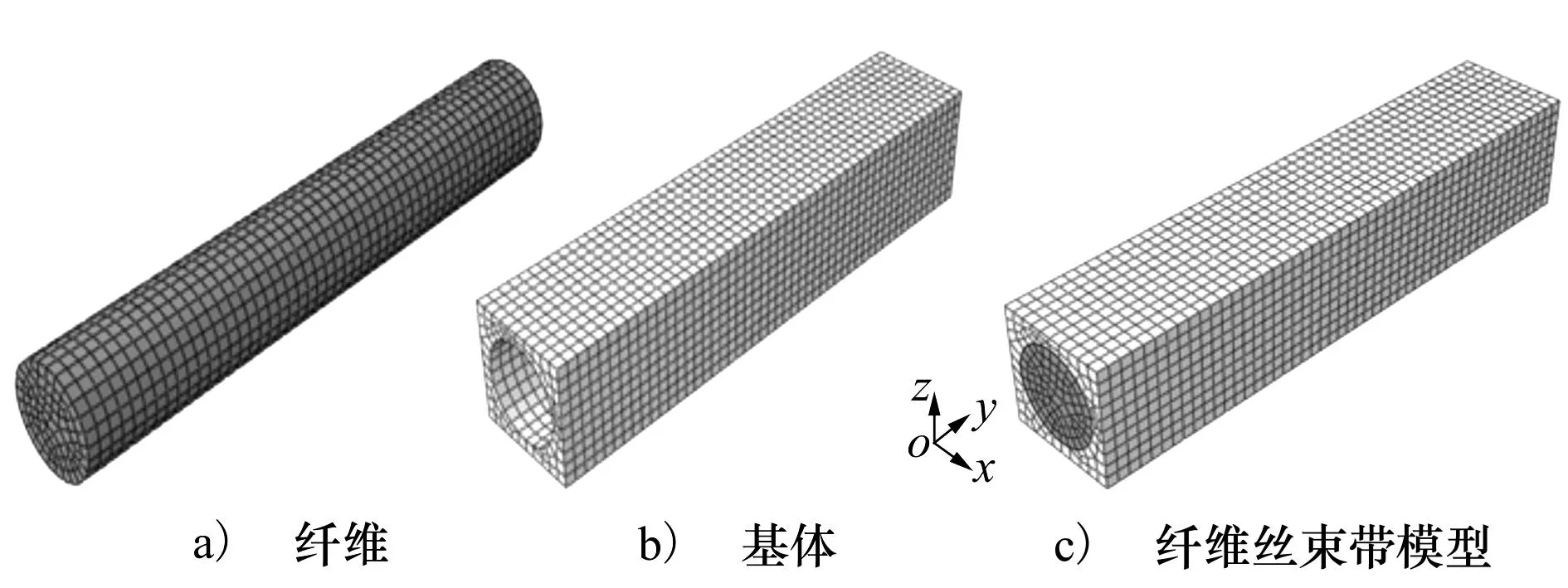
图2　有限元模型网格划分

2.2材料属性及网格划分

复合材料纤维丝束带可看成是有许多纤维原丝与树脂基体复合而成的单向纤维复合材料,其细观结构如图2所示。

本文中使用的碳纤维原丝和树脂基体的弹性性能参数如表1所示。

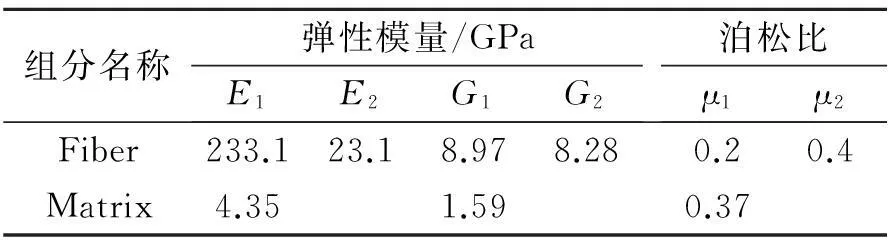
表1　碳纤维和树脂基体弹性性能参数[10]

由于纤维和树脂基体具有不同的材料属性,为了保证划分网格的精度,应分别进行划分。首先对模型的3组表面进行面网格划分,即对每一组表面先划分出一个表面上的网格,之后把网格映射到与其相对的表面上。这样能保证相对平面上的面网格、节点一一对应。然后对基体和纤维分别采用六面体进行扫掠网格划分。最后,将6个面上的面网格删除即可得到模型的实体网格。

2.3周期性边界条件

对于含有周期性单元结构的连续纤维丝束带材料,除施加均匀载荷边界条件外还必须使相邻纤维束之间的公共边界的变形协调,即满足周期性边界条件的变形连续和应力连续条件。

含周期性结构单元的纤维丝束带,其边界上的位移场可表示为[11]:

(14)

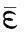
(15)

式中,符号i+和i-分别表示第i组平行面。由(15)式可得

(16)

3工艺参数对弹性性能影响的结果分析

张力及温度是复合材料纤维丝束带成型时最重要的2个工艺参数,直接控制和影响着纤维丝束带的改性过程从而影响着材料的整体结构性能。通过纤维丝束带细观有限元建模分析,给出了工艺张力及工艺温度对复合材料纤维丝束带弹性性能的影响规律。分析过程中保持丝束带原有性能参数和几何参数不变,通过改变张力和温度的大小,分析纤维丝束带弹性参数的变化情况。

3.1张力对纤维丝束带弹性性能的影响

施加张力的目的是控制纤维中树脂含量、增加层间的粘结压力,并使纤维排列得更好。施加的张力太小,纤维取向不好,内部孔隙、间隙含量高,导致产品性能降低;张力过大,纤维磨损严重,还可能使纤维拉断,也会降低产品性能,最佳张力状态是纤维呈直线排列、无松弛现象时给纤维丝束带施加最小张力[12]。在ABAQUS软件中,通过改变纤维原丝含量系数k调节纤维体积含量。可得如图3所示为张

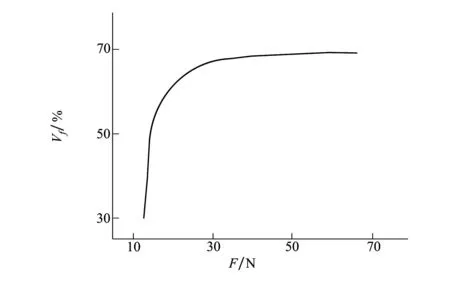
图3　纤维体积含量随张力的变化关系

力F与纤维体积含量Vf的关系图,由图3可以看出,随着张力增加,纤维丝束带纤维体积含量增加。这是由于张力增大纤维丝之间的间隙、基体孔隙减小,从而使得纤维体积含量增加。

由于成型过程中张力的作用会引起纤维丝束带在x、y、z 3个方向上的应力变形,图4为张力F及体积分数对弹性模量Ey的影响规律。

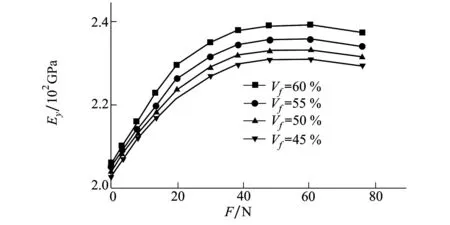
图4　纤维丝束带弹性模量Ey随张力的变化关系

由图4可知,随着张力的增大不同纤维体积含量的纤维丝束带y向弹性模量Ey均增大。当纤维体积分数Vf≤50%时,张力引起的Ey变化值大于纤维体积分数引起的Ey变化值。当张力达到45N后曲线开始缓慢下降,当表面张力继续增大时,导致纤维磨损甚至断裂或树脂基体在纤维表面分布不均匀而导致弹性模量降低。Vf>50%时,张力引起Ey值的变化相对较小,当张力大于50 N后曲线逐渐趋于平缓。

由图5可知,张力F作用下不同纤维体积含量的纤维丝束带Ex、Ez的变化规律同Ey大致相同。不同之处在于随着张力F的不断增加,Ex、Ez表现出先逐渐增大而后趋于平稳,下降的幅度更为缓慢。

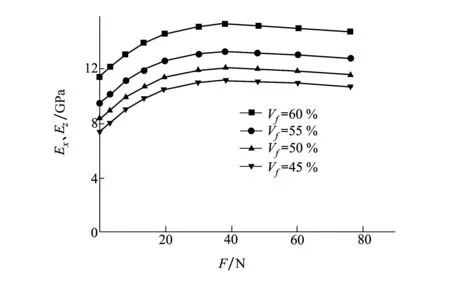
图5　纤维丝束带弹性模量Ex、Ez随张力的变化关系

图6和图7所示为张力F及纤维体积含量对剪切模量Gxy、Gzy、Gxy的影响规律。由图6可见,随着张力的增加各种纤维体积含量的纤维丝束带的剪切模量Gxz均逐渐增加,当张力到达40N左右时纤维丝束带剪切模量到达最大值,当张力继续增加时剪切模量Gxz将开始逐渐下降。另外,在同等张力的作用下纤维体积含量越高剪切模量Gxz下降的速率越缓慢。由图7可见,随着张力的增大Gzy、Gxy表现出先慢后快的上升趋势,并且纤维体积含量越高这种变化趋势越快。

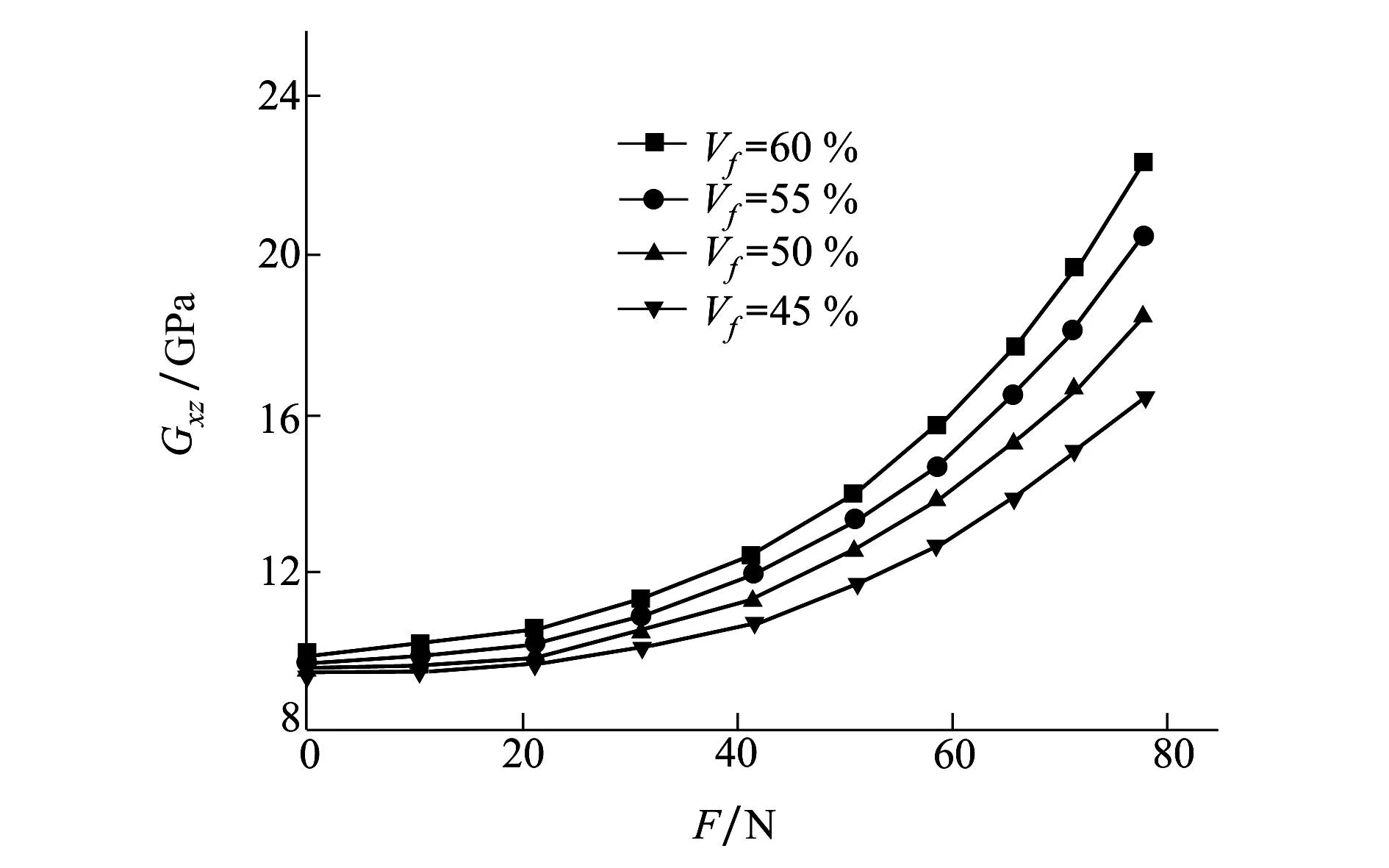
图6　纤维丝束带剪切模量Gxz随张力的变化关系

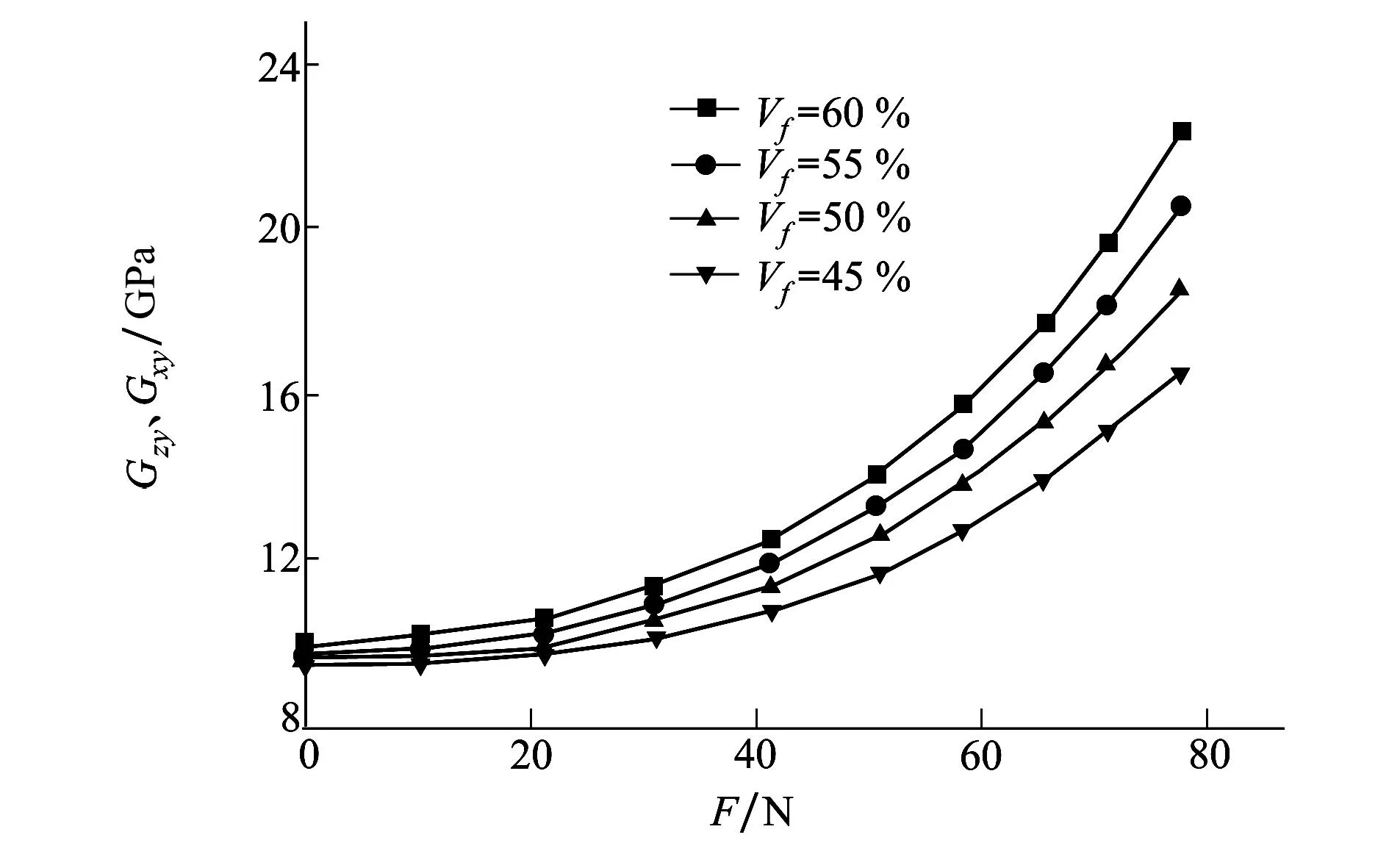
图7　纤维丝束带剪切模量Gzy、Gxy随张力的变化关系

3.2温度对纤维丝束带弹性性能的影响

温度对复合材料纤维丝束带性能的影响主要是由于在不同加热温度时树脂基体的性能以及树脂与纤维之间的结合特性会发生变化,从而影响纤维丝束带的性能。当丝束带加热温度较低时,树脂黏度高并不能完全充满与纤维之间的所有孔隙树脂分布均匀性较差,容易形成富胶区与孔隙从而导致性能降低。但随着加热温度的逐渐升高树脂开始充分浸入纤维与纤维之间,孔隙明显减少树脂分布均匀性增强无明显的富胶区域;当温度继续升高时树脂接近于完全融合状态,由于黏度太低流动性增强造成纤维与树脂的分布均匀性变差,纤维丝束带的性能由此降低。

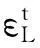
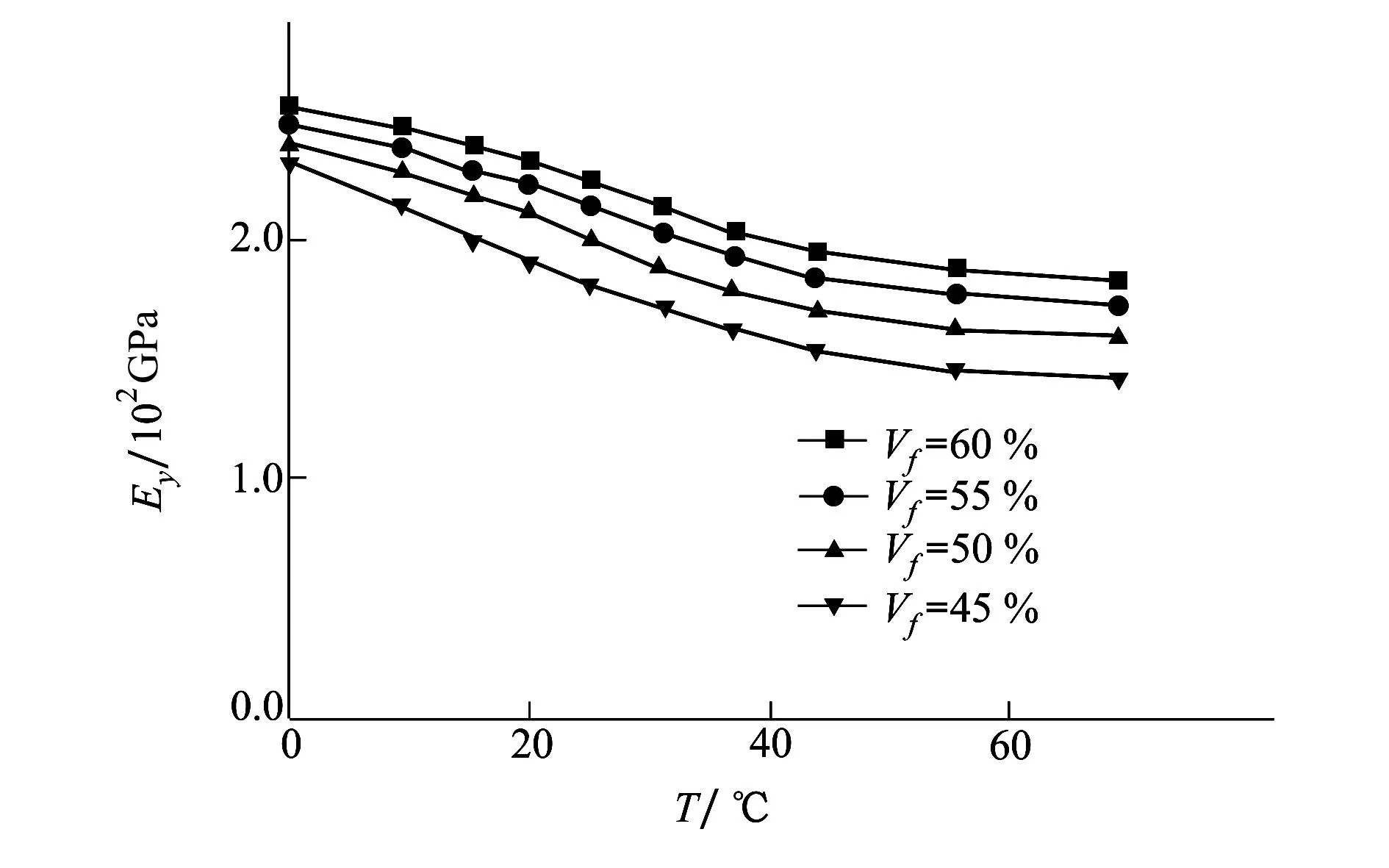
图8　纤维丝束带弹性模量Ey随温度的变化关系

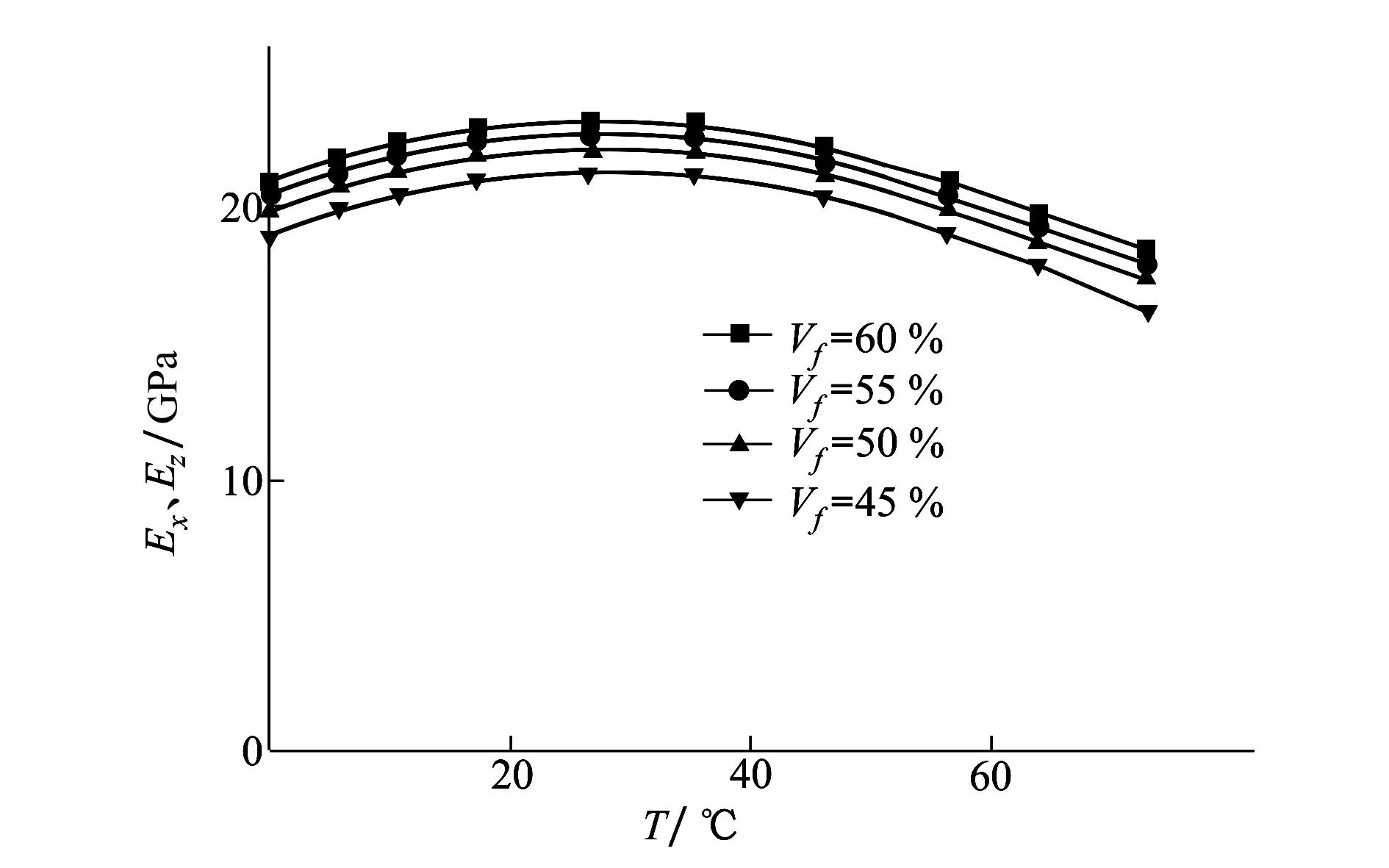
图9　纤维丝束带弹性模量Ex、Ez随温度的变化关系

从图8可以看出当温度升高时,不同体积分数的纤维丝束带的弹性模量Ey表现出先逐渐减小而后趋于稳定的变化规律,在相同温度作用下纤维体积含量越高弹性模量Ey的这种变化趋势越缓慢。这是由于在工艺温度作用下,树脂基体受温度的作用后状态转变而导致树脂基体的刚度下降,纤维相对于树脂基体受温度的影响较小。由图9可见,随着温度的不断升高Ex、Ez表现出现先增加后降低的变化规律。并且纤维体积含量越高这种变化也相应的越缓慢。这是由于温度在较低范围内变化时有利于树脂与纤维的充分浸润使得纤维丝束带整体刚度上升。

图10和图11所示为温度T及纤维体积含量对纤维丝束带剪切模量Gxz和Gzy、Gxy的影响规律。由图10可以看出,随着温度不断升高不同纤维体积含量的纤维丝束带剪切模量Gxz均逐渐降低。相同温

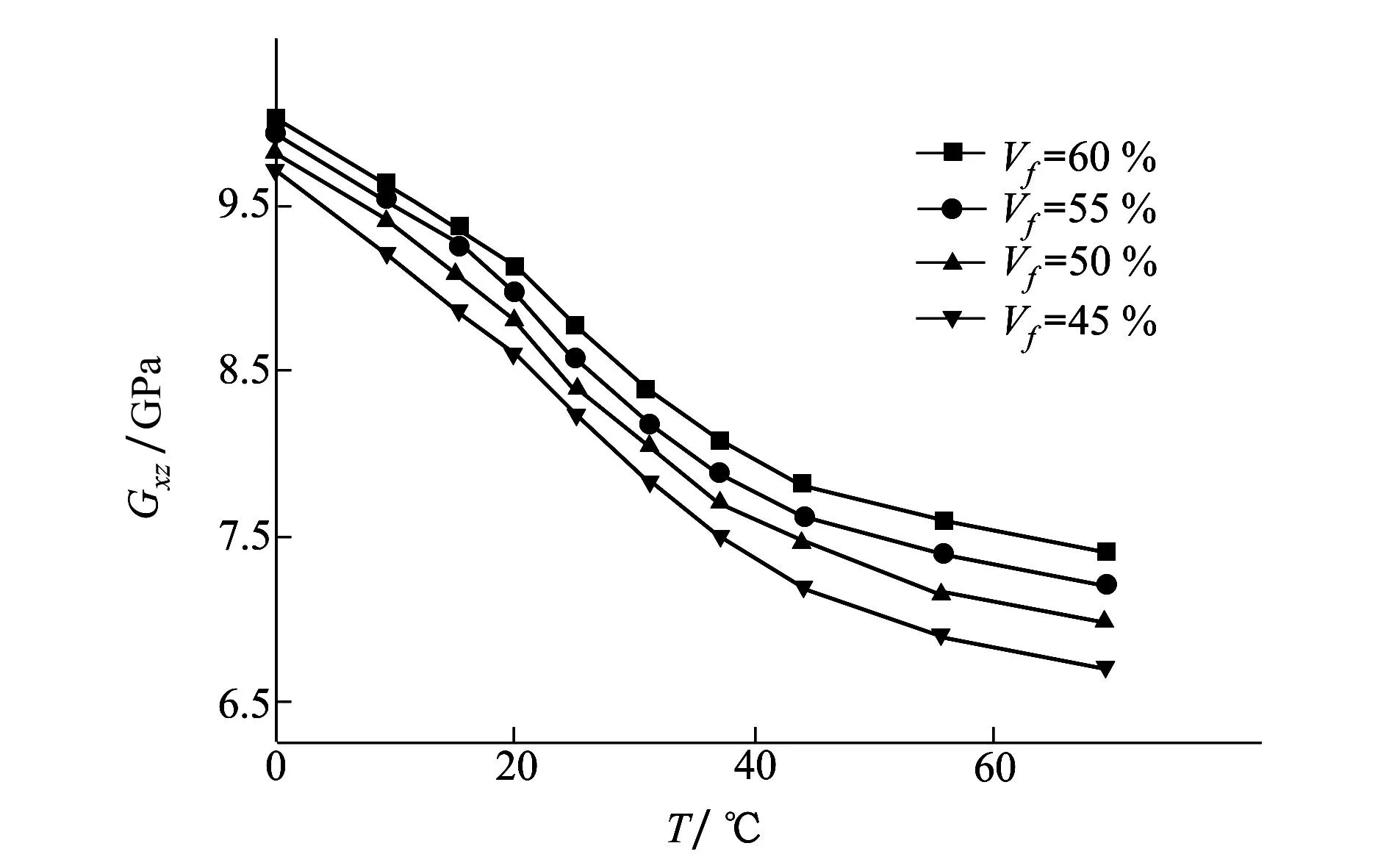
图10　纤维丝束带剪切模量Gxz随温度的变化关系

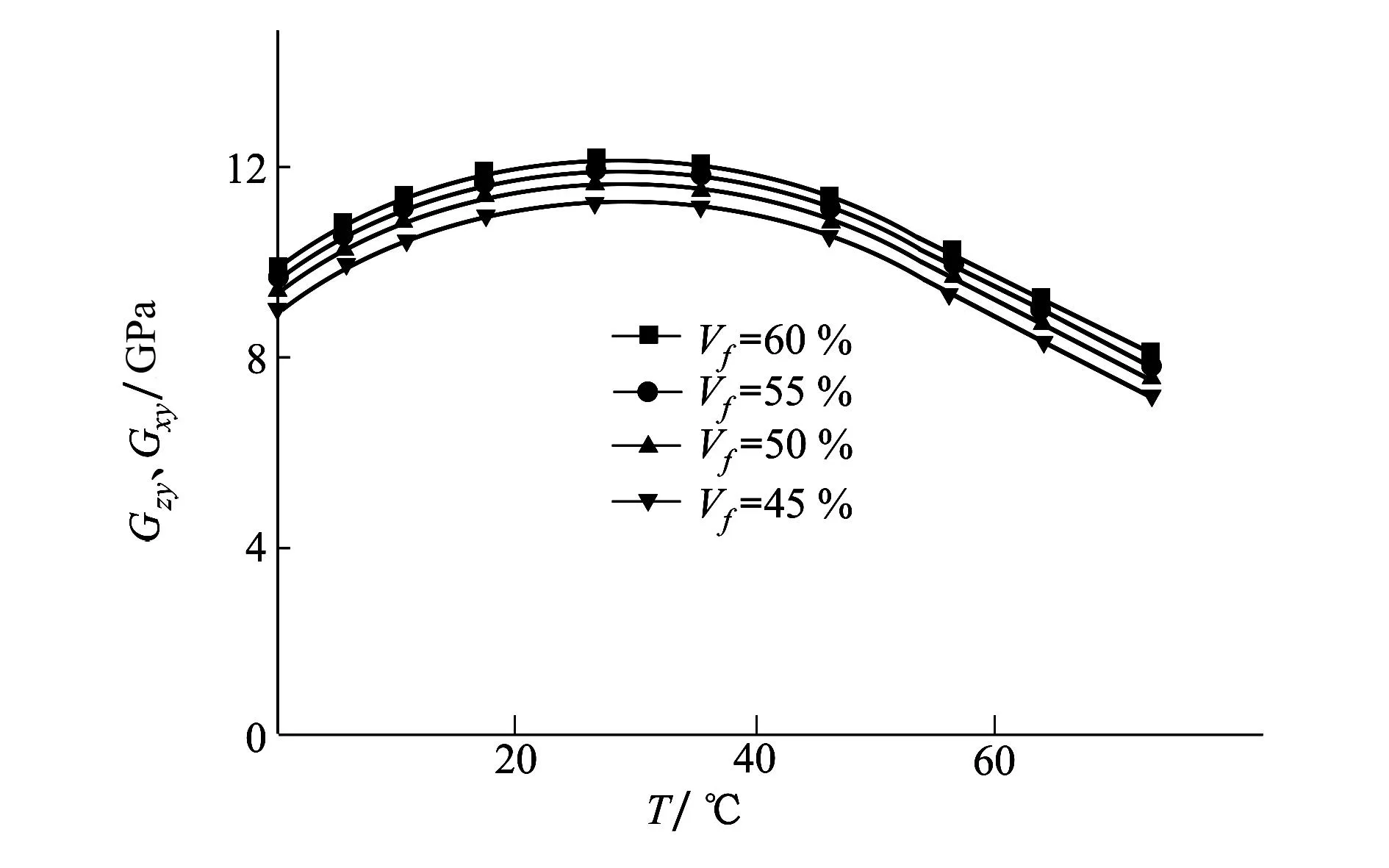
图11　纤维丝束带剪切模量Gzy、Gxy随温度的变化关系

度情况下,纤维体积含量越小剪切模量Gxz降低的速率越快。由图11可以看出,随着温度的升高纤维丝束带剪切模量Gzy、Gxy的幅值较Gxz有所下降外其他的变化规律与Gxz相同。

4结论

本文主要针对复合材料纤维丝束带成型过程所施加的工艺张力和温度对纤维丝束带弹性性能及热膨胀性能的影响规律进行了详细研究,利用ABAQUS有限元软件建立了纤维丝束带的参数化有限元模型,得到了弹性参数随张力、温度及纤维体积含量的变化规律。通过引入弹性参数的边界条件,对不同纤维体积含量的丝束带进行了仿真实验研究。研究结果表明:

1) 张力及温度都会引起纤维丝束带弹性参数和热物理参数的变化,随着张力在一定范围内的增大纤维体积含量增大,纤维丝束带的弹性参数均逐渐增大;

2) 随着温度的不断升高Ex、Ez表现出现先增加后降低的变化规律弹性参数缓慢的减小;而Ey则表现出先逐渐减小而后趋于稳定的变化规律。剪切模量除Gzy、Gxy的幅值较Gxz有所下降外其余变化规律相同。

参考文献：

[1]Kazem Fayazbakhsh, Mahdi Arian Nik, Damiano Pasini, et al. Defect Layer Method to Capture Effect of Gaps and Overlaps in Variable Stiffness Laminates Made by Automated Fiber Placement [J]. Composite Structures, 2013, 97: 245-251

[2]Mouritz A P, Feih S, Mathys Z, et al. Mechanical Property Degradation of Naval Composite Materials [J]. Fire Technology, 2011, 47(4): 913-939

[3]Nguyen Tiencuong, Zhao Xiaoling, Riadh Al-Mahaidi. Effects of Ultraviolet Radiation and Associated Elevated Temperature[J]. Composite Structures, 2012, 94: 3563-3573

[4]Mahmood Ansar, Wang Xinwei, Zhou Chuwei. Elastic Analysis of 3D Woven Orthogonal Composites[J]. Grey Systems: Theory and Application, 2011, 1(3): 228-239

[5]Xiao Hao, Lu Yonggen, Zhao Weizhe, et al. The Effect of Heat Treatment Temperature and Time on the Microstructure and Mechanical Properties of PAN-Based Carbon Fibers[J]. Journal of Materials Science, 2014 49: 794-804

[6]卢子兴, 王成禹, 夏彪. 三维全五向编织复合材料弹性性能及热物理性能的有限元分析[J]. 复合材料学报, 2013, 30(3): 160-167

Lu Zixing, Wang Chengyu, Xia Biao. Finite Element Analysis of Elastic Property and Thermo-Physical Properties of Three-Dimensional and Fullfive-Directional Braided Composites[J]. Acta Materiae Composite Sinica, 2013, 30(3): 160-167 (in Chinese)

[7]Yuan M N, Yang Y Q, Xia Z H. Modeling of Push-out Test for Interfacial Fracture Toughness of Fiber-Reinforced Composites[J]. Advanced Composite Materials, 2012, 21(5/6): 401-412

[8]Rodrígez M, Molina-Aluía J M, González C, et al. A Methodology to Measure the Interface Shear Strength by Means of the Fiber Push-in Test[J]. Composites Science and Technology, 2012, 72: 1924-1932

[9]Ghasemi Nejhad M N, Cope R D. Thermal Analysis of In-Situ Thermoplastic Composite Tape Laying[J]. Journal of Thermoplastic Composites Materials, 1991, 4:20-45

[10] Haktan Karadeniz Z, Dilek Kumlutas. A Numerical Study on the Coefficients of Thermal Expansion of Fiber Reinforce Composite Materials[J]. Composite Structures, 2007, 78(5): 1-10

[11] Rao M V, Mahjan P, Mittal R K. Effect of Architecture on Mechanical Properties of C/C Composites[J]. Composite Structures, 2008, 83(2): 131-142

[12] Ruiz E, Trochu F. Thermo Mechanical Properties during Cure of Glass-Polyester RTM Composites: Elastic and Viscoelastic Modeling [J]. Journal of Composite Materials, 2005, 39(10): 881-916

Finite Element Analysis Forming Process Parameters Influences on Elastic Properties of Fiber Reinforce Prepreg

Zhang Hongji1,2, Tang Hong1，Shi Yaoyao1

(1．Department of Mechanical Engineering，Northwestern Polytechnical University，Xi'an 710072，China 2．College of Energy Engineering，Yulin University，Yulin 719000，China)

Abstract:Based on the micro-structure of fiber reinforce prepreg composites, elastic deformation theory of fiber reinforce prepreg was derivation under the action of process tension and temperature parameters. Using finite element analysis software established the parameterization finite element model. By applying reasonable load and boundary condition, to study the changes of the elastic properties parameters of the fiber reinforce prepreg under the action of tension and temperature. On the basis of discuss the relationship between tension and fiber volume content, detailed analysis the influence of the tension, temperature and fiber volume content on elastic properties of fiber reinforce prepreg. The results show that: with the increase of tension in range of 0～50 N, elastic modulus and shear modulus are presented as approximate linear increase and then remained stable last decreased, and the shear modulus is trend slower. With the temperature increasing, longitudinal modulus of fiber reinforce prepreg showed gradually decreased and then tends to be steady, and the higher the fiber volume content, the change trend slower. The transverse modulus of show firstly increases and then decreases. The shear modulus decreases with the increase of temperature.

Keywords:composites; elastic property; fiber reinforced prepreg; process parameters

中图分类号：TB332

文献标志码：A

文章编号:1000-2758(2016)01-0132-07

作者简介：张宏基(1983—),西北工业大学博士研究生，主要从事复合材料缠绕铺放成型工艺及装备控制技术研究。

基金项目：国家自然科学基金面上项目(51475377、51375394)资助

收稿日期：2015-09-12