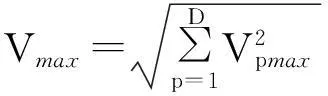基于混合策略的UCAV攻击轨迹在线规划方法

董康生, 黄长强, 黄汉桥, 曹林平, 唐传林

(空军工程大学 航空航天工程学院, 陕西 西安　710038)



基于混合策略的UCAV攻击轨迹在线规划方法

董康生, 黄长强, 黄汉桥, 曹林平, 唐传林

(空军工程大学 航空航天工程学院, 陕西 西安710038)

摘要：针对无人作战飞机(unmanned combat aerial vehicle,UCAV)在线轨迹规划问题,提出了一种基于混合策略的方法。首先,针对动态不确定环境,设计了基于事件触发的轨迹滚动规划方案;其次,基于UCAV飞行性能约束对数字地形进行平滑处理,生成安全可飞行曲面;再次,提出了利用函数表征重规划段轨迹的方法,分析了轨迹函数特性和端点约束处理方法,进而将轨迹规划问题转化为轨迹函数寻优问题,减少了轨迹寻优参数数量;最后,引入平均速度和FUCH混沌映射对粒子群算法进行改进,并利用其对轨迹函数进行寻优。数字仿真结果表明,利用该方法完成一次轨迹在线重规划只需0.2 s,表明了该方法具有较好的实时性,能满足轨迹在线规划要求。

关键词：UCAV;轨迹在线规划;滚动优化;轨迹函数寻优;混沌粒子群算法

无人作战飞机自主攻击技术是未来发展的必然趋势和迫切需要,而攻击轨迹在线实时重规划技术是实现自主攻击的关键。国内外学者对轨迹规划问题进行了大量研究并形成了很多方法[1-3],这些方法可分为2类:①最优控制法:将轨迹规划问题转化为包含微分方程、代数方程和不等式约束求解泛函极值的开环最优控制问题,再利用解最优控制的方法来解算最优攻击轨迹,文献[1]采用了这类方法。②可以概括为空间直接法:利用特定算法(A*算法、粒子群算法、进化算法、概率路图法、随机决策树法等)直接在轨迹规划空间搜索最优攻击轨迹点,然后将这些轨迹点连接起来构成攻击轨迹,文献[2-3]采用了这类方法。

最优控制法能考虑复杂的飞行约束和环境约束、解算参数全、精度高,但耗时长,难以满足在线规划的要求;空间直接法源于机器人路径规划思想,直接在轨迹规划空间进行最优轨迹的搜索,算法简洁、解算速度快,但解算精度不高,且若将其直接应用到三维空间的攻击轨迹寻优会存在求解参数多而导致的计算量非常大的问题,难以满足实时性要求。对数字地形进行平滑化处理使其满足飞行器性能约束要求,从而生成安全可飞行曲面[3],然后在该曲面上进行轨迹规划,由于该曲面上的轨迹与它的平面投影一一对应,因而可将UCAV三维轨迹规划问题转化为二维平面轨迹规划问题。同时,滚动时域优化方法以其突出的应对动态不确定性的优势,得到了广泛应用[4],是解决实时规划问题的重要途径。

基于以上分析,本文设计了一种基于混合策略的轨迹在线规划方法,论文的主要内容包括:(1)在线轨迹规划问题分析与建模;(2)设计攻击轨迹滚动规划策略和方法,使UCAV能有效应对动态不确定环境;(3)提出一种新的轨迹表示方法,并将轨迹规划问题转化为轨迹函数寻优问题;(4)设计一种的改进混沌粒子群算法并利用其对轨迹函数参数进行寻优,生成最优攻击轨迹。

1在线轨迹规划问题分析与建模

1.1动态环境因素分析

UCAV在执行任务飞行过程中会遇到很多动态变化因素,这些变化因素主要包括:

1) 战场环境的不确定性,详细的环境参数信息很难预先准确获知,如天气变化、地理条件等;

2) 情报信息的不准确性,情报的获取、编译和传递过程会出现误差以及受到复杂电磁环境的干扰;

3) 威胁的机动和敌方探测系统的机动,甚至还有作战任务的变更;

4) 敌方战略、战术意图的变更。

因为有这些动态不确定因素,为确保任务的有效完成,UCAV必须要具有轨迹实时重规划的能力。

1.2UCAV数学模型

轨迹规划只需要轨迹点的空间位置即可,为此采用UCAV三自由度模型[4]。

UCAV在惯性坐标系下的质点运动方程为:

(1)

UCAV在航迹坐标系下的质点动力学方程为:

(2)

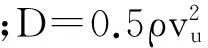
1.3动态威胁模型

1.3.1地面威胁建模

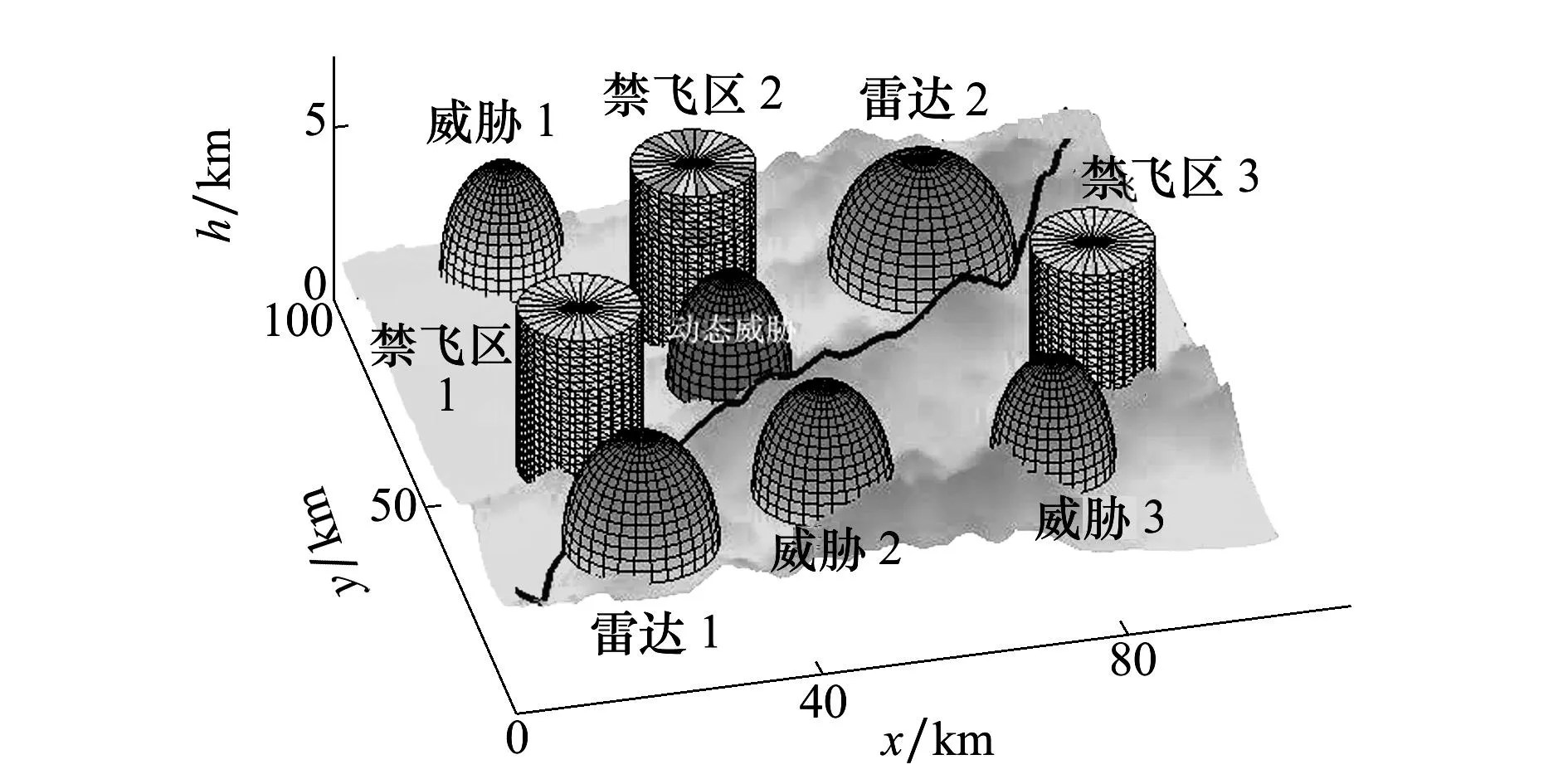
地面威胁主要有防空武器和防空雷达威胁。通用做法是将防空武器(雷达)等效为一个半球形杀伤区(威胁区),半径大小与武器威胁程度或雷达探测能力成正比。

地面威胁模型函数:

式中:x0、y0、h0为武器(雷达)坐标位置,R为武器杀伤(雷达探测)半径。令x0=20km,y0=20km,h0=0km,R=10km得到地面威胁模型,如图1所示。

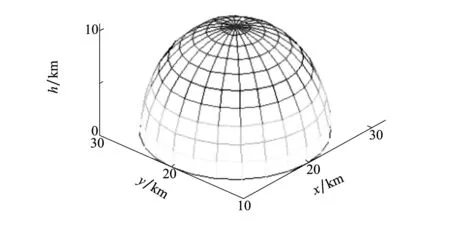
图1　地面威胁模型

1.3.2禁飞区模型

UCAV飞行中可能会遇到有恶劣气象环境的区域或者政治、军事敏感区,这些区域是禁止飞行的区域,即禁飞区,UCAV不能从其上方飞行,因而可将禁飞区简化为高度很大的圆柱形。以半径r=10 km为例,建立禁飞区模型如图2所示。

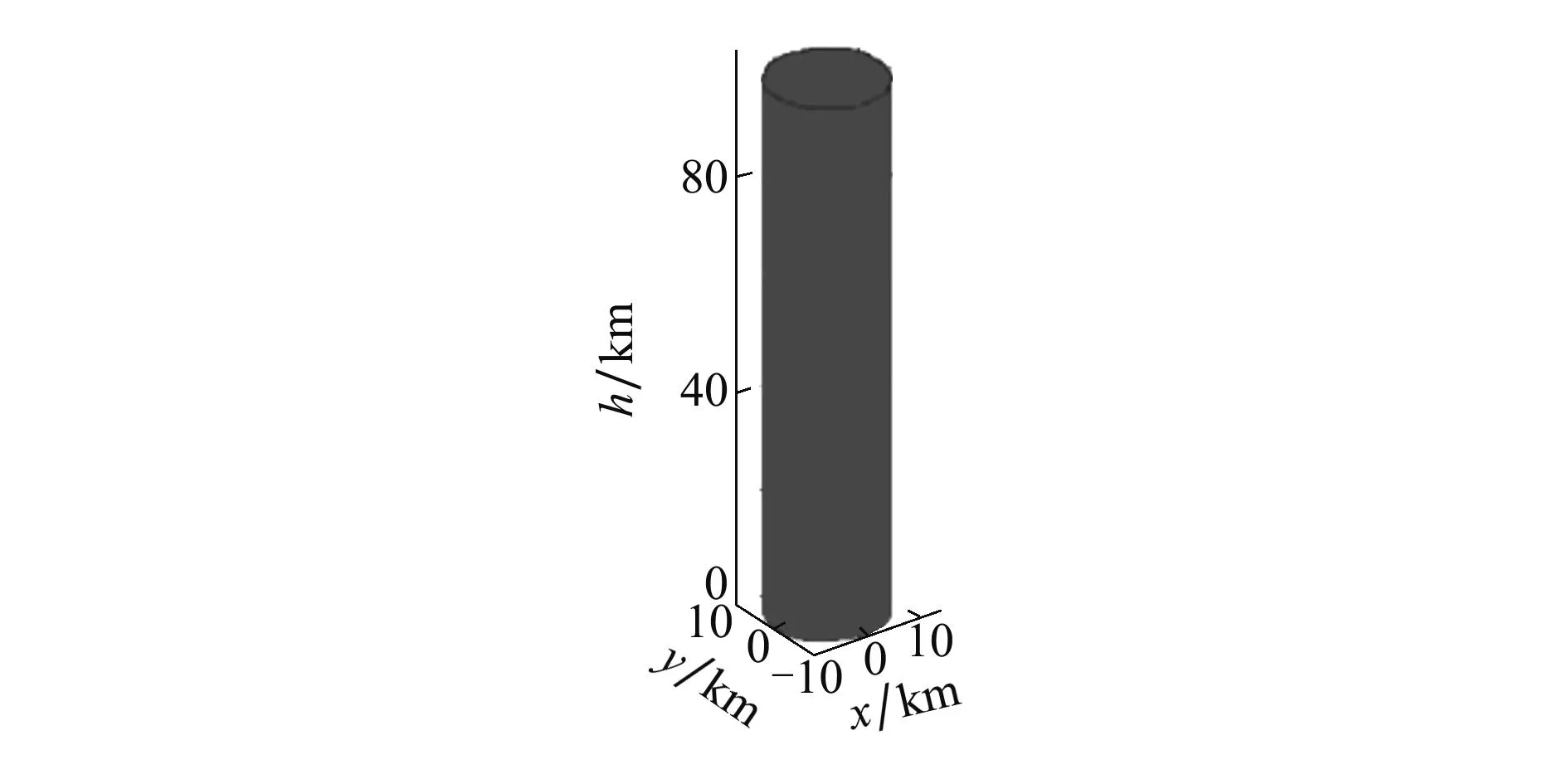
图2　禁飞区模型

1.4数字高程模型

采用由美国太空总署(NASA)和国防部国家测绘局(NIMA)联合测量的SRTM数据,选取精度为90m 、编号为N33E069的数字地形,如图3所示。

图3　DEM数字地形

1.5轨迹在线重规划问题优化目标函数

首先,在轨迹规划中我们总是希望UCAV的总航程最短,以节省油耗和时间,占据有利态势。构建航程代价:

其次,鉴于UCAV自卫能力较差,不能进入威胁区或禁飞区,对进入威胁区或禁飞区的轨迹给予一个很大的惩罚值。即:

(3)

式中,下标“Thr,i”表示第“i”个地面威胁,下标“Forb,j”表示第“j”个禁飞区。“M”是一个值很大的正常数。

最后,构建总目标函数为:

(4)

式中,α∈[0,1]为权系数。

2UCAV轨迹在线滚动规划方法

2.1安全可飞行曲面生成技术

根据UCAV最大爬升角约束、飞行速度约束以及过载约束来确定地形的坡度约束和曲率约束,进而利用这些约束来修正高程,达到平滑地形的效果。地形平滑处理结果如图4所示。

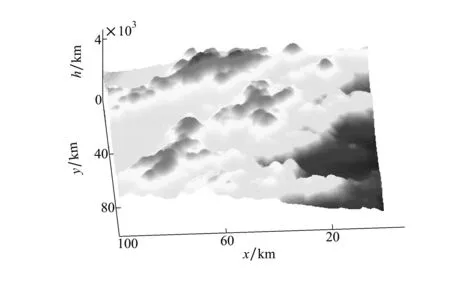
图4　平滑处理后的数字地形

2.2滚动时域优化策略

滚动时域优化方法源于预测控制优化原理,把整个任务过程分为一个个相互重叠且不断向前推进的优化区间(这个优化区间也称为滚动窗口),用在线滚动进行的有限时段局部优化取代一成不变全局优化。

轨迹重规划只会在遇到突发威胁、目标机动或任务变更等情况时才会进行,即是由事件触发的,因而本文采用事件触发式滚动机制。

首先,定义轨迹滚动规划触发事件:

1) 在飞行轨迹周边出现突发威胁,且按原轨迹飞行会有较大安全威胁;

2) 出现新的更高价值目标;

3) 先验的战场环境信息出错或者作战区域战场环境发生较大变化,预先精细规划的轨迹不能执行;

4) 目标进行了大机动,预先规划轨迹终点偏离目标较远;

5) 任务取消或更改为执行其他更加紧迫的任务。

其次,设计重规划区域大小、轨迹起点位置、终点位置和终点进入角确定方法。轨迹滚动规划过程示意图如图5所示。

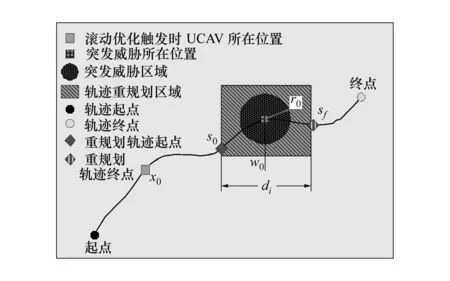
图5　轨迹滚动规划过程示意图

1) 重规划区域大小定义方法。UCAV根据作战任务、计算能力和存储能力的不同选择合适的梯度类型,例如定义梯度Δd=10 km,则区域大小为d1=10 km,d2=20 km,d3=30 km,d4=40 km;

2) 重规划区域大小选择方法。假设威胁点位置为w0,威胁作用半径大小为r0;轨迹滚动优化触发时UCAV所在位置为x0,飞行速度为v0,轨迹重规划解算时间为τ。则重规划区域长度di由(5)式确定:

(5)

式中,Δd为安全距离。

3) 重规划轨迹起点位置s0和终点位置sf的确定。

如果x0+v0·τ≤w0-di/2,则s0=w0-di/2,

sf=s0+di;

如果x0+v0·τ>w0-di/2,则s0=x0+v0·τ,

sf=s0+di。

4) 确定终点进入角。轨迹终点进入角则由轨迹终点所在位置的曲率决定。记终点所在位置的曲率为ρ=f′(x,y),则轨迹终点进入角λ=tan-1ρ。

轨迹在线滚动规划详细过程:

step1UCAV实时综合传感器探测信息和数据链信息,判断触发事件是否发生,如果发生,则执行轨迹重规划程序,转入step2;否则,重复step1;

step2UCAV根据其飞行性能、突发威胁的大小特征或目标位置变动情况,快速确定重规划区域长度、轨迹起点位置、终点位置和终点进入角,转入step3;

step3进行重规划轨迹的快速解算,转入step4;

step4UCAV按照重规划轨迹飞行,若到达目标攻击位置,则终止优化,否则返回step1。

2.3轨迹函数特性及端点约束处理

2.3.1轨迹函数特性研究

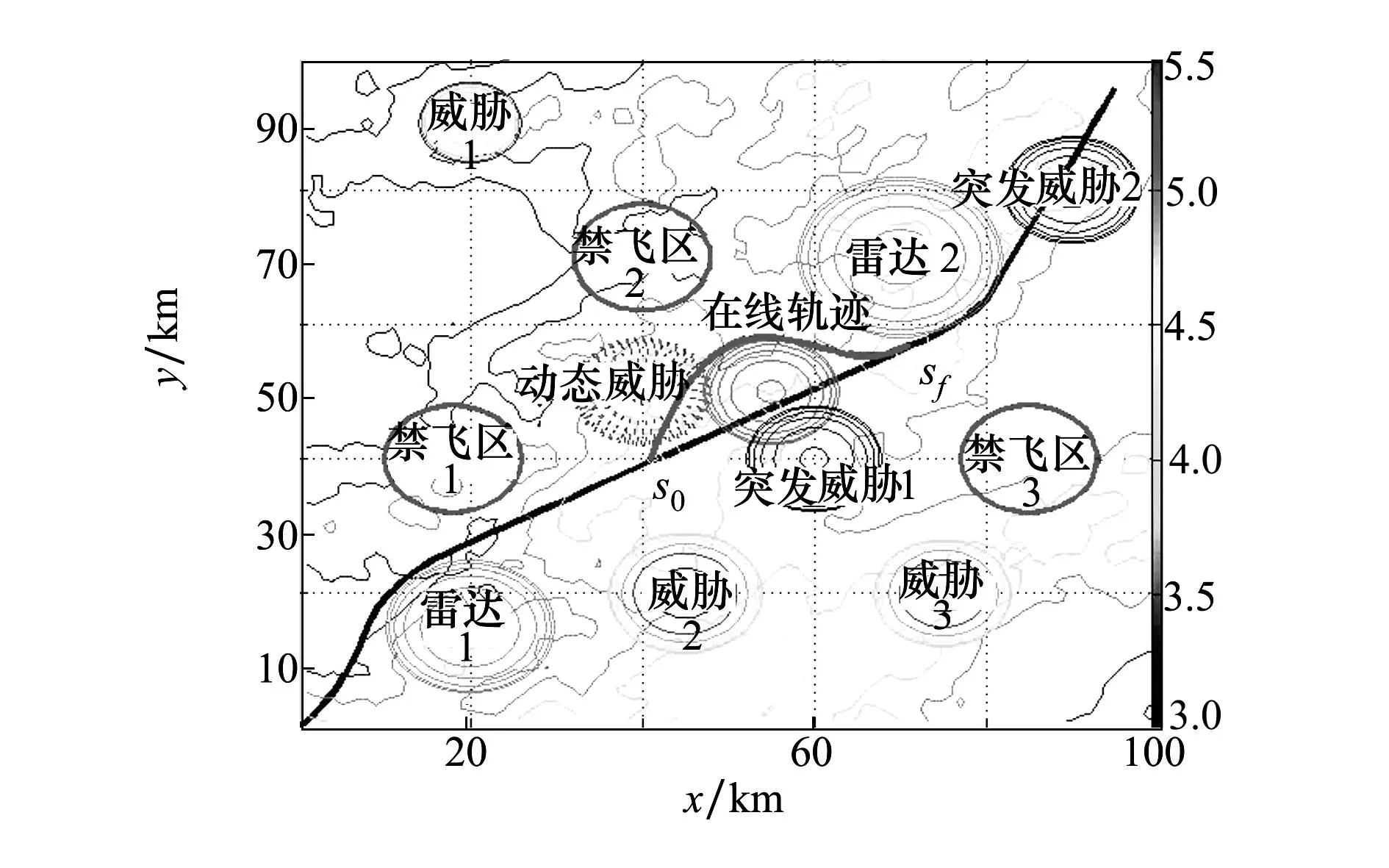
轨迹实时重规划是因为突发威胁的出现而对受到威胁的轨迹段进行重新规划,因而轨迹实时重规划是小范围的轨迹规划问题,一般为10～30 km。

考察多项式函数:

(6)

由该多项式函数易知,a0决定了轨迹的起始位置,a1决定了轨迹的起始斜率。

2.3.2轨迹端点约束处理

轨迹重规划修正的起点和终点由威胁特性、滚动策略和UCAV自身性能决定。规划出的轨迹必需能满足起点、终点位置约束和终点进入角约束,也就是说轨迹函数必须要满足起点、终点位置约束和终点的斜率约束。

以n=4为例进行分析,由轨迹起点、终点位置和终点进入角约束易得:

(7)

式中,下标“f”表示末端位置参量,下标“0”表示起点位置参量,l为末端进入角(斜率)。

以a3、a4为自变量,a1、a2为因变量,解(7)式方程得:

(8)

由(8)式知,只要给出轨迹的初始和终端约束条件y0、yf、l,轨迹曲线就可由a3、a4共同确定。

由此,复杂的轨迹优化问题就转化为了寻找2个最优参数的问题,问题得到了极大简化。下文将设计一种改进的粒子群算法对该参数进行寻优。

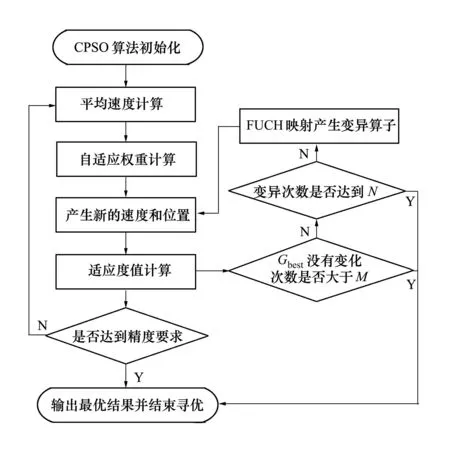
2.4改进的混沌粒子群优化算法

2.4.1基本粒子群算法

粒子群优化算法(PSO,particle swarm optimization) 由Kenney和Eberhart于1995年提出,是一种模拟鸟类捕食行为的群智能全局优化算法[5]。群体中的粒子在每次迭代搜索过程中,通过跟踪2个极值:粒子本身找到的个体最优解Pbest和群体找到的全体最优解Gbest来调整自己速度和位置,完成对问题的寻优。

每个粒子的速度和位置按如下公式进行更新:

(9)

式中:d∈[1,D],i∈[1,N],c1、c2为学习因子,通常c1=c2=2,rand1、rand2为[0,1]之间的随机数,0

基本PSO算法容易早熟而不能有效找到最优解,为此将利用混沌映射对PSO算法进行改进,构建混沌粒子群算法(CPSO)。

2.4.2Fuch混沌映射特性分析

混沌是非线性系统中的一种普遍现象,混沌现象行为复杂且类似随机,但存在精致的内在规律性和遍历性。混沌搜索已经成为一种新颖的全局优化技术[6]。传统混沌映射主要有Logistic映射、Tent映射和Chebyshev映射。傅文渊等[7]提出了一种新的无线折叠混沌映射——Fuch映射,Fuch映射具有很多特殊的优点。

Fuch映射方程:

(10)

式中,x≠0。

2.4.3改进的混沌粒子群算法

利用Fuch混沌序列进行粒子的初始化,加强粒子对其邻域快速搜优,改善了算法的随机性,有助于提高寻优效率和精度。并以Fuch混沌序列代替随机数对粒子的速度、位置进行更新。粒子群搜索的中后期进行粒子停滞判断与粒子变异操作。线性变化权重不能反映粒子的收敛性,为此引入平均速度对自适应权重进行改进。具体方法如下:

1) 自适应权重的改进

定义平均速度:

(11)

Vip(k)为第i个粒子的p维速度。

粒子搜索的早期是全局搜索期,平均速度很大,是活跃阶段;随着搜索次数的增加粒子趋于最优,粒子进入局部搜索阶段,平均速度很小,最终速度趋于零。因而,平均速度是粒子活跃性或者算法收敛性的特征之一。通过平均速度重新定义自适应惯性权重。惯性权重

(12)

粒子搜索早期,全局最优并不是真的最优,个体最优则扮演者更加重要的角色;粒子收敛后期,全局最优的作用应该突出,个体最优减弱。因而,c1应该先大后小,c2应该先小后大。结合平均速度的概念重新定义c1、c2如下:

(13)

式中,C为常数。

2) 停滞判断与粒子变异方法

平均速度的应用能够改善算法的收敛性,减少总迭代次数,但也会使粒子更易陷入局部最优,因而需要对陷入局部最优的粒子进行判断和干预,使其跳出局部最优,从而加强算法的全局最优性。

改进的CPSO算法具体流程见图6所示。

图6　改进的CPSO算法流程图

3仿真与分析

3.1UCAV三维轨迹预先精细规划

在第2节生成的安全可飞行曲面上叠加等效为地形高程的地面防空威胁和禁飞区,进而生成综合威胁的安全可飞行曲面,然后利用HP自适应伪谱法进行攻击轨迹预先精细规划。仿真条件:计算机配置为1.99 GHz,内存4G,CPU为Inter Core2双核;UCAV起点坐标(0,0,3.5),终点坐标(95,95,3),地形威胁主要有雷达威胁、防空火力威胁、禁飞区约束以及动态威胁,其中机动防空火力单元的当前坐标为(40,50,2.6)。为凸显地形特征,在图形的显示上对高程进行了压缩,具体分布及轨迹规划结果如图7、图8所示。

图7　轨迹三维视图

图8　轨迹等高线图

仿真结果表明HP自适应伪谱法能精确的规划出满足约束条件的攻击轨迹,但仿真用时3 min,难以满足在线实时规划的要求。

3.2突发威胁下轨迹在线实时重规划

UCAV按照预先规划的精细轨迹飞行,并根据设计的滚动规划策略进行轨迹实时在线重规划。UCAV在坐标(30,33,5.3)处综合探测信息判断机动防空火力单元正向东以100 m/s速度机动,并在坐标(60,40,2.5)和坐标(90,80,2.7)出现杀伤半径为8 km的突发威胁,预先规划轨迹受到威胁,启动轨迹滚动重规划程序。

将威胁条件代入滚动规划程序解算得到重规划区域大小di=30,起点坐标为(41,40,2.8),终点坐标为(71,57,3.6),终点进入角λ=40°。

利用改进的CPSO算法进行轨迹实时在线重规划。仿真比较了标准PSO算法与改进的CPSO算法的解算结果,仿真结果如图9、图10所示。

图9　在线轨迹三维视图

图10　在线轨迹等高线图

3.3仿真结果分析

利用改进的CPSO算法进行轨迹在线重规划所需时间不到0.2 s,而标准PSO算法需要0.8 s左右,表明算法具有很好的实时性。从规划结果来看,重规划轨迹有效躲避了突发威胁,轨迹平滑且很好地与预先规划轨迹在端点平滑衔接,易于飞行控制。综上表明,该算法能快速实时规划出UCAV三维可飞行轨迹。

4结论

针对轨迹在线实时重规划问题,提出了一种基于滚动策略的轨迹规划方法。设计了轨迹滚动规划策略和详细方案,使UCAV有效应对动态变化环境,并结合安全可飞行曲面生成技术,将三维轨迹规划问题转换为二维轨迹规划问题,大大减小了问题的复杂度;创新性地提出了多项式函数表示轨迹的方法,将轨迹规划问题转化为轨迹函数寻优问题,减少了优化参数数量,并研究了轨迹函数特性和端点处理方法,研究表明轨迹函数能很好地处理端点约束问题;通过引入平均速度和FUCH混沌映射对粒子群算法惯性权重与停滞粒子进行改进,提高了算法的收敛性和全局最优性,并利用其对轨迹函数进行寻优。仿真结果表明,用该方法完成一次轨迹在线重规划只需0.2 s,表明了该算法具有很好的实时性和实用性。

参考文献：

[1]Darby C L, Hager W, Rao A V. Direct Trajectory Optimization Using a Variable Low-Order Adaptive Pseudospectral Method[J]. Journal of Spacecraft and Rockets, 2011, 48(3): 433-445

[2]Li Pei, Duan Haibin. Path Planning of Unmanned Aerial Vehicle Based on Improved Gravitational Search Algorithm[J]. Science China Technological Sciences, 2012, 55(10): 2712-2719

[3]唐强, 张新国, 刘锡成. 一种用于低空飞行的在线航迹重规划方法[J]. 西北工业大学学报, 2005,23(2): 271-275

Tang Qiang, Zhang Xinguo, Liu Xicheng. Exploring an Online Method of Vehicle Route Re-Planning for Low Altitude Flight[J]. Journal of Northwestern Polytechnical University, 2005, 2005,23(2): 271-275 (in Chinese)

[4]Carole G Prevost, Olivier Theriault, Andre Desbiens. Receding Horizon Model-Based Predictive Control for Dynamic Target Tracking: a Comparative Study[R]. AIAA-2009-62681

[5]Xiao Hongfeng, Tan Guanzheng. A Novel Particle Swarm Optimizer without Velocity: Simplex-PSO[J]. Journal of Cent South Univ Technol, 2010, 17: 349-356

[6]Lu Huijuan, Zhang Huoming, Ma Longhua. A New Optimization Algorithm Based on Chaos[J]. Journal of Zhejiang University Scienace A, 2006, 7(4): 539-542

[7]傅文渊, 凌朝东. 自适应折叠混沌优化方法[J]. 西安交通大学学报, 2013,47(2):33-38

Fu Wenyuan, Ling Chaodong. Adaptive Iterative Chaos Optimization Method[J]. Journal of Xi′an Jiaotong University, 2013, 47(2): 33-38 (in Chinese)

Online Planning Method for UCAV Attack Trajectory Using Multi-Strategies

Dong Kangsheng, Huang Changqiang, Huang Hanqiao, Cao Linping, Tang Chuanlin

(Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi′an 710038, China)

Abstract:A trajectory online planning method using multi-strategies is proposed for UCAV. Firstly, to copy with dynamic and changeable environment, we design an event triggered trajectory rolling planning program. Secondly, according to UCAV flying bounds, a safe and flyable curve generating method is designed by smoothing on digital geographical map. Thirdly, make use of function to replace with re-planning trajectory, analyze trajectory function speciality and terminal point handling methods, translating trajectory planning problem to trajectory function optimal problem; this reduces the number of optimal parameters. Lastly, we improve particle swarm optimization on its inertia weight and stagnant particles by introducing average speed and FUCH chaos mapping; this improves its convergence and global optimality; then we make use of the improved method to search for optimal trajectory function. Results of simulation show that the method proposed by us accomplishes an online trajectory re-planning in only 0.2s; clearly our method meets the requirements of trajectory online re-planning with its good real-time ability.

Keywords:UCAV, trajectory online planning, rolling planning, trajectory function optimization, chaotic PSO

中图分类号：V279

文献标志码：A

文章编号:1000-2758(2016)01-0159-07

作者简介：董康生(1988—)，空军工程大学博士研究生，主要从事无人作战飞机自主空战、轨迹优化的研究。

基金项目：国家自然科学基金(71501184)资助

收稿日期：2015-04-24