考虑J2项摄动的空间共振轨道特性分析

吝琳, 方群

(1.西北工业大学 航天学院, 陕西 西安　710072; 2.航天飞行动力学技术国家级重点实验室, 陕西 西安　710072)



考虑J2项摄动的空间共振轨道特性分析

吝琳1,2, 方群1,2

(1.西北工业大学 航天学院, 陕西 西安710072; 2.航天飞行动力学技术国家级重点实验室, 陕西 西安710072)

摘要：共振轨道是建立在新型坐标系下的非开普勒轨道,应用于空间机动轨道的设计,具有节省能量的优势。针对地球形状摄动J2项对共振轨道特性的影响分析问题,建立了一种新的考虑J2项摄动影响的共振轨道数学模型。通过与传统受J2项摄动影响的共振轨道数学模型的仿真对比分析可以看出,新的数学模型虽然形式较为复杂,但却能够揭示不同阶段J2项摄动使系统产生偏差的原因,比传统模型更为精确,因此更适用于工程实际中分析J2项摄动对共振轨道特性的影响。

关键词：非开普勒运动;共振轨道;J2项摄动

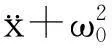
史格非[3]通过研究与仿真,一方面,说明共振轨道的推力峰值远小于应用Lambert转移时所需的最小速度增量;另一方面,肯定了共振轨道在星际探测应用中的可行性,并且证明了其在能量消耗方面优于Lambert轨道。陈诗瑜引入J2摄动和新的类Sundman转换关系,推导了参数平面下含J2摄动的空间共振轨道方程及转换矩阵,并分析了摄动因素对轨道特性的影响。下文中,我们将陈诗瑜推导所得数学方程称为传统数学模型,简称传统模型。

然而,文献[3]在进行模型建立时并未考虑摄动因素对轨道的影响。而传统模型虽然考虑了J2项摄动力对轨道的影响问题,但在建立数学模型时,忽略了J2项摄动内所含的位置矢量r,而将J2项摄动看做标量,这样所得结果不是很精确。

针对上述问题,本文在传统模型的研究基础上,利用KS变换,将J2项摄动看做矢量,考虑其所含位置矢量r对轨道特性的影响,建立一种新的考虑J2项摄动影响的共振轨道数学模型,随后，采用本文提出数学模型,进行了J2摄动因素对轨道特性影响的仿真分析,并与传统模型的仿真结果进行比较,结果表明:2种受摄共振轨道模型的仿真结果变化趋势相同,但由于所考虑的影响因素有所不同,因而导致偏差的具体变化程度不同;另外,由于考虑了J2项摄动方向对轨道特性的影响,本文所建立的模型比传统模型更为精确,更适用于工程实际中分析J2项摄动对共振轨道特性的影响。

1受J2项摄动影响的传统共振轨道建模

地球是一质量分布不均匀、形状也不规则的椭球体,这使得航天器在轨运行时,不仅受到径向引力的作用,在轨道的切线和法线方向也会受到摄动力的作用,这些附加的切向、法向力因素统称为地球形状摄动。

地球引力场位函数的一般表达式见(1)式:

(1)

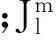
若只考虑J2项摄动,则位函数可简化为:

(2)

航天器在中心引力,J2摄动力和推力作用下的非开普勒运动微分方程为:

(3)

通过定义新的时间尺度和轨道描述参数,将(3)式中物理平面地心赤道坐标系下航天器的运动微分方程,经过数学变换,可以改为参数平面内的受迫振动方程。

传统模型在推导过程中,忽略了fJ2的方向,将其看做标量进行推导,得到的结果为:

(4)

式中,M为转换矩阵:

(5)

q为参数平面内的推力加速度,称为准推力加速度。取q为简谐振动信号,则有

(6)

由(4)式和(6)式可以看出,当准推力加速度q各分量的频率与固有频率一致时,即可产生共振。

2考虑J2项摄动方向影响的共振轨道建模

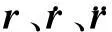
航天器在中心引力、J2项摄动力和推力作用下的非开普勒运动微分方程如(3)式所示。引入新的时间尺度广义偏近点角s,其与物理时间t的关系为

(7)

则有

(8)

(9)

y=2(u1u2-u3u4)

z=2(u1u3+u2u4)

(10)

(11)

式中

(12)

另一方面,根据KS变换的性质有:

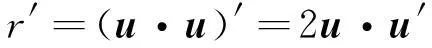
(13)

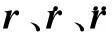
(14)

将(14)式等号左右两边左乘LT(u)整理得:

(15)

(15)式即为考虑J2项摄动方向影响的新型共振轨道数学模型。可以看出,考虑fJ2中所含的矢量r之后所建立的模型中,fJ2被分为两部分,一部分对系统固有频率ω0产生干扰,另一部分对连续小推力产生干扰,从而使轨道偏离目标位置,产生偏差。

为进一步了解J2项摄动对系统频率的影响,假设(15)式中J2项摄动对推力的影响为零,得到新的数学模型为

(16)

为方便起见,我们称(15)式为受摄共振轨道模型,称(16)式为频率受摄的共振轨道模型。对(15)式进行仿真所得的航天器位置偏差称为整体偏差,对(16)式进行仿真所得的航天器位置偏差为局部偏差。

3仿真分析

本文采用(15)式为数学模型,针对J2项摄动因素对共振轨道特性的影响进行分析。为比较方便,仿真初始参数与传统模型仿真时所取参数相同,具体数值如表1和表2所示,参数平面下推力加速度q的形式如(6)式所示。

表1　初始轨道根数

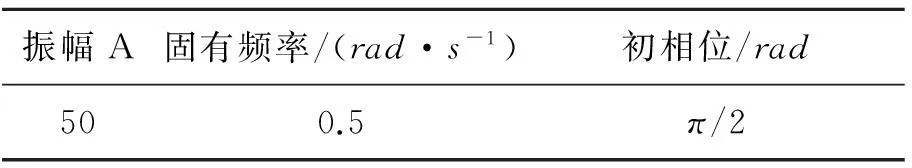
表2　推力加速度的初始参数

仿真结果如图1～图6所示:

图1和图2分别为(u1,u3)和(u3,u4)参数平面内的轨道图像。可以看出,在J2项摄动影响下,(u1,u3)参数平面内的受摄共振轨道与理想共振轨道相比,轨道变宽,向外扩展的程度减小。(u3,u4)参数平面内,受摄共振轨道向外扩展的最大值减小,因此,J2项摄动使得共振轨道的轨道形状发生改变。

图3到和图4分别为仿真时间为50rad和400rad时,受摄共振轨道在参数平面内各个分量方向上的偏差。当选择偏心率为0.8时,从仿真结果可以看出,初始阶段,整体偏差随时间积累,但偏差曲线不光滑,变化并不十分规律。从大约25rad开始,偏差开始保持在某一稳定状态,甚至有略微的减少。到大约180rad时,偏差开始增长,增幅稳定。

图5、图6为采用陈诗瑜推导所得的传统模型,在同等条件下,得到的受摄共振轨道在参数平面内各个分量方向上的偏差。

图1　　　　(u1,u3)平面下理想共振　　　　　图2　　　　(u3,u4)平面下理想共振图3　　　　50 rad内参数平面各分量　　　轨道与受摄共振轨道　　　轨道与受摄共振轨道　　　方向上的整体偏差

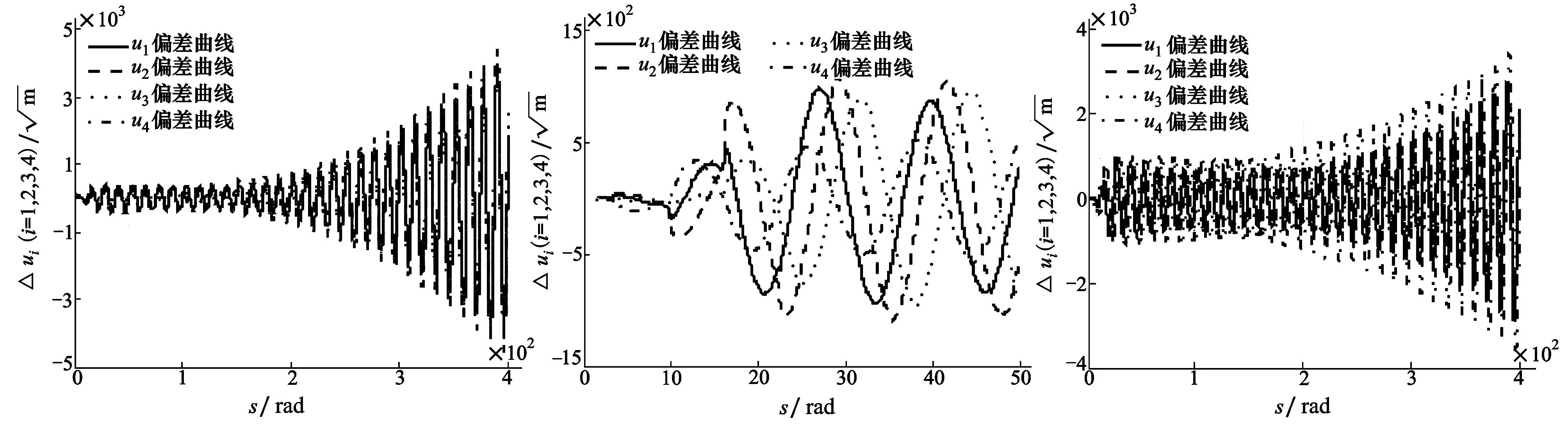
图4　　　　400 rad内参数平面各分量　　　图5　　　　50 rad内参数平面内各个分量图6　　　　400 rad内参数平面内各个　　　方向上的整体偏差　　　方向上的偏差　　　分量方向上的偏差

由此可见,采用本文所建模型得到的仿真结果,与传统模型的仿真结果不同。其原因是由于J2项摄动对系统频率产生干扰,使系统频率无法保持在0.5不变,而参数平面中的推力加速度分量仍选择0.5为频率以期达到共振的效果。这样一来,推力的频率与系统表现出的频率不相等,实际上并未产生共振,因此也无法依靠共振实现小输入产生大的轨道变化以实现节省能源的效果。同时,时间越长,二者差距越大,因此偏差也越来越大。

为进一步深入分析J2项摄动对固有频率的影响,选(16)式为数学模型,取表1、表2中的初始参数进行仿真,结果如图7和图8所示。

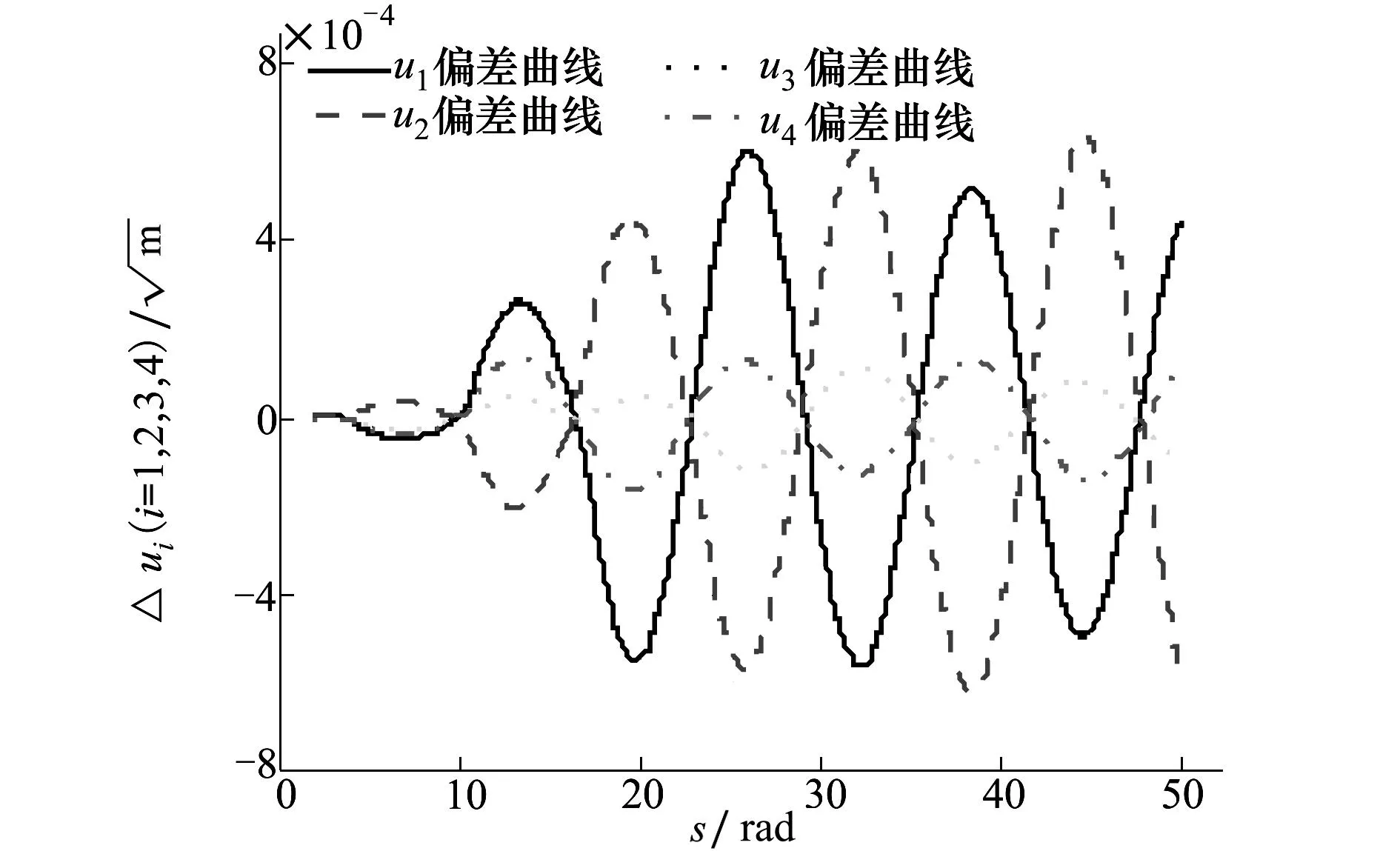
图7　50 rad内参数平面内的局部偏差曲线

图8　400 rad内参数平面内的局部偏差曲线

由图4、图6可以看出,大约前200rad,图4的偏差峰值明显小于图6。其原因是由于在该阶段,J2项摄动对推力的干扰所产生的偏差占主要地位,从(15)式可以看出,J2项摄动并不是将所有力都用来干扰推力,故与(4)式的模型相比,产生的偏差峰值较小。可是从200rad开始,摄动力对固有频率的影响开始变得越来越显著,直接导致整体偏差明显增大,因此400rad结束时,图4的偏差峰值大于图6。由此可以进一步看出,(15)式的数学模型更精确地揭示了J2项摄动使系统产生偏差的原因。

综合上述分析可以看出,考虑J2项摄动中的参数r进行推导所得的数学模型(15)式更准确。另一方面,J2项摄动对共振轨道的影响非常显著,需要施加适当的控制消除或者削弱其对轨道特性的影响。

4结论

本文通过推导,得到了一种新的受J2摄动影响的共振轨道数学模型,并在此基础上进行仿真分析,研究了J2项摄动因素对共振轨道特性的影响。通过与传统受J2项摄动影响的共振轨道数学模型进行对比分析,确定了本文所建数学模型的价值。通过研究表明:

1)在大偏心率情况下,受摄共振轨道相对于理想共振轨道的偏差十分明显。初始阶段,整体偏差随时间积累,偏差曲线不光滑,变换并不十分规律。从大约25rad开始,偏差开始保持在某一稳定状态,甚至有略微的减少。从大约180rad时候,偏差开始增长,增幅稳定。偏差在仿真时间内没有收敛的趋势,增幅随着时间增长越来越大。

2)2种受摄共振轨道模型的仿真结果变化趋势相同,但由于偏差的影响因素有差别,因而偏差的具体变化程度不同。(15)式表示的数学模型虽然形式较为复杂,无法得到解析解,但所得结果能够解释不同阶段J2项摄动使系统产生偏差的原因,因此更为精确。而(4)式所得结果仅趋势正确,虽然形式简洁一些,但准确度较低。若是对短时间的共振轨道进行粗略估计,可以选择(4)式,但是若要精确求解,则建议采用(15)式。

3)J2项摄动对共振轨道的影响非常显著,需要施加适当的控制消除或削弱其对轨道特性的影响。

参考文献：

[1]陈记争. 航天器非开普勒轨道研究[D]. 西安: 西北工业大学, 2010

ChenJizheng.ResearchonNon-KeplerianOrbitsforSpacecrafts[D].Xi′an,NorthwesternPolytechnicalUniversity, 2010 (inChinese)

[2]陈记争, 袁建平, 朱战霞. 航天器共振轨道研究[J]. 宇航学报, 2010, 31(1): 82-86

ChenJizheng,YuanJianping,ZhuZhanxia.ResonanceOrbitforSpacecrafts[J].JournalofAstronautic, 2010, 31(1): 82-86 (inChinese)

[3]史格非. 航天器共振轨道机理及设计方法研究[D]. 西安:西北工业大学, 2014

ShiGefei.ResearchonResonanceOrbitsTheoryandDesignforSpacecrafts[D].Xi′an,NorthwesternPolytechnicalUniversity, 2010 (inChinese)

[4]史格非, 方群, 殷毅. 一般形式的共振轨道研究[J]. 力学与实践, 2014, 36(5):1-6

ShiGefei,FangQun,YinYi.GeneralFormResonanceOrbits[J].MechanicsinEngineering, 2014, 36(5):1-6 (inChinese)

[5]史格非, 方群. 航天器共振轨道特性研究[J]. 飞行力学, 2014, 32(4):334-337

ShiGefei,FangQun.AnalyzeandSimulationontheCharacteristicsofSpacecraftResonanceOrbit[J].FlightDynamics, 2014, 32(4): 334-337 (inChinese)

[6]FangQun,ShiGefei,YinYi.Spacecraft′sResonanceOrbitDesignandApplicationAnalysis[C]∥65thInternationalAstronauticalCongress,Toronto,Canada, 2014

[7]ChenShiyu,LinLin,FangQun.StudyonResonanceOrbitConsideringAirDrag[C]∥14thInternationalSpaceConferenceofPacific-BasinSocieties,Xi′an,China, 2014

[8]DanielCondurache,VladimirMartinusi.ACompleteClosedFormVectorialSolutiontotheKeplerProblem[J].Meccanica, 2007, 42: 465-476

[9]MariaDinaVivarelli.TheKS-TransformationRevisited[J].Meccanica, 1994, 29:15-26

[10]NemesF,Mik′ocziB.PerturbedKeplerProbleminGeneralRelativitywithQuaternions[J].InternationalJournalofModernPhysicsD, 2013, 22(8): 1-22

[11]LegE,GuzzoM,Froeschl′eC.DetectionofCloseEncountersandResonancesinThree-BodyProblemsthroughLevi-CivitaRegularization[J].MonNotRAstronSoc, 2011, 418: 107-113

[12]PrasenjitS.InterpretingtheKustaanheimo-StiefelTransforminGravtionalDynamics[J].MonNotRAstronSoc, 2009, 400: 228-231

[13]KatsuhikoYamada,TakeyaShima,ShojiYoshikawa.EffectofJ2PerturbationsonRelativeSpacecraftPositioninNear-CircularOrbits[J].JournalofGuidance,Control,andDynamics, 2010, 33(2): 584-590

[14] 马庆甜. 连续小推力卫星的几种典型非开普勒轨道设计[D]. 北京：清华大学, 2011

MaQingtian.DesignofSeveralTypicalNon-KeplerianOrbitsforSatellitewithContinuousLow-thrust[D].Beijing,TsinghuaUniversity, 2011 (inChinese)

[15] 李俊峰, 孟鑫, 高云峰, 李响. J2摄动对编队飞行卫星相对轨道构形的影响[J]. 清华大学学报:自然科学版, 2004, 44(2): 224-251

LiJunfeng,MengXin,GaoYunfeng,LiXiang. J2PerturbationEffectonRelativeOrbitalConfigurationofSatellitesinFormationFlying[J].JTsinghuaUniv(Sci&Tech,) 2004, 44(2): 224-251 (inChinese)

Studying Spacial Resonance Orbit withJ2Perturbation Considered

Lin Lin1,2, Fang Qun1,2

(1．College of Astronautics，Northwestern Polytechnical University，Xi'an 710072，China 2．National Laboratory of Aerospace Flight Dynamics，Xi'an 710072，China)

Abstract:The spacial resonance orbit is a non-Keplerian orbit created in a new coordinate system. It can be applied to the design of the spacial maneuvering orbit and has the advantage of saving fuel. For the spacial resonance orbit affected by J2 perturbation, a new perturbed model, applied to random inherent frequency, is developed in this paper. And then, the J2 perturbation effect on the resonance orbit characteristic is analyzed with simulation. Compared with thesimulation of the traditional perturbed model, it shows that although the new perturbed model has a more complex form, it can explain the source of differences in different stages. So it is more accurate and can analyze the J2 perturbation effect on the resonance orbit characteristic, better.

Keywords:acceleration, computer simulation, design, diffential equations, fuels, functions, maneuverability, mathematical models, mathematical transformations, matrix algebra, natural frequencies, orbits polynomicals, resonance, spacecraft, vectors, vibrations(mechanical); J2 perturbation, non-Keplerian, resonance orbit

中图分类号：V212.1

文献标志码：A

文章编号:1000-2758(2016)01-0147-06

作者简介：吝琳(1990—),女，西北工业大学硕士研究生,主要从事飞行力学与控制的研究。

基金项目：国家自然科学基金(11272255)资助

收稿日期：2015-03-17