基于LMS算法的窄带干扰检测技术

张兆林, 李路, 姚如贵, 王伶

(西北工业大学 电子信息学院, 陕西 西安　710072)



基于LMS算法的窄带干扰检测技术

张兆林, 李路, 姚如贵, 王伶

(西北工业大学 电子信息学院, 陕西 西安710072)

摘要：直扩系统通常采用干扰抑制技术提高系统的干扰容限。在无干扰或小干扰情况下，直接进行干扰抑制会给接收端带来极大的信噪比损失，而窄带干扰检测技术可以有效解决这一问题。传统的窄带干扰检测技术常用于低信噪比情况下，而本文提出的基于LMS算法的干扰检测算法能够较好的适用于大信噪比范围与高信噪比情况，对于不同的信噪比该算法可以自适应选取相应的门限以较高的干扰检测率与较低误检率有效检测干扰，同时相对于其他算法该算法原理简单，容易实现。

关键词：直扩系统； LMS算法；信噪比；干扰检测；误检率

直接序列扩频通信体制由于具备良好的抗干扰、抗截获及保密通信能力，是目前国内外各类数据链中应用最广泛、最成熟的通信体制之一[1]。然而，面对更高的抗干扰要求时，受限于目前器件的处理能力和信道带宽，仅依靠增大扩频处理增益来提高直扩系统自身的抗干扰容限是不现实的。因此，需要对接收信号进行干扰抑制处理，以进一步增强系统的干扰抑制能力。然而在无干扰或小干扰情况下，直接进行干扰抑制会给接收端带来极大的信噪比损失，而窄带干扰检测技术可以有效解决这一问题。

传统的干扰检测及抑制算法大都工作在地面接收，低信噪比条件下，而在采用扩频技术的星间通信中，由于收发双方的距离远近差别大，扩频信号功率具有大动态范围，导致星间通信信噪比动态范围较大。在高信噪比条件下，当不存在干扰或干扰很小时，传统的干扰检测算法不再适用，因此，需要寻求一种有效的干扰检测技术以适用于高信噪比情况与大信噪比范围的条件，使信号在无干扰或小干扰情况下不经干扰抑制而直接通过，在强干扰下进行干扰抑制处理，以提高系统性能。

目前窄带干扰检测技术主要分为时域检测技术和频域检测技术2类，时域检测技术以误差预滤波技术为主[2]；频域检测技术以FFT算法的陷波干扰抑制技术为主[3]。文献[4]根据接收信号频谱的统计特性，实时估计信道白噪声和干扰之间的门限，给出一种基于自适应门限的窄带干扰抑制算法，可在有效判决出干扰信号后进行抑制处理。文献[5]提出了一种基于傅里叶变换的双门限干扰检测算法(localization algorithm based on double-threshold,LAD)，通过迭代计算高低门限，将变换域幅值分别与2个门限比较进行干扰检测。文献[4]提出的自适应门限算法以及文献[5]提出的双门限算法均适用于低信噪比情况，当信噪比范围大或是高信噪比时这2个文献所提算法会失效。然而本文提出的基于LMS算法的干扰检测算法针对不同信噪比自适应选取相应的门限值，能在高信噪比情况与较大的信噪比动态范围内对接收信号以较小的误检率，较大的干扰检测率进行有效干扰检测。

1LMS算法原理

最小均方(LMS)算法是时域干扰抑制算法中应用最为广泛的一种，它原理简单，容易实现，主要利用窄带干扰与扩频信号在预测性上的差异来抑制干

扰[6]。本节介绍了LMS算法的基本原理，重点研究了归一化LMS算法，从算法的收敛速度与稳态误差2个方面分析了归一化LMS算法的性能。

1.1LMS算法

Widrow和Hoff于1960年提出以瞬时误差信号平方的梯度作为均方误差函数梯度的估计，得到最小均方(LMS)算法，LMS算法作为一种线性自适应滤波算法，其实现结构简单，是一种使用广泛的自适应算法[7]。

预测滤波器的输入信号矢量x(n)=[x(n-1),x(n-2),…,x(n-L)],y(n)为滤波器的输出,可得

(1)

式中,ω(n)为滤波器的权矢量。设期望响应为d(n),那么线性预测滤波器的误差信号为

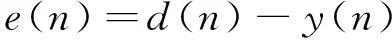
(2)

由于最小均方误差是由瞬时误差信号平方的梯度作为均方误差函数梯度的估计,可得

(3)

易得到

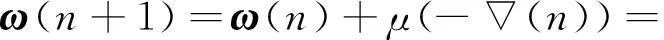
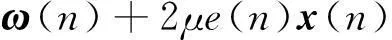
(4)

式中,μ为滤波器迭代步长。(4)式即是LMS算法权向量的迭代公式。从公式中可以看出,LMS算法的原理非常简单,它既不需要计算有关的相关函数,也不需要矩阵求逆运算。

在LMS算法收敛的范围内,迭代步长μ越大,算法的收敛速度越快,但LMS算法的失调也越大,算法性能也越不稳定,因此LMS算法的收敛速度与失调之间存在着矛盾[8]。在保证滤波器一定的失调性能的情况下,如何缩短收敛过程成为一个值得研究的问题。针对这个问题,变步长LMS算法应运而生。下面,详细介绍一种现有的变步长LMS算法——归一化LMS算法[9]。

1.2归一化LMS算法

定义滤波器的更新权向量ω(n+1),要使权向量的增量δω(n+1)满足

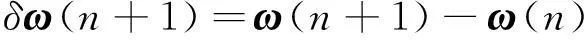
(5)

欧几里德范数最小化,而且要满足

(6)

使用拉格朗日乘子法,可得归一化LMS算法的代价函数为

(7)

式中,λ表示拉格朗日乘子。将代价函数J(n)对ω(n+1)求导置零,即可得到更新权向量。将(7)式对ω(n+1)求导如下

(8)

令上式等于零,可得最优更新权向量为

(9)

将其带入公式(6),化简可得:

(10)

式中，e(n)表示估计误差。将λ带入(9)式并引入常量μ,更新权向量可表示为

(11)

称(11)式为归一化LMS算法抽头权向量的迭代公式。(11)式等号右边第2项为算法权向量的修正项,该修正项经抽头输入向量欧几里德范数的平方归一化。

同公式(4)的权向量迭代公式比较,可以看出,若设

(12)

那么,归一化LMS算法实际上就是一种变步长的LMS算法。由于归一化LMS算法是在LMS算法随机梯度估计的基础上对抽头输入向量的欧几里德范数平方进行了归一化。因此,无论是对于相关数据还是非相关数据,归一化LMS算法提高了LMS滤波算法的收敛速度,克服了自适应滤波收敛速度与稳态噪声之间的矛盾[10],其抗干扰性能优于传统LMS算法。

2干扰检测算法

信噪比动态范围大特别是高信噪比条件下,当无干扰或干扰小时直接进行抑制处理会带来较大的信噪比损失。因此,有必要对接收信号进行干扰检测,以便判定是否对接收信号进行干扰抑制处理。

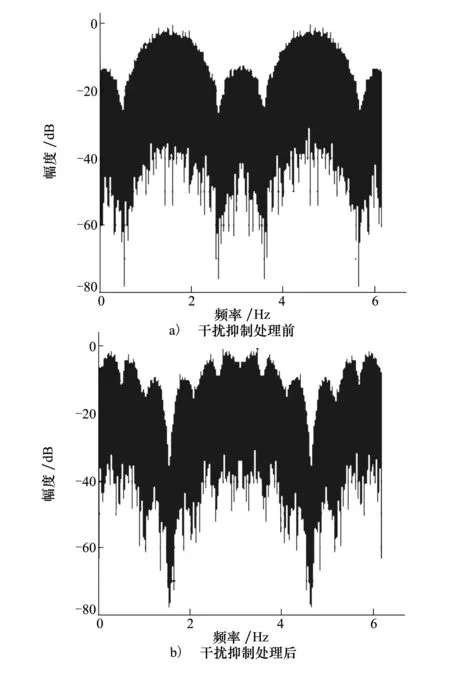
图1　无干扰进行干扰抑制处理前后信号频谱

为了验证无干扰时干扰抑制对信号带来的能量损失,我们设置仿真参数为:采样频率62MHz,伪码速率10.23MHz,中频15.48MHz,信噪比为10dB。图1给出了不存在干扰时采用归一化LMS算法对接收信号进行干扰抑制处理前后信号频谱的对比。从图中可以看出由于干扰抑制使信号产生损伤,输出信号的波形严重失真,进一步降低了输出信噪比。

针对归一化LMS算法在无干扰或小干扰情况下对信号损伤巨大的问题,本文在归一化LMS算法基础上,提出了基于LMS的干扰检测算法。通过将自适应滤波模块的输出信号与输入信号功率的比值取对数后与设定的门限进行比较,以判断接收信号有无干扰。该干扰检测算法原理简单、容易实现、复杂度低。数据的处理流程如图2所示。

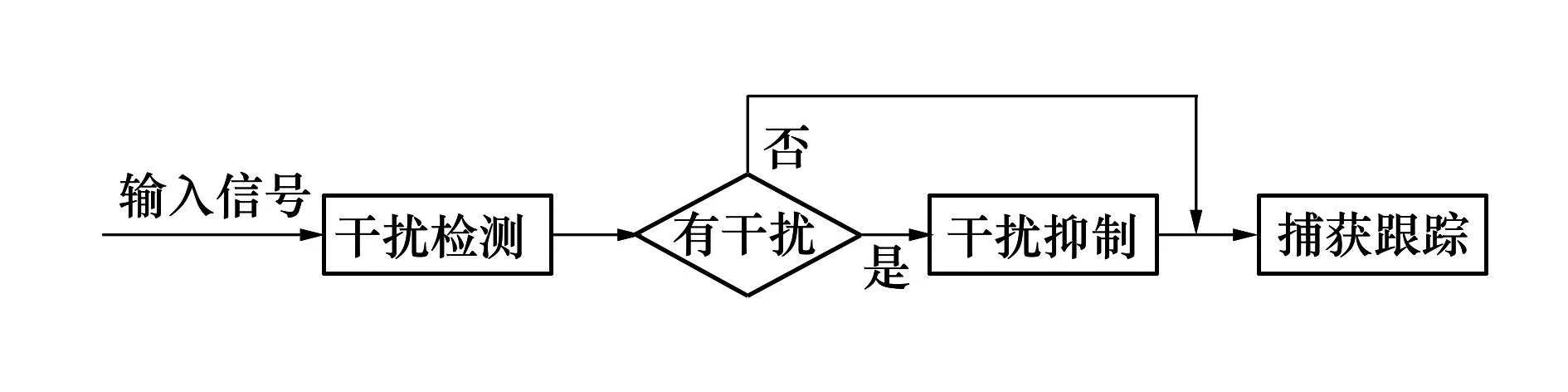
图2　数据处理流程

由文献[11]可知,在迭代步长较小时,LMS算法对无干扰和小干扰信号滤除较浅,对强干扰信号不能完全滤除;在迭代步长较大时,LMS算法对强干扰信号抑制较好,但会使无干扰和小干扰信号失真严重。本文提出的基于LMS的干扰检测算法正是基于以上特性,通过比较小步长LMS滤波器的输出信号与输入信号功率比值的对数与设置的合理门限值的大小来判断有无干扰。

2.1基于LMS的干扰检测算法原理

图3为基于LMS的干扰检测与抑制算法原理框图:

图3　基于LMS的干扰检测算法原理框图

图3中所采用的判决滤波器与干扰抑制模块均采用归一化LMS算法抑制干扰,其中为输入信号,为输出信号。调节(12)式中的参数可改变迭代步长的大小。下面对该算法进行具体描述:

1) 将输入的数据分路成为2路,第1路数据送入采用小步长LMS算法的判决滤波器进行干扰检测,第2路数据送入延时模块。

2) 判决滤波器对输入信号进行LMS迭代滤波,并计算滤波器输出信号和输入信号的功率比值并取对数记为Mn。

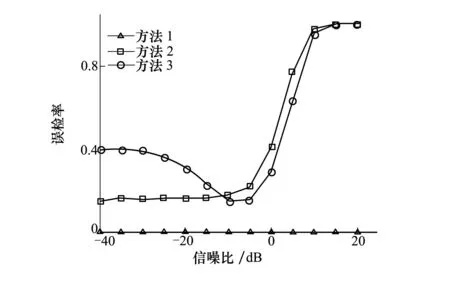
3) 在判决模块中对比Mn与设定的门限TH来判断干扰有无并输出对应的控制信号。当Mn>TH时,表明无干扰或干扰很小,当Mn

4) 干扰判决模块输出的控制信号控制选通开关。若无干扰或干扰较小,则选通开关将第2路数据输给直通模块;若存在较强干扰,则选通开关将第2路数据输给采用大步长LMS算法的干扰抑制模块进行干扰抑制处理。

如图3所示,本文所提基于LMS算法的干扰检测算法原理简单、容易实现,只需要在归一化LMS算法的基础上增加一个采用小步长LMS算法的判决滤波器与一个直通模块,系统的复杂度较低。该算法适用于较大的信噪比动态范围,尤其是在高信噪比下,也能有效检测干扰的有无,这是该算法相对于其他算法最大的优势。该干扰检测算法的门限设置最为关键,下面给出门限选取的方法。

2.2门限的选取

门限的选取是本文所提干扰检测算法的关键,下面具体论述如何选取合理的门限值。

我们定义

(13)

为输出信号与输入信号的功率比值,其中Pout(x)为信号经干扰抑制处理后的功率,Pin(x)为干扰抑制模块输入端信号功率。

我们设定干信比小于20 dB的干扰信号为小干扰,其能通过直扩系统本身的干扰容限被抑制;而干信比大于20 dB的干扰为大干扰,需要经过干扰抑制模块进行干扰抑制处理。因此,可设定干信比为20 dB时的输出信号与输入信号功率比值Mn为门限值,即

(14)

(14)式则为本算法选取门限的依据,其中TH为门限值。

表1是由MATLAB仿真数据通过统计得出的TH在不同信噪比下较好的门限取值范围，其中，仿真参数设置为：采样频率65 MHz，伪码速率10.23 MHz，中频16.84 MHz，(12)式迭代步长中参数μ=3。TH的取值与干扰的大小无关，仅与接收信号的信噪比有关。

表1　取值范围

3仿真结果与分析

本节通过MATLAB仿真验证所提算法的性能。仿真参数设计如下：数据流速率为500 bits/s，伪随机序列速率为10.23 MHz，扩频后采用BPSK调制，接收端的中频为16.84 MHz，采样频率为65 MHz，窄带干扰带宽为2 MHz。

误检率和干扰检测率常用于衡量干扰检测算法性能。误检率是指算法在无干扰或小于所需检测干扰强度时判断为有干扰的概率。干扰检测率是指在干扰大于所需检测干扰强度时正确检测出干扰的概率。考虑到信号的信噪比动态范围大，如果：①一个算法的误检率很低；②在低信噪比强干扰下的干扰检测率很高，小干扰下的干扰检测率很低；③在高信噪比强干扰的检测率大，对小干扰的检测率小，则认为该算法的性能好。在这里干扰信号的强弱是相对噪声而言的。

为了验证本文所提算法的性能改善，我们对比以下几种方法：记方法1为本文所提基于LMS的干扰检测算法。根据文献[4]提出的自适应门限选择的理论依据，可记方法2为DFT+自适应的门限检测算法。记文献[5]提出的LAD算法为方法3。方法2用到了自适应的门限算法，这里门限的选取是文献[4]提出的自适应门限选择理论。对比3种方法的误检率和干扰检测率，可以评估3种算法在高信噪比情况与较大的信噪比范围内的性能。

仿真中方法1根据表1，在不同的信噪比范围内设置相应的门限值，方法2的自适应门限系数k=8，考虑到工程应用，方法3的高低门限系数分别为2和4，试验次数10 000次。

3.1无干扰情况

图4分别给出了在无干扰条件下3种检测算法的误检率曲线。

图4　无干扰条件下3种方法的误检率曲线

对比3种方法的误检率曲线可以看出：(1)方法1在整个信噪比区间的误检率最低，小于0.1%；(2)方法2在整个信噪比区间的误检率随信噪比的增加呈上升趋势，低信噪比区间误检率在15%上下，呈上升趋势，低信噪比区间误检率在15%上下，高信噪比区间误检率急剧增大，高达70%以上；(3)方法3在整个信噪比区间的误检率随信噪比的增加呈下降-上升的趋势，在整个区间内的误检率都偏大。分析原因可知：扩频信号和噪声之和在高信噪比条件下不再近似服从高斯分布，门限系数的设置已经失效，因此在高信噪比下方法2和方法3的误检率很大，且误检率随着信噪比的提高而增大。方法1根据不同的信噪比设置了相应的门限，并不只针对高斯分布，对高信噪比下的其他分布同样适用。

3.2有干扰情况

本节将对比方法1～3在高低信噪比下的不同干扰类型的检测性能，这里将以10 dB和-20 dB分别代表高低2种信噪比。

图5和图6分别给出了3种检测算法针对不同强度点频和窄带干扰的检测率。

由仿真结果可以看出：点频干扰和窄带干扰的检测结果相近，只是相同条件下同强度的点频干扰的检测率大于或等于窄带干扰的检测率。这是因为相同强度的点频干扰相对窄带干扰能量更集中，因此也更容易检测。对比图5和图6中的检测曲线可以看出：(1)方法1～3对低信干比下的干扰检测性能十分接近，3种方法基本可完全检测干扰；(2) 方法2在高低信噪比下对小干扰检测率达分别达90%和15%以上； (3)方法3在高低信噪比下对小干扰检测率达分别达90%和15%以上；(4) 方法1在高低信噪比下对小干扰的检测率都很低，特别是在高信噪比下，方法1的小干扰检测率远小于方法2和方法3。

方法2和方法3在高低信噪比下对小干扰的检测率都较方法1大，尤其是在高信噪比条件下。从误检率来讲方法1的误检最小，性能最优；从干扰检测率来讲，方法1对强干扰的检测性能与方法2和方法3相近甚至更好一些，且方法1对小干扰的检测性能更是优于方法2和方法3。因此综合误检率和干扰检测率，方法1的性能最优。

4结论

本文提出基于归一化LMS算法的干扰检测算法，通过比较小步长LMS滤波器的输出信号与输入信号功率的比值与设置的合理门限值的大小来判断有无干扰，原理简单、容易实现且复杂度低。本文所提干扰检测算法避免了高信噪比条件下信号的误检问题，并降低了对小干扰的检测概率，尤其是在高信噪比条件下，适用于信噪比变化较大的星间通信。

参考文献：

[1]李婷婷, 张春泽, 王书省. 变换域窄带干扰检测算法研究[J]. 现代电子技术, 2014, 37(17): 32-35

Li Tingting, Zhang Chunze, Wang Shusheng. Research of Narrowband Interference Detection Algorithm in Transform Domain[J]. Modern Electronic Technology, 2014, 37(17): 32-35 (in Chinese)

[2]Batra A, Zeidler J R. Narrowband Interference Mitigation in OFDM Systems[C]∥Military Communications Conference, IEEE, 2008: 1-7

[3]毕晓君, 邵然. 自适应匹配追踪的OFDM系统窄带干扰检测[J]. 哈尔滨工程大学学报, 2014, 35(7): 908-912

Bi Xiaojin, Shao Ran. Narrowband Interference Detection for OFDM Systems of the Sparsity Adaptive Matching Pursuit[J]. Journal of Harbin Engineering University, 2014, 35(7): 908-912 (in Chinese)

[4]张爱民, 胡艳龙, 韩方景. 低信噪比下基于自适应门限的窄带干扰抑制研究[J]. 电子信息对抗技术, 2009, 24(1): 51-54

Zhang Aimin, Hu Yanlong, Han Fangjing. Research on Narrowband Interference Suppression Based on Adaptive Threshold under Low SNR[J]. Electronic Information Warfare Technology, 2009, 24(1): 51-54 (in Chinese)

[5]Vartiainen J, Lehtomaki J J, Saarnisaari H. Double-Threshold Based Narrowband Signal Extraction[C]∥Proceedings of 61st IEEE Vehicle Technology Conference(VTC), Stockholm, Sweden, 2005: 2394-2398

[6]王宏. 直扩系统中窄带干扰抑制技术的研究[D]. 哈尔滨：哈尔滨工程大学, 2012

Wang Hong. The Research of Direct Spread System Narrow Band Interference Suppression Technology[D]. Harbin, Harbin Engineering University,2012 (in Chinese)

[7]郝东方. 卫星通信干扰技术的研究[D]. 西安：西安电子科技大学, 2012

Hao Dongfang. Research on The Jamming Technology of Satellitte Communication[D]. Xi′an, Xi′an University of Electronic Science and Technology,2012 (in Chinese)

[8]曹亚丽. 自适应滤波器中LMS算法的应用[J]. 仪器仪表学报, 2008 (增2): 452-454

Cao Yali. The Application of LMS Algorithm in Adaptive Filter[J]. Journal of Instrument and Meter, 2008(Suppl 2): 452-454 (in Chinese)

[9]曾照福, 赵巧红. 归一化LMS算法自适应滤波器的MATLAB仿真与DSP实现[J]. 湖南科技大学学报:自然科学版, 2010(3): 017

Zeng Zhaofu, Zhao Qiaohong. MATLAB Simulation and DSP Realization of Normalized LMS Adaptive Filter[J]. Journal of Hunan University of Science and Technology: Edition of Natural Science, 2010(3): 017 (in Chinese)

[10] 李竹, 杨培林, 行小帅. 一种改进变步长LMS算法及其在系统辨识中的应用[J]. 仪器仪表学报,2007, 28(7): 1340-1344

Li Zhu, Yang Peilin, Xing Xiaoshuai. Modified Variable Step Size LMS Algorithm and Its Application in System Identification[J]. Journal of Instrument and Meter, 2007, 28(7): 1340-1344 (in Chinese)

[11] 谢皓臣. 基于直扩系统窄带干扰建模及时域干扰抑制设计与仿真[D]. 长沙：国防科学技术大学, 2012

Xie Haochen. Design and Simulation on Narrow-Band Interference Suppression Algorithm in Spread Spectrum Communication System[D]. Changsha, National University of Defense Technology,2012 (in Chinese)

Narrowband Interference Detection Technique Based on Least Mean Square Algorithm

Zhang Zhaolin, Li Lu, Yao Rugui, Wang Ling

(Department of Electronics Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:Interference suppression technique is usually used to improve the interference tolerance of DSSS (Direct Spread Spectrum System). In the case of no interference or little interference, direct implementation of interference suppression will causes a great SNR loss at receiver. Narrowband interference detection technique can effectively solve this problem. Classical narrowband interference detection technique can only work well at low SNRs. In this study, a novel interference detection algorithm based on LMS algorithm is proposed; this algorithm can be adopted at a large range of SNRs or at high SNRs. For different SNRs, this algorithm can adaptively select threshold to detect interference effectively with high detection rate as well as low false detection rate. Compared with other algorithms, the algorithm is simple in principle and easy to implement.

Keywords:DSS(Direct Spread Spectrum System); LMS( Least Mean Square) algorithm, signal to noise ratio, interference detection; false detection rate

中图分类号：TN911.4

文献标志码：A

文章编号:1000-2758(2016)01-0092-06

作者简介：张兆林(1978—)，西北工业大学副教授、博士，主要从事无线通信、卫星导航抗干扰及多媒通信研究。

收稿日期：2015-10-09基金项目：国家自然科学基金(61271416、61301093、61501376)、中央高校基本科研业务费专项基金(3102014KYJD027)与陕西省自然科学基础研究计划(2014JM2-6094)资助