跨声速轴流压气机多叶排反问题优化方法

刘昭威, 吴虎, 唐晓毅

(西北工业大学 动力与能源学院, 陕西 西安　710072)



跨声速轴流压气机多叶排反问题优化方法

刘昭威, 吴虎, 唐晓毅

(西北工业大学 动力与能源学院, 陕西 西安710072)

摘要：为提升跨声速压气机的气动性能,以叶轮机械三维黏性反问题设计理论为基础，发展了适用于压气机多叶排三维反问题优化设计方法。描述了压气机多叶排流场计算所采用的数值求解技术，详细推导了反问题优化设计方法和流程。为验证方法的正确性，运用德国宇航中心单级跨声速压气机R030-SUKS/31的实验数据与计算结果进行对比。在对原型叶片表面载荷进行分析的基础上，重新修改叶片表面载荷分布，并通过反问题设计方法计算得到新的叶片几何构型。结果表明，通过修改叶片表面载荷分布，运用反问题设计方法得到的压气机，其进口相对马赫数有所提升，压气机流量和压比分别提高了3.5%和2.0%，气动性能有明显提升，验证了方法的正确性和有效性。

关键词：反问题设计方法；载荷分布；优化设计；跨声速压气机

随着航空发动机总体性能的提升，风扇以及增压级的设计难度不断增大。为了提高发动机的推重比，降低单位燃油消耗率，风扇和压气机的设计压比不断提高，压气机设计朝着高负荷，高叶尖马赫数的方向发展。当前较为先进的航空发动机风扇和压气机前几级均采用超声速或跨声速设计，其最大的特点就是叶片通道内部存在激波，气体流动的三维效应较强，流动损失的产生原因复杂。因此，跨声速压气机的气动优化设计十分重要。

20世纪80年代初，Denton[1]首次将全三维计算流体力学(computational fluid dynamics,CFD)技术应用于叶轮机械设计领域。经过多年的发展，CFD在叶轮机械设计中的应用已日臻成熟。其主要作用是对叶轮机械内部流场进行数值模拟和性能预测，并以此为依据对叶片几何构型进行优化设计，以期得到较好的气动性能。这种已知叶片几何构型求解气动性能的过程通常被称为正问题求解。在实际设计过程中，为了得到一个气动性能较好的叶片几何构型，往往需要对叶片型面坐标进行不断调整，反复计算，这需要耗费大量的时间和计算资源。因此，设计人员提出了一种全新的设计方法，通过给定叶轮机械的气动性能参数来求解叶片的几何构型，即反问题设计方法。

反问题设计方法从20世纪80年代中期开始起步，近期已经成为国际上研究的热点问题。最初的反问题求解的是二维势流方程，随着正问题求解方法的不断改进，反问题设计也逐步扩展到求解Euler方程和Navier-Stokes方程。Dang[2]采用4阶 Runge-Kutta时间推进、基于网格中心的有限体积法求解二维Euler定常流场，发展了反问题所适用的渗透边界条件，并建立了一套二维反问题设计方法体系。Ghaly等[3]通过给定目标静压，计算虚位移的方法进行叶片几何构型更新，并应用于压气机叶栅的改型设计，取得了良好效果。随着三维CFD技术的逐步成熟，三维反问题设计方法不断发展。Qiu等[4]基于非均匀有理B样条曲线(NURBS)和最小二乘的思想，提出了一种统一的叶片中弧面生成方法，增强了方法的鲁棒性。

国内对反问题设计方法的研究起步并不晚，西北工业大学周新海等[5]基于有限体积法求解Euler方程进行了跨声速叶栅的反问题求解方法研究。北京理工大学杨策等[6]采用规定叶片表面无量纲目标速度分布，通过比较目标速度分布和计算获得的速度分布来修改叶片压力面和吸力面的坐标，最终

获得满足要求的叶片形状。中科院工程热物理所的王正明等[7-8]从1985年就开始研究二维反问题，并在2000年发展了黏性的三维反问题设计方法，该方法基于非正交曲线坐标系下完全守恒型Navier-Stokes方程和B-L湍流模型，运用MacCormark显式时间推进，并运用该方法进行叶型设计。杨金广[9]采用有限体积法求解三维Navier-Stokes方程，并基于渗透边界条件以及叶片表面载荷分布来改变叶片形状，建立了三维黏性叶轮机械反问题设计体系。

目前的叶轮机械反问题设计主要针对平面叶栅和单叶排叶片几何构型，将反问题应用于多叶排乃至多级叶轮机械设计的研究较少。国外方面，van Rooij等[10]利用反问题设计方法研究多级压气机多叶片排优化改型设计，取得了良好效果。国内对于叶轮机械多叶排反问题的研究较为欠缺，从公开发表的文献来看，尚未有较为显著的研究成果。

本文在课题组前期的研究基础上，采用反问题设计方法，对单级双叶片排跨声速压气机进行反问题改型设计研究。文中介绍所使用的反问题设计方法的计算模型，以德国宇航中心(Deutsches Zentrum für Luft-und Raumfahrt,DLR)单级跨声速压气机R030-SUKS/31的实验数据为依据验证求解器的正确性，并运用叶片返回实验验证反问题求解的精度和有效性。最后针对该跨声速压气机流场特点对叶片表面载荷分布进行优化改进，运用反问题设计方法求出新的叶片几何构型，从而优化叶片通道中的流动结构和激波强度，并通过对比流场及转子出口气动性能参数，验证方法的有效性。

1模型和计算方法

1.1控制方程及数值求解方法

反问题设计方法所求解的控制方程与正问题相同，本文中采用求解积分形式的Navier-Stokes方程，其具体形式如下：

(1)

式中,Ω为控制体体积，∂Ω为控制体边界，n为控制体边界外法向量，W为通量变量，Fl为对流通量，Fv为黏性通量。本文采用基于网格中心点的有限体积法对控制方程进行离散求解，运用Jameson所发展的改进JST格式进行通量求解，时间推进采用5步混合Runge-Kutta法，CFL数达到3.6，湍流模型采用S-A模型，为了保证求解的稳定性，只采用了当地时间步长一项加速收敛措施。

在叶轮机械多叶排流场数值模拟中，动、静叶片排之间的掺混面(mixing-plane)的处理较为重要，掺混面不仅需要正确传递上、下游叶排流场信息，还必须尽量消除特征波反射对数值求解的影响。Giles[11]基于线性Euler方程提出了一整套无反射边界条件理论，Chima[12]将该套理论应用于叶轮机械多叶排掺混面的处理，取得了良好效果。本文所采用的掺混面数值计算方法均基于上述理论。作者在前期工作中基于上述理论，自主开发了一套压气机全三维黏性流场数值计算程序[13]，能够较为准确地预测跨声速轴流压气机的气动性能，本文的工作均是该套计算程序的基础上开展的。

1.2反问题计算方法

反问题设计方法的本质是通过给定叶片周围流场的气动参数分布从而得到叶型几何数据，气动参数的分布由设计者给定。本文中所给定的气动参数为叶片表面沿轴向的载荷分布，即叶片吸力面与压力面之间的压力差 ，Dang[2]对叶片载荷与叶片对气流的加功量之间关系进行了详细推导。反问题计算的核心是反问题边界条件。本文所采用反问题边界条件基于无滑移物面边界条件，保证叶片几何构型更新前后叶片表面的特征值守恒。通过所给定的叶片表面载荷 与迭代计算过程中的载荷之差，求解壁面的虚拟移动速度 。

(2)

式中正、负号分别代表叶片的上、下表面，ρ和c分别为邻近壁面处的气体密度和声速。令叶片中弧面的虚拟法向速度Wn与叶片上下表面相等

(3)

用虚拟速度乘以相应的时间步长，则可以求出叶片中弧面的虚拟位移δf

(4)

由于时间步长与实际流场中的参数变化相关，因此选取时间步长Δt为邻近壁面的当地时间步长，nθ为叶片中弧面法向量的切向分量，计算过程中，保证叶片的轴向和径向坐标不改变，只改变切向坐标，则更新后的叶片中弧面坐标可表示为

(5)

计算时周期性的更新中弧面，选取中弧面上某一条径向网格线作为积叠线，保持其切向坐标不变，更新中弧面时从该条积叠线开始，顺流动方向或者逆流动方向分别求解更新后的中弧面坐标。

保持原始叶片厚度不变，将其叠加至更新后的中弧面，最终求出更新后的叶片吸、压力面坐标。运用更新后的叶片几何构型重新进行网格划分，继续进行计算，直至流场收敛。改进后的反问题求解流程如图1所示。

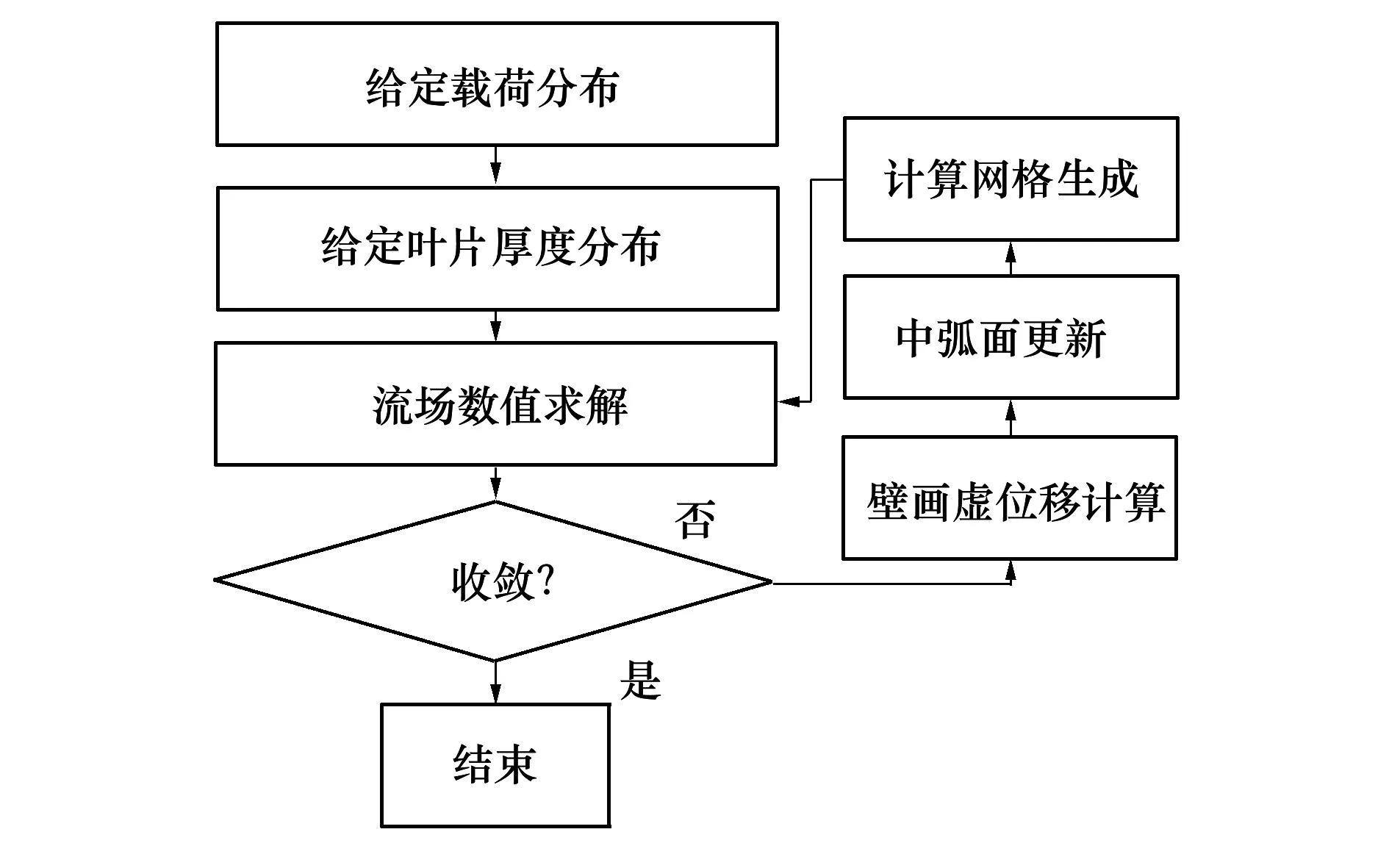
图1　反问题设计计算流程

2计算结果及分析

2.1正问题求解验证

为了保证反问题计算的正确性，首先需对正问题求解器进行验证。本文首先应用所发展的正问题计算程序对德国宇航中心单级跨声速压气机R030-SUKS/31近峰值效率工况点进行气动计算，并将计算结果与实验数据[14]进行对比，表1为该压气机的实验工况。

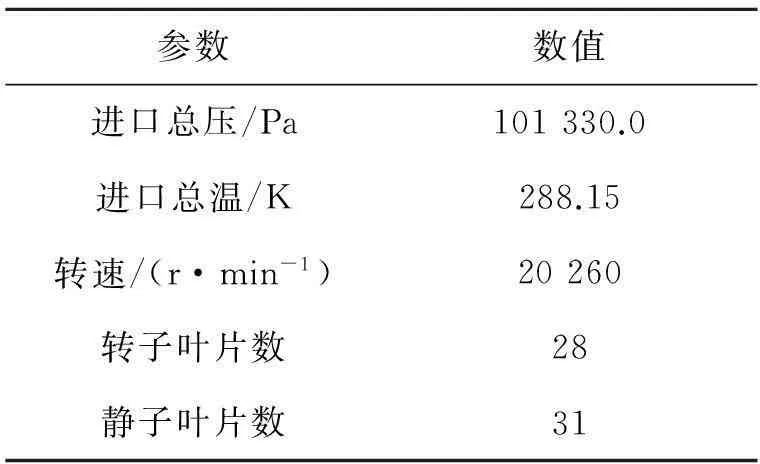
表1　R030-SUKS/31跨声速压气机级实验工况

计算给定的收敛标准为连续方程通量变量残差收敛至 ，进、出口流量偏差小于0.5%。表2为R030-SUKS/31单级压气机峰值效率点附近气动参数计算值和实验值的对比，可见计算结果与实验值符合较好，计算精度能够满足工程实用要求。

表2　　　　R030-SUKS/31跨声速压气机级气动性能

2.2叶片返回实验

为了验证反问题求解的正确性，本文进行了反问题叶片返回实验。将原始叶片的载荷分布作为目标载荷，以保证反问题解的存在性，在保证叶片厚度分布不变的基础上通过人为改变中弧面生成新的叶片，将新叶片作为初始几何，运用反问题计算使之稳定收敛到原始叶片几何构型，证明收敛解的唯一性以及反问题求解方法的可靠性。反问题计算的收敛标准以及进、出口边界条件与正问题求解相同。求解初始阶段给定前文中正问题计算所得到的叶片表面载荷分布，叶片的厚度分布以及一个初始的中弧面坐标。

图2为反问题计算最终收敛后3个不同展向位置叶片截面型线之间的对比，左侧为转子，右侧为静子。由图中可以看出，在不同的展向位置，叶片截面型线均与原始叶型符合较好，可见反问题计算的结果与原始叶型几何符合较好。同时，反问题计算结果很好的满足了给定的叶片表面载荷分布。叶片返回实验验证了反问题计算程序的精度和可靠性。

图2　叶片返回计算结果与原始叶型对比

2.3多叶排反问题改型优化设计

反问题设计方法的最大优势在于其直观性，设计人员可以根据设计意图，给定气动参数分布，求得满足气动参数分布的叶片几何构型。本文采用反问题设计方法，对德国宇航中心单级跨声速压气机R030-SUKS/31峰值效率点附近的叶片表面载荷进行优化改型设计，力求提升该跨声速压气机气动性能。

跨声速压气机转子叶片弯角较小，与亚声速压气机的增压原理不同，跨声速压气机转子主要依靠叶片通道内的激波进行增压，且波前马赫数越大，激波强度越高，增压能力越强，但过高的激波强度会造成较大的激波损失。而激波在叶片通道内的位置与强度能够较为直观的体现在叶片表面的载荷分布上。

图3为R030-SUKS/31单级跨声速压气机转子、静子叶片载荷分布等值线图。图中等值线分布的疏密程度代表了载荷梯度的大小。从图中的叶片表面载荷分布可以看出，转子的叶片载荷从叶根到叶尖逐渐增大，在50%叶高以上的部分，载荷沿流动方向先增大后减小，叶片通道内激波与吸力面和压力面相交的位置与载荷变化较为剧烈的位置相对应。而静子叶片载荷沿径向的分布变化不大，该压气机静子叶片采用可控扩散叶型，载荷主要分布在叶片前半部分。

图3　原始叶片表面载荷分布等值线图

由于该单级压气机峰值效率已经达到90%，该工况点效率的提升空间有限，因此对其优化改型的主要目标是在保持效率基本不变，增大该工况下的流量和压比。在对转子叶片载荷进行调整时，首先保证叶片通道内激波与叶片的相对位置不发生明显变化，在此基础上适当增加来流相对马赫数，一方面增加了激波强度和压比，另一方面也增大了流量。为达到上述目的，转子叶片载荷的调整策略为：在靠近叶尖附近，提高叶片前缘载荷以减小叶片吸力面的静压，提高进口相对马赫数，减小叶片中部的载荷峰值大小以减小压力面的逆压梯度，降低附面层分离的风险，由于原型压气机转子靠近叶片尾缘处的载荷较小，在改型时提高了尾缘处的载荷以增加加功量；转子叶片中部以下的载荷调整保持原始载荷分布形式不变，对载荷沿轴向的分布曲线进行光顺，使得载荷沿流动方向变化较为平缓，减小逆压梯度导致的附面层损失。静子叶片的调整策略为：不改变原型的载荷分布形式，减小各个截面上的载荷峰值大小，同时对载荷曲线进行光顺，使载荷更为均匀的加载到整个叶片。

图4　改型前、后3个不同半径处叶片型线对比

基于上述多叶排反问题载荷调整策略，本文采用样条曲线对原叶片表面轴向载荷分布进行重新构造。图5为3个不同径向位置处压力载荷曲线的对比，图中实线为改型设计所构造的载荷曲线，虚线为原型载荷曲线，圆圈为反问题计算得到的载荷曲线。从图中可以看出，改型后的载荷分布与给定的载荷定解条件吻合较好，反问题计算结果很好的满足了改型设计意图。与原型压气机载荷曲线相比，改型后的载荷曲线在保证了原有载荷分布形式的基础上更为光滑，变化更为平缓。图4为3个截面叶片型线改型前、后对比，可以看出，在载荷定解条件的驱动下，叶片型线较原型发生了改变。

图6为原型压气机与优化改型后的压气机在3个不同径向位置对马赫数等值线图对比。通过对比可以看出，在80%和50%2个径向位置处，由于改变了转子叶片前缘附近的载荷分布，使得叶片进口区域相对马赫数有所提升，相应提高了进口流量，同时按照激波理论，波前马赫数提高使得激波强度增强，因此压气机转子的增压能力有所增强。在20%径向位置处的叶片载荷调整量较小，故流场马赫数分布变化不大。由于在构造静子叶片的载荷时保证了原有的载荷分布形式，因此静子叶片通道内流动的马赫数分布未发生较大变化，由于上游转子叶片出口流场发生了改变，影响到了下游的静子叶片，为了保证给定的载荷分布，静子叶片的型线发生了一定改变。

图5　原始叶片构型、反问题输入以及反问题计算结果叶片3个不同半径处载荷分布曲线对比

图6　改型前、后叶片3个不同半径处相对马赫数分布等值线图对比

图7为改型后的叶片载荷分布等值线图，与原型对比可以看出，转子叶片叶尖处叶片前缘载荷有所提升，叶片中部的载荷峰值有所降低，激波位置与原型没有发生较大变化。叶片中部的载荷沿流动方向分布更加均匀，靠近尾缘处的载荷有所提升。静子叶片的载荷分布形式未发生较大变化，叶片前部载荷最大值有所减小，但高载荷区域面积较原型有所增大。从叶片载荷分布来看，通过反问题计算，叶片表面载荷分布基本满足了初始设计意图。

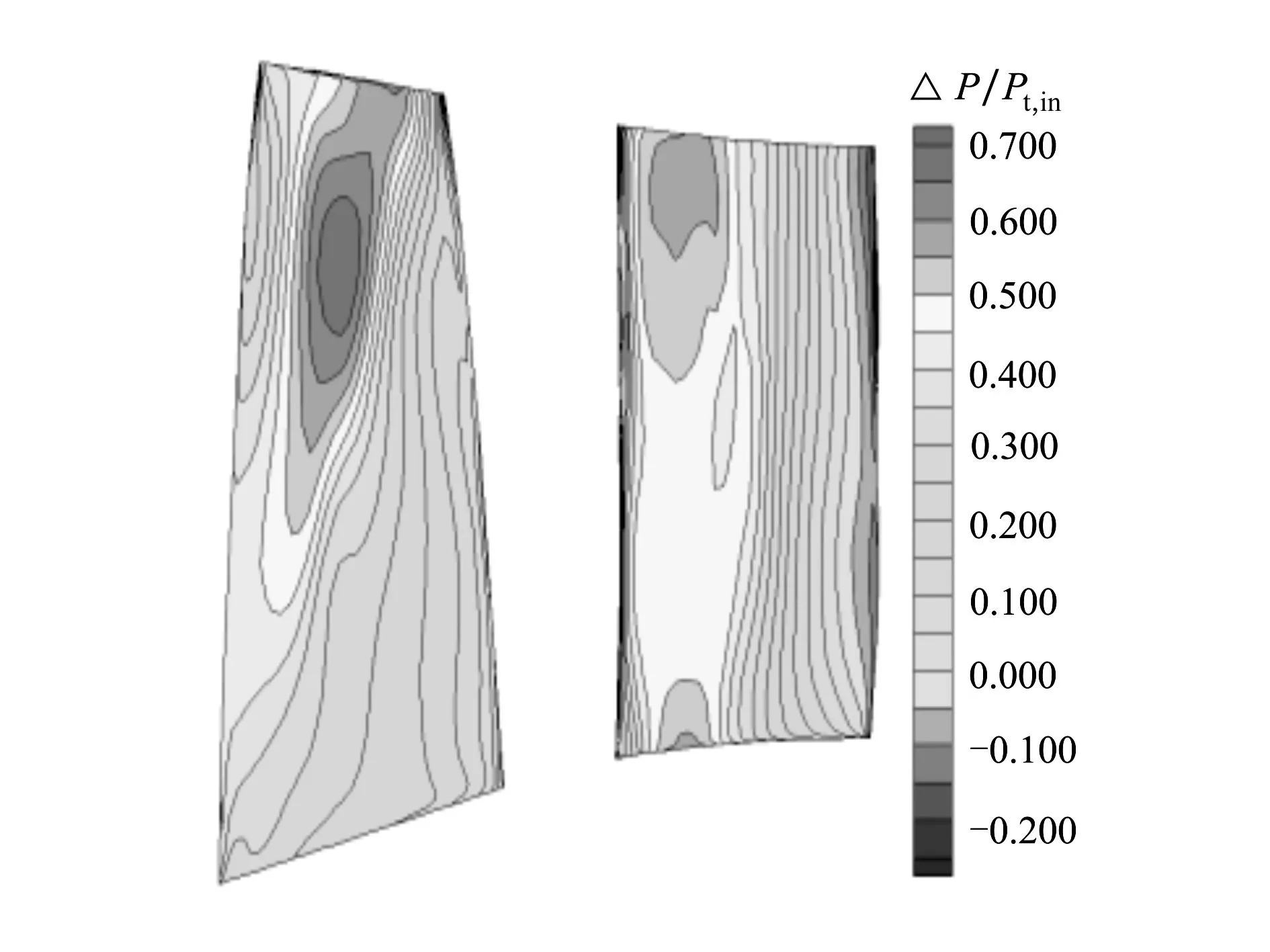
图7　改型后叶片表面载荷分布等值线图

参数原型改型流量/(kg·s-1)17.3217.93总压比1.5521.584效率0.9050.901

表3为改型前、后压气机出口截面气动性能参数对比，可以看出，由于提高了进口相对马赫数，转子的流通能力增强，流量比原型提高了3.5%，同时进口相对马赫数提高使得激波强度增大，提升了转

子的增压能力，压比较原型提高了2.0%。随着流量和压比的提高，压气机转子负荷增大，因此绝热效率有所下降，但下降幅度较小。从工程实用的角度出发，整个单级压气机的气动性能有明显提升。

3结论

本文以反问题设计理论为基础，发展了跨声速压气机多叶排三维黏性反问题改型设计方法，在运用实验结果验证了该程序的正确性后，将其运用到单级跨声速压气机多叶排改型设计上，通过对比，得出以下结论：

1) 本文所发展的正问题求解器所计算出的单级跨声速压气机气动特性与实验值符合较好，证明了正问题求解器特别是掺混面处理方法的可靠性。

2) 从叶片返回实验的结果可以看出，反问题计算的能够较好的还原原始叶片几何构型，验证了本文所采用的反问题计算方法是正确有效的。

3) 通过对叶片表面轴向载荷分布进行合理调整，能够有效提升压气机进口相对马赫数，从而增大压气机流通能力和激波强度，提高压气机的流量和压比。文中算例改型后的压气机流量提高了3.5%，压比增加了2.0%，而效率基本不变，改型设计提高了压气机转子的气动性能。

参考文献：

[1]Denton J D. The Calculation of Three-Dimensional Viscous Flow through Multistage Turbomachines[J]. ASME Journal of Turbomachinery, 1992, 114(1): 18-26

[2]Dang T Q. A Fully Three-Dimensional Inverse Method for Turbomachinery Blading in Transonic Flows[J]. ASME Journal of Turbomachinery, 1993, 115(2): 354-361

[3]Ahmadi M, Ghaly W. Aerodynamic Inverse Design of Turbomachinery Cascades Using a Finite Volume Method on Unstructured Meshes[J]. Inverse Problems in Science and Engineering, 1998, 6(4):281- 298

[4]Qiu X, Dang T. 3D Inverse Method for Turbomachine Blading with Splitter Blades[R]. ASME-2000-GT-0526

[5]周新海, 朱方元. 求解叶栅跨音速流动反问题的有限体积方法[J]. 工程热物理学报, 1985, 6(4):331-335

Zhou Xinhai, Zhu Fangyuan. Finite Volume Method to Solve The Inverse Problem for Transonic Flows in Cascades[J]. Journal of Engineering Thermophysics, 1985, 6(4):331-335 (in Chinese)

[6]杨策,老大中,蒋滋康. 求解跨声速压气机叶栅黏性流动反问题的数值解[J]. 推进技术, 1999,20(4):57-60

Yang Ce, Lao Dazhong, Jiang Zikang. Numerical Soluation on Viscous Inverse Problem for Transonic Compressor Cascades[J]. Journal of Propulsion Technology, 1999, 20(4): 57-60 (in Chinese)

[7]王正明,贾希诚. 正反问题数值解法相结合三维叶片的优化设计[J]. 工程热物理学报, 2000, 21(5): 567-569

Wang Zhengming, Jia Xicheng. Optimum Design of Three-Dimensional Blades by Combination of Numerical Methods for Solving Direct and Inverse Problems[J]. Journal of Engineering Thermophysics, 2000, 21(5): 567-569 (in Chinese)

[8]Wang Zhengming, Cai Ruixian. A Three-Dimensional Inverse Method Using Navier-Stokes Equation for Turbomachinery Blading[J]. Inverse Problems in Engineering, 2000(8): 529-551

[9]杨金广. 叶轮机械全三维黏性反方法设计技术研究[D]. 西安:西北工业大学, 2013

Yang Jinguang. Fully Three Dimensional Viscous Inverse Method for Turbomachinery Aerodynamic Design[D]. Xi′an: Northwestern Polytechnical University, 2013 (in Chinese)

[10] van Rooij M P C, Dang T Q, Larosiliere L M. Enhanced Blade Row Matching Capabilities via 3D Multistage Inverse Design and Pressure Loading Manager[R]. ASME Paper GT2008-50539, 2008

[11] Giles M B. Nonreflecting Boundary Conditions for Euler Equation Calculations[J]. AIAA Journal, 1990, 28(12): 2050-2058

[12] Chima R V. Calculation of Multistage Turbomachinery Using Steady Characteristic Boundary Conditions[R]. AIAA-1998-0968

[13] 刘昭威, 吴虎. 改进的反问题边界条件在叶轮机械中的应用[J]. 工程热物理学报, 2015, 36(10): 1-5

Liu Zhaowei, Wu Hu. Application of Improved Inverse Method Boundary Condition in Turbomachinery[J]. Journal of Engineering Thermophysics, 2015, 36(10): 1-5 (in Chinese)

[14] Dunker R, Rechter H, Starken H, et al. Redesign and Performance Analysis of a Transonic Axial Compressor Stator and Equivalent Plane Cascades with Subsonic Controlled Diffusion Blades[J]. Journal of Engineering for Gas Turbines and Power, 1984, 106(2): 279-287

[15] 刘昭威, 吴虎, 唐晓毅. 基于反问题设计方法的叶栅激波损失控制[J]. 推进技术, 2014,35(6):766-773

Liu Zhaowei, Wu Hu, Tang Xiaoyi. Numerical Soluation on Viscous Inverse Problem for Transonic Compressor Cascades[J]. Journal of Propulsion Technology, 2014,35(6): 766-773 (in Chinese)

Optimization of Transonic Axial Compressor Using Multi-Row Inverse Method

Liu Zhaowei, Wu Hu, Tang Xiaoyi

(Department of Aero-Engines, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:In order to improve the aerodynamic performance of transonic compressor, a compressor inverse design program is developed based on the turbomachnary three-dimensional viscous inverse design method theories. The numerical solution methods of Multi-Row transonic axial compressor flow field are introduced first and then the inverse design method and process is described in detail. The DLR R030-SUKS/31 single-stage transonic axial compressor experimental data are used to validate the calculation results. On the basis of the analysis of original blade loading distribution, the blade geometry is redesigned by applying the inverse method with the modified loading distribution. The numerical results show an increase in the compressor inlet Mach number. The mass flow rate and pressure ratio are increased respectively by 3.5% and 2.0%. Better performance of the redesigned compressor is achieved; this demonstrates the effectiveness of this method.

Keywords:inverse method, loading distribution, optimization design, transonic compressor

中图分类号：V235.13

文献标志码：A

文章编号:1000-2758(2016)01-0118-07

作者简介：刘昭威(1986—)，西北工业大学博士生，主要从事叶轮机械气动热力学的研究。

基金项目：国家自然科学基金(51076131)资助

收稿日期：2015-04-23