基于非线性收敛因子的Terminal滑模制导律设计

刘明雍, 张小件, 李洋

(西北工业大学 航海学院,陕西 西安　710072)



基于非线性收敛因子的Terminal滑模制导律设计

刘明雍, 张小件, 李洋

(西北工业大学 航海学院,陕西 西安710072)

摘要：水下动能武器在末端时刻攻击目标具有作战范围小,时间短的特性。传统滑模变结构制导律通常选取线性滑动平面,收敛速度慢,对收敛时间没有约束,不能满足系统快速收敛到平衡状态。针对这一问题,提出一种改进的Terminal滑模变结构控制方法,通过引入非线性因子,使系统跟踪误差快速收敛到零,保证系统以期望的有限时间收敛到平衡状态。采用Terminal滑模面结合指数趋近律设计有限时间快速收敛制导律,该制导律即能满足系统快速性收敛要求,又能离线计算收敛时间。理论分析表明:所设计的制导律满足系统稳定性要求,并仿真验证了其快速收敛的有效性,较传统变结构制导方法收敛速度更快,具有更强的鲁棒性。

关键词：Terminal滑模面；变结构控制；制导律；动能武器

当今乃至未来的海战是一个水下武器对抗的时代,为了提高自身的安全性,针对外来的攻击,各国海军竞相发展出了攻击或拦截外来武器的动能武器[1]。水下动能武器具有体积小、速度高、攻击距离短、制导系统反应时间短等特点,要求制导武器系统要有快速的系统收敛及直接命中目标的特性。

当制导武器攻击目标时,不仅希望系统能够快速收敛到平衡状态,以便有足够的时间应对目标机动;同时希望获得较小的脱靶量,以直接命中目标,达到毁伤的效果。因此,本文在设计制导律的过程中主要考虑两方面的因素:有限时间收敛和脱靶量为零。有限时间收敛能够保证系统快速响应目标机动;脱靶量为零能够保证直接命中目标,获得最大的毁伤效果。

有限时间收敛即制导系统在有限时间内达到平衡状态作为制导武器实现攻击目标的一个重要研究方面。以往学者对有限时间收敛做了不少的研究工作。其中,文献[2]提出了一种时间收敛的滑模变结构制导律,该制导律能够保证系统在攻击目标末端命中时刻收敛到平衡状态。文献[3]对二阶非线性不确定系统设计滑模面,保证了输出跟踪误差有限时间收敛到零。文献[4]针对不确定非线性系统提出了动态滑模控制,保证了系统在一定时间内收敛。以上文献[3-4]都需要跟踪误差模型具有二阶甚至高阶连续可导,且有限时间“较长”。另外,根据滑模面的收敛特性,有学者们提出了在滑模面中引入非线性项以提高系统的收敛特性,缩短收敛时间[5]。文献[6]从碰撞时间入手,提出基于非线性理论设计的满足碰撞时间的制导律,该制导律不同于以递归和数值解的方法求解碰撞时间,而是通过反馈闭环系统求出精确的碰撞时间,对于具有延迟的制导与控制系统达到了较好的估计、补偿效果。文献[7]综合考虑自动驾驶仪动态特性及系统的不确定性,提出一种时间收敛的制导律。该制导律通过在有限的时间内估计目标机动信息,然后根据估计获得的目标机动信息设计满足时间收敛的滑模变结构制导律。一定程度上补偿了由自动驾驶仪的动态特性和系统不确定性带来的误差。文献[8]通过改变Terminal滑模面的非线性项,避免了奇异点的出现。

在本文中,从系统快速收敛这一角度提出了一种基于非线性收敛因子的Terminal 滑模控制制导律,通过引入非线性因子,改变滑模面参数,保证制导系统能够在期望的有限时间内以任意初始状态收

敛到平衡状态,并且收敛时间能够通过滑模参数离线计算出来。结合本文的滑模面推导出了动能武器末端制导律,通过仿真分析该制导律能够以期望的有限时间使制导系统达到平衡状态,从而直接命中目标,而且对外界干扰具有很强鲁棒性。

1问题描述

水下动能武器在攻击或拦截目标时,由于主要是靠动能毁伤,要求动能武器能直接命中目标。而在攻击目标的过程中,目标可能存在机动,要求动能武器具有应对目标机动的快速收敛方法。即主要从脱靶量和收敛时间对本文制导律进行分析设计。

考虑到弹目相对运动关系。弹目相对运动方程可以解耦为俯仰平面和偏航平面的2个分量运动,本文只考虑俯仰平面内的运动,如图1所示。

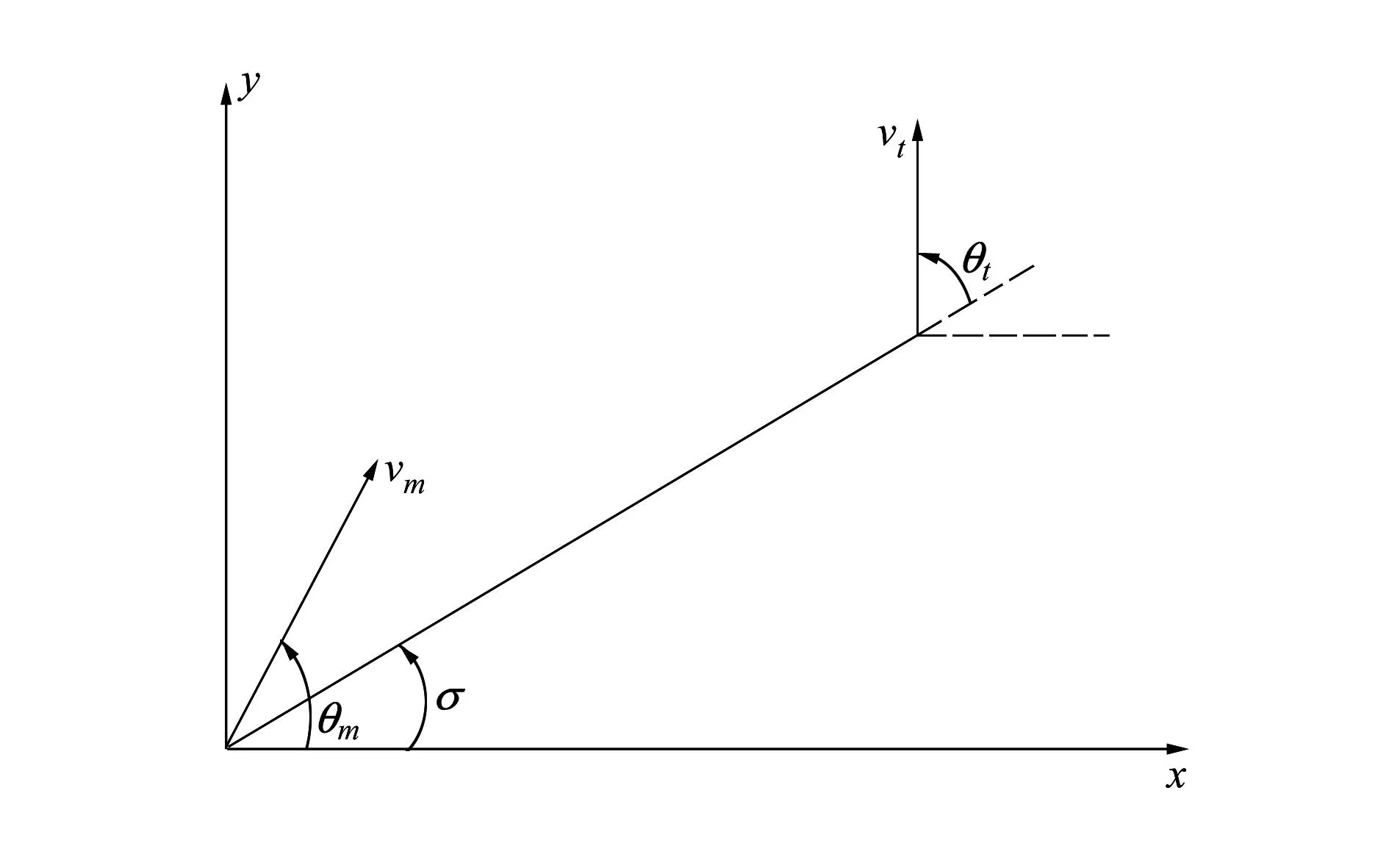
图1　弹目相对运动几何关系图

假设动能武器速度和目标速度均为常量,分别为vm、vt,且动能武器速度大于目标速度。其中θm、θt分别为动能武器与目标的航向角;σ为视线角,即二维平面内拦截器与视线角之间的连线与水平方向上的夹角,其变化率为零表明动能武器能够击中目标。

根据弹目相对几何关系可知

(1)

(2)

(3)

式中：r(t)为动能武器与目标相对距离,u=aA(t)为动能武器控制输入,即本文要设计的制导律;at为目标过载,这里可视为干扰。

(4)

2有限时间收敛

2.1有限时间收敛概念

对于非线性系统:

(5)

式中，f:U0×R→Rn在U0×R上连续,且U0为原点x=0的一个开邻域,f(0,t)=0。系统的平衡点x=0有限时间收敛,对于任意给定的初始时刻t0所对应的初始状态x(t0)=x0∈U,存在一个依赖于x0的时间T≥t0,使得系统方程以x0为初始状态的解x(t)=φ(t:t0,x0)有定义,并且:

(6)

当时间t∈[t0,T)时,φ(t:t0,x0)∈U/0。此系统的平衡点x=0有限时间稳定,是指它是Lyapunov稳定和在原点的一个邻域U∈U0内有限时间收敛。如果U=Rn,那么系统在全局范围内有限时间收敛[9]。

2.2Terminal滑模面

传统滑模面收敛特性主要取决于趋近律的选取,且没有时间约束,并存在很大抖动,不能满足系统快速性收敛的要求,同时抖动给系统的稳定性带来一定影响。为此,基于传统滑模面原理,有学者在滑模面种引入非线性项,以改变系统的收敛特性[10]:

若定义滑模面s1

(7)

其收敛时间

(8)

滑模面s2

(9)

其收敛时间

(10)

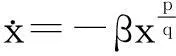
2.3改进的滑模面

为了证明改进的滑模面的收敛速度优于传统Terminal滑模面,首先介绍以下定理:

定理1[10]对于非线性系统

(11)

式中。φ(x)在C(-∞,∞)有定义,并满足φ(x)>-β,且q>p,都为奇整数。则系统(11)是渐进稳定的,且对于任意初始状态x(t0)≠0,系统都能在有限时间内达到平衡点。

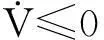
稳定性证明

令

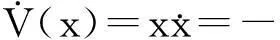
命题1 假设φ(x)在c(-∞,∞)有定义,并满足φ(x)≥0。当|x|≥1时,如果φ(x)≥

α|x|(q-p)(1+ε)/q(其中q>p>0,且都为奇整数; α,β,ε>0)。对于任意初始状态x(t0)≠0,系统(11)有限时间稳定,且对于任意初始状态x(t0)收敛时间是有界的。

证明从定理1可以明显得出系统(7)是稳定的,下面主要考虑收敛时间。

由φ(x)≥α|x|(q-p)(1+ε)/q可知

(12)

令x=yq/(q-p),则

(13)

定义

当|x|>1时

(14)

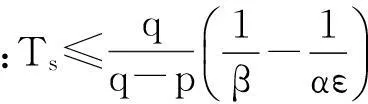
证毕,即系统有限时间收敛。

3制导律设计

根据前文分析,选取滑模面

(15)

式中，m>n>0,q>p>0,且都为奇整数;α,β,γ>0。

取趋近律:

(16)

式中，k1,k2>0。

对(15)式进行微分得:

(17)

结合(4)式、(16)式及(17)式可得制导律表达式

(k1s+k2sgn(s))r+at

(18)

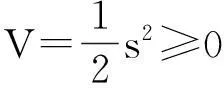
4仿真及结果分析

本节将比较本文所设计的快速Terminal滑模变结构制导律与传统滑模变结构制导律。从目标静止和目标机动2种情况进行分析。

4.1目标静止

假设动能武器以50 m/s的速度航行攻击目标,初始位置M(x0,y0)=M(0,0),初始航向角为0°;目标初始位置 T(x0,y0)=T(300,400)。仿真中选择合适的参数:m=5,n=3,q=3,p=1,α=2,β=0.03,γ=0.1,k1=k2=0.01,仿真步长取0.01s。仿真结果如图2～图4所示(其中实线表示基于Terminal滑模变结构制导律仿真结果,虚线表示基于传统滑模面变结构制导律仿真结果)。

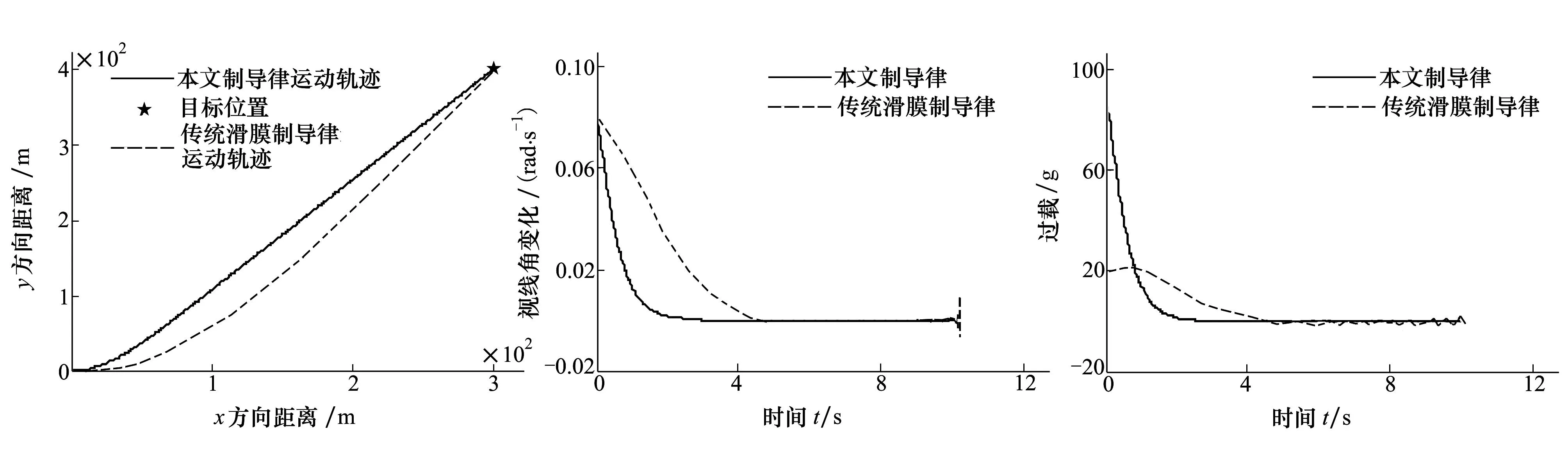
图2　动能武器运动轨迹　　　　　　　图3　视线角变化率曲线图4　动能武器过载随时间变化曲线

4.2目标机动

假设动能武器以50 m/s的速度航行,初始位置M(x0,y0)=M(0,0),初始航向角为0°;目标航行速度30 m/s,初始位置T(x0,y0)=T(300,400),初始航向角为180°,目标做10*rand(1)随机机动。仿真中各参数同目标静止时选取同样的数值,仿真步长取0.01 s。仿真结果如图5～图7所示。

图5为过载随时间变化曲线,虽然目标处于随机机动状态,动能武器在制导律(18)的作用下相应进行调整轨迹,以保证命中目标,但是动能武器过载基本稳定在某一范围内;图7对应的是视线角变化率随时间变化曲线,从图5和图7中可以看出,拦截器在2 s左右达到了收敛状态,较传统滑模控制具有更快的收敛速度,且抖动更小。从图6运动轨迹可以看出,本文制导律能随目标机动做出快速的响应,为动能武器在后期拦截目标的过程中提供充足的应变时间。能够有效拦截目标。

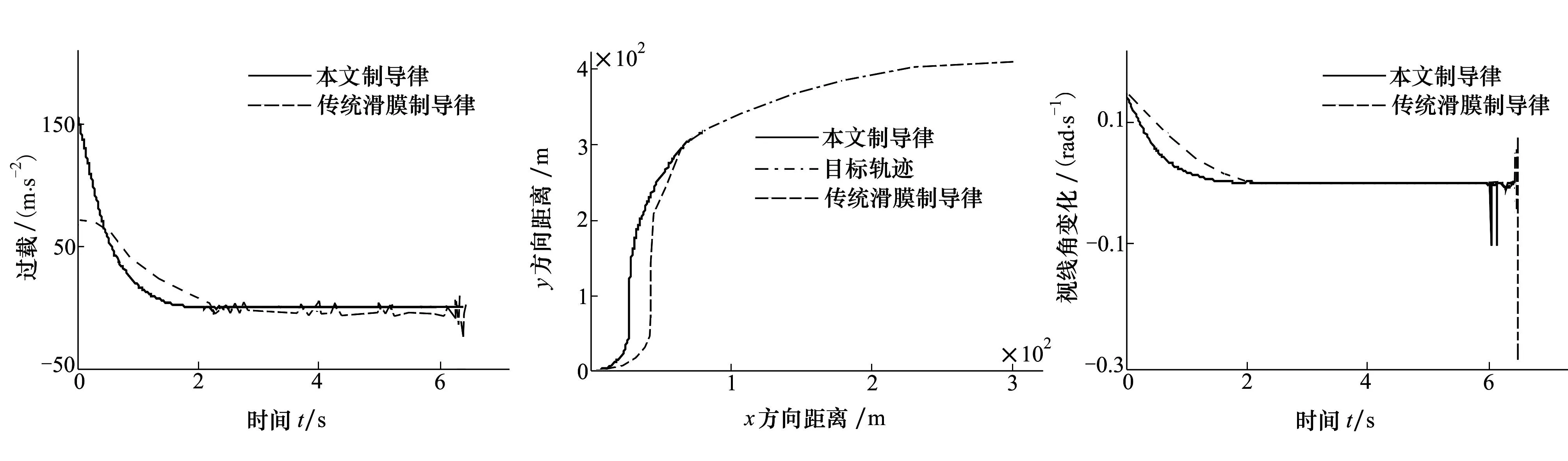
图5　动能武器过载变化曲线　　　　　　　图6　运动轨迹图7　视线角变化率随时间变化曲线

5结论

参考文献：

[1]严卫生, 任章, 徐德民, 等. 迎面拦截变结构导引律及其应用研究[J]. 西北工业大学学报, 2000, 18(4): 616-620

Yan Weisheng, Ren Zhang, Xu Demin, et al. A Head-on Impact Variable Structure Guidance Law[J]. Journal of Northwestern Polytechnical University, 2000, 18(4): 616-620 (in Chinese)

[2]Zhang Y, Sun M, Chen Z. Finite-Time Convergent Guidance Law with Impact Angle Constraint Based on Sliding-Mode Control[J]. Nonlinear Dynamics, 2012, 70(1): 619-625

[3]Kaiyu Z, Hongye S U, Keqin Z, et al. Adaptive Terminal Sliding Mode Control for High-Order Nonlinear Dynamic Systems[J]. Journal of Zhejiang University Science, 2013, 4(1): 58-63

[4]Liu J, Sun F. A Novel Dynamic Terminal Sliding Mode Control of Uncertain Nonlinear Systems[J]. Journal of Control Theory and Applications, 2007, 5(2): 189-193

[5]Slotine J J E, Li W. Applied Nonlinear Control[M]. Englewood Cliffs, NJ: Prentice-hall, 1991

[6]Saleem A, Ratnoo A. A Nonlinear Guidance Law for Impact Time Control[C]∥American Control Conference (ACC), 2015: 651-656

[7]Li G L, Yan H, Ji H B. A Guidance Law with Finite Time Convergence Considering Autopilot Dynamics and Uncertainties[J]. International Journal of Control, Automation and Systems, 2014, 12(5): 1011-1017

[8]汤一华, 陈士橹, 徐敏, 等. 基于Terminal滑模的动能拦截器末制导律研究[J]. 空军工程大学学报: 自然科学版, 2007, 8(2): 22-25

Tang Yihua, Chen Shilu, Xu Min, et al. Terminal Guidance Law of Kinetic Interceptor Based on Terminal Sliding Mode[J]. Journal of Air Force Engineering Uuniversity: Natural Science Edition, 2007, 8(2): 22-25 (in Chinese)

[9]Zhang Y, Sun M, Chen Z. Finite-Time Convergent Guidance Law with Impact Angle Constraint Based on Sliding-Mode Control[J]. Nonlinear Dynamics, 2012, 70(1): 619-625

[10] Tie L, Cai K Y. A General Form and Improvement of Fast Terminal Sliding Mode[C]∥Intelligent Control and Automation (WCICA), 2010 8th World Congress on IEEE, 2010: 2496-2501

Nonlinear Convergence Factor Terminal Mode Based Guidance Law Design

Liu Mingyong, Zhang Xiaojian, Li Yang

(College of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China)

Abstract:Kinetic weapon attack targets underwater with small range operations, short time features at the end of the time. Traditional linear sliding mode control guidance law can not meet the system in a finite time fast convergence to equilibrium requirements, that can not ensure attacking the target effectively. To solve the problem, this paper proposes an improved Terminal Sliding Mode Control method, guarantee system convergence to equilibrium state in finite time, by introducing nonlinear factor, make the system tracking error converge to zero quickly. By combining with exponential reaching law Terminal sliding mode surface design limited time fast convergent guidance law. The guidance law can ensure that the system convergence to equilibrium fast and calculate convergence time off-line. Theoretical analysis, the designed guidance law can meet the requirements of the system′s stability, and its effectiveness was verified through simulation, and its convergence time is faster than traditional variable structure guidance law, has stronger robustness.

Keywords:Calculations, computer simulation, convergence of numerical methods, design, electronic guidance systems, Lyapunov methods, robustness(control systems), sliding mode control,stability,trajectories, variable structure control; guidance law, Kinetic weapons, terminal sliding mode

中图分类号：V448.234

文献标志码：A

文章编号:1000-2758(2016)01-0047-06

作者简介：刘明雍(1971—)，西北工业大学教授、博士生导师，主要从事航行器制导与控制研究。

基金项目：国家自然科学基金(51109179、51379176、61473233)资助

收稿日期：2015-10-09