基于灰色神经网络的S700K转辙机故障诊断方法研究
2016-05-07王瑞峰陈旺斌
王瑞峰,陈旺斌
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
随着铁路向高速、重载快速发展,S700K转辙机大量投入使用,这就需要更加完备的运行状态监测机制和智能化的故障诊断方法来提高设备的安全性和可靠性。长期以来,对转辙机故障诊断及定位的分析仅依靠维修工作人员的专业知识和经验,微机监测系统采集的信息仅作为人工判断故障的依据,故障识别时间较长,且误判、漏判现象时有出现。因此,研究通过功率曲线判断故障的智能诊断方法具有重要意义。
目前,研究应用于S700K转辙机的故障诊断方法中,没有充分利用微机监测系统采集的反映设备运行状态的最优信息,且各诊断方法均有其局限性。广泛研究使用的专家系统[1]知识获取困难,神经网络[2]需要大量训练样本,支持向量机[3]原则上只能进行两两分类,贝叶斯网络[4]需要提供可靠合理的先验概率,而它的确定非常困难。
本文结合灰色关联分析方法[5,6]和神经网络模型建立灰色神经网络[7,8],利用微机监测系统提供的S700K转辙机动作功率曲线,实现转辙机的故障诊断。该方法克服了单独灰色关联分析和神经网络建模的缺陷,实现了二者的优势互补,经验证有效提高了设备的故障识别率。
1 S700K转辙机动作过程的数据分析
1.1 功率曲线与运行状态的关系
S700K转辙机采用三相交流异步电机,其输出功率P和输出拉力F分别为
( 1 )
( 2 )
由式( 1 )、式( 2 )可得
( 3 )
式中:U为电动机电压;I为电动机电流;η为电动机效率;cosθ为电动机功率因数;Re为转辙机传动系统等效力臂;n为电动机转速[9]。
由式( 3 )可知,S700K电动转辙机功率的大小可以反映其输出拉力的变化值。根据S700K转辙机设计原理,转辙机各零部件的机械强度、工作寿命,都是根据转辙机设计的最大工作拉力乘以安全系数进行计算的,所以转辙机的工作状态就是其输出工作拉力的变化状态[10-12]。
综上可知,S700K转辙机功率值反映道岔尖轨推拉力的大小,而该拉力值反映转辙机的运行状态,所以通过分析微机监测系统采集到的对应道岔的动作功率曲线可准确判断转辙机的运行状态。
1.2 正常动作功率曲线分析
S700K转辙机正常动作功率曲线如图1所示,功率值在0.15 s左右上升并很快达到最大值,此段为转辙机启动阶段,之后随着设备的运行,其输出功率急剧下降并趋于稳定,转辙机动作杆带动道岔尖轨进行解锁和转换,待道岔转换完毕,转辙机的输出功率出现一定幅度的下降,但不会降为零,之后随着道岔位置的给出,相应电路被断开,功率值降为零。

图1 S700K正常动作功率曲线
1.3 故障功率曲线分析
经过现场调研和查阅相关资料,目前上道使用的S700K转辙机常见故障模式主要有8种,其故障现象和故障原因见表1,相应故障下对应的输出功率曲线如图2所示,其中功率值测量精度为±2%,符合信号微机监测系统技术条件[13]。

表1 S700K电动转辙机常见故障分析
2 故障识别系统总体设计
S700K转辙机故障识别系统原理如图3所示,主要包括标准故障特征集的建立和灰色神经网络的建立两部分。其中微机监测系统的道岔监测模块为故障诊断提供数据来源,灰色神经网络计算标准故障曲线和待检故障曲线的灰色关联度值,最后对计算得到的关联度值进行大小排序,最大值对应的曲线类型即为该待检曲线的故障类别。

图2 常见故障所对应的功率曲线

图3 故障识别原理图
3 基于灰色神经网络的故障识别方法
3.1 标准故障特征集的建立
根据转辙机动作各阶段的功能及其对应功率值的大小,将功率曲线分为启动、解锁、转换、锁闭和表示5段。读取每一段中功率的最大值、最小值并求其平均值,以每一段的最大功率值、最小功率值、功率平均值和时间长度作为反映该段曲线的特征数据。将转辙机正常动作功率曲线故障代码记作f0,可得到故障诊断特征数据集,见表2。

表2 S700K电动转辙机常见故障特征数据
3.2 灰色神经网络的建立
灰色关联分析的基本思想是根据序列几何形状的相似程度来判断其联系是否紧密。曲线越接近,相应序列之间的关联度就越大,反之越小[6]。
利用灰色关联分析算法进行故障诊断,首先要建立故障诊断特征集,存储标准故障参考模式数据,然后提取待检样本相应的特征值,计算待检样本与各标准故障模式的关联度值,最后根据关联度值的大小识别待检曲线的故障模式。具体步骤如下:
步骤1确定标准故障特征矩阵X和待检特征向量Y。
由表2数据可建立如下所示的特征矩阵,其中m=8为故障模式个数,n=20为每个故障模式的特征向量维数。
( 4 )

( 5 )
步骤2求初值像。
( 6 )
( 7 )
步骤3求序列差、最大差和最小差。
Δi(k)=|xi′(k)-y′(k)|
( 8 )
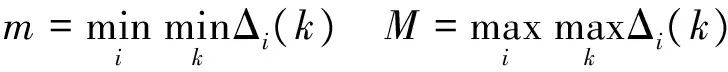
( 9 )
步骤4计算关联系数。
(10)
式中:ε为分辨系数,ε∈(0,1)。
步骤5计算关联度。
(11)
步骤6按关联度排序。
由式(11)可得待检曲线与9类模式曲线的关联度值,可表示为式(12)所示的序列,对该序列各数值进行排序,其中最大值对应的模式即为当前待检样本的故障类型。
γ=[γ0γ1…γm]
(12)
灰色关联分析方法通过定量计算数值实现定性的结果分析,诊断结果可靠。但其并行处理能力弱,当特征向量维数大于3时计算复杂。而神经网络具有很强的并行计算能力,所以将灰色关联分析与神经网络相结合形成灰色神经网络,用神经网络进行灰色关联度的计算,可以实现二者的优势互补。
设计如图4所示的自定义神经网络模型,计算待检样本曲线和标准故障数据的灰色关联度值。所建网络由三层组成,其中第一层作为输入数据缓冲器,输入X和Y并作无量纲处理,其节点数为特征向量的分量个数,共20个神经元;第二层作为中间数据存储器,其节点数为标准曲线类型个数,共9个神经元;第三层输出灰色关联度值,其节点数为曲线类型数,共9个输出神经元。第一层与第二层之间以式( 8 )为映射函数,第二层与第三层间的映射函数为灰色关联度的计算式,即以式(10)和式(11)为激励函数。各层的阈值和权值分别设为0和1。

图4 灰色神经网络
3.3 实例验证及结果分析
从微机监测系统获取转辙机当前运行状态下的功率曲线,按图5所示流程计算该待检样本与故障诊断特征集各模式特征值的灰色关联度值,最大灰色关联度值所对应的曲线模式即为当前转辙机的故障类型。

图5 故障诊断流程框图
以标准故障诊断特征集中9种曲线模式数据为训练样本确定分辨系数ε的取值。分别计算ε以0.01为步长从0到0.99时该诊断网络的故障识别率,可以得到故障正确识别率结果,如图6所示。由图6可知,分辨系数ε=0.48附近,诊断网络的正确识别率最高,其最大值为95.9%。
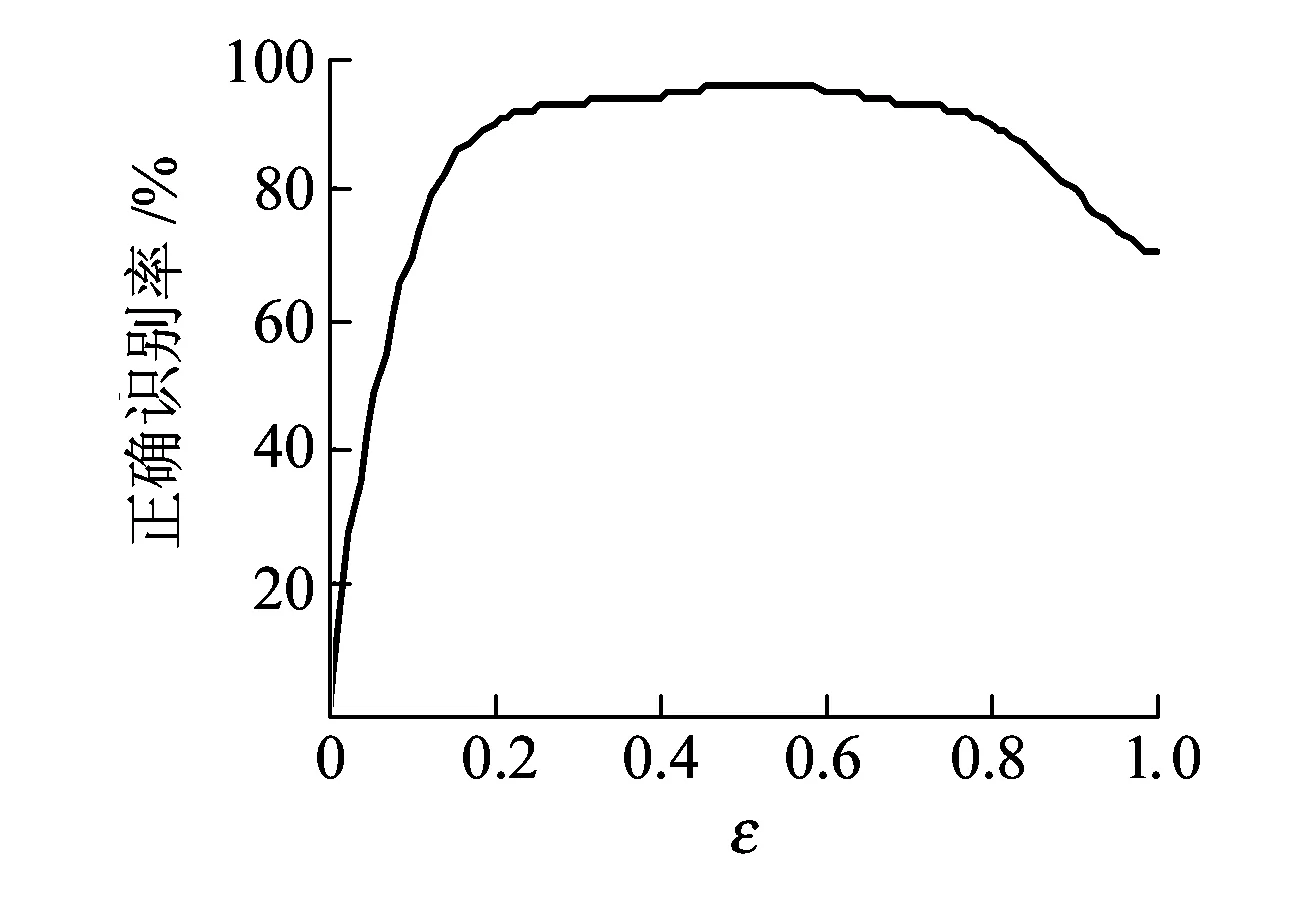
图6 不同分辨系数下的识别率
图7为武广长沙电务段管辖内某一道岔对应的S700K转辙机发生故障时的功率曲线,将该曲线作为待检样本,提取其特征数据见表3,按式( 7 )进行数据无量纲处理得到特征值见表4。

图7 现场某S700K转辙机发生故障时对应的功率曲线

i特征值Pimax/kWPimin/kWPi/kWTi/s1207010306620570490440673061049056271412205092095512912212515

表4 待检曲线特征值
按图5所示流程,取ε=0.48,计算得到灰色关联度值见表5,其中最大关联度值所对应的曲线为标准特征集中的曲线f5,该曲线故障为道岔不能锁闭空转,与现场检修结果一致。

表5 关联度值序列
为了测试该诊断方法的故障识别性能,从微机监测系统中新获取48条S700K转辙机动作形成的功率曲线作为待检样本,按图5所示流程进行故障诊断,计算得到正确识别率为95.8%,误识率为0%,拒识率为4.2%。
4 结论
本文通过分析交流转辙机功率曲线与动作过程的关系,说明功率曲线能反映转辙机的运行状态,提取功率曲线特征量将其作为诊断对应设备故障类型的数据,比已有仅针对电流电压数据的分析方法更能反映设备故障机理。建立灰色神经网络模型,计算待检曲线和故障特征集中各曲线间的灰色关联度值,通过灰色关联度值的大小确定待检曲线的故障类型,定量计算有效提高了故障识别率。结果表明,该方法无需训练,诊断结果准确性高,故障识别率可达95.8%,为S700K转辙机故障诊断提供了理论依据。
后续可对将S700K转辙机的动作功率和电流等参数结合进行故障诊断的灰色神经网络方法,及将不同灰色关联分析方法与神经网络相结合用于S700K转辙机的故障诊断方法进行研究。
参考文献:
[1]ATAMURADOV V,CAMCI F,BASKAN S,et al.Failure Diagnostics for Railway Point Machines Using Expert Systems[C]//IEEE International Symposium on Diagnostics for Electric Machines,Power Electronics and Drives.New York:IEEE Press,2009:1-5.
[2]王铁军,董昱,马彩霞,等.基于BP神经网络的道岔智能故障诊断方法[J].铁道运营技术,2011,17(2):4-7.
WANG Tiejun,DONG Yu,MA Caixia,et al.Intelligent Turnout Fault Diagnosis Based on BP Neural Network[J].Railway Operation Technology,2011,17(2):4-7.
[3]王思明,雷华.一种基于LS-SVM的道岔控制电路故障诊断[J].兰州交通大学学报,2010,29(4):1-5.
WANG Siming,LEI Hua.Fault Diagnosis for Railway Switch Control Circuit Based on ARPSO Least Squares Support Vector Machine[J].Journal of Lanzhou Jiaotong University,2010,29(4):1-5.
[4]翟永强.贝叶斯网络在道岔控制电路故障诊断中的应用研究[D].兰州:兰州交通大学,2012.
[5]DENG J L.Control Problems of Grey Systems[J].Systems & Control Letters,1982,1(5):288-294.
[6]刘思峰,党耀国,方志耕,等.灰色系统理论及应用[M].北京:科学出版社,2010.
[7]袁景凌,钟珞,李小燕.灰色神经网络的研究及发展[J].武汉理工大学学报,2009,31(3):91-93.
YUAN Jingling,ZHONG Luo,LI Xiaoyan.The Research and Development of Grey Neural Network[J].Journal of Wuhan University of Technology,2009,31(3):91-93.
[8]姜波.灰色系统与神经网络分析方法及其应用研究[D].武汉:华中科技大学,2004.
[9]王耀杰,高晓丁,辛凯.信号设备非电量参数测试[M].北京:中国铁道出版社,2004:136-138.
[10]何攸旻.高速铁路道岔故障诊断方法研究[D].北京:北京交通大学,2014.
[11]赵林海,陆桥.基于灰关联的道岔故障诊断方法[J].铁道学报,2014,36(2):69-74.
ZHAO Linhai,LU Qiao.Method of Turnout Fault Diagnosis Based on Grey Correlation Analysis[J].Journal of the China Railway Society,2014,36(2):69-74.
[12]高晓丁,佟元江,王跃杰,等.电动转辙机工作特性分析[J].铁路通信信号,2001,37(1):23-25.
GAO Xiaoding,TONG Yuanjiang,WANG Yuejie,et al.Analysis of the Electric Switch Working Feature[J].Railway Signalling & Communication,2001,37(1):23-25.
[13]中华人民共和国铁道部.信号微机监测系统技术条件(暂行)[Z].北京:中国铁道出版社,2006.
