基于云模型和组合赋权法的CTCS-3级列控系统可靠性评价
2016-05-07张友鹏杨金凤
张友鹏,杨金凤
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
CTCS-3级列控系统作为高速铁路的“大脑和神经系统”,是确保列车安全、高效运行的关键。它由大量复杂的电子相关组件和计算机系统组成,是一个复杂的系统[1]。对于复杂系统而言,系统中部件、功能的故障时有发生,然而部分部件或功能的失效并不代表整个系统失效。因此,用系统绝对正常的平均故障间隔时间MTBF(Mean Time Between Failure)不能正确且客观地评价系统的可靠性。实际中人们更多关注的是系统能在多大程度上保持其规定功能的能力[2]。为此本文将从功能的角度出发,对CTCS-3级列控系统进行可靠性评估。
目前,故障树分析法FTA(Fault Tree Analysis)、马尔可夫模型(Markov)、模糊综合评判法(Fuzzy Comprehensive Evaluation Method)以及贝叶斯网络模型(Bayesian Network)是系统可靠性评估中常用的方法,已广泛应用于铁路信号系统[3-6]。对于复杂系统的可靠性综合评价,大都采用模糊综合评判法[7-9]。文献[10]提出的基于雷达图综合能力模型以及云模型的复杂系统可靠性综合评价方法在实际应用中最为广泛[11-13],但该方法在进行系统可靠性评价时,通过专家打分策略确定各基本单元的权重,没有充分考虑部件、功能的权重,降低了评估的准确性,且要求部件、功能的技术指标可实测和量化,使得该方法在实际应用中受到一定的限制。为此,本文提出基于云模型和组合赋权法的系统可靠性评价方法。
1 云模型基本理论
1.1 云的基本概念
云模型是一种定性与定量的转换模型,可以实现某个定性概念与定量数值之间的相互转换。设X是一个用精确数值表示的论域,X={x},A是与X相对应的定性概念,对于任意x∈X,若存在一个有稳定倾向的随机数y=μA(x),则称y为x对A的隶属度,而y在论域X上的分布称为隶属云,简称云[14]。云是论域X到区间[0,1]的映射,即
y=μA(x):X→[0,1] ∀x∈X,x→y
1.2 云的数字特征
云一般由期望Ex、熵En和超熵He3个数字特征来表征。期望值Ex反映了定性概念的信息中心值;熵值En是定性概念模糊度的度量,反映了在论域中被这个概念所接受的数值范围;超熵He反映了云滴的离散程度,超熵越大,云滴的离散程度越大,云的厚度也越大。它们将模糊性和随机性融合在一起,构成定性与定量的相互映射[15],隶属云及其数字特征如图1所示。
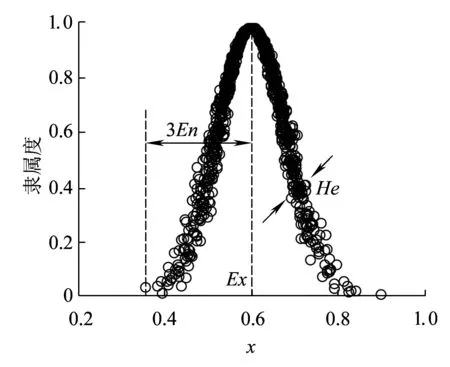
图1 隶属云及其数字特征
对于存在双边约束[Cmin,Cmax]的指标可以用云模型描述,相应的3个数字特征为
( 1 )
式中:k为常数,可以根据指标的不确定性和随机性具体调整。对于左右两极端的评价元素可用半云模型描述,期望值Ex分别取其左右约束,熵值En分别取相应对称云模型熵值的一半。
1.3 正态云模型
正态云是一种定性概念与定量表示之间的不确定转化模型,也是表达定性概念最常用的一种。其特点为对于某一定性概念,相应的云对位于Ex±3En之外的元素均可忽略。通过正向云算法,可以实现从定性概念到定量数据的映射;通过逆向云算法,可以实现从定量表示到定性概念的映射。正态云的生成算法如下[14]:
(1)xi=G(Ex,En)。生成以Ex为期望值,En为标准差的随机数xi。
(2)Eni=G(En,He)。生成以En为期望值,He为标准差的随机数Eni。
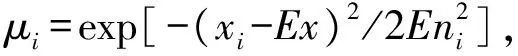
2 赋权方法简介
本文结合层次分析法和熵权法确定CTCS-3级列控系统各单元的权重值。
2.1 层次分析法
层次分析法AHP(Analytic Hierarchy Process)是一种定性与定量分析相结合的多目标决策方法。AHP将问题分解为若干组成因素,并按支配关系形成层次结构,然后应用两两比较法确定各因素的相对重要性[16]。AHP的实施流程为:(1)建立系统的层次结构模型;(2)构造判断矩阵;(3)一致性检验;(4)计算各因素的权重。
判断矩阵的构造是层次分析法的重点,通常采用9标度法(表1)将底层元素进行两两比较,从而确定判断矩阵中各元素的数值。
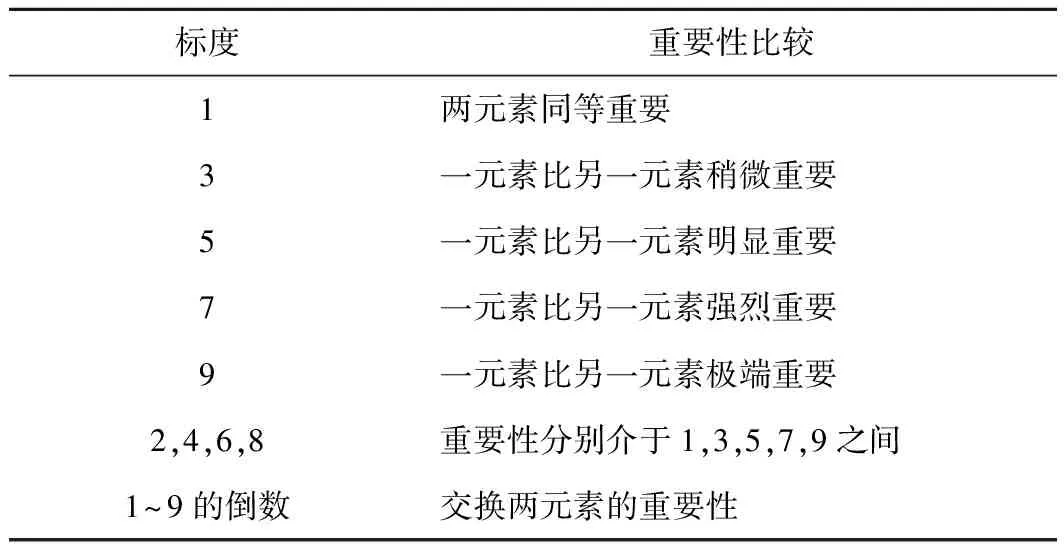
表1 9标度法
2.2 熵权法
信息论中熵是对不确定性的度量,信息量越大,则不确定性越小,对应的熵值也就越小。熵权法的实施流程包括以下4个步骤[17]:(1)构造判断矩阵X=(xij)m×n;(2)计算指标的熵值ej;(3)计算指标的变异系数hj;(4)计算熵权ωj。
第j个单元的熵值ej、变异系数hj、熵权ωj的计算公式为
( 2 )
式中:k为常数,为使ej∈[0,1],一般取k=(lnm)-1。
hj=1-ej
( 3 )
( 4 )
2.3 组合赋权法
组合赋权法将主观权重和客观权重有机地结合在一起,既可以反应决策者的主观意愿,又可以避免评价结果的主观随意性,使求得的权重更加科学合理。假设由层次分析法得到的各单元主观权重向量为WS,由熵权法求得的客观权重向量为WO。运用加法集成法求得最终的综合权重向量W为
W=αWS+βWO
( 5 )
式中:α,β为组合赋权法联系的待定系数。可用差异系数法进行求解[18]。
( 6 )
式中:Pi(i=1,2,…,n)为主观权重向量按升序排序后对应的分量;n为评价元素个数。
3 CTCS-3级列控系统可靠性评价
CTCS-3级列控系统是由GSM-R实现车-地信息双向传输,无线闭塞中心生成行车许可,轨道电路实现列车占用检查,应答器实现列车定位,并兼容CTCS-2级功能的列车运行控制系统。它由地面子系统和车载子系统组成,CTCS-3级列控系统结构示意图如图2所示[6]。其中,除人机界面、应答器接收模块及天线为双系冷备结构外,其余单元均为双系热备冗余结构(本文中列控车载设备采用CTCS3-300T)。
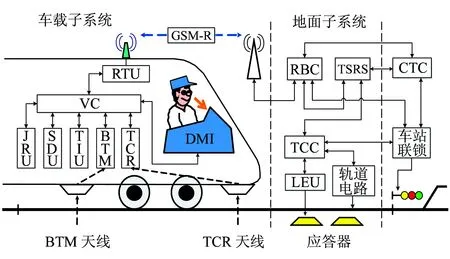
图2 CTCS-3级列控系统结构示意图
3.1 评价模型的构建
本文通过建立CTCS-3级列控系统的综合能力模型以及可靠性评价云模型,对其进行可靠性评价。
3.1.1 综合能力模型
CTCS-3级列控系统是实现列车安全运行的重要设备,将其从影响列车安全运行角度分类,可分为生成行车许可功能、车地信息传输功能、列车定位功能、列车运行监控功能以及人机交互功能,此外CTCS-3级列控系统还具有数据记录功能[19]。若用相对指标值表示上述6种功能对列控系统完成全部功能的贡献,从列车运行安全防护角度,建立CTCS-3级列控系统的综合能力模型,如图3所示。其中,六边形的面积S0、S分别表示CTCS-3级列控系统综合额定能力与系统完成规定功能能力的一次度量(即面积S0表示列控系统全模块正常运行,实现保证列车安全运行的同时完成记录采集等功能,面积S表示列控系统完成规定功能能力的一次实际度量)。选用S/S0作为综合指标,度量列控系统的可靠性。

图3 CTCS-3级列控系统的综合能力模型
列控系统上述六方面功能又分别依靠相应的设备来支撑。根据CTCS-3级列控系统的结构与功能,构建相应的功能层次结构模型,如图4所示。其中,A层为目标层,B层为中间层,C层为最底层。

图4 CTCS-3级列控系统硬件功能层次结构模型
3.1.2 可靠性评价云模型
根据S/S0的取值范围以及专家经验,将评价集划分为5个评价元素。即系统保持全部功能、保持主要功能、保持基本功能、保持最低功能、出现致命故障,各评价元素对应的综合指标取值范围及云表示见表2[20]。相应的可靠性评价云模型如图5所示,其中5个评价元素对应的含义见表3。

表2 评价集表示

表3 各评价元素对应的含义

图5 可靠性评价云模型
3.2 权重的确定3.2.1 层次分析法确定权重
利用层次分析法确定列控系统各底层设备的主观权重,由专家意见和9标度法构造的判断矩阵为
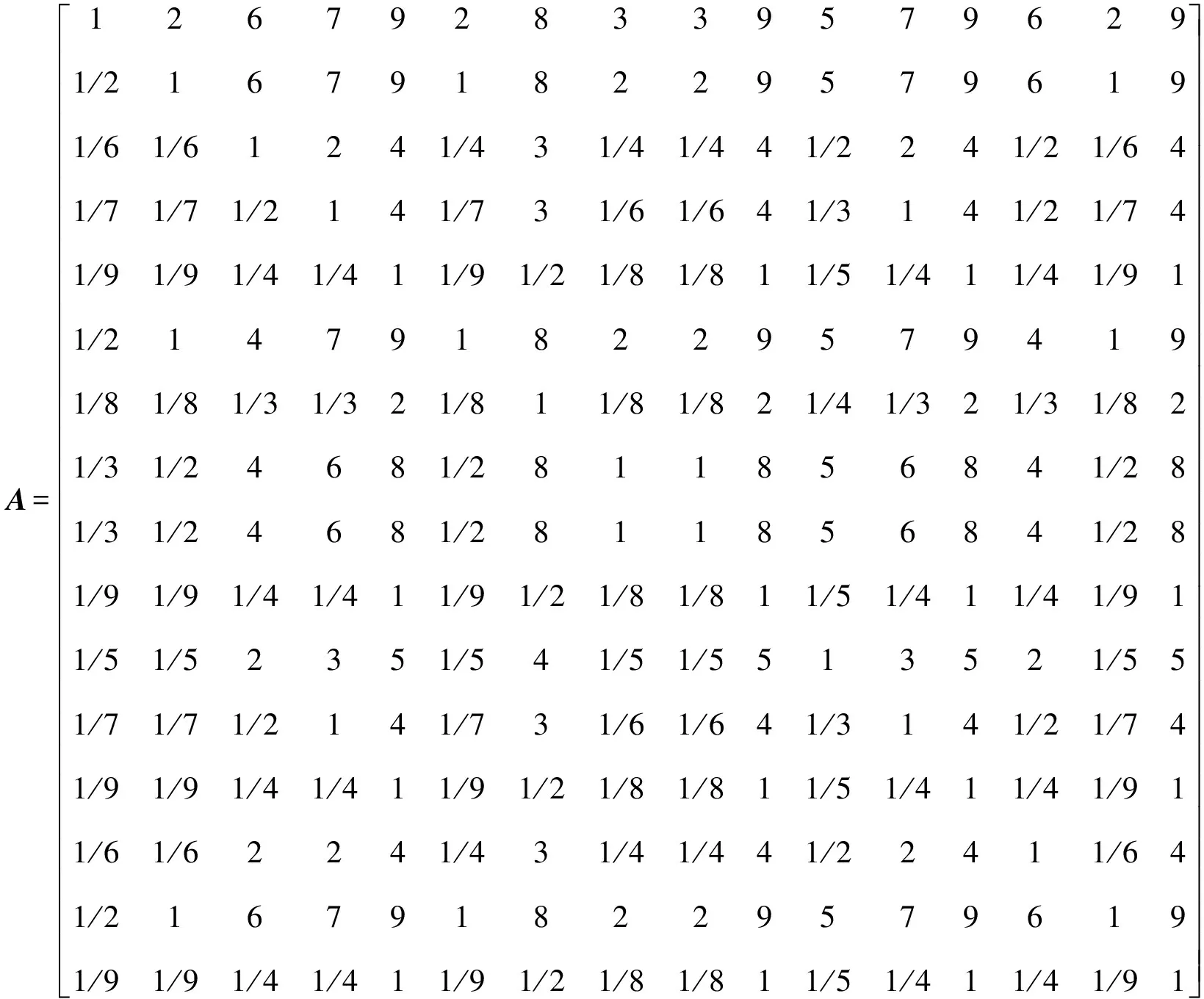
用MATLAB求出该判断矩阵A的最大特征根λmax及其相应的特征向量ω。对判断矩阵进行一致性检验:当一致性指标CI(Consistency Index)与随机一致性指标RI(Random Index)的比值,即随机一致性比率CR(Consistency Ratio)小于0.1时,认为判断矩阵具有一致性,否则必须调整该判断矩阵。
故该判断矩阵通过一致性检验。将ω进行归一化处理得到
WS=[0.178 898 0.138 041 0.031 622 0.024 900
0.010 371 0.130 265 0.014 409 0.099 495
0.099 495 0.010 371 0.043 955 0.024 900
0.010 371 0.034 496 0.138 041 0.010 371]
WS为CTCS-3级列控系统可靠性综合评价中16个底层单元的主观权重向量。
3.2.2 熵权法确定权重

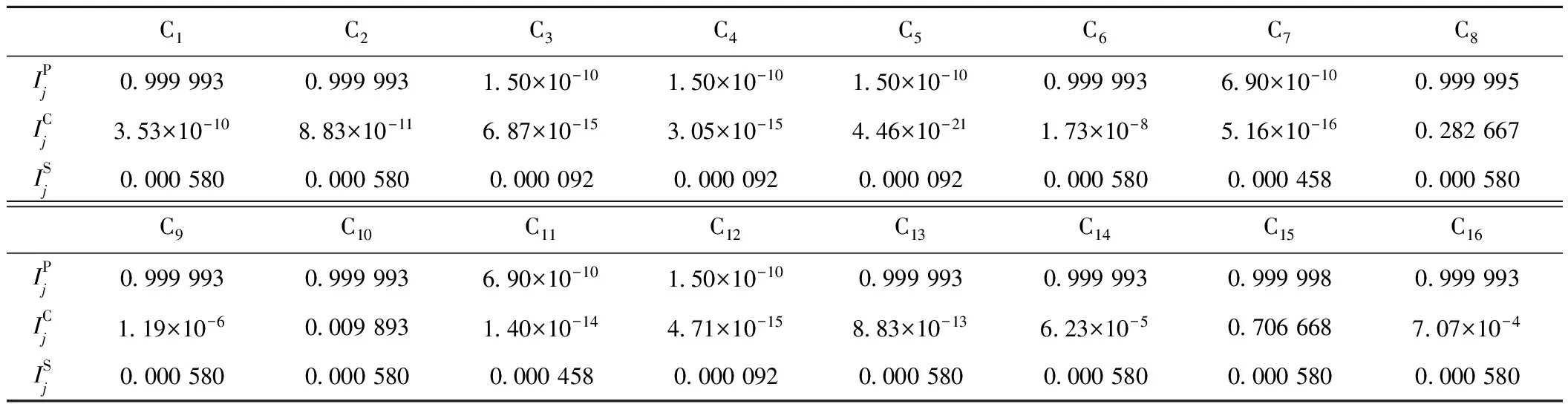
表4 CTCS-3级列控系统各单元的重要度
熵权法中特征比重的计算公式为
( 7 )
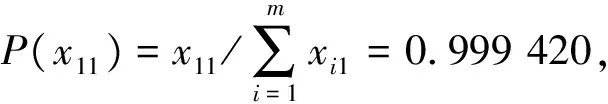
根据式( 2 )可以求得第j个单元的熵值ej。当m=3 时,k=(lnm)-1=(ln3)-1=0.910 2,依次计算出e1,e2,…,e16,得到
E=[0.004 460 0.004 460 0.000 022 0.000 022
0.000 022 0.004 460 0.000 020 0.483 387
0.004 467 0.054 513 0.000 020 0.000 022
0.004 460 0.005 065 0.619 961 0.009 760]
根据式( 3 )可以计算出相应的变异系数,得到
H=[0.995 540 0.995 540 0.999 978 0.999 978
0.999 978 0.995 540 0.999 980 0.516 613
0.995 524 0.945 487 0.999 980 0.999 978
0.995 540 0.994 935 0.380 039 0.990 238]
最后根据式( 4 )将H进行归一化处理,即可得到
WO=[0.067 244 0.067 244 0.067 544 0.067 544
0.067 544 0.067 244 0.067 544 0.034 895
0.067 243 0.063 863 0.067 544 0.067 544
0.067 244 0.067 203 0.025 670 0.066 886]
WO为CTCS-3级列控系统可靠性综合评价中16个底层单元的客观权重向量。
3.2.3 组合赋权法确定权重
首先将求得的主观权重向量WS的各个分量按从小到大的顺序依次排列,然后采用差异系数法求解综合赋权法联系的待定系数,根据式( 6 )计算得到:α=0.51,β=1-α=0.49。
最后根据式( 5 )即可求得CTCS-3级列控系统基本单元的综合权重相量W,计算结果见表5。
3.3 指标相对值的确定
假设基本单元的寿命t=5×104h,综合考虑系统冗余结构与共因失效对系统可靠性的影响,可以求得CTCS-3级列控系统基本单元的可靠度。考虑到系统失效过程中各种不确定性因素对系统可靠性的影响,本文采用三角模糊数描述各单元的模糊失效率,参照DUBOIS和PRADE提出的模糊数左右分布的确定原则,取与均值相差约为15%的值为其左右分布[20]。根据列控系统基本单元失效率的取值范围,可以得到相应可靠度的取值范围,CTCS-3级列控系统基本单元可靠性指标见表6。
结合表6中列控系统各个基本单元的可靠度取值范围,根据式( 1 )可以确定CTCS-3级列控系统基本单元实际指标与额定指标的比值,并采用云模型进行表示,见表7。
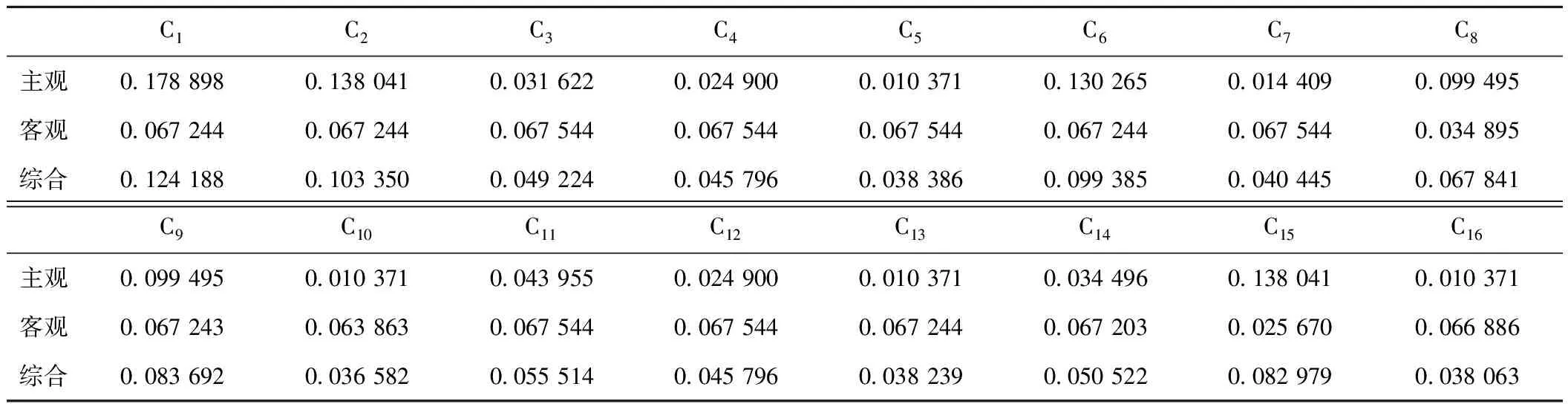
表5 CTCS-3级列控系统基本单元权重

表6 CTCS-3级列控系统基本单元的可靠性指标

续上表
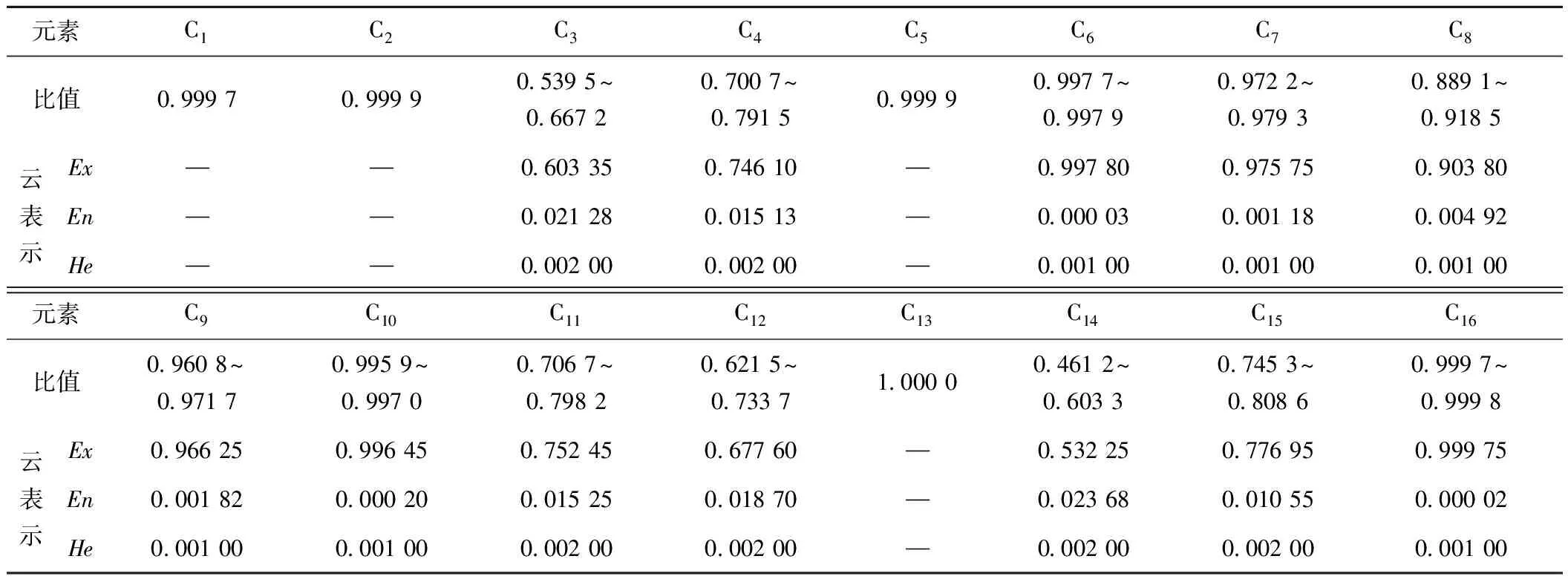
表7 CTCS-3级列控系统基本单元实际指标与额定指标的比值
3.4 列控系统可靠性评价结果
根据底层设备的权重值与指标相对值,可以得到CTCS-3级列控系统可靠性的综合指标云。求解过程中涉及到常数s与云C[Ex,En,He]的加法运算与乘法运算,以及云与云的加法运算。相应的运算规则为
s+C[Ex,En,He]=C[s+Ex,En,He]
( 8 )
s×C[Ex,En,He]=C[s×Ex,s×En,s×He]
( 9 )
C[Ex1,En1,He1]+C[Ex2,En2,He2]=
(10)
根据云运算规则可以求得
将列控系统可靠性综合指标云与相交的评价云作相似度度量,输出评价结果,如图6所示。其中黑色曲线表示CTCS-3级列控系统可靠性的综合指标云。

图6 评价云与综合指标云
由图6可知,列控系统可靠性的综合指标云与系统“保持全部功能”以及“保持主要功能”的评价云相交,根据文献[22]提出的基于期望曲线的正态云模型相似度计算方法,可以得出列控系统可靠性的综合指标云与“系统保持主要功能”的评价云更为相似。因此CTCS-3级列控系统可靠性的综合评价结果为“系统保持主要功能”,即系统性能良好,可以实现列控系统主要功能,防护列车安全运行。
4 结论
针对CTCS-3级列控系统的复杂性,建立科学的可靠性评价方法,对于列控系统的研发及评估具有重要的意义。为此,本文结合云模型和组合赋权法对CTCS-3级列控系统进行可靠性评价。
结合层次分析法与熵权法,使得列控系统中各单元权重的取值既能体现决策者的主观意愿又可以避免评价结果的主观随意性,为准确实现列控系统可靠性评价提供了有力的保障。采用云模型表示实际指标与额定指标的比值,使指标难以实测和量化的问题得以解决。利用云模型的特点和优势对列控系统进行可靠性评价,得到系统的可靠度等级,能够充分表征列控系统可靠度的模糊性和随机性,实现了定性与定量评价之间的转化,从而使可靠性评价结果更加客观准确。
参考文献:
[1]燕飞.列车运行控制系统安全保障与认证方法研究[J].中国安全科学学报,2010,20(12):98-104.
YAN Fei.Safety Assurance and Assessment Method Research for Train Control System[J].China Safety Science Joural,2010,20(12):98-104.
[2]廖武,张诤敏,孟祥春,等.云理论在作战飞机可靠性评估中的应用[J].计算机仿真,2005,22(7):235-238.
LIAO Wu,ZHANG Zhengmin,MENG Xiangchun,et al.Application of Cloud Theory in Reliability Assessment of Combat Aircraft[J].Computer Simulation,2005,22(7):235-238.
[3]张文韬,张友鹏,苏宏升,等.基于动态故障树的CTCS-3级ATP系统可靠性分析[J].工程设计学报,2014,21(1):18-26.
ZHANG Wentao,ZHANG Youpeng,SU Hongsheng,et al.Reliability Analysis on ATP System of CTCS-3 Based on Dynamic Fault Tree[J].Chinese Journal of Engineering Design,2014,21(1):18-26.
[4]邸丽清,袁湘鄂,王永年.CTCS-3级列控系统RAM指标评价方法研究[J].中国铁道科学,2010,31(6):92-97.
DI Liqing,YUAN Xiange,WANG Yongnian.Research on the Evaluation Method for the RAM Goals of CTCS-3[J].China Railway Science,2010,31(6):92-97.
[5]徐征捷,张友鹏,苏宏升.基于云模型的模糊综合评判法在风险评估中的应用[J].安全与环境学报,2014,14(2):69-72.
XU Zhengjie,ZHANG Youpeng,SU Hongsheng.Application of Risk Assessment on Fuzzy Comprehensive Evaluation Method Based on Cloud Model[J].Journal of Safety and Environment,2014,14(2):69-72.
[6]苏宏升,车玉龙,张友鹏.基于贝叶斯网络的CTCS-3级列控系统车载子系统可靠性评估[J].中国铁道科学,2014,35(5):96-104.
SU Hongsheng,CHE Yulong,ZHANG Youpeng.Dependability Assessment of CTCS-3 On-board Subsystem Based on Bayesian Network[J].China Railway Science,2014,35(5):96-104.
[7]罗一忠,吴爱祥,胡国斌,等.采场人-机-环境系统可靠性模糊综合评价[J].中南大学学报:自然科学版,2006,37(4):804-809.
LUO Yizhong,WU Aixiang,HU Guobin,et al.Reliability Fuzzy Comprehensive Evaluation of Man-machine-environment System in Stope[J].Journal of Central South University:Science and Technology,2006,37(4):804-809.
[8]陆刚,韩可琦,肖佳彬.矿井通风系统可靠性的模糊综合评价[J].采矿与安全工程学报,2008,25(2):244-247.
LU Gang,HAN Keqi,XIAO Jiabin.Fuzzy Integrated Evaluation for Reliability of Mine Ventilating System[J].Journal of Mining & Safety Engineering,2008,25(2):244-247.
[9]石剑飞,闫怀志.ARM嵌入式系统可靠性模糊综合评价方法[J].科技导报,2009,27(19):47-51.
SHI Jianfei,YAN Huaizhi.ARM Embedded System Reliability Fuzzy Comprehensive Evaluation Method[J].Science & Technology Review,2009,27(19):47-51.
[10]李德毅,于全,江光杰.C3I系统可靠性、抗毁性和抗干扰的统一评测[J].系统工程理论与实践,1997(3):23-28.
LI Deyi,YU Quan,JIANG Guangjie.A Unified Assessment of Reliability,Invulnerability and Anti-counterm Easurement for C3I Systems[J].Systems Engineering-theory &Practice,1997(3):23-28.
[11]张飞舟,范跃祖,孙先仿.基于云模型的导航系统模糊可靠性评测分析[J].自动化学报,2002,28(1):126-130.
ZHANG Feizhou,FAN Yuezu,SUN Xianfang.Assessment and Analysis of Fuzzy Reliability Based on Cloud Models in Aircraft Navigation System[J].Acta Automatica Sinica,2002,28(1):126-130.
[12]张飞舟,晏磊,范跃祖,等.基于云模型的车辆定位导航系统模糊评测研究[J].控制与决策,2002,17(5):550-553.
ZHANG Feizhou,YAN Lei,FAN Yuezu,et al.Fuzzy Assessment and Research of Vehicular Location and Navigation System Based on Cloud Models[J].Control and Decision,2002,17(5):550-553.
[13]何军旗,万少松,齐峰.基于云理论的导引头可靠性分析[J].战术导弹技术,2008(2):75-79.
HE Junqi,WAN Shaosong,QI Feng.Reliability Analysis of Seeker Based on Cloud Theory[J].Tactical Missile Technology,2008(2):75-79.
[14]李小静,刘立舰,刘林忠.基于云理论和雷达图的路网综合可靠度评价[J].计算机应用研究,2013,30(10):3 000-3 010.
LI Xiaojing,LIU Lijian,LIU Linzhong.Evaluation of Road Network Comprehensive Reliability Based on Cloud Theory and Radar Graph Model[J].Application Research of Computers,2013,30(10):3 000-3 010.
[15]李如琦,苏浩益.基于可拓云理论的电能质量综合评估模型[J].电力系统自动化,2012,36(1):66-70.
LI Ruqi,SU Haoyi.A Synthetic Power Quality Evaluation Model Based on Extension Cloud Theory[J].Automation of Electric Power Systems,2012,36(1):66-70.
[16]METIN D,IHSNA Y.Developing a Fuzzy Analytic Hierarchy Process(AHP) Model for Behavior-based Safety Management[J].Information Science,2008,178(6):1 717-1 733.
[17]ZOU Z H,YUN Y,SUN J N.Entropy Method for Determination of Weight of Evaluating Indicators in Fuzzy Synthetic Evaluation for Water Quality Assessment[J].Journal of Environmental Science,2006,18(5):1 020-1 023.
[18]庄万玉,凌丹,赵瑾,等.关于敏捷性评价指标权重的研究[J].电子科技大学学报,2006,35(6):985-988.
ZHUANG Wanyu,LING Dan,ZHAO Jin,et al.Research on Weights of Agility Appraisement Indexes[J].Journal of University of Electronic Science and Technology of China,2006,35(6):985-988.
[19]宁滨,唐涛,李开成,等.高速列车运行控制系统[M].北京:科学出版社,2012:106-138.
[20]覃庆努.复杂系统可靠性建模、分析和综合评价方法研究[D].北京:北京交通大学,2012:78-89.
[21]尹晓伟,钱文学,谢里阳.系统可靠性的贝叶斯网络评估方法[J].航空学报,2008,29(6):1 482-1 489.
YIN Xiaowei,QIAN Wenxue,XIE Liyang.A Method for System Reliability Assessment Based on Bayesian Networks[J].Acta Aeronautica et Astronautica Sinica,2008,29(6):1 482-1 489.
[22]李海林,郭崇慧,邱望仁.正态云模型相似度计算方法[J].电子学报,2011,39(11):2 561-2 566.
LI Hailin,GUO Chonghui,QIU Wangren.Similarity Measurement between Normal Cloud Models[J].Acta Electronica Sinica,2011,39(11):2 561-2 566.
