基于流固耦合的高速列车裙板支架气动载荷响应分析

张永昌，徐宇工，张乐乐

(北京交通大学 机械与电子控制工程学院，北京 100044)

高速列车车厢下部安装有设备舱，其两侧盖板被称为裙板[1]。目前已发现我国高速列车裙板与车身之间的连接支架出现开裂现象(如图1所示)，对列车行驶造成了极大的安全隐患。

结构断裂可分为过载断裂、疲劳断裂、蠕变断裂、应力腐蚀断裂等[2]。裙板支架裂纹的产生具有如下特点：在列车正常行驶过程中，裙板支架的应力远小于其静强度极限；裂纹是在列车运行一定里程后产生的；裙板支架没有显著的残余变形。根据上述特点判断该裂痕是结构疲劳造成的[3]。影响结构疲劳强度的因素有结构自身条件(几何外形、工件表面状态、材料本质等)及外界条件(工作环境、载荷条件等)[4]。本文针对裙板支架载荷条件进行研究。列车行驶过程中，裙板及支架受到的载荷可分为机械载荷和气动载荷，且气动载荷是主要的影响因素[5]。故本文重点研究裙板所受气动载荷的特点及其对裙板支架结构承载的影响。

图1 裙板支架裂痕

目前对列车所受气动载荷作用规律以及其承载特性的研究有实验及数值模拟两种。实验方面，通过实测得到结构应力较大位置的应变值，对其进行分析能够推算出结构所受载荷的大小[6]。该方法存在如下不足：只能监测有限个采集点的数据；无法区分气动载荷与机械载荷的作用规律；针对特定线路测试，适用范围有限。采用数值模拟的方法可以弥补上述不足。目前的数值模拟研究大致分为三种：在构件上施加人为假设的气动载荷进行求解[5]；对气动载荷进行求解，不分析构件的响应[7-9]；对气动载荷进行求解，然后将其施加于构件进行计算[10]。以上几种方法能够从一定程度上反映气动载荷下高速列车局部构件的响应问题，但都没有考虑流场与固体场的实时相互作用，描述不够准确。因此，有必要将流固耦合技术[11-14]引入针对高速列车局部构件所受气动载荷的作用方式和构件的结构响应的研究。另外，现有的列车空气动力学研究中，一般只研究列车外流场的流动情况[7-10，15]，而裙板所受气动载荷来源于裙板内外两侧流场的压力差，因此在考虑列车外流场的同时要对设备舱内流场进行研究，需要建立包含上述两部分流场的仿真模型。

本文讨论将流固耦合技术应用于高速列车局部构件结构承载分析的方法，建立包含列车外流场和设备舱内流场的仿真模型。以裙板支架的疲劳破坏问题为例，明确裙板所受气动载荷的产生原因及作用方式，进行裙板及支架的结构承载仿真，最终得到气动载荷对结构破坏的影响规律。

1 流固耦合仿真流程

流固耦合算法分为强耦合法和弱耦合法。其中，强耦合法对流场与固体场控制方程进行联合求解，不仅增加了求解难度，而且难以利用现有的CFD和CSD技术，因此在工程实际中应用较少。弱耦合法分别求解两个物理场，并且将两个物理场的物理信息进行交换从而实现耦合，应用较为普遍。弱耦合法又分为单向耦合法和双向耦合法，单向耦合法仅考虑流场对固体场的作用，双向耦合法同时考虑流场和固体场的相互作用。

本文基于ANSYS workbench平台，采用双向弱耦合法，流体部分通过计算流体动力学软件CFX进行求解，固体部分通过瞬态有限元分析模块Transient Structural进行求解。计算过程中依次对流场与固体场的控制方程进行求解，这些控制方程由质量守恒定律、动量守恒定律等导出。实现耦合求解的方法为：在流固交界面上交换流体控制方程和固体控制方程的求解数据。交换过程遵循以下原则：在流固交界面上，流体与固体的作用力、位移等变量相等。由于CFD计算与CSD计算使用的网格不同，流体与固体网格节点很难重合，在传递节点力时利用映射算子先将流体节点应力映射到固体节点，然后通过积分求出固体节点力。另外，固体位移会导致计算域变形，采用ALE方法描述网格节点的运动，并应用修正的弹性方程对网格进行更新[16]。

对于本文所研究的具体问题，其求解流程如图2所示。分别建立流场及固体场仿真模型，在两者的交界面建立流固耦合面。流场与固体场分别求解，在求解时数据传递过程为：在流固耦合面，通过差值将流场计算所得气动载荷数据传递到裙板内外表面的固体场网格，固体场计算得到的裙板产生的位移、形变数据传递到流场网格。最后，分析气动载荷以及结构承载的特性，得到前者对后者的影响规律。

图2 流固耦合仿真流程

为了保证耦合的准确性，本文对流场及固体场求解进行了统一的时间和空间控制。时间控制方面，两者采用相同的求解时长和时间步长。每个时间步内，流场与固体场求解器进行数据传递，传递过程进行多次迭代。每个数据传递迭代步内，流场与固体场分别进行求解，两者的求解器分别进行迭代计算。反复迭代直至收敛，然后进入下一时间步。空间控制方面，流场与固体场采用统一的坐标系，保证两者相对位置相同，并在两者交界面(即裙板内外表面)处采用相近的网格尺寸，从而降低数据传递过程中可能产生的误差。

2 仿真模型的建立

本文所建立的流固耦合仿真模型如图3所示，该模型分为固体场及流场两部分。

图3 流固耦合仿真模型

2.1 固体场模型

固体场模型包括列车、设备舱、裙板及支架模型。其中，列车、设备舱模型用于为流场模型划定壁面边界，裙板及支架模型用于结构动载荷计算。实际列车结构十分复杂，需要进行简化，忽略固体场对流场影响较小的结构。

(1)列车模型

如图3(a)所示，由于列车中间部分截面不变，缩短的模型对列车流场结构改变较小[17]，本文采用3节车编组的CRH3型高速列车，全车长76 m。去掉车身的细小结构以及复杂的转向架结构。

(2)设备舱模型

为了模拟设备舱内部的流场，需要建立车下设备舱模型。为简化计算，只在中间车底部建立设备舱舱体。如图3(b)所示，舱体由裙板等构成，其两侧布置有4个尺寸为670 mm×510 mm四边形通风口。车下设备简化为规则六面体。

(3)裙板及其支架模型

以列车后部某裙板为例，其结构如图3(c)所示。裙板厚6 mm，通过三个裙板支架与车体相连。所有固体均采用线弹性材料模型以及铝合金材料，其密度为2 770 kg/m3，杨氏模量为71 GPa，泊松比为0.33。由于支架后端固定于车体且裙板下端与设备舱底板相互连接，故支架后端和裙板下端为固定约束。裙板内外表面为流固耦合面，用以接收气动载荷数据，同时将固体位移数据传递至流体求解器。结构网格如图4所示，其中裙板网格尺寸为20 mm，支架网格尺寸为3 mm。

图4 裙板及支架网格

2.2 流场模型

流场模型包括车外流场及设备舱内流场，两者通过设备舱通风口相连。车外流场模型尺寸如图3(d)所示。

使用结构化网格划分方式，在流动复杂的区域，如车头、车尾以及设备舱附近进行加密。在车体表面、设备舱内外表面及地面处生成边界层网格，为配合壁面函数的使用，设置边界层网格的无量纲厚度y+>30。最小网格尺寸为50 mm，网格数量为445万，网格无关性验证见2.3节。列车表面网格见图5。

图5 列车表面网格

采用高精度差分格式对控制方程进行离散。由于马赫数小于0.3，按不可压缩流动处理。由于仿真同时涉及远离壁面的车外流场以及靠近壁面的设备舱内流场，本文采用在这两种区域都有良好适应性的SST湍流模型。在近壁面区域使用标准壁面函数。

边界条件的设置如图3(d)所示：计算域前端为速度入口，入口速度为列车行驶速度；后端为压力出口，压力取101 325 Pa；顶端及两侧为对称边界；车身外表面以及设备舱内各种结构均为壁面边界；地面为移动壁面边界，以来流速度移动，从而模拟地面气动效应。裙板内外表面为流固耦合面，其表面网格节点的位置由固体计算所得位移数据确定。由于裙板变形较小，故无需进行大范围的网格重构，仅改变裙板附近网格的位置，节点位移值由式( 1 )确定。

( 1 )

式中：δ为网格节点的位移值；Vc为网格体积；Cs为常数。

一般认为，若数值模型的库朗数(uΔt/Δx，其中，u为空气流速；Δt为时间步长；Δx为网格尺寸)小于1，则计算收敛性较好。本文选取时间步长为4×10-4s，对于不同的车速，模型的库朗数为0.56～0.85，满足收敛性要求。同时，这一时间步长也远远小于本文所涉及的压力波动周期，满足数据采样的要求。

2.3 模型的验证

2011年，针对高速列车裙板支架疲劳开裂的问题，文献[5]通过长距离(1 200万km)线路运行测试得到了设备舱支架不同位置的受力情况。

根据实测结果，当列车以380 km/h的速度明线行驶时，裙板两侧气压差为496 Pa，筋板与L形板连接部位焊缝角端受到较大的应力，其最大值为26.1 MPa。

本文分别以不同网格尺寸对计算域进行网格划分。不同网格计算结果与实验结果的对比见表1。可以看出，使用网格2与网格3所得的仿真结果与实测结果之间的相对误差均可控制在5%以内，故选择计算成本较低的网格2进行后续仿真分析。

表1 仿真结果与实验结果对比

3 流场特性分析

车外流场及设备舱内流场共同决定了裙板所受气动载荷的特性。以车速为300 km/h的明线、无交会、匀速直线行驶工况为例，分析两部分流场以及气动载荷的特点。

3.1 列车外流场分析

图6为用等压面表示的列车行驶过程中车身周围的流场结构。在0.1 s时刻，位于尾车右侧的等压面A面积较大，而其左侧的等压面C面积较小且位置更靠近尾车前部。另外，中间车左侧的等压面B位于中间车的中部，该处正是设备舱通风口1所在位置。在0.35 s时刻，等压面A面积变小，等压面C面积增大且更靠近尾车后部，而等压面B则移至中间车的后部。0.6 s时刻等压面的分布类似于0.1 s时刻，而0.85 s时刻又与0.35 s时类似。由此可见，在考虑设备舱内流场流动情况之后，仿真模型能够体现列车周围流场结构的变化。这种变化具有周期性，是交变气动载荷产生的原因。

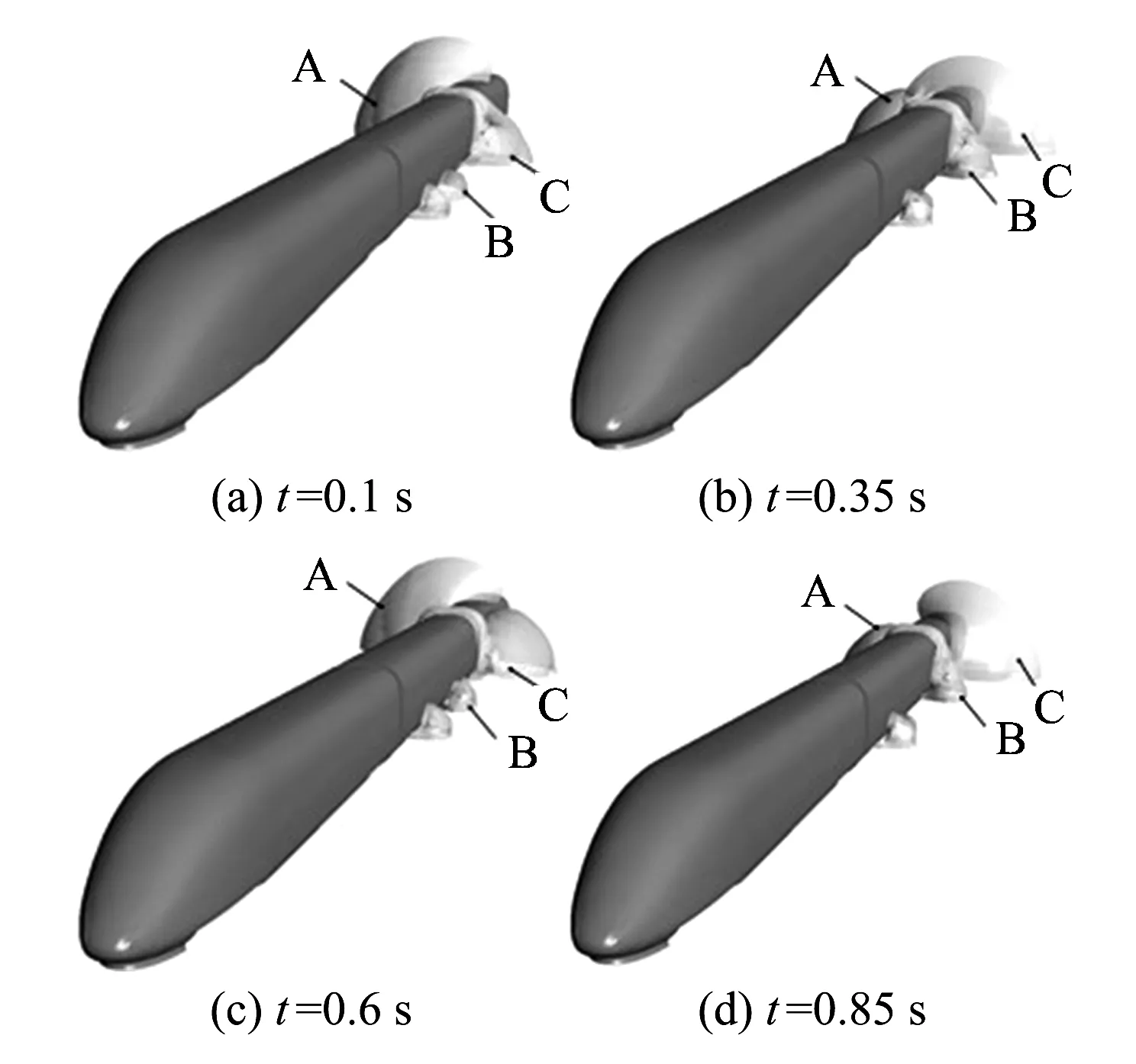
图6 外流场结构变化(等压面P=-50 Pa)

如图7所示，为了说明不同位置处压力变化情况，在设备舱内外分别设置9个观察点。

图7 观察点位置

舱外观察点1～6的压力时程曲线如图8所示。尽管列车以某一速度稳定运行，但由于列车周围流场结构进行周期性变化，各观察点的压力随时间均作正弦变化。其变化幅值与相位不同，而周期均相差很小。定义流场中同一位置压力最大值与最小值的差为压力变化幅值。以设备舱前端为原点，舱外压力变化幅值沿车长方向的变化如图9所示。可见，设备舱前端舱外压力变化较小，而后端较大。由于受到转向架处复杂扰动的影响，在14 m位置处压力变化有所降低。从总体看，设备舱后部的裙板受到气动载荷的变化较为剧烈。

图8 设备舱外观察点压力变化曲线

图9 压力变化幅值在车长方向的变化(列车左侧)

3.2 设备舱内流场分析

以图10所示的流动矢量图来说明设备舱内流场结构的变化。设备舱前部的流体流动缓慢，同时流动变化较小。而其后部流动情况复杂，流体在尾部空腔内形成漩涡。漩涡与裙板之间流体的流动方向作周期性变化：在0.25 s时刻，设备舱左后侧流体产生一定的横向流动；0.25 s之后，横向流动减少；而在0.75 s时刻，这种横向流动再次出现，且方向与0.25 s时刻相同；随后，横向流动再次减少。

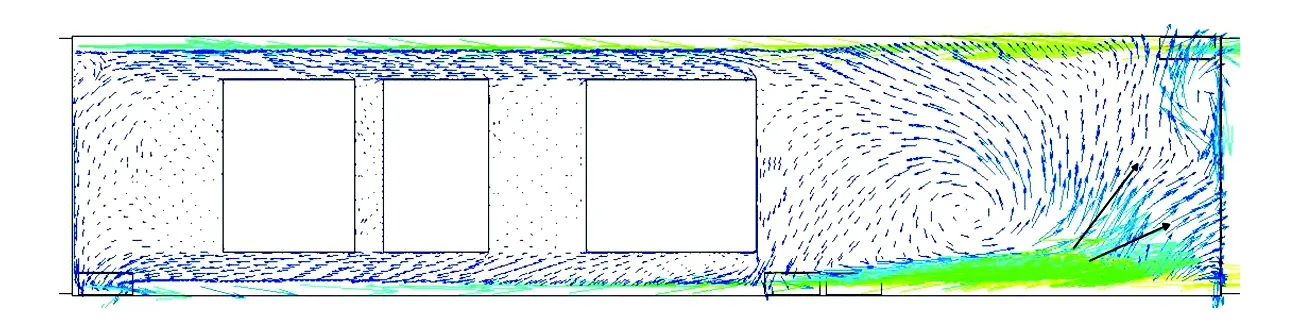
(a)t=0.25 s

(b)t=0.5 s

(c)t=0.75 s

(d)t=1.0 s图10 设备舱内流动速度矢量图

如图11所示，设备舱内观察点7～9(图7)的压力同样呈现出正弦变化。值得注意的是，在这种工况下，设备舱内的流场结构变化周期与车外流场变化周期基本相同。与舱外不同的是，舱内各观察点的压力变化幅值小，且不同位置幅值相差较小。

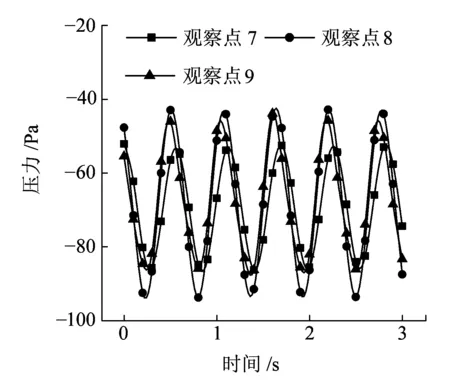
图11 设备舱内观察点压力变化曲线

3.3 裙板气动载荷分析

裙板两侧流场的压差为裙板气动载荷的来源。图12为设备舱四个拐角处裙板中心处压力差的时程曲线。可见，气动载荷同样呈正弦变化。图13显示了各裙板中心处的最大压力差。沿车长方向对列车左右两侧裙板进行编号，编号越大越靠近设备舱后端。可以看出气动载荷呈现出后部大于前部，右侧大于左侧的分布趋势。造成这种现象的原因在于靠近车身后方的流场变化更加剧烈，而不对称的通风口布置造成列车左右两侧气动载荷具有一定差异。

图12 压力差变化曲线

图13 裙板中心最大压力差

3.4 车速对流场特性的影响

本文计算了不同列车行驶速度的多种工况。以受较剧烈气动载荷作用的图3(c)中所示裙板为研究对象，考察其中心处压力差与车速的关系。图14为该裙板中心两侧的最大压力差以及压力差变化频率随列车行驶速度变化的曲线。可见，最大压力差及变化频率均随车速的提升而增加，其中最大压力差增加明显而变化频率增幅很小。

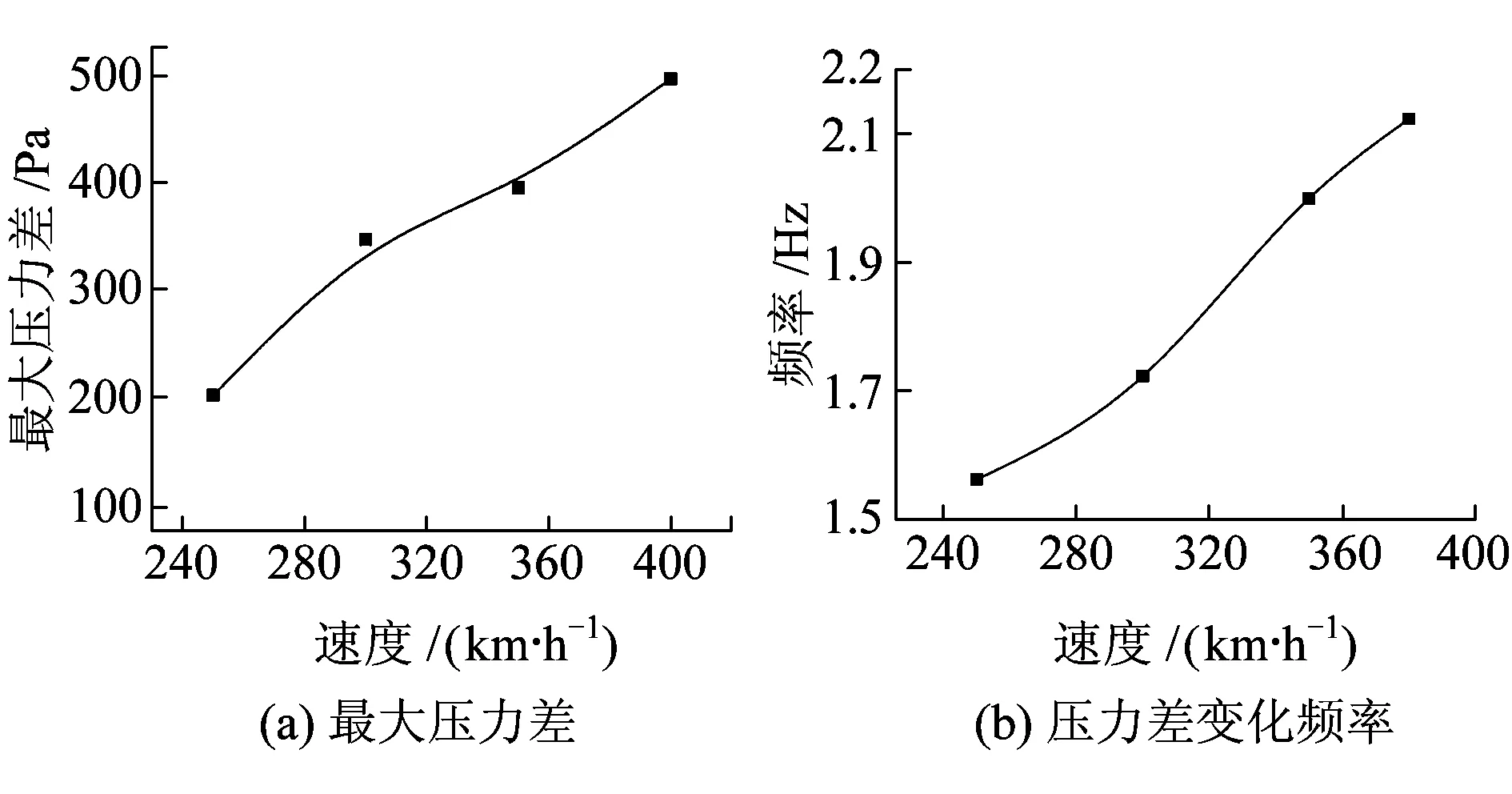
图14 车速对气动载荷的影响

4 裙板支架的动载荷响应

在复杂的气动载荷作用下，列车裙板在设备舱内外压力差的作用下产生形变，这些形变由连接结构传递至裙板支架，从而导致支架局部位置产生应力集中。同时，由于气动载荷的交变特性，应力集中区域易产生疲劳破坏现象，影响其使用寿命。

4.1 气动载荷作用下裙板的变形

车速为300 km/h情况下，图3(c)中所示裙板的位移情况如图15所示。由于该裙板的固定支架位置偏左，故其右端位移较大，左端位移较小，产生扭曲，对支架承载造成影响。

图15 裙板位移云图(外侧)

以该裙板中心处为观察点，其压力差及各向(其中x方向为车长方向，y方向为车厢高度方向，z方向为车厢宽度方向)位移曲线如图16所示。其中，压力与各方向位移的变化规律基本相同，压力变化的幅值与频率直接决定裙板位移变化的幅值与频率。而裙板在y、z方向的位移值明显大于x方向，说明y、z方向的交变位移是造成裙板支架疲劳破坏的主要因素。

图16 裙板中心压力差及位移变化曲线

4.2 裙板支架的动应力特征

裙板由于气动载荷作用产生的位移传递至裙板支架，在裙板支架的某些区域产生高应力。计算结果表明，裙板支架的最大应力值出现在筋板连接处，与实际开裂位置(图1)相同。

由图17可知，裙板支架筋板连接处应力在一定范围内呈周期变化。在这种交变应力的作用下，筋板连接处容易产生疲劳裂纹，进而产生断裂现象。

图17 裙板支架筋板连接处应力变化曲线

4.3 车速对动应力的影响

由图18可知，随着列车行驶速度的增加，裙板支架筋板连接处的最大应力逐渐增大，这将导致结构更容易产生疲劳破坏。

图18 车速对裙板支架应力的影响

4.4 裙板支架破坏机理的讨论

以列车车速为300 km/h的工况为例。为了考察气动载荷与机械载荷的耦合作用机理，分别对裙板及支架施加气动载荷、机械载荷以及同时施加气动载荷及机械载荷组成的耦合载荷。

气动载荷的加载由上述流固耦合模型完成。对于机械载荷，本文假定在列车行驶过程中，裙板及支架受呈正弦变化的振幅为1.4g、频率为2 Hz的垂向振动加速度。

图19为三种载荷下，同一裙板支架筋板连接处的应力变化时程曲线。可见，三种载荷工况下，结构应力均呈周期性变化。与气动载荷相比，机械载荷作用下结构应力较小。在耦合载荷作用下，结构的响应更为复杂，与气动载荷与机械载荷下应力的线性叠加结果有明显差异，在某些时间段内结构应力值有所降低。

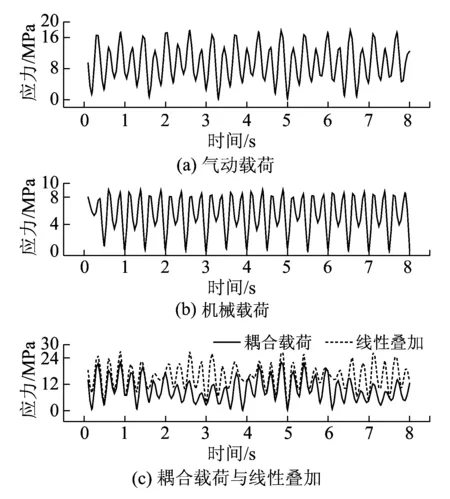
图19 不同载荷作用下结构应力时域对比

如图20所示，通过频域分析可知，气动载荷作用下，结构应力最大频率为3.5 Hz，而机械载荷为4 Hz。两者耦合则会造成应力频域特性的改变。耦合载荷作用下，应力幅值的频率主要集中于气动载荷起主导作用的3.5 Hz以及两种载荷之间的3.75 Hz。

图20 不同载荷作用下结构应力频域对比

5 结论

对明线行驶过程中列车裙板支架疲劳破坏问题进行了流固耦合仿真分析。得到如下结论：

(1)导致裙板支架产生疲劳破坏的主要原因为：列车行驶过程中车身周围及设备舱内流场结构发生周期性变化，造成设备舱内外压力差发生周期变化，从而使裙板受到周期性气动载荷的作用。

(2)气动载荷具有如下特征：靠近列车后部裙板所受气动载荷幅值较大，而所有裙板所受气动载荷频率基本相同；随着列车行驶速度的增加，气动载荷幅值明显增加，而频率增加幅度较小。

(3)在气动载荷作用下，裙板在列车高度及宽度方向的交变位移是造成裙板支架疲劳破坏的主要原因。裙板支架筋板连接处出现应力集中，该位置应力小于其材料的屈服强度，但呈现周期性变化，易造成疲劳破坏。气动载荷与机械载荷的耦合作用比较复杂，耦合载荷作用下结构响应的时域特性与频域特性与两种载荷分别作用以及两者线性组合作用下均不相同，有待进一步深入研究。

参考文献：

[1]杜秋男,李瑞淳.高速动车组裙板设计研究[J].铁道车辆,2008,46(6):8-13.

DU Qiunan,LI Ruichun.Design Research of Skirt Board of High-speed Train[J].Rolling Stock,2008,46(6):8-13.

[2]张骁勇.材料的断裂与控制[M].西安：西北工业大学出版社,2012:30-31.

[3]熊峻江.疲劳断裂可靠性工程学[M].北京：国防工业出版社,2008:4-5.

[4]殷之平.结构疲劳与断裂[M].西安：西北工业大学出版社,2012:28-32.

[5]佟胜江.设备舱支架裂纹原因分析及改进措施[J].铁道车辆,2011,49(12):10-14.

TONG Shengjiang.Crack Cause Analysis of Equipment Cabin Supports and Improvement Measure[J].Rolling Stock,2011,49(12):10-14.

[6]李振平.CRH3动车组裙板支座载荷识别及疲劳寿命评估[D].北京：北京交通大学,2010.

[7]李人宪,赵晶,刘杰,等.高速列车会车压力波对侧窗的影响[J].机械工程学报,2010,46(4):87-98.

LI Renxian,ZHAO Jing,LIU Jie,et al.Influence of Air Pressure Pulse on Side Windows of High-speed Trains Passing Each Other[J].Journal of Mechanical Engineering,2010,46(4):87-98.

[8]张军海.基于FLUEN丁的高速机车气动刮雨器数值模拟研究[D].成都:西南交通大学,2010.

[9]郭迪龙,姚拴宝,刘晨辉,等.高速列车受电弓非定常气动特性研究[J].铁道学报,2012,34(11):16-21.

GUO Dilong,YAO Shuanbao,LIU Chenhui,et al.Unsteady Aerodynamic Characteristics of High-speed Pantograph[J].Journal of the China Railway Society,2012,34(11):16-21.

[10]龚晓波.动车组自动开闭装置空气动力效应与结构强度分析[D].长沙:中南大学,2010.

[11]ZILIAN A,DINKLER D,VEHRE A.Projection-based Reduction of Fluid-structure Interaction Systems Using Monolithic Space-time Modes[J].Computer Methods in Applied Mechanics and Engineering,2009(198):3 795-3 805.

[12]SOARES D.Fluid-structure Interaction Analysis by Optimised Boundary Element-finite Element Coupling Procedures[J].Journal of Sound and Vibration,2009(322):184-195.

[13]BRUMMELEN E H V.Partitioned Iterative Solution Methods for Fluid-structure Interaction[J].International Journal for Numerical Methods in Fluids,2011(65):3-27.

[14]OSTASEVICIUS V,DAUKSEVICIUSA R,GAIDYS R,et al.Numerical Analysis of Fluid-structure Interaction Effects on Vibrations of Cantilever Microstructure[J].Journal of Sound and Vibration,2007(308):660-673.

[15]田红旗.列车空气动力学[M].北京:中国铁道出版社,2007.

[16]钱若军,董石麟,袁行飞.流固耦合理论研究进展[J].空间结构,2008,14(1):3-15.

QIAN Ruojun,DONG Shilin,YUAN Xingfei.Advances in Research on Fluid-structure Interaction Theory[J].Spatial Structures,2008,14(1):3-15.

[17]黄志祥,陈立,蒋科林.高速列车模型编组长度和风挡结构对气动阻力的影响[J].实验流体力学,2012,26(5):36-41.

HUANG Zhixiang,CHEN Li,JIANG Kelin.Influence of Length of Train Formation and Vestibule Diaphragm Structure on Aerodynamic Drag of High Speed Train Model[J].Journal of Experiments in Fluid Mechanics,2012,26(5):36-41.