紧急情况下城市轨道隧道客流疏散配流模型研究

马 剑，王若成，邱谦谦

(1.西南交通大学 交通运输与物流学院，四川 成都 610031；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031)

随着我国城市轨道建设不断扩增，城市轨道隧道里程逐年攀升。在隧道里程不断增加的同时，隧道安全问题也越发值得关注。由于隧道构造特殊，一旦发生火灾，烟气和热量在隧道内部大量积聚，人员疏散及应急救援工作不易展开。因此，如果缺乏有效的疏散救援方案，极易引起重大人员伤亡和严重财产损失。

目前，国内外研究人员针对隧道疏散开展了一系列研究工作。由于隧道火灾危险性大，烟气和热量容易积聚，因此，列车在隧道内遭遇火灾时的一个基本的处置原则是驶离隧道后到达车站再进行应急处置与人员疏散[1]。但是，受不确定性影响，紧急情况下列车停驶在隧道内的情况时有发生。例如，最近北京、纽约、上海三地的事故中列车均在隧道内停止运行[2-4]。因此隧道内列车疏散的研究引起了广泛的关注。文献[5，6]选择100名实验对象在隧道内进行仿真疏散，研究隧道疏散过程中人员的路径、速度选择与行为表现，而后又建立隧道列车疏散模型，研究不同类型的车门对人员疏散效率的影响。文献[7]对列车中部发生火灾的人员逃生进行了研究，提出保证人员疏散安全的联络通道间距。文献[8]根据计算机模型建立了人员疏散数学模型，得出高海拔特长隧道内人员安全疏散的必需时间，提出了确保安全疏散的隧道防排烟设计参数。文献[9]模拟火灾发生时烟气特性对人员疏散的影响，提出了城际轨道隧道防灾系统设计方案。文献[10]通过建立隧道人员疏散模型，提出了基于安全疏散的隧道建设方案。文献[11]基于 M/G/c/c 模型，结合地铁车站楼梯通道疏散能力，分析了地铁车站楼梯通道疏散瓶颈。文献[12]分析地铁车站出口布局变化对人群疏散性能的影响程度等。文献[13]以CRH1型动车组列车在狮子洋隧道被迫在最不利情况停车时的人员疏散为例，评估了救援通道宽度、横通道入口宽度以及横通道间距设置的合理性。文献[14]提出了基于预案综合评价模型、计算机数值模拟计算和动态仿真的地铁火灾应急预案性能化设计方法。

隧道客流疏散过程中，人员的安全性较大程度上取决疏散的效率，组织有序的疏散可以减少总的疏散时间，从而有效避免大规模人员伤亡。然而，目前尚缺乏有效的隧道客流疏散组织模型。基于此，为提高城市轨道隧道疏散安全性，本文考虑列车车门与隧道横向通道通行能力的限制条件，结合隧道疏散的结构特征，将隧道疏散空间划分成不同分区，继而构建车门到可能疏散联络通道的疏散网络，在各区域待疏散人数给定的条件下，以疏散时间最短为目标函数，求解不同情境下的人员疏散配流方案。

1 隧道客流疏散方式分析

当列车在隧道中停驶时，旅客可以经由车门疏散至隧道中，再经联络通道疏散至安全区。目前，我国GB 50157—2003《地铁设计规范》要求两条单线区间隧道之间，当隧道连贯长度大于600 m时，应设置联络通道[15]。联络通道的设置使得疏散过程成为如图1所示的典型多出口疏散过程。这一疏散过程可分为三个阶段：初始位置到车门Ⅰ、车门到横向联络通道端部Ⅱ、联络通道端部到相邻隧道Ⅲ。

图1 隧道旅客疏散三阶段示意图

在第Ⅰ阶段，由于车厢内乘客距离车门较近，人员密度高，步行速度几乎不影响疏散时间，因而乘客由其初始位置行进至车门的运动时间只与车门通行能力有关[16]。而在经由疏散平台到达联络通道端部的第Ⅱ阶段，乘客的行进时间则包括行人运动时间，以及由于联络通道通行能力限制而导致人员排队等待的附加时间。在这一阶段如无合理人员疏散组织方案，极易形成相向行人流和交叉行人流，影响疏散速度，且拥挤过程极易造成踩踏等二次事故[17]。乘客到达横向联络通道端部后，仅需沿着联络通道到达安全位置，这一阶段持续时间长短仅与人的步行速度有关。综上分析，客流疏散的第Ⅱ阶段是影响疏散时间的重要因素。

乘客从车门经由疏散平台运动至联络通道端部的时间由无阻碍时的人员自由运动时间ts与联络通道拥堵而形成的附加等待时间tw共同组成，即tc-t=ts+tw。考虑到疏散过程中的拥堵并不是固定在某一空间位置上，而是随时间动态演变，因此，由联络通道拥堵所产生的等待时间可以转化为疏散人员缓速运动问题。研究表明，行人运动速度的大小取决于冲突点的大小、数目多少以及距离远近[17]，换言之，乘客运动速度与拥堵率有关。

为模拟如前所述的隧道内乘客疏散特征，可采用分区的方式将乘客由车门至横向联络通道端部的疏散平台划分为不同区间，将车门通行能力作为单位时间内进入疏散平台乘客数目的约束条件，通过疏散平台各区间内实时拥堵率求解乘客在该区间内的运动速度，根据各区间面积的大小及速度差异获取区间内乘客运动时间，最终获得乘客从车门通过分区到达联络通道端部的时间，也即乘客疏散时间。

2 基本模型参数

2.1 问题描述

以G=(A，B，C)表示乘客疏散网络，其中，A={ai|i=1，2，…，m}表示疏散场景中所有车门ai构成的源节点集合；B={bj|j=1，2，…，n}代表由不同联络通道bj构成的汇节点集合；C={cx|x=1，2，3，…，v}代表车门到联络通道路段分区的路段集合。以车辆运行方向为车头，依次向车尾编号，共有m个车门，n个联络通道，v个路径。相应地，每个分区最大可容纳人员个数的集合记为S={sx|x=1，2，3，…，v}，分区行人运动距离的集合记为D={dx|x=1，2，3，…，v}。

2.2 分区的确定

行人运动速度的大小，受到运动区间内障碍物数量及类型(固定、相向、同向)的影响。不同运动方向的行人交叉运动时存在自组织现象及分层现象[17]，因而，有速度夹角的区域应该着重单独考虑。对于行人从车门运动至联络通道端部的疏散平台上，速度方向夹角明显的是联络通道端部口与车门，因而，在区间划分中，采取将车厢部分的车体对应的疏散平台区间、车门部分对应的疏散平台区间、联络通道至行人可运动极限空间分别划分为不同分区。典型的分区划分如图2所示，其中，Δh表示联络通道间距，Δx表示车体与隧道间距，L表示两车门间的间隔，l表示车门宽度，H为联络通道宽度。

图2 隧道疏散分区方法示意图

2.3 拥挤度及对应速度

( 1 )

( 2 )

3 客流疏散配流模型构建

3.1 条件假设

考虑前文分析的疏散过程的特征，建立如下基本假设：

(1)行人从车门出来第一个的分区的行人运动距离近似看作车门中心到分区宽度中心直线间距，联络通道处行人运动距离近似看作联络通道端中心到分区宽度中心的直线间距，其他分区行人运动距离即为分区长度。

(2)疏散完成时间即为最后一位乘员到达联络通道端部的时间。

(3)每位乘客都具有自主疏散能力，其行人特性及最大运动速度以25岁正常男子计。

(4)行人在各分区内的运动速度以进入该分区时的平均速度计算。

3.2 人员疏散模型

隧道疏散所涉及的人员疏散仿真模型，整体过程为人员从车门走出开始，行人沿着联络通道端部所在方向，不断通过各个分区，最终到达联络通道端部，即为其完成疏散过程。t时刻分区x的拥挤度为

( 3 )

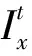
若t时刻行人进入分区x拥挤度大于1，则不允许距通道较远的行人进入分区，直到分区内有人离开。t时刻分区内行人运动速度可由式( 2 )确定，行人k在区间cx内的运动时间为

( 4 )

那么，行人从车门出来到达联络通道端部的总时间为

( 5 )

3.3 配流模型

疏散过程中，人员往往选择离自己最近的出口，因此，选择所有人经由最短路径疏散作为模型的初值。确定上述参数后，客流分配主要基于以下四个步骤完成：

步骤1确定模型基本参数(各车门待疏散人数及人员疏散路径选择情况)。

步骤2模拟行人运动，确定每个人员的疏散完成时间、联络通道疏散完成时间、疏散总的完成时间，具体的计算如下：

模型中，每个人的疏散完成时间为其从车门出来的时间加上在路径中运行的时间，即

( 6 )

疏散完成时间是最后一个人到达联络通道的时间，表示为

( 7 )

式中：Tf为疏散完成时间；λ(i，j)为第i个车门经由第j个联络通道疏散的总人数。

每个联络通道的疏散完成时间为经由该通道疏散的所有人中最后一个到达的时间点，即

( 8 )

式中：tBj为联络通道bj的疏散完成时间。

最早完成疏散的联络通道为疏散完成时间最短的联络通道，最晚完成疏散的联络通道为疏散完成时间最长的联络通道。

( 9 )

(10)

式中：tBf表示最快完成疏散的联络通道的总疏散时间，取该值的联络通道编号记为Sf；tBl表示最晚完成疏散的联络通道的总疏散时间，取该值的联络通道编号记为Sl。

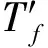
(11)

被调整人员所在车门满足在所有经疏散时间最长的联络通道疏散的车门中距该相邻通道最近，该距离为sLc，取得sLc的车门编号记为sTc，sLij为车门ai到联络通道bj的距离。

sLc=min{sLij|j=Sc，xij≠0}

(12)

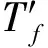
综上，紧急情况下的隧道疏散配流模型流程图如图3所示。

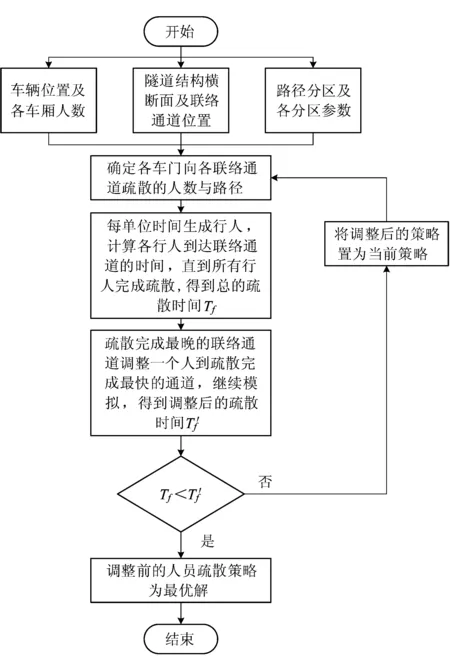
图3 配流模型流程图

4 案例分析与讨论

通过前文的分析可以发现，联络通道间距、疏散平台宽度、列车编组辆数、停车位置等因素都会影响隧道内客流疏散过程。本文以某在建城市轨道隧道为例，研究配流方案对疏散效率的影响。该隧道设计横向联络通道间距150 m、列车右端距右端联络通道25.77 m、车门间距4.62 m、每节车厢长18.61 m，假设列车与隧道间纵向疏散平台宽度为0.6 m、0.8 m与1.0 m，在这三种情况下分别计算不同的客流实时最优配流方案，并结合人员疏散模拟仿真软件Anylogic进行人员运动过程模拟计算，最终确定客流疏散时间。模拟计算中，假设列车具有4节车厢，12个车门，假定待疏散人数共360人，分别以人员均衡分布(每车门各疏散30人)、人员不均衡分布(车门待疏散人数从左到右为首项8、公差4的等差数列)作为模拟仿真初值，对比分析以下两种典型情形：

(1)没有做优化处理，所有乘员选择离自己最近的疏散通道逃生。

(2)经过优化处理，所有乘员按照优化后的疏散策略进行紧急疏散。

图4所示为横向联络通道间距150 m、列车与隧道间纵向疏散平台宽度1.0 m、人员均衡分布情况下，未优化和优化后的疏散模拟过程截图。从图4可以看到，未优化情况下人员主要在一个出口聚集拥堵，另一通道基本畅通，优化后的人员平均分布在两个通道进行疏散。进一步考虑列车与隧道纵向疏散平台宽度0.6 m、0.8 m的情况，通过模拟计算，得到如表1所示的人员疏散时间。

图4 人员疏散模拟过程截图

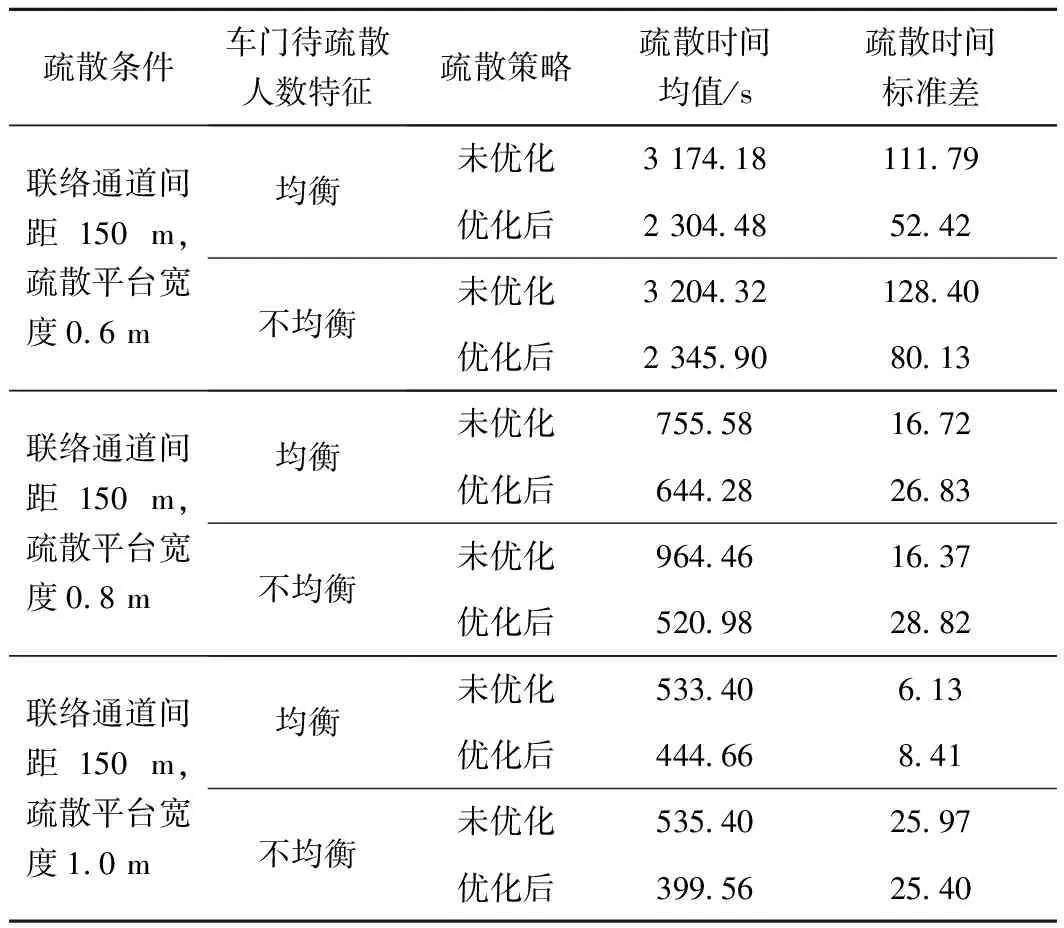
疏散条件车门待疏散人数特征疏散策略疏散时间均值/s疏散时间标准差联络通道间距150m，疏散平台宽度06m均衡未优化31741811179优化后2304485242不均衡未优化32043212840优化后2345908013联络通道间距150m，疏散平台宽度08m均衡未优化755581672优化后644282683不均衡未优化964461637优化后520982882联络通道间距150m，疏散平台宽度10m均衡未优化53340613优化后44466841不均衡未优化535402597优化后399562540

从模拟结果来看，采用优化算法将人员合理分配后，在联络通道间距150 m、列车与隧道间纵向疏散平台宽度0.6 m、0.8 m与1.0 m时：人员均衡分布的疏散条件下，人员疏散时间分别减少了27.40%、14.73%、16.64%；人员不均衡分布的疏散条件下，人员疏散时间分别减少了26.79%、45.98%、25.37%。可见，配流模型使得联络通道利用率大大提高，在一定程度上避免了大规模的堵塞发生。值得注意的是，当纵向疏散平台宽度为0.6 m时，人员疏散时间相对较长，这种情况下的人员疏散时间主要受到纵向疏散平台宽度的制约，行人仅能按单列行人方式疏散，如图5所示。增加纵向疏散平台宽度可以改善疏散人员疏散效率，从人员均衡分布、配流后的结果看，当列车与隧道联络通道间距由0.6 m增加到0.8 m时，疏散时间减少了72.04%。分析此时的疏散过程可以发现，随着纵向疏散平台宽度增加，人员在疏散过程的排列方式发生变化，疏散平台的通行效率得以提高，当纵向疏散平台宽度从0.8 m变为1.0 m时，疏散时间进一步下降，见表1。

实际上，旅客经纵向疏散平台疏散至无列车区域时，还可能会跨越疏散平台经由轨行区进行疏散。考虑上述情况，计算纵向疏散平台宽度1.0 m、人员均衡分布情况下，未优化和优化后的疏散过程如图6(a)和6(b)所示。从图中可以看出，优化后的客流疏散平均分布在两个通道，这与行人不可跨越疏散平台(图4)的情况相似。不同的是，在人员不可跨越疏散平台的情况下，两联络通道处基本畅通，瓶颈点集中在车厢区域，而在人员可跨越疏散平台时，车厢附近的瓶颈制约作用相对略小，联络通道则成为主要的瓶颈点。进一步考虑疏散时间及列车与隧道间纵向疏散平台宽度0.6 m、0.8 m、1.0 m的情况，得到各情景下的人员疏散时间见表2。

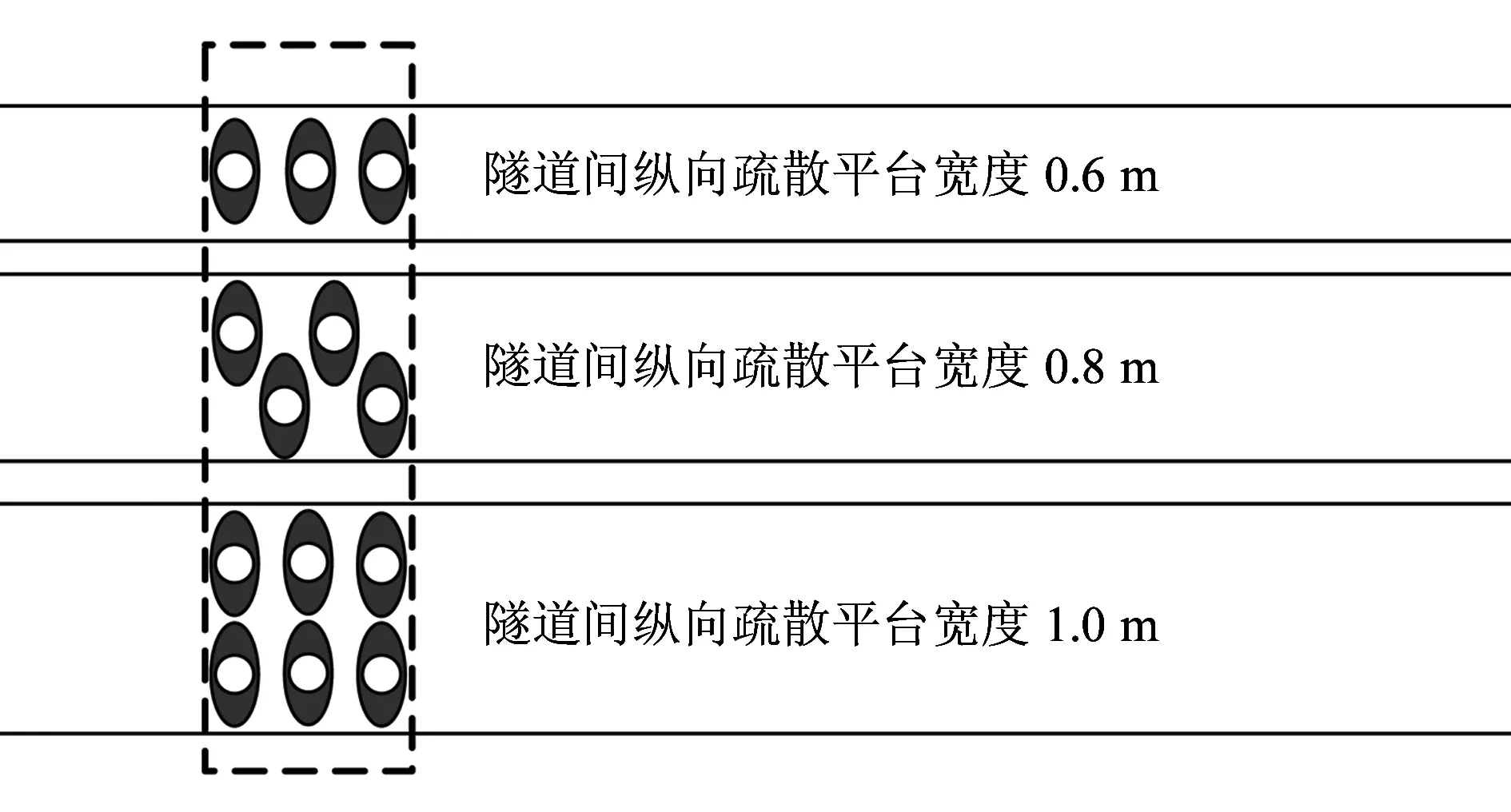
图5 疏散平台宽度对人员疏散方式的影响示意图

图6 可跨越疏散平台情境下的人员疏散模拟过程截图

疏散条件车门待疏散人数特征疏散策略疏散时间均值/s疏散时间标准差联络通道间距150m，疏散平台宽度06m均衡未优化1157102002优化后916262087不均衡未优化1202664131优化后763642883联络通道间距150m，疏散平台宽度08m均衡未优化582961004优化后45846772不均衡未优化658382652优化后356481033联络通道间距150m，疏散平台宽度10m均衡未优化552661267优化后435481163不均衡未优化494823225优化后338542201

从模拟结果来看，可跨越疏散平台情景下的人员疏散，在联络通道间距150 m、列车与隧道间纵向疏散平台宽度0.6 m、0.8 m与1.0 m时：人员均衡分布条件下，人员疏散时间分别减少了20.81%、21.36%、21.20%；人员不均衡分布条件下，人员疏散时间分别减少了36.50%、45.86%、31.58%。可见配流模型对于可跨越平台下的人员疏散优化也有十分明显的效果。值得注意的是，与不可跨越疏散平台的情况相比，可跨越疏散平台经由隧道疏散虽然在列车与隧道间疏散平台宽度从0.6 m增加至0.8 m时疏散时间有明显改善(从初始人员均衡分布，采用配流方法后的模拟结果看，减少了49.96%)，但是在疏散平台宽度从0.8 m 增加至1.0 m时改善并不明显(从人员均衡分布时配流后的结果看，疏散时间仅减少了5.01%)。同时，与人员不可跨越疏散平台的疏散情境相比，可跨越疏散平台的人员疏散，列车与隧道间纵向疏散平台宽度对人员的制约作用相对较小，列车与隧道间纵向疏散平台宽度0.6 m、人员均衡分布的情况下，不可跨越疏散平台的疏散情境下的疏散时间是可跨越疏散平台疏散情境的2.74倍，而从疏散效率来看，可跨越疏散平台疏散情境在疏散平台宽为0.8 m时就能基本接近不可跨越疏散平台的疏散情境下疏散平台宽为1.0 m时的疏散效率。

5 结论

考虑隧道疏散过程中车门、疏散平台与联络通道的约束作用，本文提出了一种行人配流模型，能够合理分配客流至不同疏散路径，实现疏散时间最短的目标。可通过手机软件或列车员引导等方式将该配流方法应用于隧道疏散过程。研究发现，在疏散过程跨越疏散平台和仅由纵向疏散平台疏散两种情境、三种疏散平台建设工况、两种人员分布情况下，都能明显降低行人疏散时间。与人员疏散过程可跨越疏散平台的情况相比，人员不可跨越疏散平台疏散时，疏散平台宽度对疏散时间的制约较大，在疏散过程安全可以保障的前提下，跨越疏散平台至隧道铁轨区域进行疏散可大幅提高疏散效率。在列车与隧道间疏散平台宽度为0.6 m时，人员受列车与隧道联络通道间距的制约作用明显，疏散时间较长，即便通过配流引导客流合理流动，允许乘客经由轨行区进行疏散，疏散效率依然较低。

需要注意的是，实际场景中的配流方案需要综合考虑联络通道间距、疏散平台宽度、列车编组辆数、停车位置等因素的影响，如何根据这些信息实现疏散策略的实时求解与优化需要开展进一步的研究工作。

参考文献：

[1]中华人民共和国铁道部.铁路隧道防灾救援疏散工程设计规范[M].北京:中国铁道出版社,2012.

[2]光明网.北京地铁5号线突发意外 隧道烟雾“倒灌”进车厢[EB/OL].http://politics.gmw.cn/2014-04/07/content_10919720.htm,2014-04-07/2014-05-23.

[3]侨报网.纽约地铁隧道内脱轨致19伤[EB/OL].http://news.uschinapress.com/2014/0502/976303.shtml,2014-05-02/2014-05-23.

[4]新华网.动车发生故障隧道内停车5小时旅客砸窗透气[EB/OL].http://news.xinhuanet.com/photo/2013-05/30/c_124786155.htm,2013-05-30/2014-0.

[5]FRIDOLF K,RONCHI E,NILSSON D,et al.Movement Speed and Exit Choice in Smoke-filled Rail Tunnels[J].Fire Safety Journal,2013,59:8-21.

[6]FRIDOLF K,NILSSON D,FRANTZICH H.The Flow Rate of People During Train Evacuation in Rail Tunnels:Effects of Different Train Exit Configurations[J].Safety Science,2014,62:515-529.

[7]COLINO M P,ROSENSTEIN E B.Tunnel Emergency Egress and the Mid-Train Fire[J].ASHRAE Transactions,2006,112(2).

[8]张念.高海拔特长铁路隧道火灾燃烧特性与安全疏散研究[D].北京:北京交通大学,2012.

[9]黎旭.城际轨道交通隧道疏散与防灾研究[D].成都：西南交通大学,2013.

[10]LIU S B,LO S M,MA J.On the Simulation for Rail Tunnel Evacuation with Cross-Passageways[C]//Pedestrian and Evacuation Dynamics 2012.Springer International Publishing,2014:425-433.

[11]陈绍宽,刘爽,肖雄,等.基于M/G/c/c模型的地铁车站楼梯通道疏散能力瓶颈分析[J].铁道学报,2012,34(1):7-12.

CHEN Shaokuan,LIU Shuang,XIAO Xiong,et al.M/G/c/c-based Model of Passenger Evacuation Capacity of Stairs and Corridors in Metro Stations[J].Journal of the China Railway Society,2012,34(1):7-12.

[12]胡清梅,方卫宁,李广燕,等.地铁车站出口布局对人群疏散性能的影响[J].铁道学报,2009,31(3):111-115.

HU Qingmei,FANG Weining,LI Guangyan,et al.Influence of Exit Layout of a Metro Station on Pedestrian Evacuation[J].Journal of the China Railway Society,2009,31(3):111-115.

[13]谢宝超,徐志胜.客运专线隧道火灾疏散研究[J].铁道学报,2013,35(8):102-108.

XIE Baochao,XU Zhisheng.Fire Evacuation in Passenger Dedicated Line Tunnel[J].Journal of the China Railway Society,2013,35(8):102-108.

[14]毛军,郗艳红,李胜利,等.地铁车站火灾防灾减灾关键技术的研究[J].铁道学报,2009,31(4):115-120.

MAO Jun,XI Yanhong,LI Shengli,et al.Key Technologies of Prevention and Control of Subway Station Fire[J].Journal of the China Railway Society,2009,31(4):115-120.

[15]北京城建设计总院.GB 50157—2003 地铁设计规范[S].北京:中国计划出版社,2003.

[16]刘斌,马剑,牟瑞芳,等.区分障碍物特性的客车乘客疏散模型与分析[J].交通运输系统工程与信息,2015,15(4):173-180.

LIU Bin,MA Jian,MOU Ruifang,et al.Modeling and Analysis of Modern Tram Evacuation Performance Considering Effect of Obstacles[J].Journal of Transportation Systems Engineering and,2015,15(4):173-180.

[17]马剑.相向行人流自组织行为机理研究[D].合肥：中国科技大学,2010.

[18]李清泉,李秋萍,方志祥.一种基于时空拥挤度的应急疏散路径优化方法[J].测绘学报,2011,40(4):0-441.

LI Qingquan,LI Qiuping,FANG Zhixiang.An Emergency Evacuation Routing Optimization Method Based on Space-time Congestion Concept[J].Acta Geodaetica et Cartographica Sinica,2011,40(4):0-441.

[19]何健飞,刘晓.基于拥挤度的地铁应急疏散路径优化方法[J].中国安全科学学报,2013,23(2):166-171.

HE Jianfei,LIU Xiao.A Subway Emergency Evacuation Routing Optimization Method Based on Congestion Degree[J].China Safety Science Journal,2013,23(2):166-171.