钢管混凝土收缩变形与钢管混凝土拱收缩应力

陈宝春，赖秀英

(福州大学 土木工程学院，福建 福州 350108)

钢管混凝土拱桥已在我国公路与城市桥梁中广泛应用，近年来在高速铁路桥梁中的应用也不断增多。钢管混凝土作为组合结构，管内混凝土收缩产生的应力是结构设计必须考虑的问题。收缩应力包括收缩自应力和收缩次应力。钢管混凝土拱肋作为组合构件，管内混凝土收缩受到钢管的约束，钢管混凝土构件的收缩值小于管内混凝土的收缩值，根据应变协调条件，将产生钢管受压、混凝土受拉的应力称为收缩自应力。对于超静定的钢管混凝土拱，拱肋的收缩会在结构中产生附加内力(次内力)，由收缩次内力引起的应力称为收缩次应力。钢管混凝土拱收缩应力计算的关键是管内混凝土收缩量的确定。由于管内混凝土处于密闭状态且受钢管约束，其收缩规律与普通混凝土不完全相同。

国内外已开展钢管混凝土构件的收缩变形试验研究[1-8]，但试验结果离散性较大，规律性较差，由于这些试验主要是因钢管混凝土徐变试验需要排除收缩变形的影响而进行的对比试验，未对影响混凝土收缩变形的因素进行针对性研究。专门针对收缩问题开展的试验未见报道。为此，本文从钢管混凝土拱桥常用配合比及特殊工作性能的要求出发，开展以混凝土强度等级、粉煤灰掺量、钢管直径以及含钢率为主要参数的钢管混凝土收缩变形试验，了解钢管混凝土的收缩特性，为选择合理的收缩预测模型打下基础。

对于混凝土收缩变形的计算，文献[9]采用CEB-FIP MC78模型，文献[10]采用CEB-FIP MC90模型。对于钢管混凝土拱桥的收缩变形计算，文献[11，12]均未作明确规定，但对于徐变变形分别推荐采用ACI 209R-92模型和CEB-FIP MC90模型。文献[13]则规定采用实测值或按文献[10]的规定计算，即采用CEB-FIP MC90。CEB-FIP MC78、CEB-FIP MC90和ACI 209R-92同时也是目前国际上认可度较高的3种收缩预测模型，但它们应用于钢管混凝土收缩变形值的预测效果，目前尚未见深入分析。为此，本文将在试验研究的基础上，对这3种混凝土收缩预测模型进行对比分析，为实际工程应用选择合适的计算模型提供参考。

对于混凝土和钢筋混凝土超静定结构由于收缩变形引起的次内力，文献[9]提出采用等效降温法计算。在相当一段时间内，设计者也多采用等效降温法计算钢管混凝土拱桥收缩次内力。文献[14]的分析表明，等效降温15～20 ℃的计算结果明显偏大，但由于缺乏具体的钢管混凝土收缩试验值，未进行深入分析。为此，本文通过对常用管内混凝土收缩应变的计算，对等效降温法的应用作进一步探讨。同时，本文还对收缩自应力和某铁路钢管混凝土拱桥的收缩应力进行算例分析。

1 钢管混凝土构件收缩试验

1.1 试件参数选择

收缩是混凝土在无荷载作用下随时间而产生的变形，是混凝土本身的属性，它主要由化学收缩(自收缩)和干缩组成。钢管混凝土中的核心混凝土处于密闭环境，没有与外界发生水分交换，相当于保水养护，因此只有自收缩变形，没有干缩或干缩很小可以忽略。

影响混凝土收缩的因素主要有养护条件、水灰比、水泥浆用量、水泥的品种等。在养护条件方面，管内混凝土属密闭养护，但边界受钢管的约束。研究表明，暴露在大气环境中的普通混凝土水分扩散与构件的截面尺寸关系较大，截面尺寸越大，水分扩散越慢，干缩值越小；反之亦然。钢管混凝土截面尺寸对管内混凝土收缩的影响，现有研究没有定论。文献[1]对两个试件的测试结果表明钢管混凝土构件的收缩变形与直径成反比。文献[2]试验研究结果表明收缩值与构件的尺寸关系不大。本文将钢管直径作为一个参数，对此问题作进一步探讨。同时，钢管混凝土的收缩与含钢率有关，钢管管径与壁厚的变化影响含钢率，本文将含钢率作为一个参数来研究。

钢管混凝土拱肋管内混凝土的强度一般为C30～C60，C40和C50居多。管内混凝土的浇注常采用泵送法，要求混凝土坍落度大、和易性好，且不泌水不离析。为同时达到强度与施工性能要求，一般通过添加外加剂和矿物掺合料(如粉煤灰)来实现[15]。本试验以混凝土强度和粉煤灰掺量为混凝土材料的主要参数，考虑水灰比、水泥浆用量对收缩的影响。钢管混凝土拱桥一般采用硅酸盐水泥，故本文没有将水泥品种作为参数分析。

1.2 试件设计

钢管混凝土拱桥采用的钢管直径一般在600～1 300 mm 之间，最常用的是1 000 mm。考虑到试验条件，本试验中的钢管直径范围定为165～1 000 mm，除直径600 mm和1 000 mm的钢管壁厚为8 mm外，其余均为2 mm，钢管长度为600 mm。含钢率的变化范围为0.030～0.056。

考虑混凝土强度等级和粉煤灰掺量2个参数，管内混凝土共设计了7组配合比M1～M7，其中M1设计强度等级为C40，M2为C60，M3～M7为C50并加入粉煤灰掺量参数(粉煤灰掺量0%～40%)。根据工程经验和规范要求，管内混凝土入泵时坍落度宜为200～260 mm，水胶比不宜超过0.35，设计时管内混凝土配合比取坍落度230 mm，水胶比0.29～0.41(M1配合比在满足坍落度和强度要求后，水胶比稍超过0.35，其余均小于0.35)。混凝土采用的材料：福建炼石牌P.O 425普通硅酸盐水泥；花岗岩碎石，最大粒径30 mm；闽江河沙；Ⅱ级粉煤灰；福州创先工程材料有限公司CX-8聚羧酸减水剂，减水率25%。7组混凝土配合比及其性能见表1。

本试验共设计钢管混凝土收缩试件11个，根据主要参数钢管直径(含钢率)、混凝土强度和粉煤灰掺量分为3组；另设计一组共2个(参数相同)的素混凝土对比试件。试件按组别、钢管直径、混凝土强度和粉煤灰掺量进行编号，S为钢管混凝土试件、P为素混凝土试件；S1以钢管直径为参数，S2以混凝土强度为参数，S3以粉煤灰掺量为参数，如S1-D2-C50-10试件是第Ⅰ组钢管混凝土试件、钢管直径为219 mm、混凝土强度等级为C50、粉煤灰掺量为10%。试件主要参数见表2。

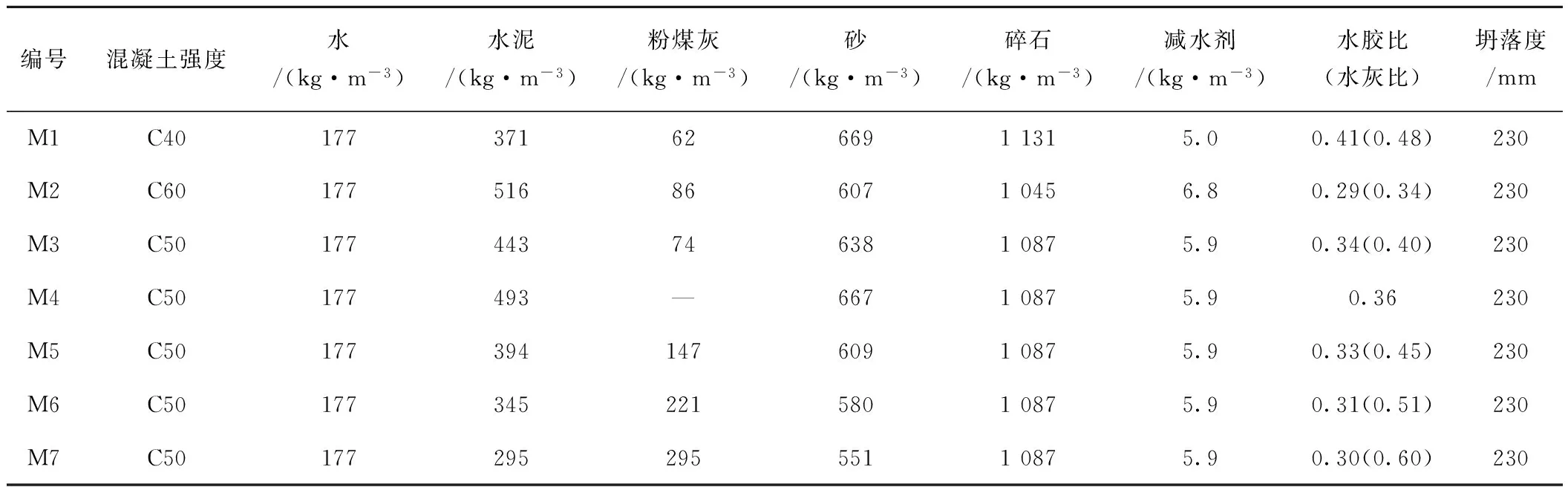
表1 混凝土配合比

表2 钢管混凝土收缩试件参数一览表

1.3 试件制作与测试装置

对于钢管混凝土试件，按要求的长度和外直径加工空钢管及两端钢盖板，在浇注混凝土之前先将一端的盖板焊接，另一端待混凝土浇注完成且体积较稳定后再焊接。对于素混凝土试件，由于要测量密闭环境下的收缩变形，在模板内侧铺有隔水塑料薄膜，混凝土浇注成形拆模后在薄膜外侧涂上石蜡保持混凝土处于密闭状态。

为消除温度影响，将试件置于专用的密闭实验室内，通过自动控温系统控制环境温度为(24±1)℃。由于所有试件的混凝土均处于密闭环境，环境湿度的影响较小，故未对环境湿度进行控制。

图1 部分试验构件照片

钢管混凝土的纵向收缩变形测试装置如图2所示。在钢管侧面对称位置预留了6个(每侧3个)直径15 mm的孔，长100 mm、一端开8 mm孔的钢棒穿过预留孔，未开孔端埋置于混凝土中，直径6 mm的刚性钢杆穿过外部端8 mm的孔。带孔钢棒外部端配有螺纹和螺丝杆，用于固定千分表和刚性钢杆。试验测试原理为：采用千分表测量钢管混凝土构件纵向两个螺丝杆的相对变形，此相对变形与其初始间距的比值即为钢管混凝土构件的收缩应变。

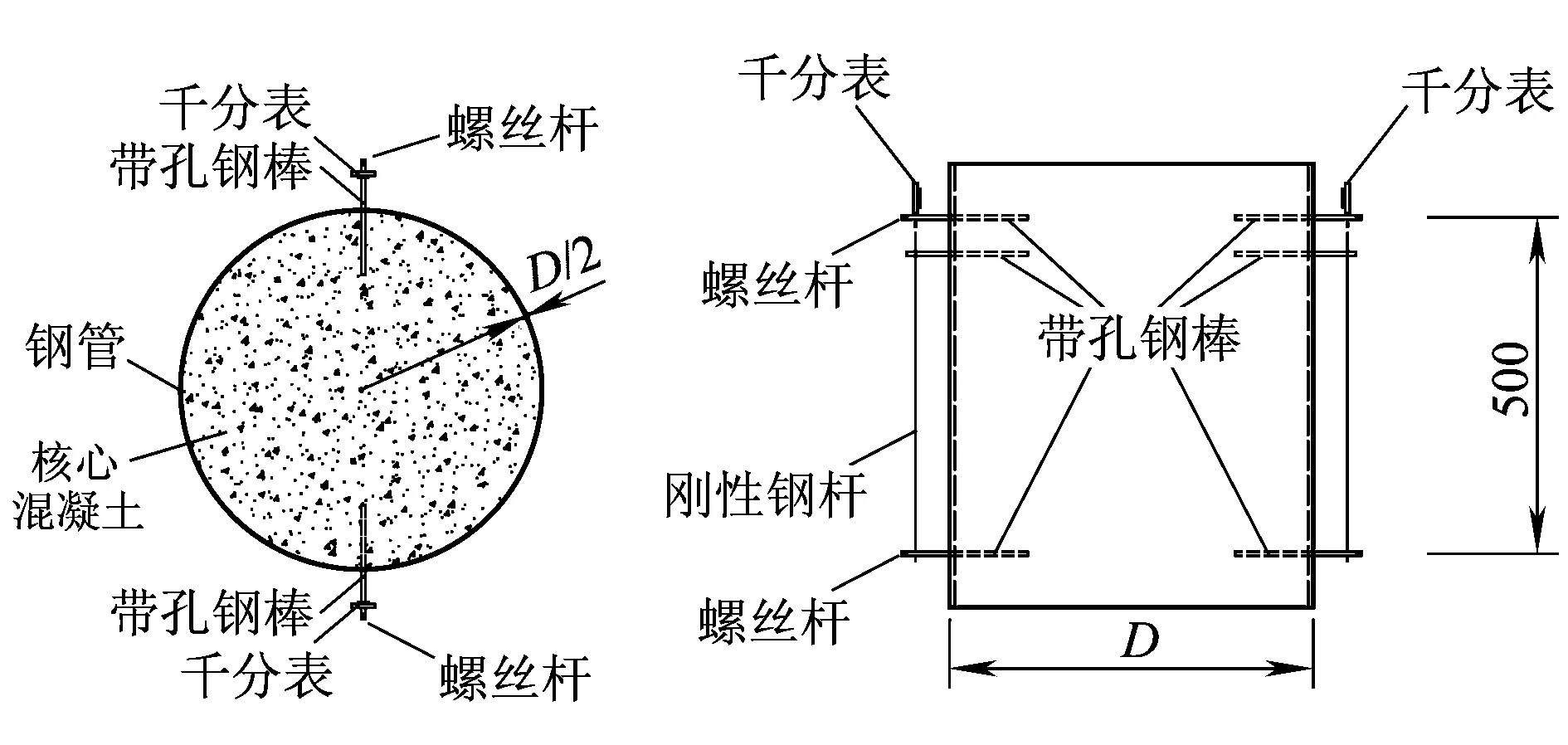
图2 钢管混凝土试件收缩变形试验装置图

测量装置安装在混凝土终凝前完成，埋置带孔钢棒时严格进行几何对中并与试件轴线垂直，旋紧螺丝杆卡紧刚性钢杆和千分表，使千分表下部端头与刚性钢杆上部端头稳定接触，然后记录千分表的初始读数。装置安装完毕后，测量两螺丝杆的初始间距。

1.4 试验总体情况

图3为全部钢管混凝土构件的收缩实测曲线。从图3可以看出，所有试件收缩有相似的发展规律，但数值并不相同。试验共进行了180 d，收缩在60 d以前发展较快，60 d时达到了180 d总收缩应变的75%以上，在此之后收缩应变增长相对缓慢，100 d时达到总收缩应变的90%以上，随后应变曲线渐趋水平，应变增长趋于稳定。

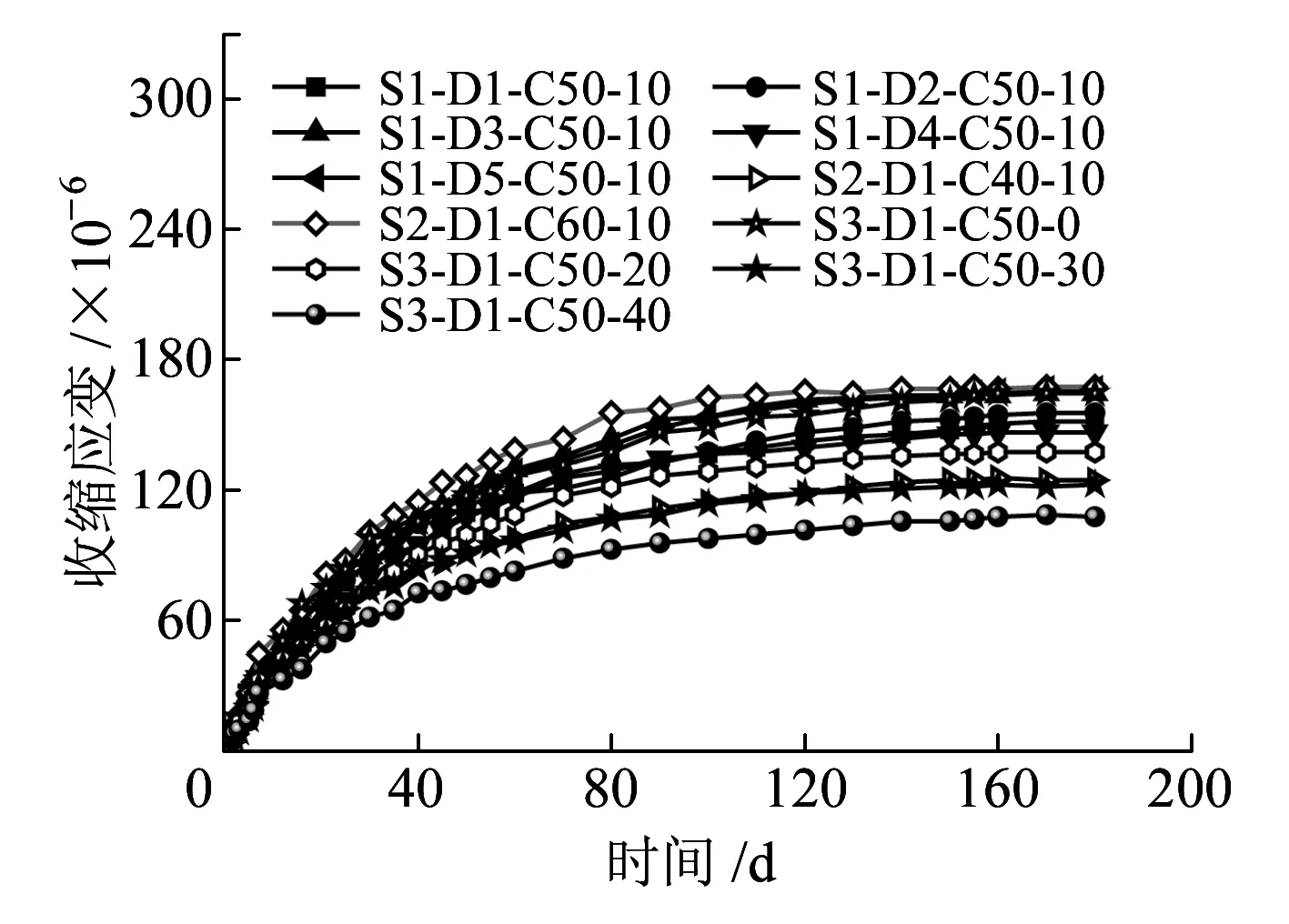
图3 全部钢管混凝土构件收缩实测值

由图4可见，钢管混凝土构件与密闭素混凝土构件的收缩应变规律相似，但钢管混凝土构件收缩小于后者。钢管混凝土构件180 d的收缩应变值比素混凝土构件小22.8%，钢管混凝土构件的60 d和100 d收缩值分别为总收缩值的76.9%和90.1%，而素混凝土构件对应比例分别为80.2%和91.9%，即钢管混凝土构件的早期收缩增长速度较素混凝土慢。

图4 钢管混凝土与素混凝土实测收缩曲线的比较

1.5 试验结果参数分析

1.5.1 钢管混凝土构件收缩计算

如图5所示，对于一端固结、一端自由的钢管混凝土构件，假定钢管与核心混凝土完全黏结，在混凝土自由(或无约束)收缩变形Δc作用下，钢管混凝土将产生Δsc的收缩变形，根据截面应变协调条件，由力的平衡原理∑N=0可知

( 1 )

( 2 )

式中：Δc为混凝土在无约束状态下的自由收缩变形；Δsc为钢管混凝土的收缩变形；L为构件计算长度；Es为钢材弹性模量；Ec为混凝土弹性模量；As为钢管混凝土单圆管钢管截面面积；Ac为钢管混凝土单圆管混凝土截面面积。

图5 钢管混凝土收缩变形示意

由式( 2 )可计算考虑钢管混凝土构件的收缩应变，见式( 3 )。

( 3 )

式中：εc为混凝土的收缩应变；εsc为钢管混凝土的收缩应变。

对于超静定结构，构件的收缩变形或收缩应变将在结构中产生收缩次内力，对应的是截面上的收缩次应力。

钢管混凝土作为组合构件在截面上存在收缩自应力。如图5所示，钢管受到的约束变形Δs与钢管混凝土构件的变形Δsc相同，管内混凝土受到的约束变形为混凝土自由变形减去钢管混凝土变形，即Δc-Δsc。据此，可按式( 4 )和式( 5 )计算截面收缩自应力，其中管内混凝土受拉，钢管受压。

( 4 )

( 5 )

式中：σsh，c为收缩引起的核心混凝土拉应力；σsh，s为收缩引起的钢管压应力。

从上述分析可知，无论是收缩次应力还是收缩自应力，都与钢管混凝土的收缩变形或应变有关。更进一步，由式( 2 )可知，它们都与管内混凝土的自由收缩值、钢管与管内混凝土的相对刚度有关。

1.5.2 粉煤灰掺量

粉煤灰掺量是管内混凝土自由收缩值的主要影响因素之一。图6为粉煤灰掺量对钢管混凝土收缩应变值影响的试验结果对比。由图6(a)可知，钢管混凝土收缩应变随着粉煤灰掺量的增加而减小。由于粉煤灰可替代部分水泥，随着粉煤灰掺量的提高，水泥用量减少，早期混凝土的硬化速度降低，相对减小了内部自干燥量，即减少了混凝土的收缩。

图6(b)180 d收缩应变显示，粉煤灰掺量与收缩应变的关系基本呈线性变化，即随着粉煤灰掺量的增加，收缩应变线性下降，以掺量0%为基准，粉煤灰掺量10%、20%、30%和40%的收缩应变分别较其减少6.1%、16.4%、25.5%和34.5%。

(a)过程曲线

(b)收缩值-粉煤灰掺量关系曲线图6 粉煤灰掺量对钢管混凝土收缩的影响

1.5.3 混凝土强度等级

混凝土强度等级不同，配合比不同，将影响管内混凝土的自由收缩值。图7为不同强度等级钢管混凝土收缩结果对比。由图7(a)可以看出，随着混凝土强度等级的提高，钢管混凝土收缩应变增大。这是由于混凝土强度越高，水胶比越低，混凝土中胶凝材料越多，水化需要的水分增多，但混凝土中可用于参与水化反应的水分却减少了，从而导致管内混凝土的自干燥现象加剧，增大了混凝土的收缩应变。从图7(b)不同龄期收缩应变与混凝土强度等级的关系可以看出，随着混凝土强度等级的提高，钢管混凝土的收缩基本呈线性增长；180 d收缩应变，C60混凝土收缩较C50增大10.5%，C50较C40增大21.6%，C60较C40增大34.4%。

(a)过程曲线

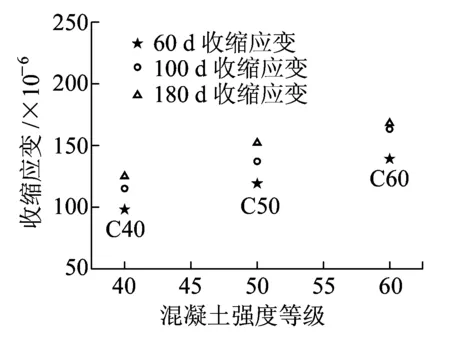
(b)收缩值-混凝土强度等级关系曲线图7 混凝土强度等级对钢管混凝土收缩的影响

1.5.4 管径与含钢率

图8(a)为第一组不同管径试件的收缩曲线，曲线始端几乎重合，总收缩量稍有不同。图8(b)为180 d 的收缩值(括号外)与管径(括号内)的对应关系。比较可知，各试件180 d的收缩值稍有差异，应变值为(147～167)×10-6，最大差值为12%；管径的最大差值达6倍，收缩应变与管径没有明确关系，即可以不考虑管径的影响，与文献[2]的结论一致。同时，这也表明钢管混凝土收缩的尺寸效应不明显，本文进行的试验结果可推广到管径较大的实际工程应用中。

(a)过程曲线

(b)180 d收缩应变-管径关系曲线图8 钢管直径对钢管混凝土收缩应变的影响

含钢率是钢管混凝土构件的重要指标，从钢管和管内混凝土的相对刚度来说，含钢率比管径更能反映对收缩的影响。由图9可以看出，含钢率与收缩应变呈较明显的线性关系，随着含钢率的增大，实测钢管混凝土收缩应变减少。为解释这一现象，令α=As/Ac，n=Es/Ec，则式( 3 )可以转化为

( 6 )

式中：α为截面含钢率；n为钢管与核心混凝土弹性模量比。

图9 截面含钢率对钢管混凝土收缩应变的影响

由式( 6 )可知，当核心混凝土的自由收缩、钢与核心混凝土弹性模量比一定时，随着含钢率的增大，钢管对管内混凝土自由收缩的约束效应增大，钢管混凝土的收缩应变减小。

2 钢管混凝土收缩预测模型

2.1 密闭素混凝土收缩预测模型

由上文可知，钢管混凝土的收缩与管内混凝土的自由收缩关系密切。本节通过选取目前常用的3种普通混凝土收缩模型与密闭素混凝土试件收缩试验结果进行对比，选择合适的收缩预测模型。这3种模型即CEB-FIP MC78模型、CEB-FIP MC90模型和ACI 209R-92模型，本文不作详细介绍，分别参见文献[16]、文献[10]和文献[17]。

本试验第Ⅳ组构件为素混凝土密闭构件的收缩试验。将3种模型考虑的各种参数如环境相对湿度、混凝土强度、水泥含量、构件理论厚度等分别代入相关计算公式，得到CEB-FIP MC78模型、CEB-FIP MC90模型和ACI 209R-92模型预测的180 d收缩应变分别为33×10-6、103×10-6和198×10-6，与实测值比值分别为0.17、0.52和1.01，ACI 209R-92模型预测最接近实测值，CEB-FIP MC90次之，CEB-FIP MC78最差，后两个模型预测值均偏低。

图10是三种模型的预测曲线与收缩应变实测曲线，从图10可以看出，ACI 209R-92模型预测结果最好，180 d收缩实测值与预测值的判定系数R2为0.989，接近1。

2.2 钢管混凝土收缩预测模型

应用3种收缩预测模型计算11个钢管混凝土试件的收缩应变值。计算时，各影响参数按照实际取值。考虑核心混凝土处于密闭环境，环境相对湿度取90%。ACI 209R-92模型中，密闭环境核心混凝土的收缩变形与构件尺寸无关，构件尺寸影响系数γvs取1.0。CEB-FIP MC90模型与CEB-FIP MC78模型中考虑构件尺寸效应，构件理论厚度按实际取值。将计算所得的混凝土收缩应变值代入式( 3 )，求得3种模型预测的180 d钢管混凝土构件收缩应变值，将其与实测的收缩应变值对比，计算结果列于表3。

图10 素混凝土构件收缩实测值与模型计算值比较

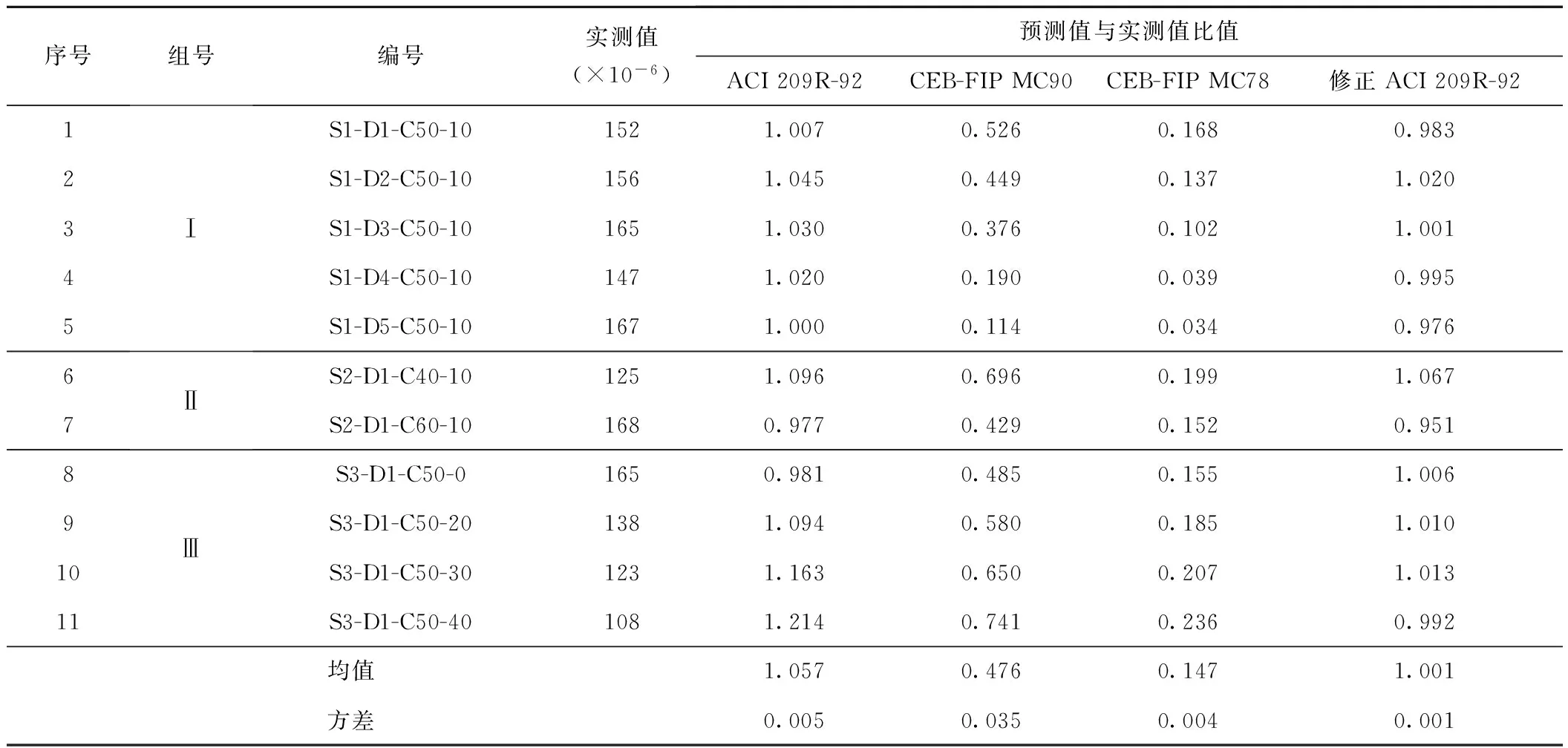
序号组号编号实测值(×10-6)预测值与实测值比值ACI209R-92CEB-FIPMC90CEB-FIPMC78修正ACI209R-9212345ⅠS1-D1-C50-101521.0070.5260.1680.983S1-D2-C50-101561.0450.4490.1371.020S1-D3-C50-101651.0300.3760.1021.001S1-D4-C50-101471.0200.1900.0390.995S1-D5-C50-101671.0000.1140.0340.97667ⅡS2-D1-C40-101251.0960.6960.1991.067S2-D1-C60-101680.9770.4290.1520.951891011ⅢS3-D1-C50-01650.9810.4850.1551.006S3-D1-C50-201381.0940.5800.1851.010S3-D1-C50-301231.1630.6500.2071.013S3-D1-C50-401081.2140.7410.2360.992均值1.0570.4760.1471.001方差0.0050.0350.0040.001

从表3最后两行的统计分析可知，与密闭素混凝土收缩的预测值相似，3个模型对钢管混凝土试件收缩的预测值与实测值对比中，ACI 209R-92吻合最好，CEB-FIP MC90次之，CEB-FIP MC78最差。

从前文可知，CEB-FIP MC78模型、CEB-FIP MC90模型计算的收缩值主要是干燥收缩，如其中的构件理论厚度、环境相对湿度和混凝土强度的影响等都是在考虑干燥收缩的基础上提出的。两个模型均没有考虑粉煤灰掺量对收缩的影响。

CEB-FIP MC78没有考虑混凝土强度对收缩的影响。CEB-FIP MC90模型虽然有考虑，但它是基于混凝土强度对干燥收缩而不是化学收缩的影响。混凝土强度越大，水胶比越小，混凝土中水分含量越少，其干燥收缩越小，这与密闭状态下混凝土的化学收缩规律相反，因此不能正确反映密闭环境下混凝土的收缩规律。

ACI 209R-92模型将影响混凝土收缩的各因素分离出来，易于根据密闭环境下的混凝土条件来设定相应参数。如密闭环境下混凝土收缩不受构件尺寸的影响，可以将构件尺寸影响系数取为1.0；混凝土强度和粉煤灰掺量的影响可以通过水泥含量来反映。

进一步分析可知，表3中ACI 209R-92模型对第Ⅲ组粉煤灰掺量稍大的试件预测精度较差。这主要是由于随着粉煤灰掺量的增加，水泥用量减少，粉煤灰的活性一般较低，从而降低了混凝土的收缩变形，ACI 209R-92模型对此没有充分考虑。

在试验资料基础上，对ACI 209委员会推荐的混凝土收缩应变计算公式，引入粉煤灰掺量修正系数γfa，得到式( 7 )。

( 7 )

式中：t为收缩时间；γfa为粉煤灰掺量修正系数，按式( 8 )计算；(εsh)u为最终收缩值，按式( 9 )计算。

γfa=-0.521 5k1+1.026 4

k1=0.10～0.40

( 8 )

(εsh)u=(780×10-6)·γCP·γλ·γvs·

γs·γψ·γc·γα

( 9 )

式中：780×10-6为标准条件下自由收缩应变；γCP、γλ、γvs、γs、γψ、γc、γα为偏离标准条件时的校正系数，各项依次为考虑初始养护条件、年环境相对湿度、构件体积-表面积比、混凝土坍落度、细骨料含量、水泥含量和混凝土含气量等因素的修正系数，具体计算公式见文献[17]。

图11为部分试件实测值与预测值的发展曲线。其余试件的结果相似，限于篇幅，没有示出。结合图11 和表3可见，ACI 209R-92模型预测值与实测值比值的均值为1.057，方差为0.005。除构件S3-D1-C50-30和S3-D1-C50-40误差超10%外，其余均在10%以内。

(a)S3-D1-C50-0试件

(b)S1-D1-C50-10试件

(c)S3-D1-C50-20试件

(d)S3-D1-C50-30试件图11 部分试件收缩应变实测曲线与预测曲线

第Ⅲ组试件以粉煤灰掺量为参数，ACI 209R-92模型预测值与实测值比值的均值为1.092，方差为0.008；预测效果稍差于全体试件的效果。修正后ACI 209R-92模型预测值与实测值比值的均值为1.000 8，方差为0.000 3，预测精度有明显提高。对于所有11个试件，修正后的比值均值为1.001，方差0.001，预测精度有较大提高。应该指出的是，实际工程中，粉煤灰掺量一般为10%～20%，小于本试验的掺量范围(0%～40%)，而从表3可知，误差较大的是粉煤灰掺量大于20%的2根试件。因此，对于粉煤灰掺量不大于20%的构件仍可直接应用ACI 209R-92模型进行收缩计算，若粉煤灰掺量大于20%可考虑对其进行修正。本文以粉煤灰掺量为参数的试件仅4个(其中1个粉煤灰掺量为零)，试件偏少，因此上述修正的合理性还有待进一步验证。

2.3 预测值与其他试验结果的比较

为了扩大样本，将文献[1-8]的23根钢管混凝土收缩试验构件的收缩实测值剔除明显不合理的值后，与本文3种收缩模型预测值的比较列于表4和图12。比较结果与上文相似，ACI 209R-92模型预测值与实测值吻合最好，二者比的均值1.180，方差0.215；CEB-FIP MC90次之，均值0.569，方差0.197；CEB-FIP MC78最差，均值0.252，方差0.030。

图12 其他试件收缩实测值与模型预测值的比值对比

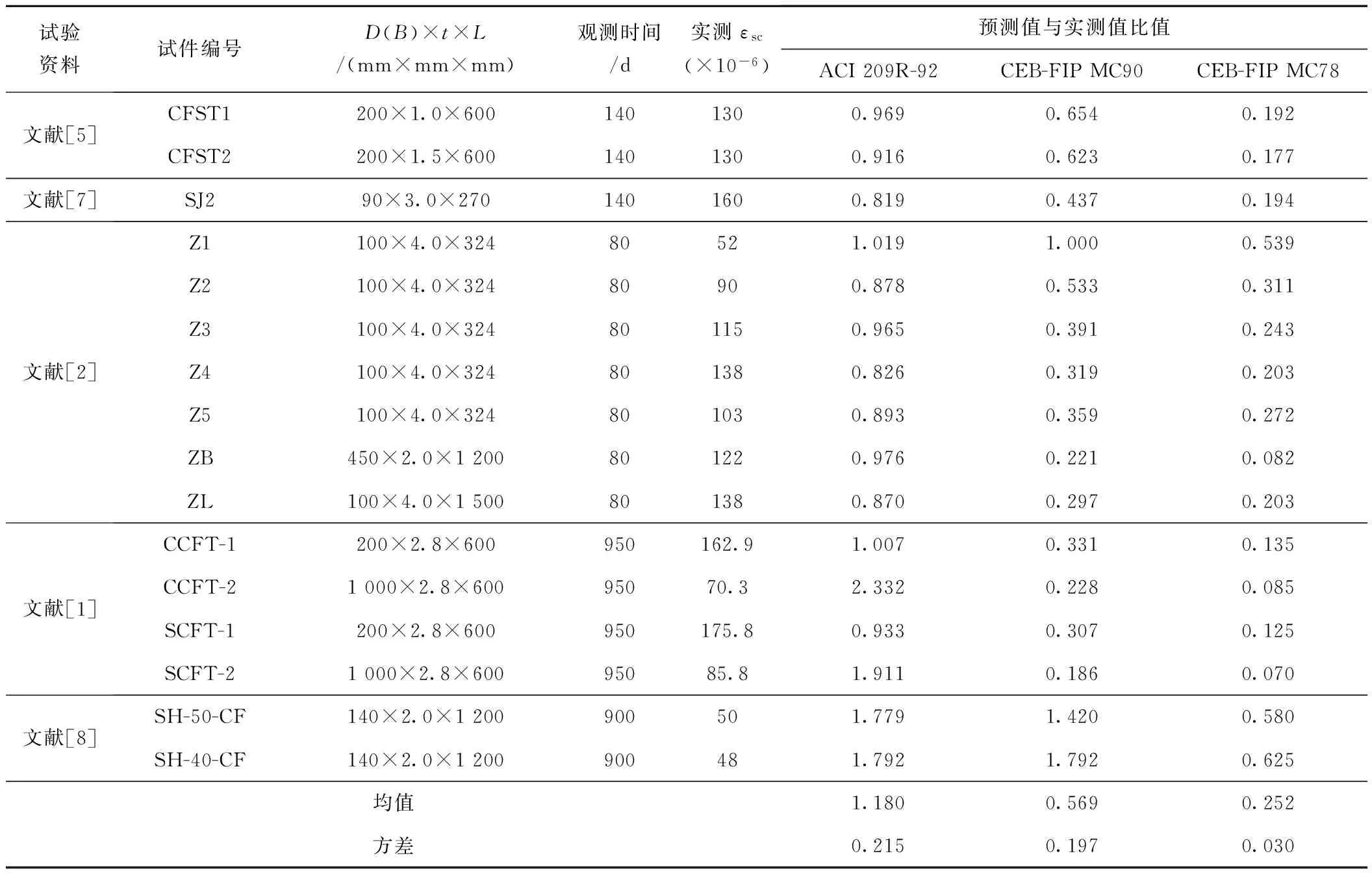
试验资料试件编号D(B)×t×L/(mm×mm×mm)观测时间/d实测εsc(×10-6)预测值与实测值比值ACI209R-92CEB-FIPMC90CEB-FIPMC78文献[5]CFST1200×1.0×6001401300.9690.6540.192CFST2200×1.5×6001401300.9160.6230.177文献[7]SJ290×3.0×2701401600.8190.4370.194文献[2]Z1100×4.0×32480521.0191.0000.539Z2100×4.0×32480900.8780.5330.311Z3100×4.0×324801150.9650.3910.243Z4100×4.0×324801380.8260.3190.203Z5100×4.0×324801030.8930.3590.272ZB450×2.0×1200801220.9760.2210.082ZL100×4.0×1500801380.8700.2970.203文献[1]CCFT-1200×2.8×600950162.91.0070.3310.135CCFT-21000×2.8×60095070.32.3320.2280.085SCFT-1200×2.8×600950175.80.9330.3070.125SCFT-21000×2.8×60095085.81.9110.1860.070文献[8]SH-50-CF140×2.0×1200900501.7791.4200.580SH-40-CF140×2.0×1200900481.7921.7920.625均值1.1800.5690.252方差0.2150.1970.030

3 钢管混凝土拱桥收缩应力分析

由前文分析可知，ACI 209R-92模型能较好预测钢管混凝土的收缩应变，虽然在考虑粉煤灰掺量影响方面还有待改进，一般钢管混凝土拱桥管内混凝土的粉煤灰掺量不高于20%[15]，故本章分析中的收缩计算将以ACI 209R-92模型为主。

3.1 钢管混凝土收缩应变

根据文献[15]给出的一般钢管混凝土拱肋管内混凝土的配合比等参数，应用ACI 209R-92模型及式( 3 )，计算得180 d管内混凝土的收缩应变为εc=(172～247)×10-6，钢管混凝土的收缩应变为εsc=(78～208)×10-6。计算时，取环境相对湿度90%；混凝土坍落度200～260 mm，细骨料含量32%～44%，水泥含量450～550 kg/m3；含气量小于2.5%；构件尺寸影响系数取1.0。

对文献[15]和文献[18]给出的部分实例，采用同样的计算方法，计算混凝土的收缩应变εc=(190～214)×10-6，钢管混凝土的收缩应变εsc=(132～157)×10-6，其范围在前述计算结果中。具体计算结果见表5。

因此，对于一般钢管混凝土拱桥收缩作用估算时，可取管内混凝土的收缩应变εc=(172～247)×10-6、钢管混凝土的收缩应变εsc=(78～208)×10-6。

3.2 收缩应力计算

3.2.1 收缩自应力计算

应用式( 4 )和式( 5 )，取管内混凝土的收缩应变εc=(172～247)×10-6，对于常见的钢管混凝土拱肋，截面自应力计算结果见表6。部分工程应用的计算结果见表5的最后两列。文献[13]中规定，持久状况下钢管混凝土拱肋的钢管应力不宜大于0.8fy(fy为钢管设计强度)。从表6可见，管内混凝土收缩自应力产生的钢管应力为16.1～42.8 MPa，达到(4.7%～19.0%)fy，在设计计算中应考虑。

对于管内混凝土，收缩自应力值一般已超过其抗拉设计强度，但由于钢管混凝土拱以受压为主，是否会引起管内混凝土开裂，应综合计算确定。

3.2.2 收缩次应力计算

钢管混凝土超静定拱由于混凝土收缩引起的次应力计算，目前有两种方法：①等效降温的解析法；②有限元法。两种计算方法的原理与普通混凝土均相同，但要考虑钢管混凝土拱组合截面的特性。文献[14]对这两种方法进行详细比较，结果表明两种计算方法均可行，但是等效降温15～20 ℃计算钢管混凝土拱桥的收缩次内力结果偏大，采用有限元法直接计算更能反映收缩引起的应力效应。

表5 钢管混凝土拱桥工程实例拱肋混凝土收缩εsc

表6 常见钢管混凝土拱肋截面自应力 MPa

由前文分析可知，对常用钢管混凝土收缩应变值的计算，εsc=(78～208)×10-6，根据文献[14]介绍的方法计算，等效降温值为7.7～20.6 ℃。对于表5中的13座桥梁，钢管混凝土拱肋的收缩应变εsc=(132～157)×10-6，等效降温值为13.1～15.5 ℃。

文献[9]规定采用等效降温15～20 ℃计算混凝土收缩引起的次内力(次应力)，与本文等效降温7.7～20.6 ℃的结果相比，有时相近，有时则偏于保守。同时，由于等效降温值范围较大，具体桥梁如何选择等效降温值不易确定，可以直接通过程序计算确定。此外，采用等效降温法计算，无法考虑收缩自应力，仍然需要计算管内混凝土的收缩应变。当然，在初步设计估算时，等效降温值可以参考，但宜保守选用。

3.3 算例分析

收缩次内力与实际桥梁的结构相关性较大，难以像自应力一样进行一般性分析，本文以黄河特大桥为例进行计算分析，综合计算收缩自应力和收缩次应力。

黄河特大桥为一座跨径380 m的铁路钢管混凝土提篮拱桥。采用桥梁结构分析软件MIDAS Civil进行收缩计算，选择双单元法建模来考虑钢管对管内混凝土收缩的约束作用，全桥共707个节点，划分成1 437个单元。桥梁具体情况与建模见文献[19]。

采用ACI 209R-92模型进行收缩应力计算。根据该桥的实际情况，计算参数取值为：收缩开始龄期3 d，年平均相对环境湿度90%，体积-面积比系数取1.0，湿润养护，混凝土强度等级C50，细骨料含量39.5%，水泥含量500 kg/m3，坍落度220 mm，拌合物含气量2.5%。CEB-FIP MC90模型的参数取值为：收缩开始龄期3 d，年平均相对环境湿度90%，混凝土强度等级C50。收缩分析时间从拱肋空钢管合龙后计算至成桥后365 d。

考虑该桥为铁路桥梁，在有限元计算中还采用文献[20]的收缩模型，即CEB-FIP MC78模型进行该桥的收缩计算。此外，还参照钢筋混凝土拱桥，按等效温降15 ℃进行收缩次内力计算，并将结果与收缩预测模型的有限元计算结果进行比较。以收缩作用产生的钢管最大应力值为分析对象，它出现在拱脚截面的下弦杆，见表7。

表7 拱脚截面下弦杆收缩应力计算结果 MPa

从表7可以看出，ACI 209R-92模型计算的收缩自应力、收缩次应力和总应力均大于CEB-FIP MC90和CEB-FIP MC78模型的计算结果，因为前者计算的管内混凝土收缩值大于后两者。ACI 209R-92模型计算的混凝土和钢管收缩自应力均在表6统计的收缩自应力范围内。

对于收缩引起的钢管应力增大，拱脚截面下弦杆采用本文3种模型计算的自应力分别占收缩总应力的84.2%、82.0%和81.9%；次应力则分别占15.8%、18.0%和18.1%。拱脚截面下弦杆自重作用下钢管和混凝土的应力分别为-92.1 MPa和-13.1 MPa，3种模型计算得到的钢管自应力分别占自重引起应力的23.7%、11.8%和9.3%；次应力则分别占自重应力的4.5%、2.6%和2.1%。从算例来看，管内收缩自应力的影响大于次应力的影响，次应力的影响在结构受力中占的比例不大。考虑徐变对收缩次内力的缓解作用后，次应力会更小；实际桥梁除自重外，还要承受活载等作用。因此，收缩次应力占结构受力的比例会进一步下降，初步设计中可以忽略不计。

温降15 ℃的计算结果大于ACI 209R-92模型，采用该模型计算时可等效降温13.7 ℃。应该指出的是，采用等效降温法计算无法得到收缩自应力值，而收缩自应力远大于收缩次应力。

4 结论与建议

(1)钢管混凝土构件的收缩应变在60 d以前发展较快，60 d时达到180 d总收缩应变的75%以上，在此之后增长较缓，100 d时达到总收缩应变的90%以上，之后趋于稳定；密闭素混凝土构件与钢管混凝土构件的收缩应变规律相似，但钢管混凝土构件180 d收缩应变值比素混凝土构件小22.8%，早期收缩增长速度较素混凝土稍慢。

(2)钢管混凝土收缩变形值与管径相关性小，尺度效应可以忽略，本文的试验结果可推广到较大管径的实际工程应用中。钢管混凝土的收缩变形值随混凝土强度等级的提高而增大，随粉煤灰掺量的增加而减小，随含钢率的增大而减小。本文试验中收缩应变与粉煤灰掺量基本呈线性变化，以掺量0%为基准，粉煤灰掺量为10%、20%、30%和40%的收缩应变分别较其减少6.1%、16.4%、25.5%和34.5%。

(3)ACI 209R-92模型预测钢管混凝土收缩变形值具有较高精度，建议工程使用。对于粉煤灰掺量不大于20%的钢管混凝土构件，可直接使用现有模型。粉煤灰掺量大于20%时预测值偏大，可考虑对其进行修正。本文根据试验结果提出的修正模型，可供参考。

CEB-FIP MC90和CEB-FIP MC78预测钢管混凝土收缩变形值明显偏低，偏于不安全，建议设计计算时不采用。

钢管混凝土收缩变形值变化范围大，等效降温法合理降温较难确定，且该法无法计算占比例较大的收缩自应力，设计计算不建议采用该方法，建议采用收缩模型直接计算。

(4)对一般钢管混凝土拱桥收缩作用进行估算时，可取管内混凝土的收缩应变εc=(172～247)×10-6、钢管混凝土的收缩应变εsc=(78～208)×10-6。对于常用的Q345钢管，管内混凝土收缩产生的钢管应力为16.1～42.8 MPa，达到(4.7%～19.0%)fy，在设计计算中应考虑。钢管混凝土拱的收缩应力中，次应力较小，估算时可以忽略。

参考文献：

[1]韩林海,杨有福,李永进,等.钢管高性能混凝土的水化热和收缩性能研究[J].土木工程学报,2006,39(3):1-9.

HAN Linhai,YANG Youfu,LI Yongjin,et al.Hydration Heat and Shrinkage of High Performance Concrete-filled Steel Tubes[J].China Civil Engineering Journal,2006,39(3):1-9.

[2]王湛,宋兵.钢管高强混凝土自收缩规律的研究[J].建筑结构学报,2002,23(3):32-36.

WANG Zhan,SONG Bing.Research on the Regularity of Autogenous Shrinkage of High Strength Concrete Filled Steel Tube[J].Journal of Building Structures,2002,23(3):32-36.

[3]钟善桐.钢管混凝土结构[M].北京：清华大学出版社,2003.

[4]ICHINOSE L H,WATANABE E,NAKAI H.An Experimental Study on Creep of Concrete Filled Steel Pipes[J].Journal of Constructional Steel Research,2001,57(4):453-466.

[5]TERREY P J,BRADFORD M A,GILBERT R I.Creep and Shrinkage of Concrete in Concrete-filled Circular Steel Tubes[C]//ASCE.Proceedings of 6th International Symposium on Tubular Structures.Melbourne:Rotterdam,1994:293-298.

[6]ICHINOSE L H,WATANABE E,NAKAI H.An Experimental Study on Creep of Concrete Filled Steel Pipes[J].Journal of Constructional Steel Research,2001,57(4):453-466.

[7]UY B.Static Long-Term Effects in Short Concrete-filled Steel Box Columns under Sustained Loading[J].ACI Structural Journal,2001,98(1):96-104.

[8]CHEN B C,SHRESTHA K M.Quantifying Creep of Concrete Filled Steel Tubes[J].Journal of Donghua University:English Edition,2010,27(6):796-805.

[9]中华人民共和国铁道部.TB 10002.1—2005 铁路桥涵设计基本规范[S].北京：中国铁道出版社,2005.

[10]中华人民共和国交通部.JTG D 62—2004 公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京：人民交通出版社,2004.

[11]福建省住房和城乡建设厅.DBJ/T 13-136—2011 钢管混凝土拱桥技术规程[S].2011.

[12]重庆市交通委员会.CQJTG/T D66—2011 公路钢管混凝土拱桥设计规范[S].北京：人民交通出版社,2011.

[13]中华人民共和国住房和城乡建设部.GB 50923—2013 钢管混凝土拱桥技术规范[S].北京：中国计划出版社,2014.

[14]赖秀英,陈宝春.钢管混凝土拱桥收缩次内力计算[J].建筑科学与工程学报,2013,30(3):120-126.

LAI Xiuying,CHEN Baochun.Calculation of Shrinkage Secondary Internal Force of CFST Arch Bridge[J].Journal of Architecture and Civil Engineering,2013,30(3):120-126.

[15]胡曙光,丁庆军.钢管混凝土[M].北京:人民交通出版社,2007.

[16]NEVILLE A M,DILGER W H,BROOKS J J.Creep of Plain and Structural Concrete[M].London and New York:Construction Press,1983:194-199.

[17]ACI Committee 209.Prediction of Creep,Shrinkage and Temperature Effects in Concrete Structures[R].Detroit:ACI,1992.

[18]陈宝春.钢管混凝土拱桥实例集(二)[M].北京：人民交通出版社,2008.

[19]李生勇,李凤芹,陈宝春,等.钢管混凝土拱桥徐变影响分析[J].铁道学报,2011,33(3):100-107.

LI Shengyong,LI Fengqin,CHEN Baochun,et al.Analysis on Creep Effect of Concrete-filled Steel Tubular Arch Bridges[J].Journal of the China Railway Society,2011,33(3):100-107.

[20]中华人民共和国铁道部.TB 10002.3—2005 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].北京：中国铁道出版社,2005.