基于GNSS的列车定位单元设计与性能评估方法

上官伟，袁 敏，肖 杰，蔡伯根，王 剑

(1.北京交通大学 电子信息工程学院，北京 100044； 2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044)

列车定位单元作为列控系统的重要组成部分，能够为列控系统提供当前的列车速度、位置参数。目前列车定位方式主要包括查询应答器、计轴器、卫星导航GNSS等[1]。其中GNSS定位技术，减少了轨旁设备，可以降低列控系统的成本，同时提高列车定位性能，实现不同列控系统的互操作，是未来列车定位的发展趋势[2]。随着列控系统对安全性和可靠性要求的不断提高，列车定位技术也在不断发展，定位方式由单一定位方式发展成为组合定位方式，组合定位利用多种传感器优点，相互补充，弥补了单一传感器定位的不足，提供了高可靠性和高精度的列车定位信息，因此成为一种合理选择。但组合列车定位系统的安全性和可靠性仍有待改进，国内外学者提出利用冗余结构来提高系统安全性和可靠性。一般常用的冗余结构包括三取二结构、二取二结构等。在国外，阿尔斯通、西门子等公司利用这些冗余结构，设计生产了高安全性和可靠性的信号设备，来满足列控系统的需求。

国内也开展了大量基于GNSS的列车定位方案研究工作。文献[3]设计研究了GPS结合地理信息系统GIS的定位方式，并利用GPS数据同电子地图的匹配算法实现列车轨迹数据的估计。文献[4]在INS/GPS 组合导航的基础上，研究了我国INS/北斗组合导航的关键技术。但是目前在国内基于GNSS的列车组合定位技术尚处于研究开发和实验验证阶段，研究内容一般都侧重于实现系统的某些功能，而对于极为重要的可靠性和安全性问题，尚没有成熟、系统的研究成果。针对这一现状，本文设计了一个采用冗余结构的基于GNSS的列车组合定位单元，并对其性能进行评估。针对性能中重要的两个参数可靠性和安全性评估方法进行了探索性研究，对促进新型列控系统发展，提高列车运行安全水平及效率，降低运营成本具有重大意义。

1 基于GNSS的列车定位单元设计

本文设计的基于GNSS的列车定位单元适用于低密度线路，以提高列车安全运行水平、减少轨旁设备、降低运营维护成本为目标，拟实现的主要功能为：从传感器采集速度位置信息后进行数据融合和处理，为车载主机输出可靠的列车定位信息。定位信息包括正常速度、最大速度、最小速度、加速度等信息。系统性能需要满足以下可靠性和安全性需求。

(1)RAM需求见表1。

表1 RAM需求

(2)基于GNSS的定位单元应当遵循的可靠性、可用性、可维护性设计原则要求见表2。

表2 RAM设计原则

(3)定位单元的安全性指标要求为：危险侧故障率THR(Tolerable Hazard Rate)≤10-6/h(THR源于EN标准，用来衡量SIL等级，等同于IEC 61508高要求或连续操作模式下的PFH，THR≤10-6/h为SIL2所要求的安全性指标)。安全性设计原则见表3。

表3 安全性设计原则

整个定位单元由逻辑处理单元和多种类型的定位传感器单元组成，并采用二取二冗余结构进行系统设计。如图1所示，两套独立的系统采集到数据后分别输入到两个逻辑处理单元进行处理。每个逻辑处理单元比较两个输入是否一致，若输入一致则进行处理，否则判定定位单元故障。对两个逻辑处理单元的输出进行比较，输出结果一致则输出到车载主机，否则切断输出。定位传感器单元包括速度传感器ODO(Odometer)、惯性测量单元IMU(Inertial Measurement Unit)和基于全球导航的卫星系统GNSS。逻辑处理单元负责传感器信息的融合处理、地图匹配、定位结果输出等功能。基于GNSS的定位单元对外接口采用兼容性设计，可直接替换既有列控系统中使用的定位单元SDU(Speed & Distance Unit)，与车载主机通过总线相连接。

为实现定位单元架构设计，将基于GNSS的定位单元采用模块化设计划分为安全电源板(2块)、通信板(1块)、输入板(2块)、逻辑板(2块)和输出板(1块)。为最大限度地缩小体积、提高系统电磁兼容性、便于插拔，各单板采用刀片式的结构设计，并依次排列固定在一个机笼里，板间通过背板相互连接。单板前面板有开孔，供定位单元与外部传感器、维护调试设备、车载主机连接使用。每个单板上同时还设有指示灯，便于及时查看各板的运行状态，快速判断定位单元是否正常工作。图2为基于GNSS的列车定位单元前视图。

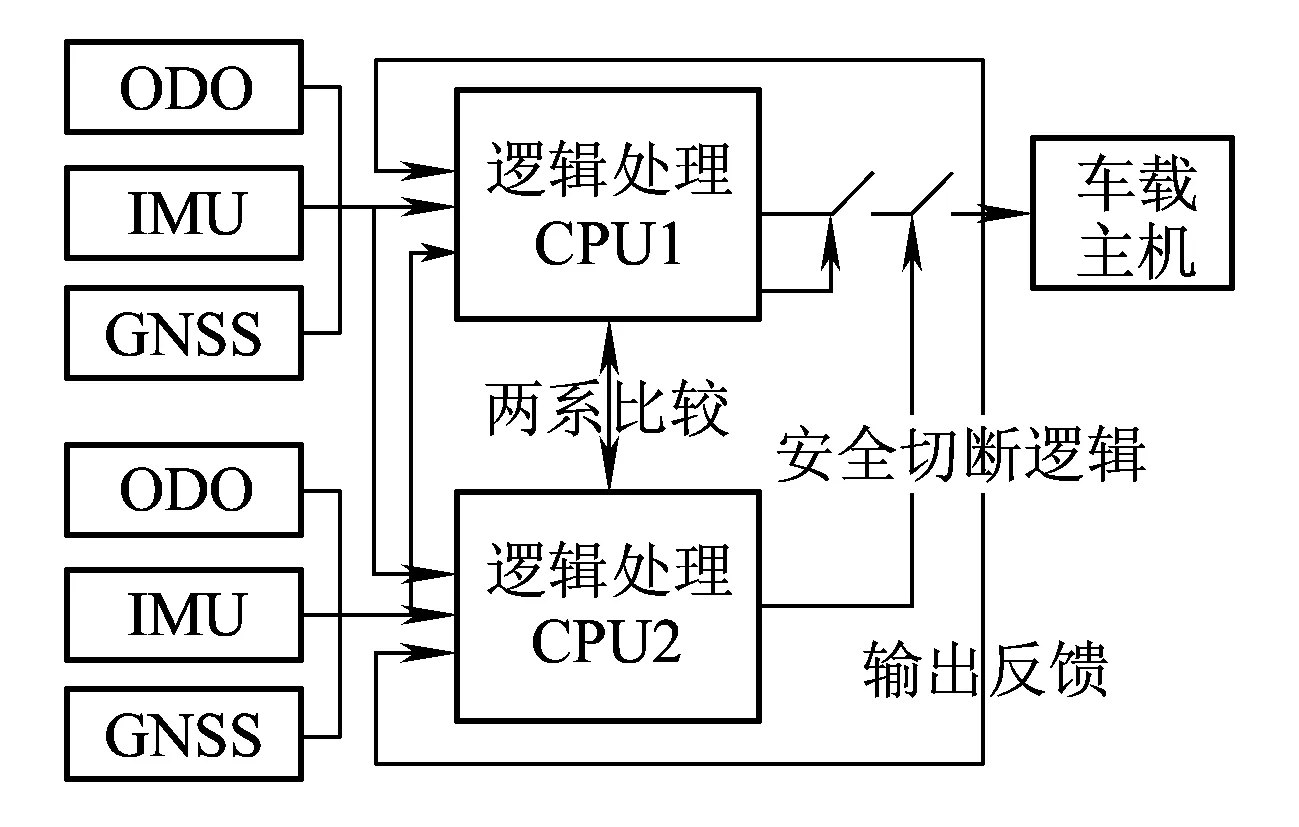
图1 基于GNSS的定位单元逻辑框图

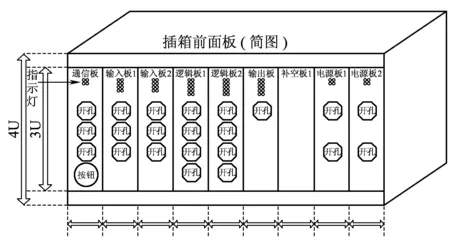
图2 基于GNSS的列车定位单元前视图

设计好列车定位单元后，对其进行可靠性、安全性和功能验证。一方面研究系统发挥功能的能力及无故障运行时间，另一方面研究系统发生危险故障的概率，综合评价定位单元的硬件性能，对定位单元进行功能验证，评估系统实际的功能表现。

列车定位单元各系统板的内部结构如图3所示。

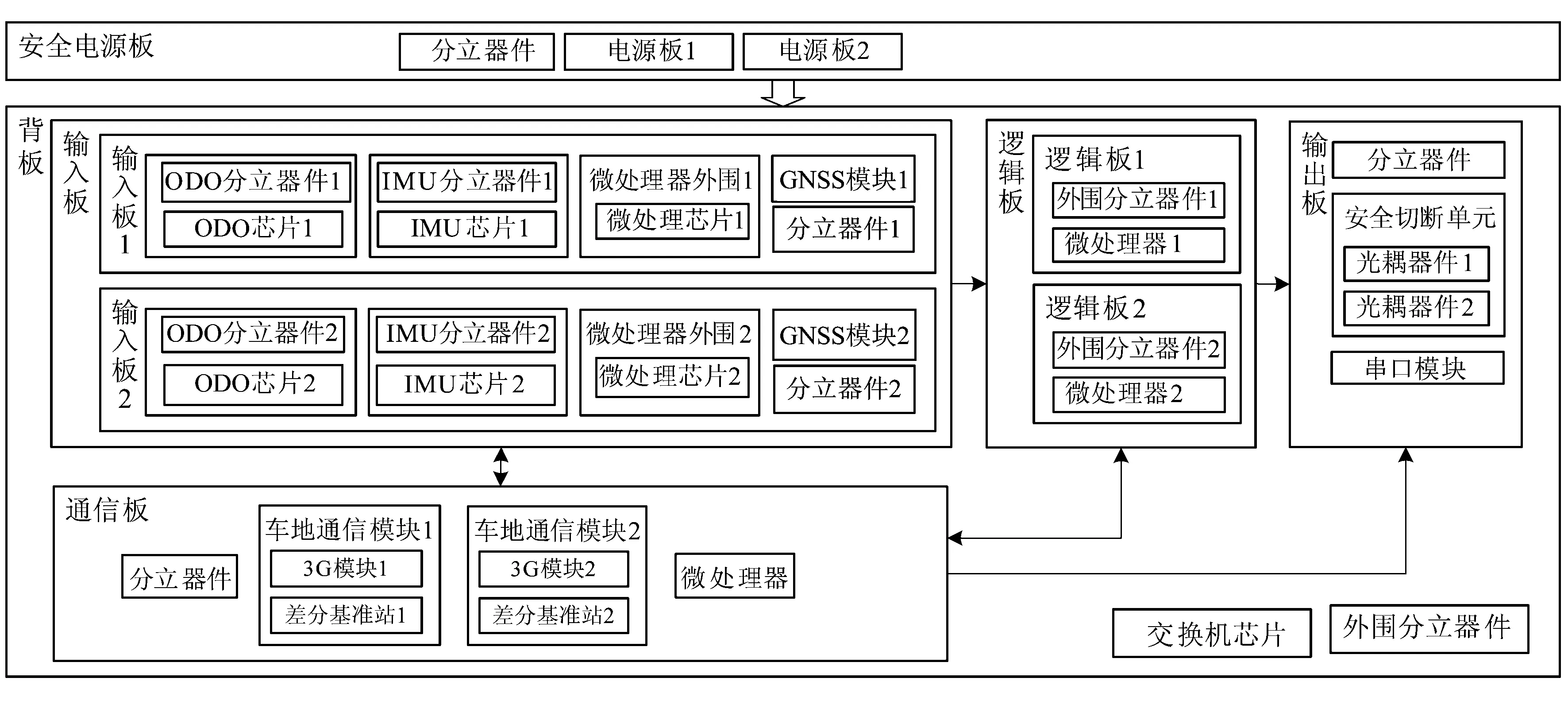
图3 基于GNNS的列车定位单元结构图

2 基于GNSS的列车定位单元可靠性分析与评估

本文对定位单元的可靠性分析采用故障树分析FTA(Fault Tree Analysis)方法[5-8]。在故障树分析中，系统故障树的建立是关键。只有完善度高的故障树，才能够准确进行定性、定量分析，分析结果才具有实用性。在本文中以无法完成列车定位为顶事件，分析可能导致顶事件发生的因素，逐层向下分析，建立GNSS列车定位单元的故障树如图4所示。

2.1 可靠性定性计算及分析

根据建立好的故障树进行定性分析，即求其最小割集。导致顶事件发生的各底事件组合成为割集，这种最低限度的底事件组合称为最小割集，它是顶事件发生的充要条件，有多少个割集，顶事件就有多少种发生的可能。根据建立的基于GNSS定位单元的故障树，利用下行法求故障树割集，并找到故障树的最小割集。

下行法的基本思路是由顶事件逐级向下[9]，用每个逻辑门输入的基本事件置换各门的输出，直到输入都是基本事件为止。这种算法的原理是：将或门的输入事件排成不同的行(增加割集的数量)，将与门的输入事件排在同一行(增加一个割集的容量)，根据矩阵的最后一列，得到系统的所有割集。然后逐一判断每个割集是否为最小割集。最终得到的定位单元有32个最小割集，分别为{E1}、{E2，E3}、{E4}、{E5}、{E6}、{E7，E9}、{E7，E10}、{E8，E9}、{E8，E10}、{E11}、{E12}、{E13}、{E14，E16}、{E15，E16}、{E14，E17}、{E15，E17}、{E18}、{E19}、{E20}、{E21}、{E22}、{E23}、{E24}、{E25}、{E26}、{E27}、{E28}、{E29}、{E30}、{E31}、{E32}、{E33}。

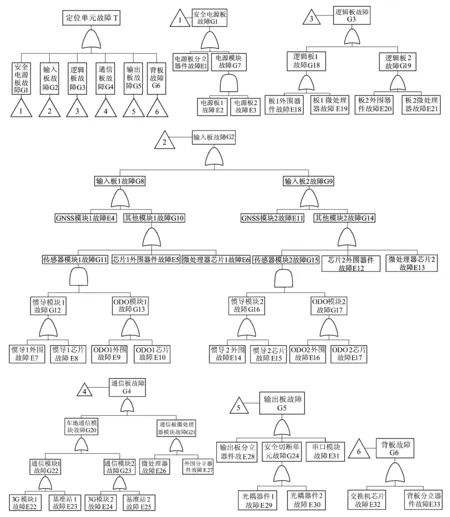
图4 基于GNSS的列车定位单元故障树

2.2 可靠性定量计算及分析

故障树的定量分析内容主要包括[10]：系统失效概率；底事件的重要度。根据重要度的大小依次排序得到最佳的故障诊断和器件修理顺序。

2.2.1 系统失效率

(1)最小割集不相交的计算方法

不相交是指在很短的一个时间内，同时发生两个、两个以上最小割集的概率是零，且在各个最小割集里不会出现重复的底事件。此时有

( 1 )

式中：Fs(t)为系统的失效概率；Φ(X)为底事件X的结构函数；Kj为第j个最小割集；Fi(t)为第i个底事件的失效概率。

假设系统最小割集不相交，则顶事件发生的概率，即系统失效率为

P(t)=Ptop(t)=(1-e-λx1t)+

(1-e-λx2t)(1-e-λx3t)+…(1-e-λx31t)+

(1-e-λx32t)+(1-e-λx33t)

( 2 )

式中：Ptop(t)为顶事件发生的概率；λxi为底事件xi的失效率。

基于对系统失效的分析，也可以计算出其他参数，即系统的可靠度为

R(t)=1-Ptop(t)=1-F(t)

( 3 )

(2)最小割集相交的计算方法

在系统失效发生的最小割集中，由于同一个底事件在几个最小割集中多次重复出现，即最小割集之间是相容的。顶事件可以表示为

T=C1+C2+C3+…+Cn

( 4 )

式中：Ci为最小割集。则顶事件发生的概率为

(-1)n-1P(C1C2…Cn)

( 5 )

式中：Ci、Cj、Ck分别为第i、j、k个最小割集。基于GNSS的定位单元最小割集有32个，其中有4组割集存在相交情况，因此结合式( 2 )和式( 5 )计算顶事件发生的概率，这样避免了近似计算，防止在求解失效密度时带来不确定因素。

根据以上分析，将基于GNSS的定位单元故障树中的底事件发生概率参数(即失效率)代入相应公式中，得到定位单元故障率如图5所示。

图5 基于系统故障树-顶事件发生概率

如图5所示，t=24 h，顶事件发生的概率为0.02%；t=720 h，顶事件发生的概率为0.07%；t=8 760 h，顶事件发生的概率为17.84%；t=80 000 h，顶事件发生的概率为99.72%。如果要保持基于GNSS的定位单元正常输出，定位结果的概率为99.27%，则每隔3个月对系统进行一次维修、检查最合理。

由系统的失效公式，同样可推导出系统的可靠度以及失效概率密度函数。系统的失效概率密度函数为

fsystem(t)=P′(t)

( 6 )

图6为定位单元失效概率密度函数-时间曲线图，可以看出失效密度曲线在6 800 h内处于增长状态，导致在该时间段内定位单元故障率呈现快速增长状态。随着系统失效密度函数逐步下降，系统的故障率上升速度减慢并最终趋于稳定状态。

图6 系统失效密度函数仿真图

2.2.2 重要度计算

除了计算故障树顶事件(定位单元无法完成定位功能)发生概率和系统可靠度等参数以外，更重要的是利用故障树计算各底事件的重要度。重要度代表了单个部件或者最小割集对顶事件发生的影响程度，在类似于基于GNSS的定位单元这样的大型、复杂系统中，计算底事件重要度能够确定系统关键部件，改善系统设计。

(1)概率重要度计算

底事件概率的变化率对系统概率变化影响的程度称为底事件的概率重要度，其计算公式为[11]

( 7 )

式中：Ipr(j)为第j个底事件的概率重要度；Q为系统失效概率；qj为第j个底事件的失效概率。

由于底事件的概率重要度差异较大，根据计算结果，将底事件概率重要度处于同一数量级的划分为一组，并进行对比，定位单元各底事件概率重要度如图7所示。

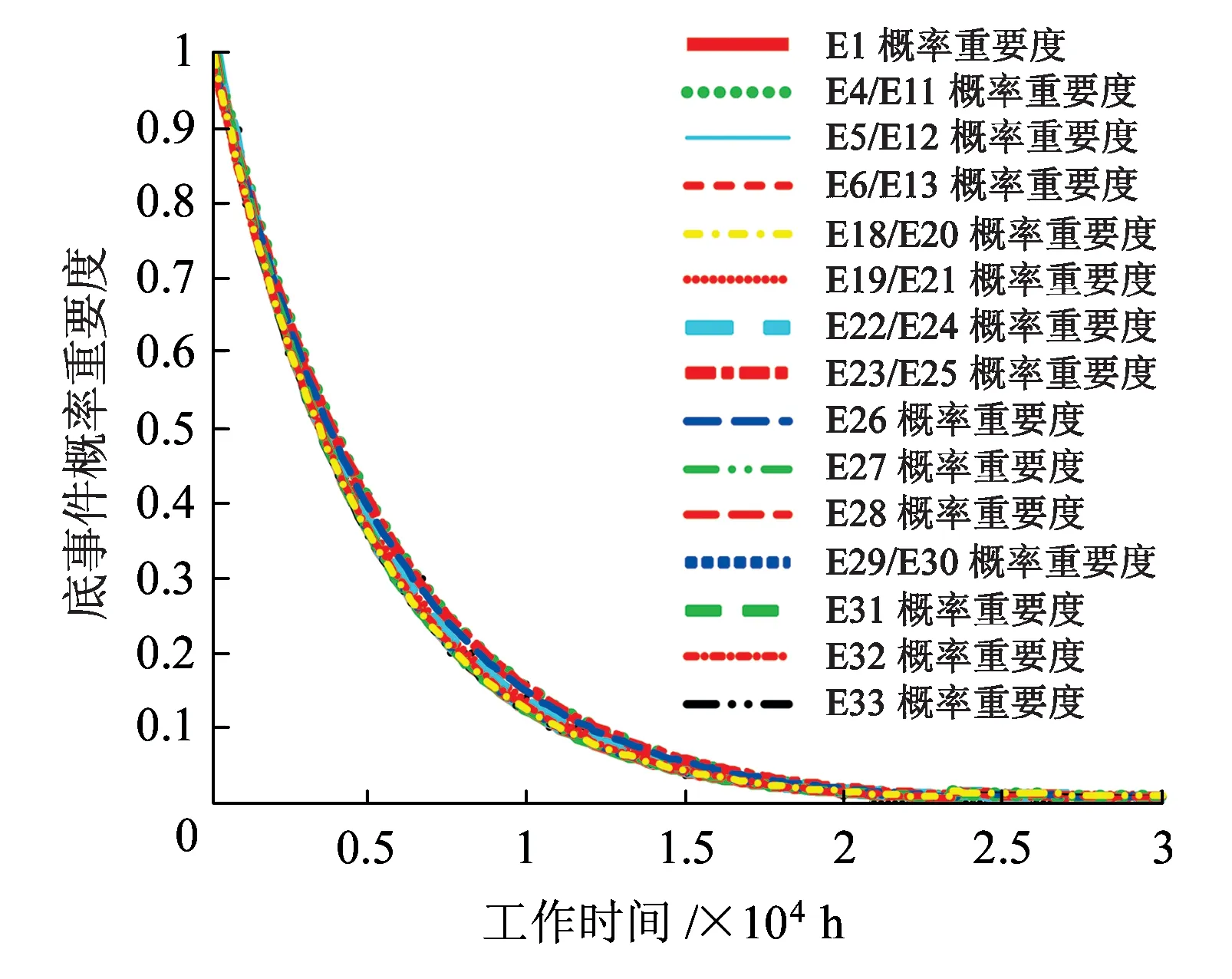
(a)底事件概率重要度函数(1)

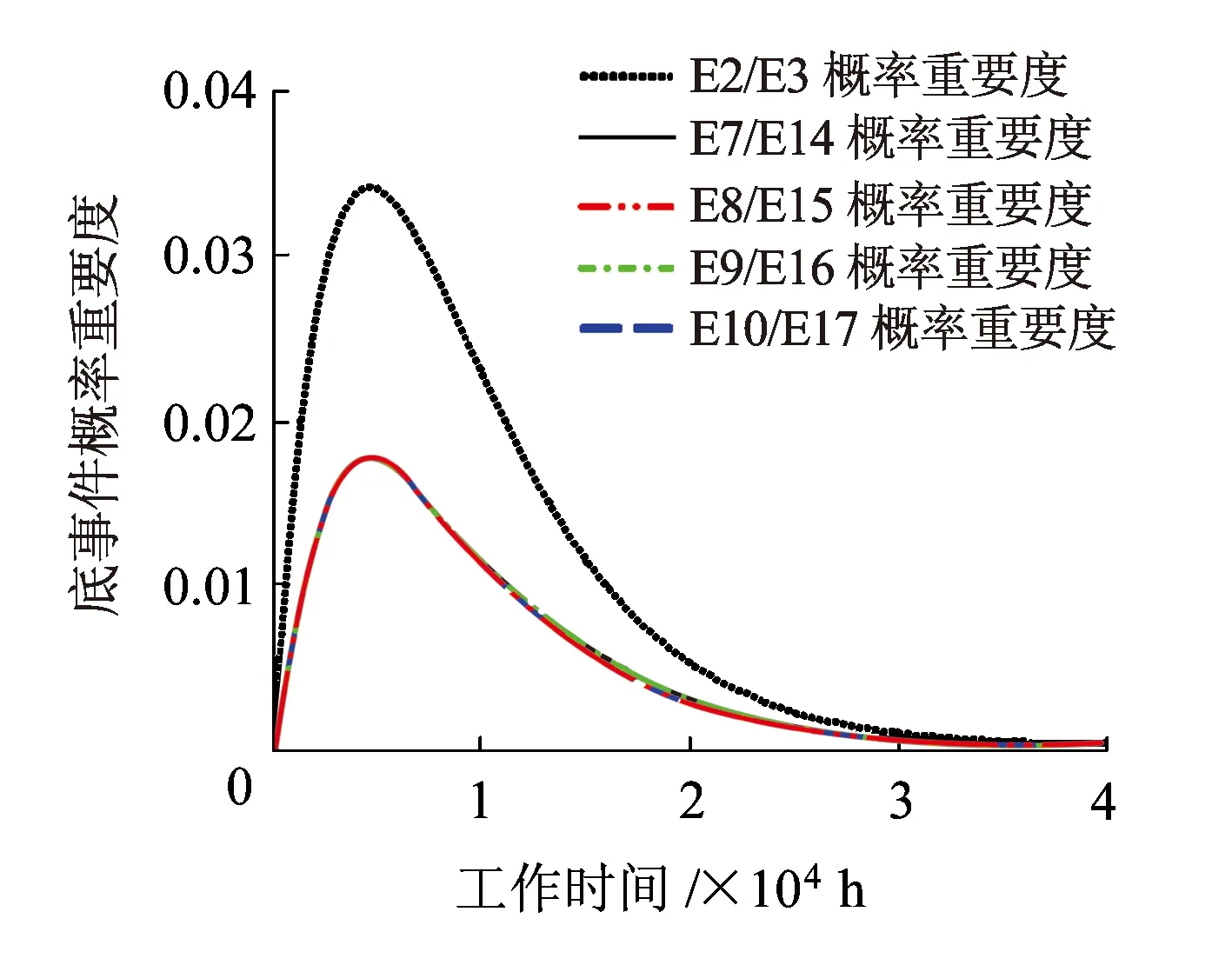
(b)底事件概率重要度函数(2)图7 底事件概率重要度函数

(2)结构重要度Ist(j)计算

底事件的结构重要度表示各底事件在故障树结构中的重要度。此量值与该底事件的发生概率大小无关。Ist(j)=0的底事件与顶事件无关，应予以删除。Ist(j)越接近1的底事件在结构上越重要，因此设计时应尽量提高它的可靠性，计算公式为

( 8 )

式中：Ist(j)为第j个底事件的结构重要度；n为系统全部底事件的个数；nj为将j底事件加入2n-1个组合中后，使该组合由非割集变成割集。2n-1个组合由真值表求得。

根据式( 8 )，得到定位单元各底事件结构重要度如图8所示。

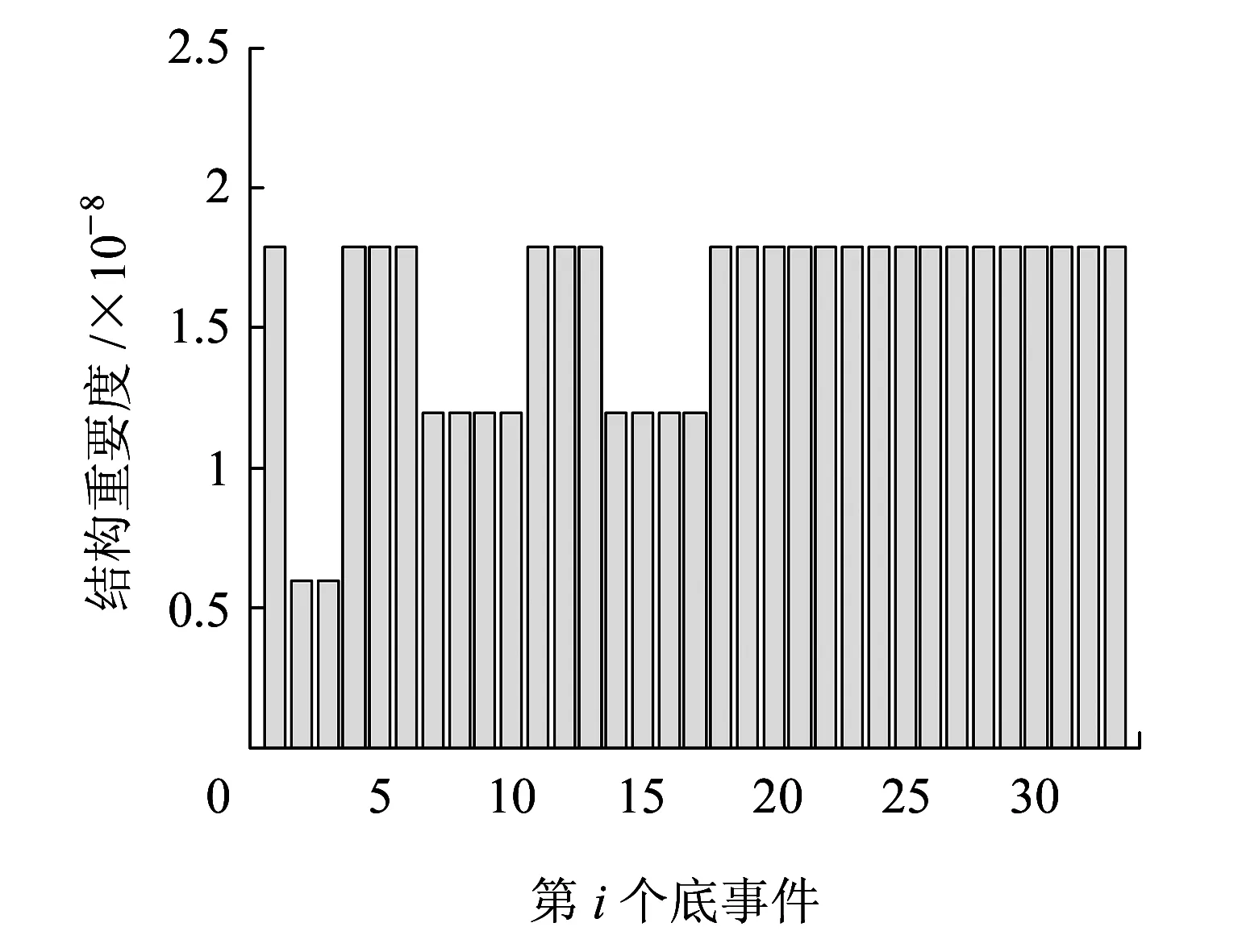
图8 系统结构重要度

图9 综合改进后系统可靠性变化

从图9可以看出，提高多个概率重要度和结构重要度较高部件(E19、E20、E24、E26、E27、E28等)的可靠性时，整个定位单元可靠性明显提高。满足了定位单元可靠性指标需求。

3 基于GNSS的列车定位单元安全性指标计算与评估

安全完整性等级作为安全相关系统的安全性评价指标，是分析和评价系统安全性的重要依据，也为改进系统安全性提供指导，分为硬件安全完整性和系统安全完整性两大类。系统安全完整性是不可定量的部分，它是生命周期各阶段人为因素导致的，包括设计错误、操作错误、生产错误等。硬件安全完整性受限于结构约束和随机硬件失效。随机硬件失效是指随机发生的、由于硬件元器件老化或损坏造成的故障。评价随机硬件失效的指标为高要求或连续操作模式下的每小时危险失效概率PFH。PDS方法由挪威工业科技研究院SINTEF开发，用于定量计算PFH。该方法同新版IEC 61508中计算PFH的方法理念一致，且更加注重共因故障的考虑，因此PDS方法广泛应用于石油等工业行业的系统安全性评估。本文采用PDS方法计算定位单元的PFH。

3.1 PDS的共因故障模型

为了提高基于GNSS定位单元的安全性能，本文引入了冗余结构，传统定量计算冗余系统安全性时，通常假设每个单元失效都是互相独立的，但是冗余系统中一般都存在共因故障，由于相同的原因，而导致了一个及一个以上的模块或者设备失效。例如，在高温环境下，若冷却风扇失效，就会导致两个冗余逻辑控制器同时失效，使得冗余系统的可靠性和可用性降低。

共因失效率与系统结构相关，系统通道数不同，则相应的共因失效率也不同。例如3通道系统，其中2个通道共因失效，第3个通道则不一定发生失效，它发生共因失效的概率可能只有30%，也就是说3个通道的共因失效率小于2个通道的共因失效率，不同的表决系统，共因失效率不同。PDS方法里由N个相同模块组成的MooN冗余结构的共因故障率为

PFHMooN=CMooNβλ

( 9 )

式中：CMooN为配置因子；λ为每个模块的失效率；β为任何两个冗余模块的共因故障发生概率；MooN为表决结构，表示至少有M个单元故障，则表决单元故障。CMooN参考值见表4[12]，然而CMooN的值并非恒定的，而是与实际系统的特性有关，想要更加精确地表示系统的共因故障，就需要根据实际系统合理选择CMooN值。

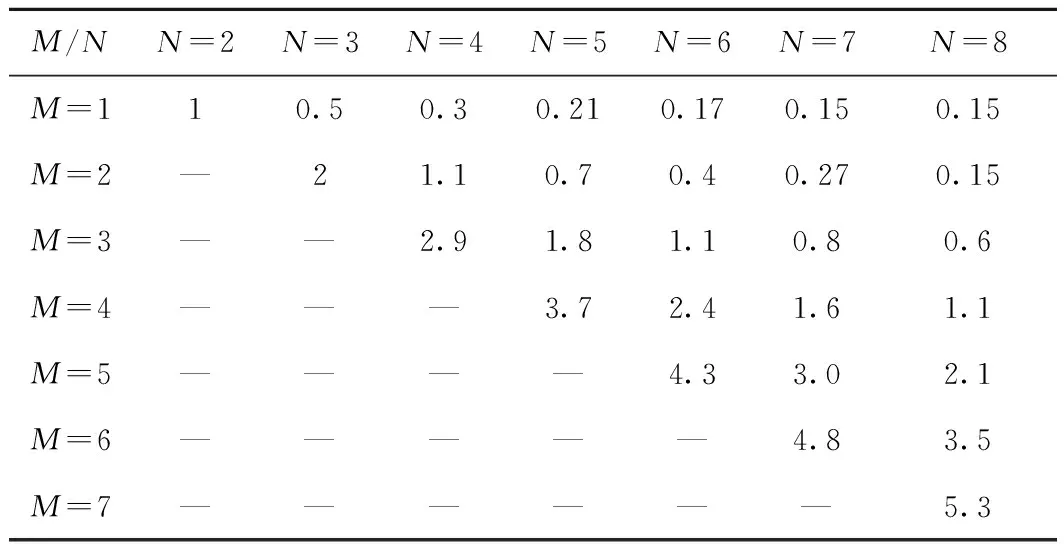
表4 不同表决逻辑的CMooN因子

冗余结构的PFH包括独立故障部分PFH(ind)(Independent Failures，ind)和共因故障部分PFH(CCF)(Common Cause Failures，CCF)，表5中给出的是冗余模块间的失效率等参数完全一致时的PFH计算公式，但实际情况下，冗余结构中各模块未被检测到的危险失效率λDU以及功能测试间隔时间τ可能不同，这时若要继续利用表5中的计算公式，就需要做如下处理。

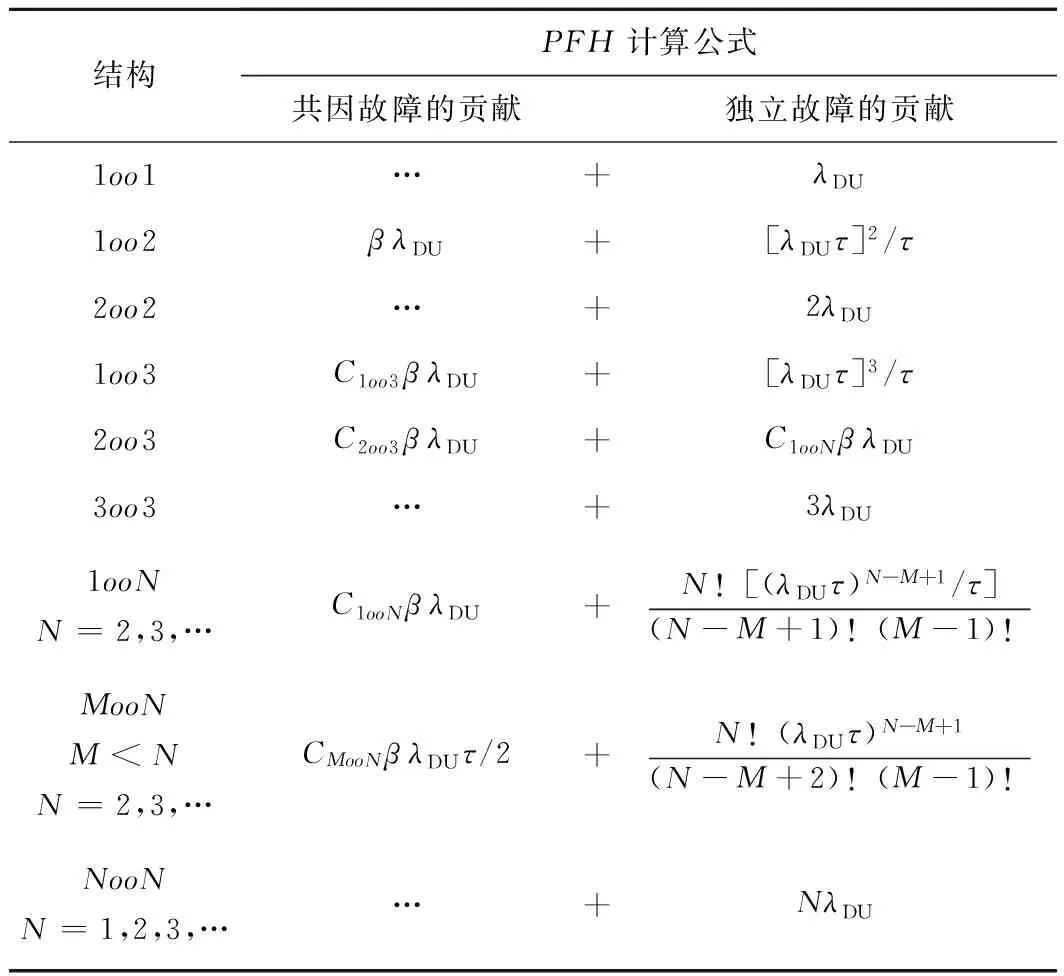
表5 PFH计算公式

以N模块为例，假设每个模块λDU均不同，用λDU，i来表示，i=1，2，…，n，则整个系统的λDU为

(10)

整个系统的功能测试间隔时间τ取各模块功能测试间隔时间的算数平均值，以N模块为例，则

(11)

式中：τi为第i个模块的功能测试间隔时间。

系统独立故障部分PFH(ind)以1ooN表决结构为例，其计算公式为

PFH1ooN=(λDUτ)N/τ+(λDDτ1)N/τ1

(12)

式中：τ为功能测试间隔时间；τ1为诊断测试间隔时间；λDU为未被检测到的危险失效率；λDD为被检测到的危险失效率。在铁路系统应用中，诊断测试间隔时间通常很短，其对于系统PFH值的贡献可以忽略。

3.2 基于GNSS的定位单元安全完整性评估

基于GNSS列车定位单元的组成器件较多，各器件的安全完整性分析方法相似，所以本文以输入板为例，介绍安全完整性定量计算方法。冗余结构的存在导致输入板的可靠性框图非常复杂(如图10所示)，这时可将其看成一个复杂的系统，继续划分为若干个相对独立的模块分别求解。焊接点和印制板的共因故障将导致整个输入板故障，所以代表焊接点和印制板共因故障的灰色模块直接串联在输入板可靠性框图RBD(Reliability Block Diagram)中，而GNSS模块及其他两个传感器之间的共因故障则只能导致该类型传感器故障，其他传感器仍将正常工作，因此不能直接串联在输入板可靠性框图中。

输入板的PFH计算公式为

PFHsrb=PFHGNSS·[(PFHIMU·τ+

PFHODO·τ)2/τ+PFHwclq]+PFHdlb

(13)

在计算过程中，诊断覆盖率DC(Diagnostic Coverage)的取值和所采用的IEC 61508中推荐的诊断技术有关，通常认为电阻、电容等简单电子器件的诊断覆盖率可取99%，焊接点、印制板诊断率作为接插件，只要保证工艺水平同样可取99%，微处理器、复杂电路组成的模块单元等因为结构复杂，故障模式难以被全部侦测，为保证计算的可信度，通常取其诊断覆盖率为90%，以上取值组合称为合理推断值。

根据铁路信号系统的特征，功能测试间隔时间τ取典型值24 h。β因子可以根据IEC 61508中的表格填表得到，通常取值范围为0～0.25。

本文假设元器件所有故障的50%为危险侧故障。诊断覆盖率DC分别取0.99、合理推断值、0.9，定位单元的随机硬件失效安全完整性等级随β的变化曲线如图11所示。从图11可以看出诊断覆盖率取“合理推断值”得到整个定位单元的随机硬件失效安全完整性等级均为SIL2，这表明定位单元的设计符合安全需求指标“危险侧故障率THR≤10-6/h”的要求。同时也表明诊断覆盖率的选取对系统安全性有着重要影响，在系统设备可靠性难以提高的情况下，提高其诊断覆盖率也是提高系统安全性的有效手段。

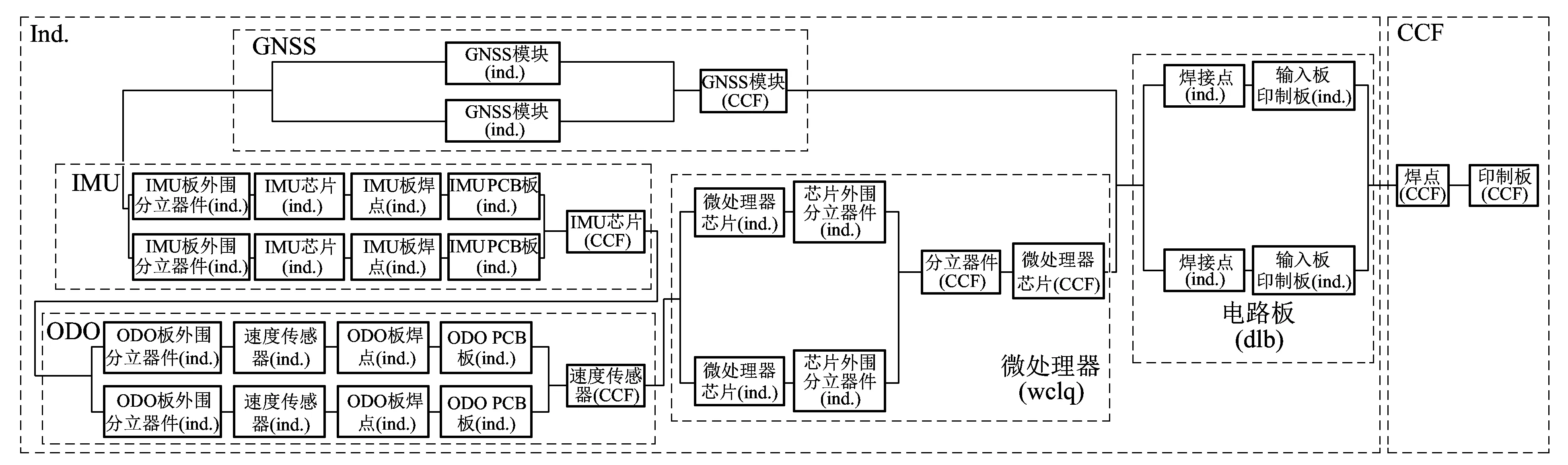
图10 输入板的可靠性框图

图11 定位单元PFH值

在系统的安全性满足安全指标需求的情况下，为了提高系统的安全性，本文做了进一步的研究。通过计算各板的PFH值，得到定位单元硬件安全完整性较低的单板为：电源板、通信板。为了直观的表示随机硬件失效安全完整性较低的单板对整个定位单元随机硬件失效安全完整性的影响，将PFH值较低的电源板、通信板、背板的PFH值相加，与其余单板的PFH值加和进行对比，如图12所示。可以看出电源板、通信板、背板三块板的PFH加和已经将系统SIL拉低至SIL2，而输入板、输出板、逻辑板SIL加和对系统SIL影响不大(如图13所示)。显然，改进电源板、通信板、背板的安全性有利于系统安全完整性等级的提升，这为将来提高系统整体安全性提供了理论依据。

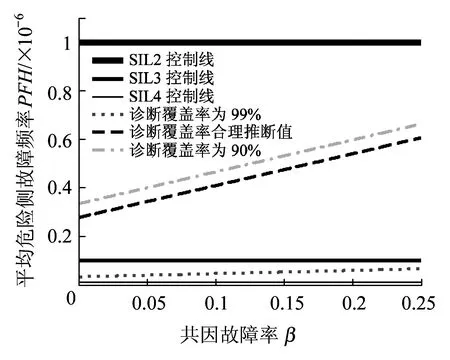
图12 电源板、通信板、背板SIL加和

图13 输入板、输出板、逻辑板SIL加和

4 基于GNSS的列车定位单元功能验证与评估

对设计好的定位单元进行系统功能验证，将定位单元装载到汽车上，在北京市海淀区的一段公路上进行现场测试。测试时，驾驶人员驾驶车辆沿公路行驶。图14是设计完成的列车定位单元。

图14 列车定位单元的实物图

借助地图数据采集软件，采集输出板的原始数据，并在MATLAB软件中进行仿真，显示的地图模型如图15所示。

利用地图匹配软件比较定位数据和基准点，如图16所示，在地图上显示了列车定位单元输出的线路数据和地图匹配软件输出的基准线路数据。可以看到列车定位单元定位的线路数据与实际的线路数据拟合得较好，但还存在一定的误差。

图15 仿真的地图模型

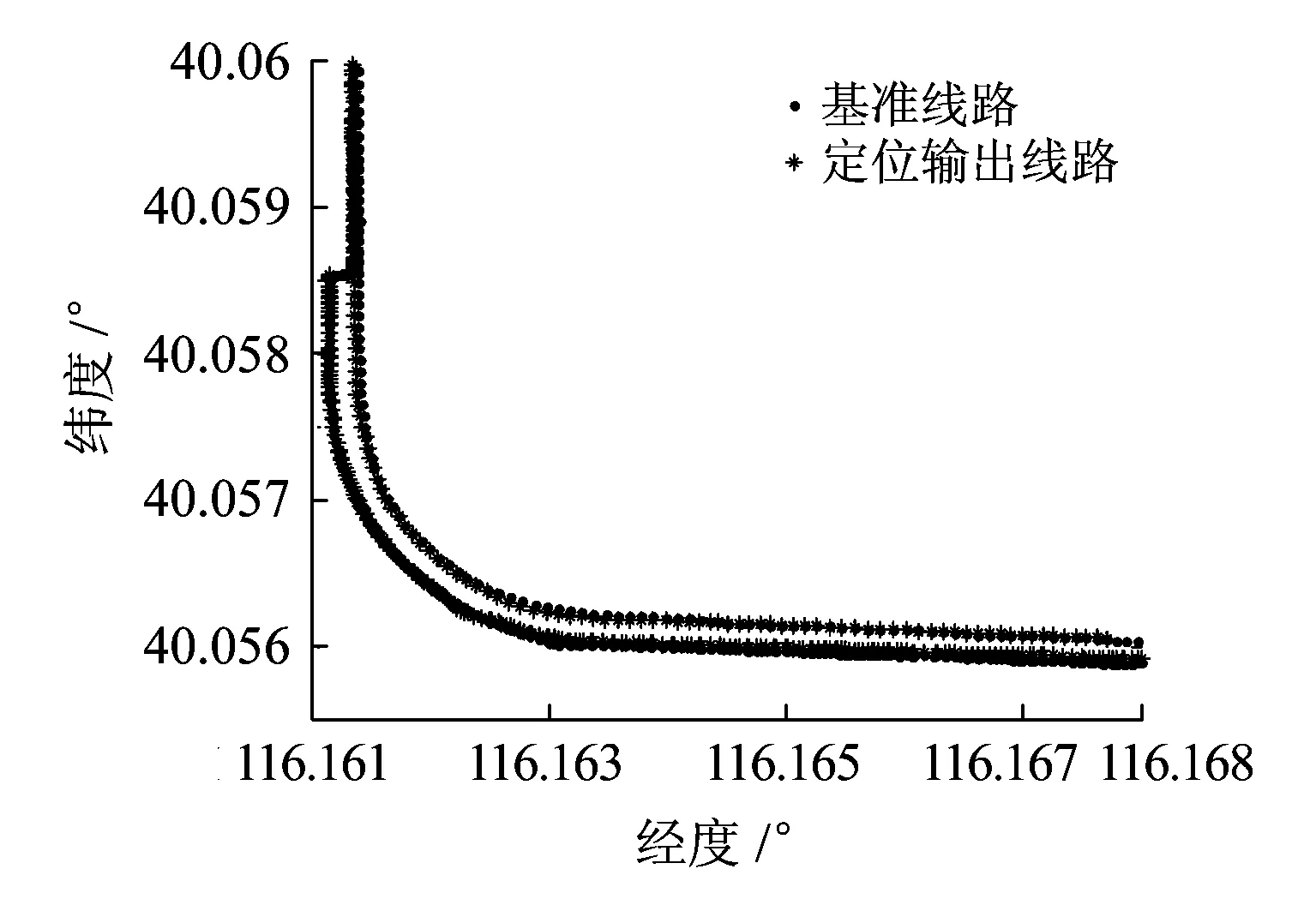
图16 实际的地图模型

通过数据分析，计算得到平均误差为1.885 m，方差为1.804 4 m。定位精度满足了铁路上的定位要求。因为本次实验是在公路上进行的，公路相较于铁路，道路情况复杂、道路较宽且不规则、路上绿化遮挡多等多个因素影响了定位的精确性，所以实际在铁路上的定位效果要好于在公路上的定位。

本次实验结果显示列车定位单元能可靠地工作，并且定位精度满足铁路的定位要求。

5 结束语

列车定位单元作为列控系统的重要组成部分，提供列车速度、位置信息，确保列控系统正常工作和安全运行，实现列车超速防护等安全相关功能。随着铁路快速发展，列控技术逐步从固定闭塞向移动闭塞发展，这对定位单元的定位精度以及系统性能提出了更高的要求。

本文采用模块化设计方式将定位单元划分为安全电源板(2块)、通信板(1块)、输入板(2块)、逻辑板(2块)和输出板(1块)。采用故障树理论对设计的基于GNSS的定位单元可靠性进行研究。以定位单元无法完成定位功能为顶事件建立系统故障树，对其进行定性和定量分析。定性分析求得基于GNSS的列车定位单元总共有32个最小割集，说明导致顶事件发生就有32种可能。定量分析包括两个方面，一方面是计算顶事件发生概率等可靠性基本参数，计算结果表明所设计的定位单元可靠性满足需求指标的要求，即系统一个月内发生故障的概率<1‰；另一方面是对故障树各底事件的重要度进行分析，通过计算底事件概率重要度和结构重要度，确定了影响系统可靠性的关键部件，为进一步优化系统可靠性提供了依据。对于定位单元的安全完整性评价，采用了PDS方法对其硬件SIL中的PFH指标进行定量计算。计算结果表明定位单元的系统板硬件满足SIL2的要求。通过进一步的子系统安全完整性分析，确定了对定位单元安全完整性影响较大的模块。通过对列车定位单元的可靠性和安全性分析，全面评价了设计的列车定位单元系统性能。最后对设计的列车定位单元进行功能验证，结果显示定位单元能可靠定位，定位误差在2 m内，可以满足定位要求。

参考文献：

[1]陈韶霞，孙永明，刘立月.基于GNSS的高速列车多传感器组合定位方法研究[J].河北省科学院学报，2011，28(1)：31-34.

CHEN Shaoxia,SUN Yongming,LIU Liyue.Research about High-speed Train Multi-sensors Information Fusion Location Method Based on GNSS[J].Journal of the Hebei Academy of Sciences,2011,28(1):31-34.

[2]王剑.基于GNSS的列车定位方法研究[D].北京：北京交通大学,2007.

[3]李睿.基于GPS和GIS的列车定位系统研究[J].铁道通信信号,2006,12(4):60-61.

LI Rui.Research of Train Location System Based on GPS and GIS[J].Railway Signalling & Communication,2006,12(4):60-61.

[4]蒋庆仙.北斗/INS组合导航关键技术分析[J].全球定位系统,2006,20(6):56-62.

JIANG Qingxian.The Crucial Technologies in INS/BD Integrated Navigation System[J].GNSS World of China,2006,20(6):56-62.

[5]MARRADI L,GALIMBERTI A,FOGLIA L,et al.GNSS for Enhanced Odometry:the GRAIL-2 Results[C]//Workshop on Satellite Navigation Technologies & European Workshop on Gnss Signals & Signal Processing.New York:IEEE Press,2012:1-7.

[6]朱继洲.故障树原理和应用[M].西安：西安交通大学出版社,1989.

[7]XIANG J,FUTATSUGI K,HE Y.Fault Tree and Formal Methods in System Safety Analysis[C]//The Fourth International Conference on Computer and information Technology.New York:IEEE Press,2004:1 108-1 115.

[8]ZAMPINO E J.Application of Fault-tree Analysis to Troubleshooting the NASA GRC Icing Research Tunnel[C]//Symposium on Reliability and Maintainability,2001:16-22.

[9]季慧媛.动态故障树分析方法研究[D].北京：国防科学技术大学,2002.

[10]邵延峰，薛红军.故障树分析法在系统故障诊断中的应用[J].中国制造业信息化,2007,36(1):72-74.

SHAO Yanfeng,XUE Hongjun.Application of Fault Tree Analysis in Fault Diagnosis[J].Manufacturing Information Engineering of China,2007,36(1):72-74.

[11]韩明.FTA法和重要度分析在某系统可靠性中的应用[J].运筹与管理,2000,9(1):58-61.

HAN Ming.FTA Method and Importance Analysis in System Preliability[J].Opertations Research and Management,2000,9(1):58-61.

[12]HOKATAD P,HABREKKE S,LUNDTEIGEN M A,et al.Use of the PDS Method for Railway Applications[R].SINTEF Technology and Society,2009.