基于前景理论的铁路应急预案多指标风险评估研究

常建鹏，陈振颂，2，周国华，李延来，2

(1.西南交通大学 交通运输与物流学院，四川 成都 610031；2.西南交通大学 综合交通运输智能化国家地方联合工程实验室，四川 成都 610031；3.西南交通大学 经济管理学院，四川 成都 610031)

铁路应急管理理论研究在我国尚处于起步阶段，然而，近年来在理论探究及具体实践方面均取得了一定的进展，已形成一个相对独立的研究领域。目前我国已基本建立了以“一案三制”为核心的铁路应急管理体系，即铁路应急预案、铁路应急管理体制、铁路应急管理机制、铁路应急管理法制四个部分[1]。在保障铁路运输安全及秩序、减少或避免突发事件的发生、降低人员伤亡及财产损失等方面起着重要作用。而铁路应急预案评估研究作为铁路应急管理体系的重要组成部分，已得到了众多学者的重视。通过应急预案的评估，可全面考量预案的编制质量、实施过程和效果，也可在此基础上形成反馈信息，为预案的修正、调整提出有针对性的建议，从而提高预案的科学性与可操作性。

目前，已有学者通过构建评估指标体系，并采用改进层次分析法[2，3]、改进DEA法[4]、案例推理法[5]、多属性决策方法[6]等对铁路应急预案展开评估。实际上，铁路突发事件种类繁多，其严重程度与影响范围会有所不同，须根据应急场景的具体情况确定所需启动预案的类型，以便于相关人员有针对性地应对和处置突发事件。为此，应急预案根据突发事件的类型、事故后果的严重程度以及预案的面向对象等划分为不同的类型，如站段级行车事故应急处置方案、铁路局级破坏性地震应急预案、部级突发公共事件总体应急预案等。评估专家在对某类铁路应急预案进行评估时，由于其自身知识的局限性以及所掌握信息的有限性，很难完全确定该预案能否有效地应对相应的突发事件，但可给出若采用该预案后将要出现的各种可能情况，亦可根据统计资料和调研分析预测出各种情况出现的概率，因而铁路应急预案评估是风险决策问题。然而，现有针对铁路应急预案评估的研究并未考虑风险因素，故将风险因素纳入应急预案评估过程的考量具有重要意义。

当前，已有较多关于风险决策的研究，但多数研究建立在决策者是完全理性的假设基础之上，却较少考虑到决策者的实际心理行为因素。事实上，决策者面临风险决策时，往往有如参照点依赖、损失规避、敏感性递减和概率判断扭曲等心理特征[7]。需要指出的是，文献[8，9]提出的前景理论将决策者的非理性因素纳入到决策过程中，能更加准确描述决策者在风险环境下的心理行为特征。目前，基于前景理论的风险决策研究已有一定进展，如文献[10]提出基于梯形模糊数和前景理论的交互式多准则决策方法，文献[11]提出基于累积前景理论和Choquet积分的多属性风险决策方法，文献[12]提出基于前景ITFNCI算子的群体MULTIMOORA决策方法解决多方参与且决策者信息关联的多属性风险群决策问题。

事实上，铁路应急预案评估即是铁路管理部门组织相关专家运用科学的方法，按照一定的程序，对应急预案的各个方面展开评估的过程。然而，现有研究除风险因素外，还较少考虑其他各类复杂性因素。一方面，由于铁路突发事件涉及面广、决策复杂，预案评估需要充分集结各方面专家的意见。另一方面，由于实际问题的复杂性以及各专家在认知角度、知识水平等方面存在的差异性，评估信息很难以精确数来表示，而直觉梯形模糊数同时考虑了隶属度、非隶属度和犹豫度等三方面的信息，能更为细腻地刻画客观世界的不确定性，在处理不确定信息时极为有效。此外，注意到评估指标之间往往无法满足独立性假设，而是存在或互补或冗余等关联关系，而文献[13，14]所提出的基于Choquet积分和扩展Shapley值的信息集结算子，能更加全面反映不同指标间的相互关系，并可处理非独立情形下的信息集结过程。综上所述，本文对铁路应急预案的评估体系展开研究，并以此为基础提炼出应急预案的评估指标体系；考虑多方意见的重要性以及信息评估方式的合理性，邀请多位专家利用直觉梯形模糊数表征应急预案各项指标的评估值；考虑前景理论在刻画专家心理偏好方面的有效性，获取相应于各专家的各预案评估指标的综合前景值；考虑各评估指标间的关联关系，基于Choquet积分和扩展Shapley值对各指标的综合前景值进行集结，并利用投影法求解各专家的权重。由此，可集结各专家的意见以确定各应急预案的综合前景值，并以此对其排序，获取最优应急预案。

1 铁路应急预案评估指标体系的构建

1.1 评估指标的选取

铁路应急预案是指铁路各级职能部门为有效预防和控制各类突发事件，在辨识与评估潜在危险源、事件类型、发生的可能性及发生过程、后果及影响严重程度的基础上，而预先制定的一套切实、迅速、有效、有序的处置方案与行动计划[15]，它不仅规定了组织指挥机构与职责、应急法律法规、应急保障措施、宣传、培训、演练及风险源监控等常态工作，也明确了预警行动、分级相应、应急指挥与协调、应急处置、应急避险、应急结束、后期处置等非常态工作。因此，铁路应急预案质量的优劣直接影响到应急救援的效果和效率。指标体系是一套能够全面反映铁路应急预案特征，并具有内在联系，起互补作用的指标集合。科学建立铁路应急预案指标体系，是对铁路应急预案进行评估成功与否的关键。本文在现有研究的基础上，根据铁路突发事件及应急管理的特点，提出从应急预案的处置时效性、可操作性、完备性、责任明确性、经济性等5个方面对铁路应急预案进行评估。表1给出了本文所建立的铁路应急预案评估指标参考标准。

表1 铁路应急预案评估指标参考标准

由表1可知，每一个评估指标均规定了若干项具体的要求，如时效性规定了7项、可操作性9项、完备性13项、责任明确性7项以及经济性6项。评估专家对候选预案的指标进行评估，即是对该指标所包含的各项要求完成的总体情况进行评估。因此，专家在给出指标的评估值之前，必须先评估该指标所对应的各项具体要求，再综合每项要求的得分情况确定该指标的评估值。考虑到直觉梯形模糊数表述不确定信息的优点，本方法组织评估专家采用直觉梯形模糊数对各项要求及指标打分，为规范专家打分，防止打分过程中产生过大偏差，本文给出了打分标准，见表2。实际上，本文所提出的方法为一类静态评估方法，出于节省时间与经济成本的考量，本方法要求专家在综合考虑指标所包含各项要求的基础上给出预案各指标的最终得分，作为进一步评估的依据。

表2 评估专家打分标准

1.2 直觉梯形模糊数

为便于后续描述，本节简要介绍直觉梯形模糊数的相关理论基础。

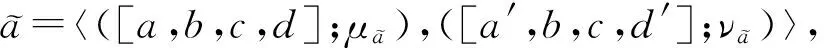
( 1 )

非隶属函数为

( 2 )

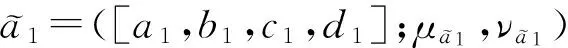
( 3 )

2 铁路应急预案决策模型

为后续表述便利，下面的符号用以描述铁路应急预案评估问题中所涉及的相关集合与变量。

T={t1，t2，…，tl}：l位对铁路应急预案予以评估的专家，其中tk表示第k个专家，k=1，2，…，l。

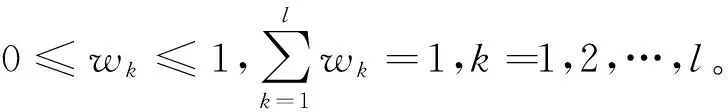
R={r1，r2，…，rm}：m个备选铁路应急预案集合，其中ri表示第i个铁路应急预案，i=1，2，…，m。

Z={z1，z2，…，zn}：n个铁路应急预案评估指标的集合，其中zj表示第j个指标，本文选取时效性、可操作性、完备性、责任明确性以及经济性等5个指标对预案评估，j=1，2，…，n，本文取n=5。

S={S1，S2，…，Sh}：若选择某个铁路应急预案应对相应的突发事件，在应急过程中各评估指标可能出现的情景的集合，其中Sg表示第g个可能的情景，g=1，2，…，h。

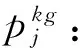
铁路应急预案的评估问题作为风险决策问题，可采用图1的形式予以描述。

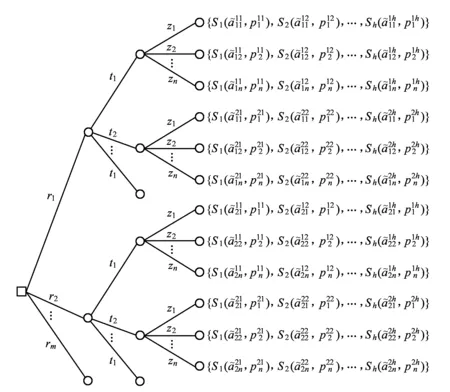
图1 铁路应急预案风险评估问题

2.1 指标综合前景值的计算

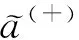
( 4 )

( 5 )

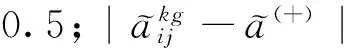
( 6 )

( 7 )

式中：k=1，2…l；i=1，2，…，m。

( 8 )

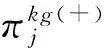
( 9 )

(10)

式中：参数χ和δ表示专家在面临“收益”和“损失”情形下主观概率函数的弯曲程度；k=1，2，…，l；j=1，2，…，n；g=1，2，…，h。

关于参数α、β、θ、χ和δ的取值问题，文献[9]通过对大量的决策个体进行实验测试，给出了与实验结果最为一致的取值为α=β=0.88、θ=2.25、χ=0.61和δ=0.69。学者普遍认为上述取值有效地表示任意决策者的大致心理行为偏好[17，18]，故本文在此采用该参数取值。

(11)

式中：k=1，2，…，l；i=1，2，…，m；j=1，2，…，n。

2.2 集结相应于各指标的评估值

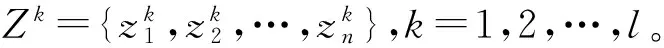
针对专家tk，指标集合Zk的幂集为P(Zk)，即指标集合Zk的所有子集的集合。这里令μ为定义在P(Zk)上的集函数μ：P(Zk)→[0，1]，如果μ满足以下条件，则称μ为模糊测度：①μ(Ø)=0，μ(Zk)=1；②如果A，B∈P(Zk)，A⊆B，则μ(A)≤μ(B)。如果模糊测度μ满足μ(A∪B)=μ(A)+μ(B)+λμ(A)μ(B)，则称μ为λ模糊测度，其中λ∈(-1，∞)。

对于各指标集A⊆Zk，λ模糊测度μ(A)可通过式(12)求得[13]。

(12)

由于μ(Zk)=1，参数λ可由式(13)确定[13]。

(13)

针对专家tk，已知集合Zk的幂集P(Zk)及定义在P(Zk)上的模糊测度μ，对于∀A∈P(Zk)，其扩展Shapley值[14]为

(μ(A∪B)-μ(B))

(14)

(15)

(16)

2.3 集结相应于各专家的评估值

3 算例

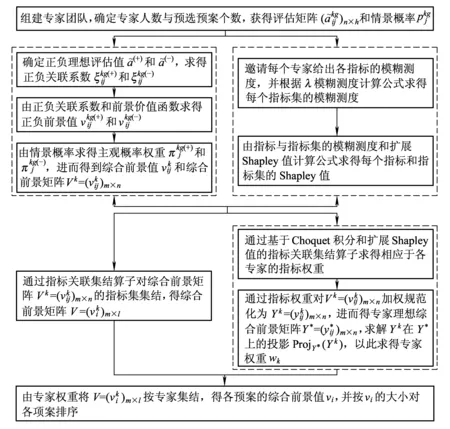
图2 铁路应急预案评估流程

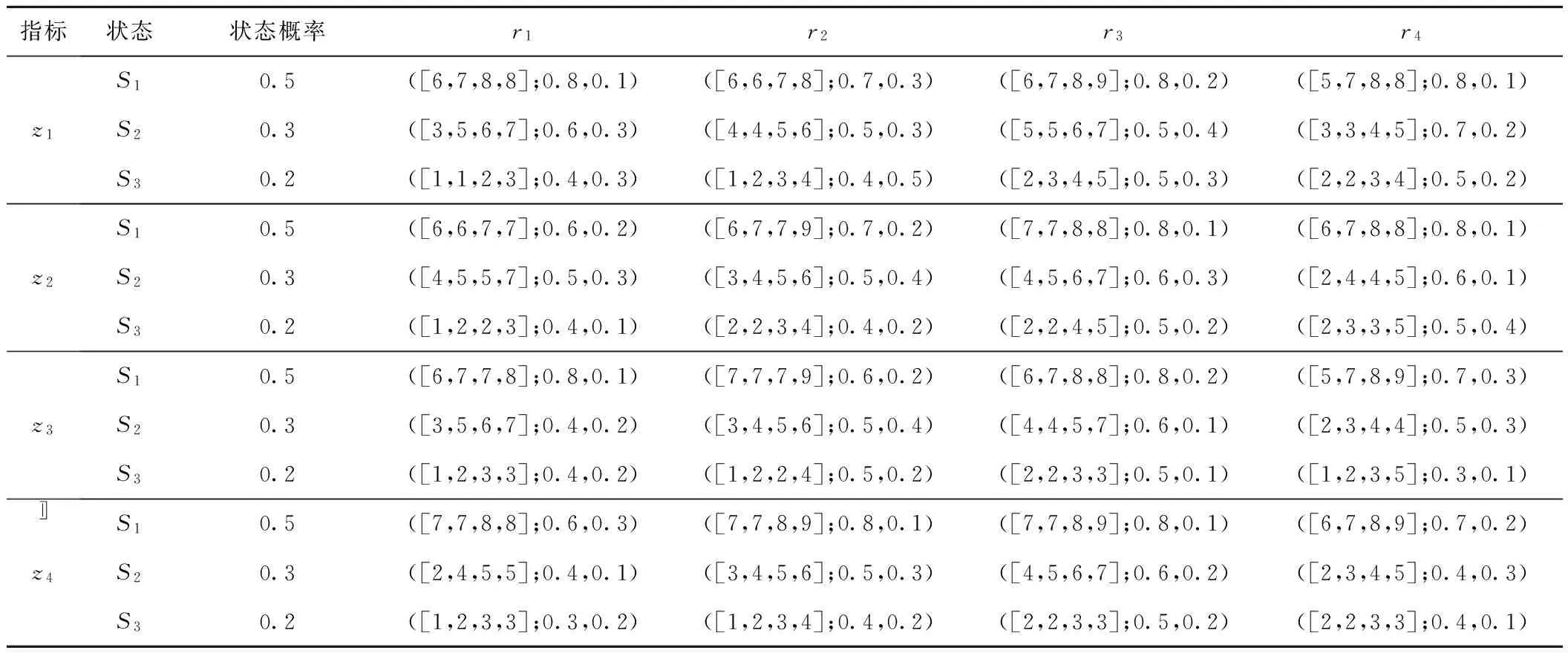
指标状态状态概率r1r2r3r4z1S10.5([6,7,8,8];0.8,0.1)([6,6,7,8];0.7,0.3)([6,7,8,9];0.8,0.2)([5,7,8,8];0.8,0.1)S20.3([3,5,6,7];0.6,0.3)([4,4,5,6];0.5,0.3)([5,5,6,7];0.5,0.4)([3,3,4,5];0.7,0.2)S30.2([1,1,2,3];0.4,0.3)([1,2,3,4];0.4,0.5)([2,3,4,5];0.5,0.3)([2,2,3,4];0.5,0.2)z2S10.5([6,6,7,7];0.6,0.2)([6,7,7,9];0.7,0.2)([7,7,8,8];0.8,0.1)([6,7,8,8];0.8,0.1)S20.3([4,5,5,7];0.5,0.3)([3,4,5,6];0.5,0.4)([4,5,6,7];0.6,0.3)([2,4,4,5];0.6,0.1)S30.2([1,2,2,3];0.4,0.1)([2,2,3,4];0.4,0.2)([2,2,4,5];0.5,0.2)([2,3,3,5];0.5,0.4)z3S10.5([6,7,7,8];0.8,0.1)([7,7,7,9];0.6,0.2)([6,7,8,8];0.8,0.2)([5,7,8,9];0.7,0.3)S20.3([3,5,6,7];0.4,0.2)([3,4,5,6];0.5,0.4)([4,4,5,7];0.6,0.1)([2,3,4,4];0.5,0.3)S30.2([1,2,3,3];0.4,0.2)([1,2,2,4];0.5,0.2)([2,2,3,3];0.5,0.1)([1,2,3,5];0.3,0.1)z4S10.5([7,7,8,8];0.6,0.3)([7,7,8,9];0.8,0.1)([7,7,8,9];0.8,0.1)([6,7,8,9];0.7,0.2)S20.3([2,4,5,5];0.4,0.1)([3,4,5,6];0.5,0.3)([4,5,6,7];0.6,0.2)([2,3,4,5];0.4,0.3)S30.2([1,2,3,3];0.3,0.2)([1,2,3,4];0.4,0.2)([2,2,3,3];0.5,0.2)([2,2,3,3];0.4,0.1)〛

续上表

表4 专家t2所提供的评估值

表5 专家t3所提供的评估值

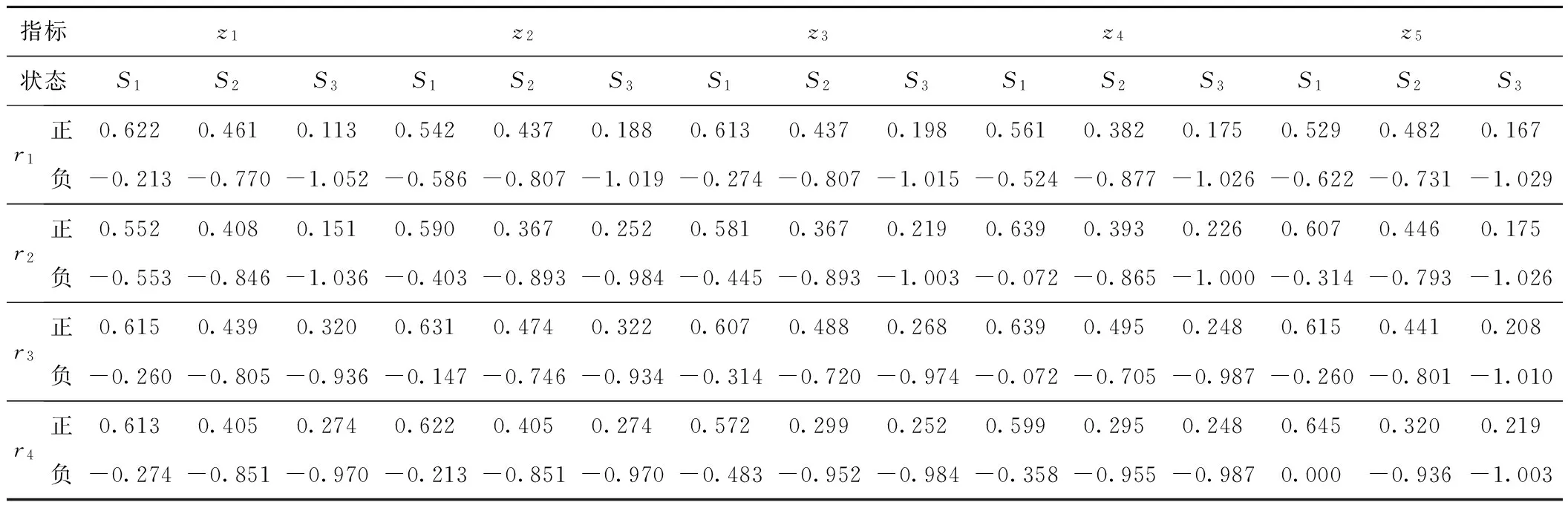
表6 相应于专家t1各评估值的正、负前景值

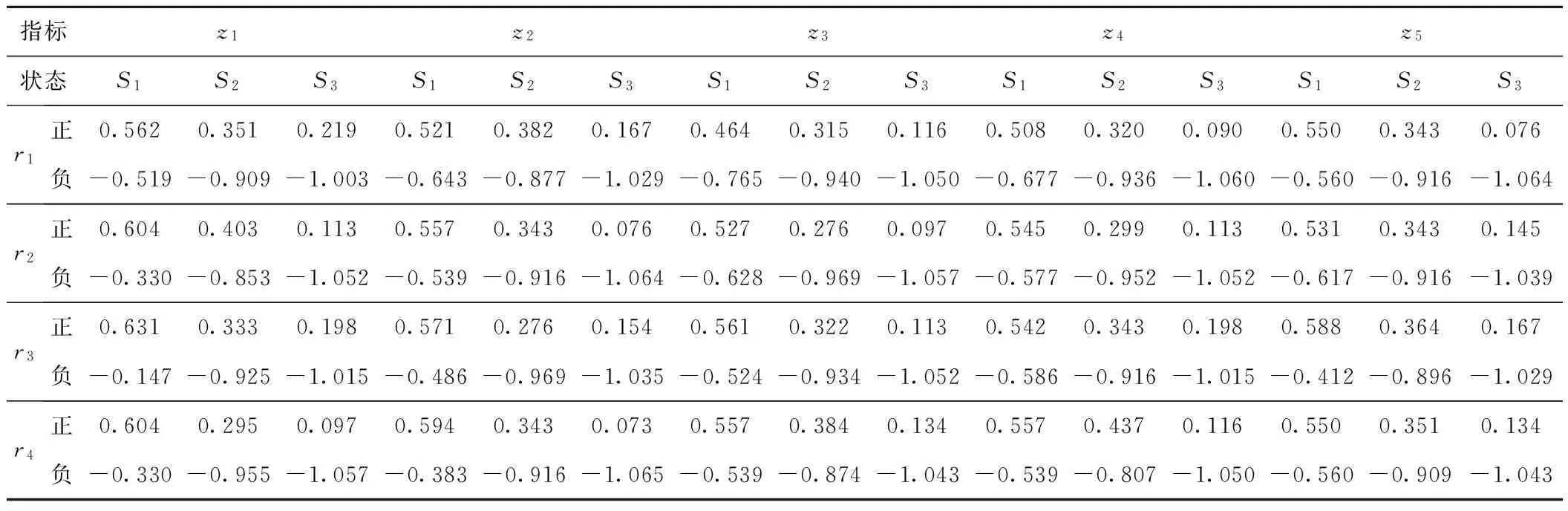
表7 相应于专家t2各评估值的正、负前景值

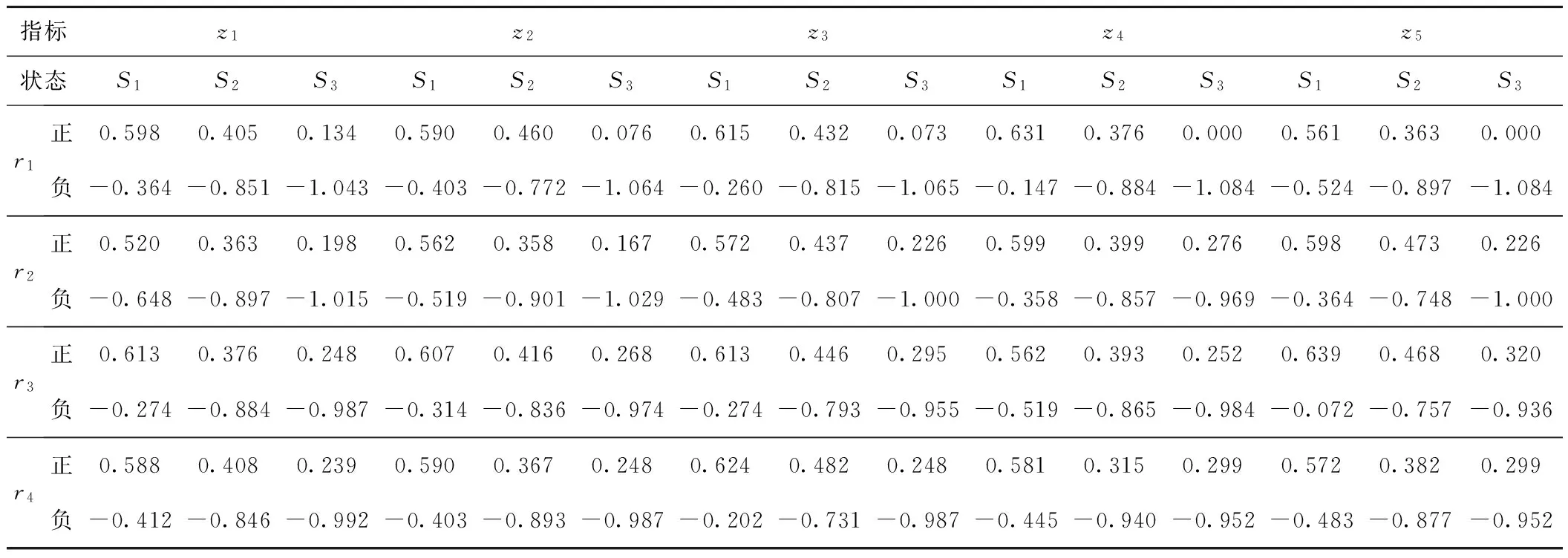
表8 相应于专家t3各评估值的正、负前景值

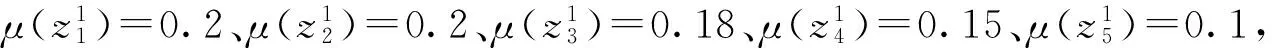
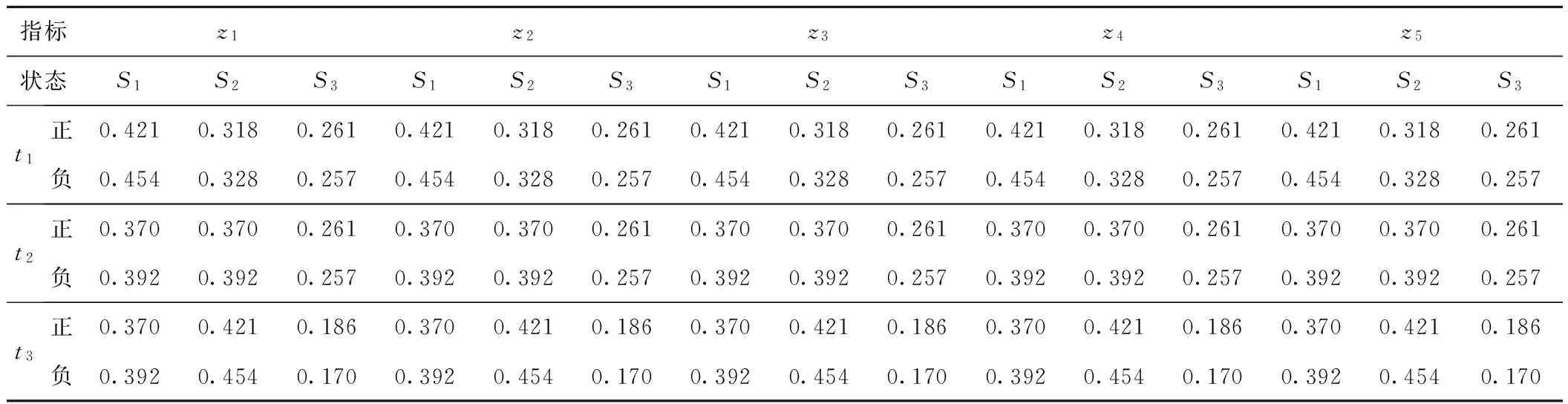
表9 专家面临“收益”和“损失”时的前景权重函数

表10 相应于专家tk的各应急预案ri下指标zj评估值的综合前景值

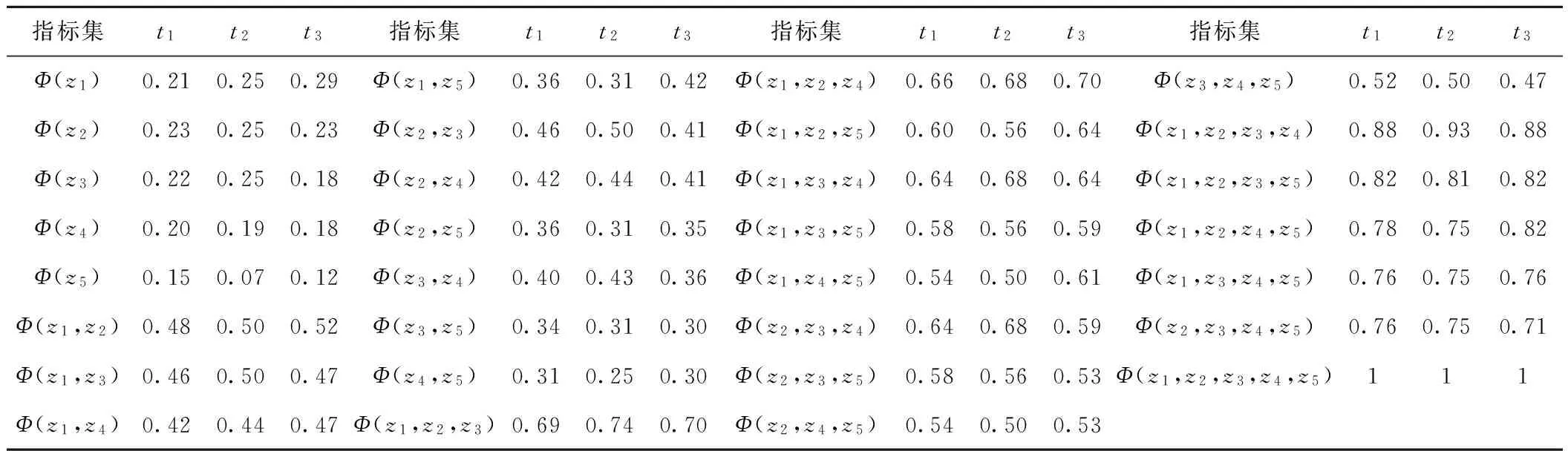
表11 相应于专家t1、t2和t3的指标及指标集的扩展Shapley值

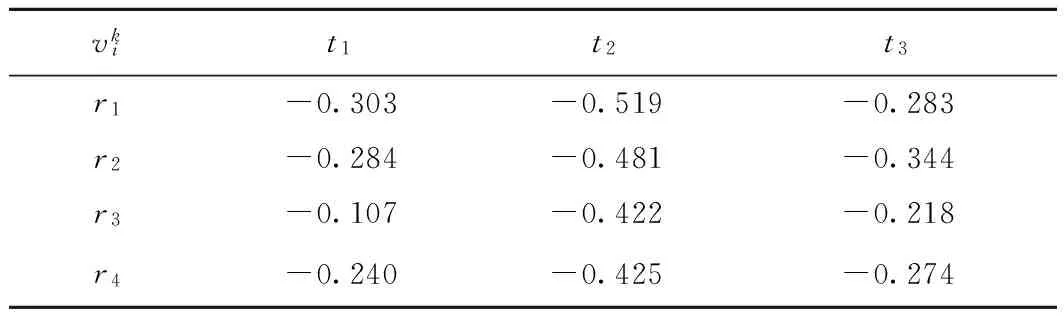
表12 相应于各专家的各项应急预案的综合前景矩阵

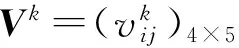
表13 综合前景矩阵的加权规范化

表14 相应于各专家的理想综合前景矩阵

该案例中的4个候选应急预案是在预案编写小组充分考虑各种因素的情况下编制的，而后以时效性、可操作性、完备性、责任明确性、经济性作为评估指标，通过上述步骤，专家选出了最优预案，即预案r3。针对所选择的最优预案可能存在某些细节未能考虑到或考虑得并不充分的情况，本文给出基于上述评估方法的周期性评估过程：针对所选出的最优预案，邀请铁路相关部门配合实施或演练该预案，也可模拟该过程，通过分析找出未能考虑到或考虑得并不充分的细节，并形成一定的反馈信息；将该反馈信息引入到本文所提的评估方法中，如若某些关键的细节在该评估方法中并未考虑，可将关键细节引入到指标体系中，作为对预案集下次评估的指标；基于新的指标体系，再次采用本文所提的评估方法，从预案集中选出最优预案。通过多次演练与评估，直至未能发现新的关键细节，即可在尽可能考虑各种细节的情况下选出最优预案，也可由此找出最优预案中的薄弱环节。

4 结束语

针对铁路突发事件，选择完善、有效的应急预案，有助于迅速、高效处置突发事件并尽可能将由此造成的损失降到最低，具有重要的现实意义。为科学合理地从众多候选预案集中确定最优铁路应急预案，本文提出了基于前景理论的铁路应急预案多指标风险评估方法。通过对铁路应急预案的评估体系展开分析研究，提出从时效性、可操作性、完备性、责任明确性和经济性等5个方面对应急预案进行评估。同时，利用基于直觉梯形模糊数和前景理论的多指标风险决策方法评估铁路应急预案，不仅有效地刻画了信息的不确定性，也充分考虑了专家的主观偏好。本文方法还引入了基于Choquet积分和扩展Shapley值的集结算子，并采用投影法求解专家权重，可更为准确地描述各评估指标间的关联关系。通过对某铁路局制定的应对列车脱轨事件的铁路应急预案进行评估，阐释了本文方法的可行性与有效性。

参考文献：

[1]程晓卿,贾利民,秦勇,等.铁路应急管理研究[J].铁道学报,2012,34(3):7-13.

CHENG Xiaoqing,JIA Limin,QIN Yong,et al.Research on Railway Emergency Management[J].Journal of the China Railway Society,2012,34(3):7-13.

[2]罗文婷,王艳辉,贾利民,等.改进层次分析法在铁路应急预案评价中的应用研究[J].铁道学报,2008,30(6):24-28.

LUO Wenting,WANG Yanhui,JIA Limin,et al.Application of Improved AHP in Evaluation of Railway Emergency Plans[J].Journal of the China Railway Society,2008,30(6):24-28.

[3]唐士晟,李小平.铁路交通事故应急救援体系脆弱性评价方法研究[J].铁道学报,2013,35(7):14-20.

TANG Shisheng,LI Xiaoping.Study on method for Assessment of Vulnerability of Railway Emergency Rescue System[J].Journal of the China Railway Society,2013,35(7):14-20.

[4]祝凌曦,肖雪梅,李玮,等.基于改进DEA法的铁路应急预案编制绩效评价方法研究[J].铁道学报,2011,33(4):1-6.

ZHU Lingxi,XIAO Xuemei,LI Wei,et al.Research on Performance Evaluation of Compilation of Railway Emergency Plan Based on Improved DEA Method[J].Journal of the China Railway Society,2011,33(4):1-6.

[5]张振海,王晓明,党建武,等.基于整体相似度的铁路应急救援预案推理决策方法研究[J].铁道学报,2012,34(11):49-53.

ZHANG Zhenhai,WANG Xiaoming,DANG Jianwu,et al.Research on CBR Decision Method of Railway Emergency Rescue Based on Integral Similarity Degree[J].Journal of the China Railway Society,2012,34(11):49-53.

[6]JU Y B,WANG A H.Emergency Alternative Evaluation under Group Decision Makers:A Method of Encorporating DS/AHP with Extended TOPSIS[J].Expert Systems with Applications,2012,39(1):1 315-1 323.

[7]樊治平,刘洋,沈荣鉴.基于前景理论的突发事件应急响应的风险决策方法[J].系统工程理论与实践,2012,32(5):977-984.

FAN Zhiping,LIU Yang,SHEN Rongjian.Risk Decision Analysis Method for Emergency Response Based on Prospect Theory[J].Systems Engineering-Theory & Practice,2012,32(5):977-984.

[8]KAHNEMAN D,TVERSKY A.Prospect Theory:An Analysis of Decision under Risk[J].Econometrica,1979,47(2):263-291.

[9]TVERSKY A,KAHNEMAN D.Advances in Prospect Theory:Cumulative Representation of Uncertainty[J].Journal of Risk and Uncertainty,1992,5(4):297-323.

[10]KROHLING R A,DE SOUZA T T M.Combining Prospect Theory and Fuzzy Numbers to Multi-criteria Decision Making[J].Expert Systems with Applications,2012,39:11 487-11 493.

[11]LIU Y,FAN Z P,ZHANG Y.Risk Decision Analysis in Emergency Response:A Method Based on Cumulative Prospect Theory[J].Computers & Operations Research,2014,42:75-82.

[12]陈振颂,李延来.基于前景ITFNCI算子的群体MULTIMOORA决策方法[J].控制与决策,2014,29(6):1 053-1 063.

CHEN Zhensong,LI Yanlai.An Approach for Group Multi-attribute Decision Making Based upon Prospect Intuitionistic Trapezoidal Fuzzy Number Choquet Integral Operator[J].Control and Decision,2014,29(6):1 053-1 063.

[13]MENG F Y,ZHANG Q,CHENG H.Approaches to Multiple-criteria Group Decision Making Based on Interval-valued Intuitionistic Fuzzy Choquet Integral with Respect to the Generalized λ-Shapley Index[J].Knowledge-Based Systems,2013,37:237-249.

[14]MENG F Y,TAN C Q,ZHANG Q.The Induced Generalized Interval-valued Intuitionistic Fuzzy Hybrid Shapley Averaging Operator and Its Application in Decision Making[J].Knowledge-Based Systems,2013,42:9-19.

[15]周慧娟.铁路应急管理中的预案管理与资源配置优化[D].北京:北京交通大学,2011:51-52.

[16]王坚强,张忠.基于直觉梯形模糊数的信息不完全确定的多准则决策方法[J].控制与决策,2009,24(2):226-230.

WANG Jianqiang,ZHANG Zhong.Multi-criteria Decision-making Method with Incomplete Certain Information Based on Intuitionistic Fuzzy Number[J].Control and Decision,2009,24(2):226-230.

[17]BIRNBAUM M H.Three New Tests of Independence That Differentiate Models of Risky Decision Making[J].Management Science,2005,51(9):1 346-1 358.

[18]HE X D,ZHOU X Y.Portfolio Choice under Cumulative Prospect Theory:An Analytical Treatment[J].Management Science,2011,57(2):315-331.

[19]YUE Z.Application of the Projection Method to Determine Weights of Decision Makers for Group Decision Making[J].Scientia Iranica,2012,19(3):872-878.