基于概率需求的高速铁路无砟轨道板温度荷载取值研究Ⅰ：轴向均匀温度作用

欧祖敏，孙 璐，2，周 杰，赵国堂

(1.东南大学 交通学院，江苏 南京 210096；2.美国华盛顿Catholic大学 土木工程系，华盛顿 20064；3.中国铁路总公司，北京 100844)

无砟轨道结构因整体性好、变形小、维修工作量少等优点被广泛应用于高速铁路[1]。但曝露于大气环境下的混凝土无砟轨道板易受环境温度作用影响产生不均匀变形，轨道板变形受到约束后将产生温度应力[2]。在设计控制轨道板温度应力时，需要确定其可能承受的温度荷载，文献[3] 认为无砟轨道中的年温度变化与气温变化幅度相等，最大年温差可以按所在年内月份最高与最低平均温度的差值计算，但这难以真实反映轨道板年最大温差的实际特征。我国现行高速铁路设计规范推荐无砟轨道结构的年温差根据当地气象条件取值，混凝土收缩取等效温降10 ℃，常用温度梯度取45 ℃/m，但未指出年温差如何取值、取多大的值，常用温度梯度取45 ℃/m也有些笼统[4]。以往的荷载规范很少对温度荷载做出明确规定或仅参考了行业及国外标准来考虑温度作用的计算方法，各类参数取值不规范、不统一，文献[5]虽然初次纳入了温度作用，但也仅初步给出温度作用的定义、表达和标准值取值说明，离实际应用仍有差距[6]。因此，有必要对轨道板温度荷载的取值进行研究。

本文根据文献[5，7]中关于可变作用的有关规定及取值要求，结合高速铁路无砟轨道板经历温度荷载的实际情况，对无砟轨道板的温度荷载取值进行研究，为无砟轨道结构设计中关于温度荷载的确定提供简便、合理的方法。因轨道板温度荷载主要包括轴向均匀温度荷载和温度梯度荷载两种类型，本研究将分两篇文章对轴向均匀温度荷载和温度梯度进行取值。

1 无砟轨道板温度荷载

1.1 无砟轨道板温度场方程

文献[8]研究表明，无砟轨道结构内的温度分布与其表面温度的变化密切相关。对均质的混凝土无砟轨道板，研究中为计算轨道结构的温度场，建立轨道结构温度场与外界环境(气象条件)的关系，并通过现场实测对轨道结构温度场方程进行初步验证，利用轨道板所在地区城市气象资料可计算得到轨道板历年的温度分布数据，轨道板每日的温度场可表示为[9]

( 1 )

1.2 无砟轨道板轴向均匀温度作用

文献[10]把混凝土梁板中非线性的温度分布分解为轴向均匀温度、线性温差(温度梯度)和非线性温差三部分，其中非线性温差部分仅对混凝土梁板产生自平衡应力，不对结构整体产生荷载效应。文献[5]规定对混凝土普通尺寸梁板结构的温度荷载作用主要考虑轴向均匀温度变化与线性温度梯度变化的作用效应。由式( 1 )可以看出，轨道板每日承受的温度荷载具有周期性，轨道板的温度荷载日最大值和日最小值能反映其特征，因此，轨道承受的温度荷载可主要考虑轴向均匀温度日最大值、最小值和正、负温度梯度日最大值、最小值。轨道板的轴向均匀温度即为温度沿其高度的平均值，对式( 1 )积分可得轨道板轴向均匀温度日最值表达式分别为

(h=0.2)

( 2 )

(h=0.2)

( 3 )

从式( 2 )和式( 3 )可以看出，轨道板轴向均匀温度荷载的大小与板厚有关，轨道板轴向均匀温度日最大值、最小值与板厚的关系如图1所示。从图1可以看出，轴向均匀温度日最大值随板厚的增加而减小，最小值随板厚的增加而增大，但对厚度在0.2～0.3 m之间的普通轨道板，其轴向均匀温度的变化趋势一致，数值最大差异2～3 ℃，为减少计算量本文以0.2 m厚轨道板为对象进行分析。

(a)7月

(b)10月图1 北京地区2011年夏、秋季轨道板轴向均匀温度日最大值与气温日最大值变化趋势

2 无砟轨道板温度荷载极值概率模型

影响轨道板温度场及温度荷载的环境因素随时间变化，这使温度荷载也具有时间随机性。大量研究指出[11-13]：对具有随机特性的工程荷载，采用随机过程模型来描述较为切合实际。在描述轨道板温度荷载时，假定任意时点荷载为Q(t)，将轨道板的几种温度荷载模型转化为随机过程{Q(t)，t∈[0，T]}，根据荷载随时间变化的样本函数或已有荷载分布的特征，确定设计基准期内荷载最大值QT。目前主要有平稳二项随机过程模型和极值概率模型两种方法，其中极值概率模型适用性最广，参考其原理并给出温度荷载极值概率模型的步骤如下[13，14]：

(1)无砟轨道结构的设计基准期为T年(暂定T=60)。

(3)通过调查统计获得时段τi内荷载最大值Qi，max(随机变量)的分布Fτi，max(x)，并假定各时段的Qi，max相互独立且具有相同的分布函数Fτi，max(x)，根据最大值的极值分布原理可得设计基准期内最大温度荷载为：QT，max=max{Q1，max，Q2，max， …，QN，max}，相应的设计基准期内最大温度荷载QT，max的分布为[15，16]

FT(QT，max)=P(QT，max≤x)

=P(Q1，max≤x，Q2，max≤x，…，QN，max≤x)

=P(Q1，max≤x)·P(Q2，max≤x)·…·

P(QN，max≤x)=[Fτi，max(x)]N

( 4 )

如需要的荷载为设计基准期内的最小值(最低温度荷载)，则先调查统计各时段内的最小值Qi，min(随机变量)的分布Fτi，min(x)，同样假定各时段的Qi，min相互独立且具有相同的分布函数Fτi，min(x)，根据最小值的极值分布原理可得设计基准期内最小荷载为：QT，min=min{Q1，min，Q2，min，…，QN，min}，相应的设计基准期内最小荷载QT，min的分布为[15，16]

FT(QT，min)=P(QT，min≤x)=1-P(QT，min>x)

=1-P(Q1，min>x，Q2，min>x，…，QN，min>x)

=1-P(Q1，min>x)·P(Q2，min>x)·…·

P(QN，min>x)=1-[1-Fτi，min(x)]N

( 5 )

(4)由时段概率分布Fτi(x)及其统计参数根据上式给出相当于T年N个时段最大(小)荷载QT，max(min)的分布FT，max(min)(x)及统计参数。

3 无砟轨道板轴向均匀温度作用统计分析与概率分布

利用历史气象资料(在中国气象科学数据共享服务网可查询不同台站的气象资料，其格式、内容及完整性见具体数据库)可以计算我国不同地区无砟轨道板的多年温度荷载历程，作为城市所在地轨道板温度荷载分布规律的数据样本。

3.1北京地区气温与轴向均匀温度日最值频数直方图

将同一地区轨道板多年的轴向均匀温度荷载日最值(轴向均匀温度日最大值、轴向均匀温度日最小值)数据进行处理，可以得到所在城市标准轨道板(厚度0.2 m)轴向均匀温度日最值每年的频数直方图，为与当地气温进行比较，同时给出了所在城市气温日最值每年的频数直方图，如图2所示。

(a)气温日最大值(b)气温日最小值(c)轨道板轴向均匀温度日最大值(d)轨道板轴向均匀温度日最小值

图2 北京地区1958～2011年历年气温日最值、轴向均匀温度日最值统计直方图

从图2可以看出，北京地区轨道板多年的轴向均匀温度日最值与当地多年的气温日最值分布规律相似，但轴向均匀温度日最值和气温日最值分布规律都有些复杂，难以看出其分布函数，为此，对各地的轨道板历年轴向均匀温度日最值数据再次进行加工处理。以不同年份的月份为统计时段进行分析，得到轨道板轴向均匀温度日最值不同月份的频数直方图如图3、图4所示。

(a)气温日最大值(b)气温日最小值(c)轨道板轴向均匀温度日最大值(d)轨道板轴向均匀温度日最小值

图3 北京地区1962～2011年历年1月气温日最值、轴向均匀温度日最值统计直方图

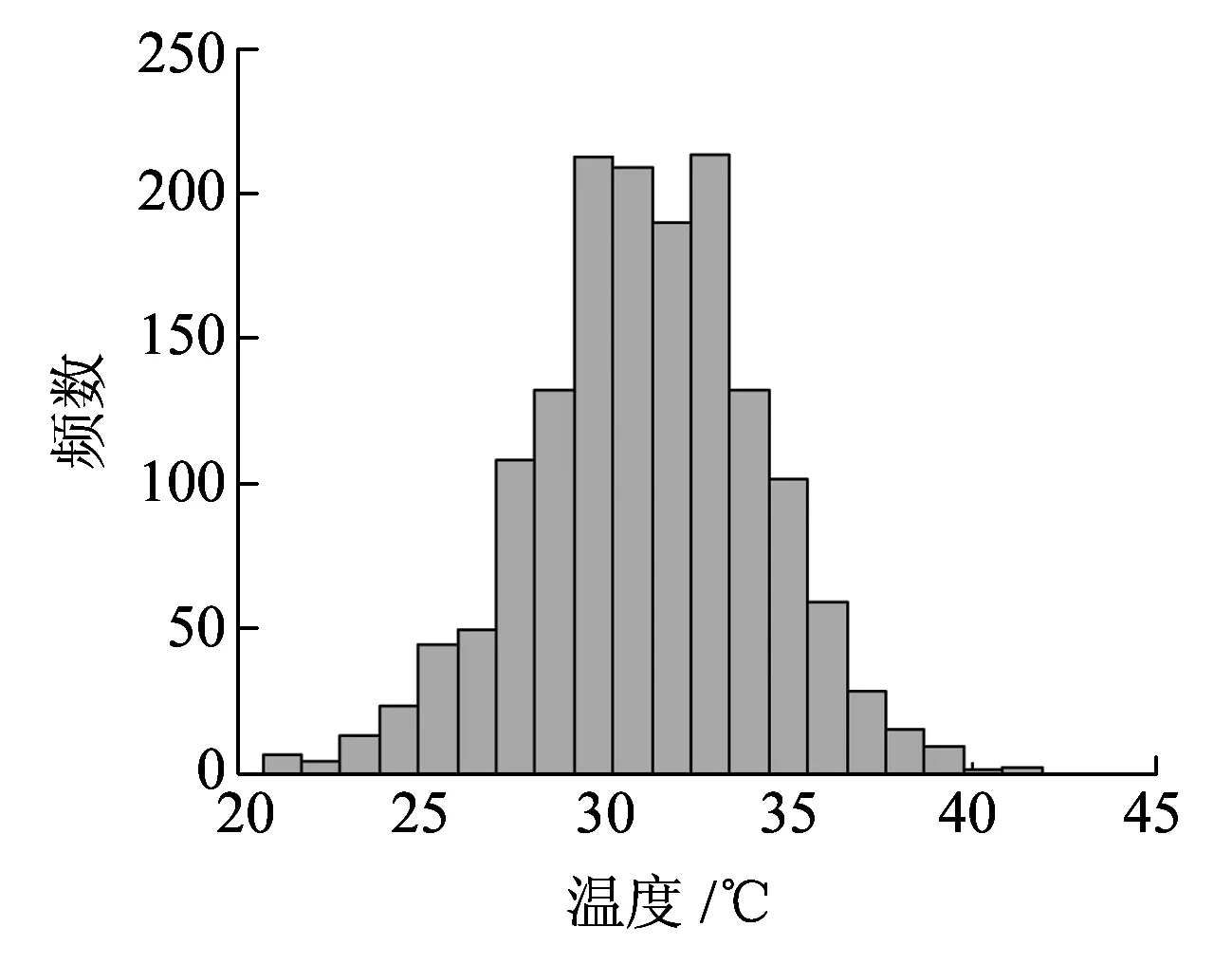
(a)气温日最大值

(b)气温日最小值图4 北京地区1962～2011年历年7月气温日最值统计直方图

3.2北京地区气温与轴向均匀温度日最值分布拟合及检验

图3、图4表明，月份的气温日最值、轨道板轴向均匀温度日最值均有呈正态分布的趋势，可以利用正态分布函数来拟合其分布规律。设连续型随机变量x的概率密度函数为

( 6 )

式中：μ、σ(σ>0)是常数，称x服从参数为μ、σ2的正态分布或高斯分布，记为X～N(μ，σ2)。

利用正态分布函数对不同月份的气温日最值、轨道板轴向均匀温度日最值进行拟合，通过matlab软件中参数估计及Jarque-Bera检验(K-S检验的一种)功能，取显著性水平α=5%进行正态分布拟合优度检验，与图3、图4北京地区历年部分月份的温度日最值频数直方图相对应的正态分布概率图如图5、图6所示，不同月份的温度日最值正态分布参数估计值见表1。虽然少数月份温度日最值的正态分布拟合优度检验没有通过，但其温度日最值的统计直方图仍呈明显的单峰形态，整体趋近于正态分布，本文仍将这部分月份温度日最值分布近似为正态分布。

(a)气温日最大值

(b)气温日最小值

(c)轨道板轴向均匀温度日最大值

(d)轨道板轴向均匀温度日最小值图5 北京地区1962～2011年历年1月气温日最值、轴向均匀温度日最值正态分布概率图

(a)气温日最大值

(b)气温日最小值图6 北京地区1962～2011年历年7月气温日最值正态分布概率图

3.3哈尔滨地区气温与轴向均匀温度日最值分布参数估计值

按前述方法对哈尔滨地区气温、轨道板轴向均匀温度日最值每月的分布函数进行统计分析，得到正态分布的参数估计值见表2。分布检验结果表明大部分月份的温度日最值都不拒绝正态分布，少部分月份没有通过检验。这些没有通过检验月份的温度基本处于温度数值范围的中间位置，对温度取值的端部分布影响有限，考虑其频数直方图趋于正态分布，为简化计算仍采用正态分布拟合所在月份的温度日最值分布。

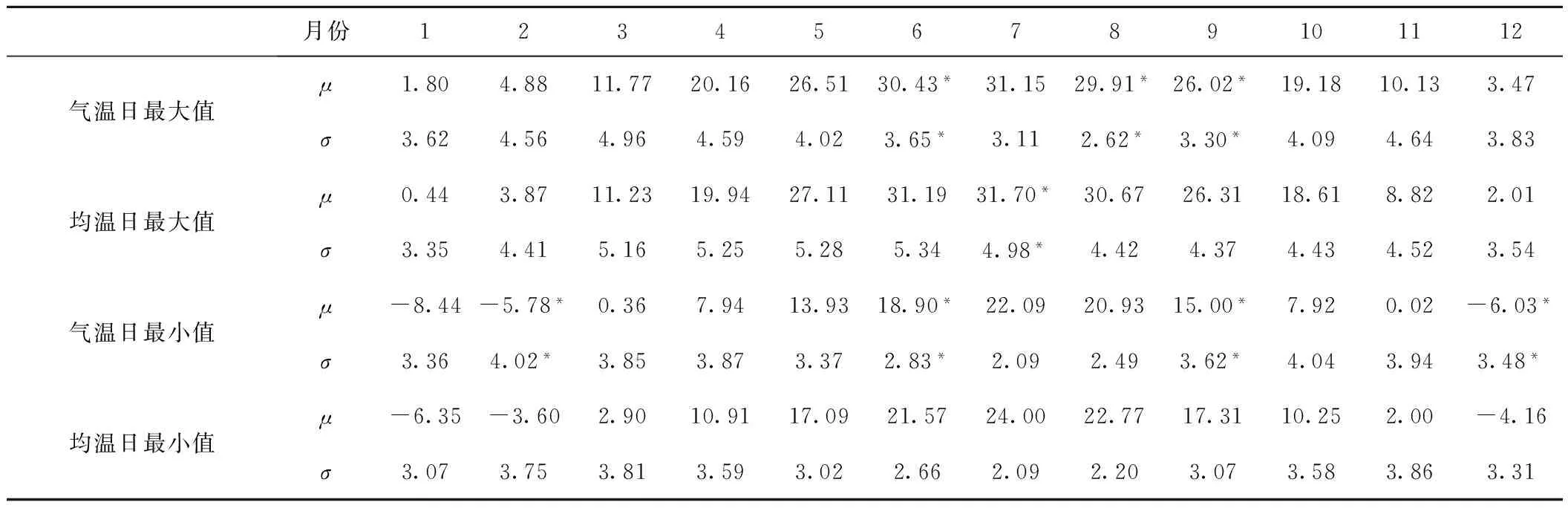
表1 北京地区1962～2011年不同月份气温日最值、轨道板轴向均匀温度日最值正态估计参数

*为正态分布拟合优度Jarque-Bera检验未通过的月份。

表2 哈尔滨地区1962～2011年不同月份气温日最值、轨道板轴向均匀温度日最值正态估计参数

*为正态分布拟合优度Jarque-Bera检验未通过的月份。

3.4 气温与轴向均匀温度日最值年分布函数

利用前述历年不同月份气温与轴向均匀温度日最值样本统计分析获得的时段温度分布函数参数估计值，即可求得所在地区(i表示月份编号，i=1，2，…，12)气温与轴向均匀温度不同月份的概率分布函数。

( 7 )

式中：Fτ -m，i(x)为一年中第i月的气温与轴向均匀温度日最值的概率分布函数；μi、σi分别为第i月气温与轴向均匀温度日最值分布函数参数估计值。

每年由12个月组成，月份分布之间相互独立，根据互不相容事件的可加可列性特征，可知一年的分布概率由每个月的分布概率按一定比例(当月天数与当年天数比值)之和构成，利用月份温度日最值概率分布函数可得到相应温度日极值的年概率分布函数为

Fτ -y(x)=ω1Fτ -m，1(x)+ω2Fτ -m，2(x)+…+

ω12Fτ -m，12(x)

( 8 )

式中：Fτ -y(x)为温度日最值的年概率分布函数；ωi为第i个月的月份分布概率在年分布概率中的比例(权重)，其数值为当月天数与当年天数比值，也可近似取ωi=1/12。

根据荷载概率模型式( 4 )和式( 5 )，可以得到设计基准期T内荷载最大值QT，max、最小值QT，min(最低温度荷载)的分布FT，max(x)、FT，min(x)为

( 9 )

式中：FT，max(x)、FT，min(x)分别为设计基准期T内温度荷载日最大值、最小值分布函数。

4 无砟轨道板轴向均匀温度作用分位值(标准值)的确定

荷载标准值由设计基准期内最大荷载(或最小荷载)概率分布统计特征值或某个分位值确定，文献[7，17]均规定按此方法确定可变作用标准值，但都没有对设计基准期长度和取值分位值做统一规定。

我国房屋建筑结构的设计基准期为50年，而铁路、公路桥涵结构的设计基准期为100年，为此，本文分别对设计基准期为T=50年和T=100年，分位概率P=50%、90%、95%(相应的设计基准期荷载最大值超越概率1-P分别为50%、10%、5%，荷载最小值超越概率为P)的各分位值进行计算，确定相应温度荷载标准值QT。另外，考虑到温度荷载为自然作用，采用重现期TR(年)(重现期是指连续两次超过作用值Qk)来表达可变作用的标准值QTR比较方便，取重现期为TR=50年、60年、100年，相应的年保证率1-1/TR分别为98%、98.3%和99%(对应的荷载最大值年超越概率1/TR为2%、1.7%和1%，荷载最小值年超越概率为(1-1/TR))。分别代入式( 9 )和式( 8 )，可得温度荷载分位值(标准值)的表达式为

(10)

利用分布拟合得到的温度分布函数参数估计值，根据式(10)计算可得到各地区常见设计基准期、常见概率(保证概率)的气温、轨道板轴向均匀温度日最值荷载的分位值，见表3、表4；不同设计基准期气温、轨道板轴向均匀温度日最值荷载分位值与保证率(不被超越的概率，也可称为可靠性概率)的关系如图7、图8所示。

表3 北京地区不同概率的气温、轨道板轴向均匀温度日最值荷载分位值 ℃

表4 哈尔滨地区不同概率的气温、轨道板轴向均匀温度日最值荷载分位值 ℃

(a)气温最高值

(b)气温最低值

(c)轨道板轴向均匀温度最大值

(d)轨道板轴向均匀温度最小值图7 北京地区不同设计基准期的气温、轨道板轴向均匀温度日最值保证率概率分布曲线

(a)气温最高值

(b)气温最低值图8 哈尔滨地区不同设计基准期的轨道板轴向均匀温度日最值保证率概率分布曲线

图7、图8为根据各地轨道板轴向均匀温度日最值分布规律，考虑不同设计基准期计算得到的轨道板轴向均匀温度日最值荷载的保证概率曲线，据此可以查询不同设计基准期、不同概率需求(保证概率)的轨道板轴向均匀温度日最值荷载分位值，以满足不同设计需求，应用方便。同时，对其他城市采用相同的方法并结合计算结果，给出表5所示的部分地区气温、轨道板轴向均匀温度日最值荷载标准值(分位概率90%～95%)的推荐值，此推荐值的保证概率在90%～95%之间，与各地区历年的最高、最低气温(保证概率99.7%以上的统计值)相比普遍低3 ℃～5 ℃，既反映了概率水平的差异又证明了本文结果的正确性。

表5 主要地区气温、轨道板轴向均匀温度日最值荷载标准值推荐值 ℃

5 结论

本文根据轨道板所受温度荷载的随机特性建立温度荷载极值概率模型，对标准厚度轨道板轴向均匀温度日极值、所在地区气温日极值的月份分布特征进行分析，计算不同设计基准期、不同概率需求的温度荷载分位值(标准值)，得到如下结论：

(1)利用极值概率模型建立求解轨道板轴向均匀温度日最值、所在地气温日最值的极大、极小值概率模型。

(2)利用城市气象资料和轨道板温度场方程得到标准厚度轨道板的轴向均匀温度日最值，分析轨道板轴向均匀温度和所在地气温日最值的月份分布函数和统计参数，结果表明北京和哈尔滨地区的轴向均匀温度日最值、气温日最值都不拒绝正态概率密度函数；以此为基础得到轨道板轴向均匀温度和所在地气温日最值的年概率分布函数、设计基准期概率分布函数，得到按不同设计基准期和不同重现期定义的轨道板轴向均匀温度日最值荷载最大值、最小值的计算公式。

(3)利用轨道板不同设计基准期和不同重现期的轴向均匀温度日最值荷载最大值、最小值的计算公式，得到常见设计基准期、常见概率的轴向均匀温度日最值荷载的分位值及荷载标准值的推荐值，并给出不同设计基准期轴向均匀温度日最值与保证概率的关系曲线，用于不同概率需求。

参考文献：

[1]SUN L,CHEN L L,ZELELEW H H.Stress and Deflection Parametric Study of High-speed Railway CRTS-Ⅱ Ballastless Track Slab on Elevated Bridge Foundations[J].Journal of Transportation Engineering,2013,139(12):1 224-1 234.

[2]LIU X Y,ZHAO P R,DAI F.Advances in Design Theories of High-speed Railway Ballastless Tracks[J].Journal of Modern Transportation,2011,19(3):154-162.

[3]刘学毅，赵坪锐，杨荣山，等.客运专线无砟轨道设计理论与方法[M].成都：西南交通大学出版社,2010:106-201.

[4]中华人民共和国铁道部.TB 10621—2009 高速铁路设计规范(试行)[S].北京:中国铁道出版社,2010.

[5]中华人民共和国住房和城乡建设部.GB 50009—2012 建筑结构荷载规范[S].北京:中国建筑工业出版社,2012.

[6]金新阳.建筑结构荷载规范理解与应用[M].北京:中国建筑工业出版社,2013:157-169.

[7]中华人民共和国住房和城乡建设部.GB 50153—2008 工程结构可靠性设计统一标准[S].北京:中国计划出版社,2009.

[8]欧祖敏,孙璐,程群群.基于气象资料的无砟轨道温度场计算与分析[J].铁道学报,2014,36(11):106-112.

OU Zumin,SUN Lu,CHENG Qunqun.Analysis on Temperature Field of Ballastless Track Structure Based on Meteorological Data[J].Journal of the China Railway Society,2014,36(11):106-112.

[9]欧祖敏,孙璐,程群群.高速铁路无砟轨道温度场简化计算方法[J].浙江大学学报:工学版,2015,49(3):482-487.

OU Zumin,SUN Lu,CHENG Qunqun.Simplified Calculation of Temperature Field in High-speed Railway Ballastless Track Structure[J].Journal of Zhejiang University:Engineering Science,2015,49(3):482-487.

[10]BS E N 1991-1-5:2003.1-5 Eurocode 1:Action on Structures-Part 1-5 General Actions-Thermal Actions[S].2003.

[11]白国良,薛建阳,吴涛.工程荷载与可靠度设计原理[M].北京:中国建筑工业出版社,2012:138-148.

[12]NAESS A,GAIDAI O.Estimation of Extreme Values from Sampled Times Series[J].Structural Safety,2009,31:325-334.

[13]赵国藩，曹居易，张宽权.工程结构可靠度[M].北京:科学出版社,2011:80-88.

[14]RUSZCZAK B,TOMASZEWSKI M.Extreme Value Analysis of Wet Snow Loads on Power Lines[J].IEEE Transactions on Power Systems,2015,30(1):457-462.

[15]史道济.实用极值统计方法[M].天津:天津科学技术出版社，2006:30-52.

[16]曹振华，赵平.概率论与数理统计[M].南京:东南大学出版社，2004:103-112.

[17]国家技术监督局，中华人民共和国建设部.GB 50216—1994 铁路工程结构可靠度设计统一标准[S].北京:中国计划出版社,1995.