基于引力搜索RBF神经网络的机车齿轮箱故障诊断

卫晓娟，丁旺才，李宁洲，郭文志

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

齿轮箱是机车牵引传动系统中一个非常重要的部件，其故障的精确诊断对于提高机车牵引传动系统检修质量、保障机车有效发挥牵引性能及列车安全运行至关重要。传统的机车齿轮箱故障诊断主要是依靠工作人员的经验对故障进行主观判断，对工作人员的经验要求较高，但其诊断效率较低，已经不能满足机车状态修(即视情维修)的要求[1]。神经网络和智能计算等人工智能技术可使机器能够胜任一些通常需要人类智能才能完成的复杂工作，其在铁道机车车辆设备故障诊断中也得到了成功运用[2-4]。因此，如能有效利用人工智能技术对检修数据进行分析处理以准确判断机车齿轮箱故障，对于指导维修实践、提高检修质量、减轻工作人员工作负荷、降低对人员技术水平与工作经验的要求具有重要的实际工程价值。

神经网络作为实现多属性故障诊断的一种有效方法，具有处理分布不均匀、线性不可分复杂数据的能力，因此适用于解决具有故障原因较多且各种因素相互耦联导致故障与征兆之间的映射关系呈现非确定性及复杂非线性特点[5]的机车齿轮箱故障诊断问题。然而神经网络的结构及参数的确定尚无规律可循，若参数选择不当则会使其在故障诊断中存在明显不足。因此，将神经网络引入机车齿轮箱的故障诊断需要解决两个关键问题：网络结构的确定及网络参数的优化选择。现有相关文献虽有将神经网络用于解决机车车辆齿轮箱故障诊断的研究[6，7]，但关于网络结构的确定及网络参数的优化选择却鲜有涉及。

基于此，本文提出一种基于引力搜索RBF神经网络的机车齿轮箱智能故障诊断方法，建立基于高斯RBF神经网络的机车齿轮箱故障诊断模型，采用减聚类算法[8]确定RBF神经网络的结构，并提出自适应混合引力搜索算法(Adaptive Hybrid Gravitational Search Algorithm，简称AHGSA算法)对故障诊断模型的待优化参数进行优化求解。利用国际标准测试数据集对该方法进行仿真实验，并将该方法应用于某机务段机车齿轮箱故障的诊断中，验证了该方法在工程应用中的有效性和可行性。

1 机车齿轮箱故障诊断模型的建立

1.1 机车齿轮箱故障类型与故障征兆分析

机车齿轮箱的主要故障有：齿轮啮合时因润滑不良或齿面存在入侵的微小金属颗粒和粉尘而使齿面发生磨粒磨损；因润滑油提供不足及颗粒和粉尘等异物入侵而导致轴承工作面无法形成有效的油膜，引起轴承表面磨损；因保持架老化及滚动体向外挤压作用而发生的轴承保持架磨损；因高速运行时油液飞溅到箱体而发生的齿轮箱箱体磨损；齿轮箱密封不良等[5]。

大量故障实例表明，机车齿轮箱发生上述故障时会导致润滑油中所含机械磨屑和其他微粒的形态、大小、成分、浓度和粒度分布等发生变化，如：齿面磨粒磨损和轴承表面磨粒磨损会使铁(Fe)及铬(Cr)、铅(Pb)等元素的浓度上升；轴承保持架磨损会使铜元素(Cu)浓度上升；齿轮箱箱体磨损会使铝元素(Al)浓度上升；齿轮箱密封不良则会使硅元素(Si)浓度上升。因此，通过对润滑油进行定性分析与定量测量，即可得到摩擦副磨损状况等重要信息。

原子发射光谱技术和铁谱分析技术是铁路机务部门检测机车齿轮箱故障征兆的主要手段，其实质就是通过对润滑油进行油品分析以获得油中磨损元素的含量。通过对机务部门监测得到的光铁谱数据进行分析处理，可建立机车齿轮箱不同磨损故障的故障样本库。

1.2 机车齿轮箱故障诊断模型

基于高斯RBF神经网络建立机车齿轮箱故障诊断模型时，首先将故障样本数据及故障模式的对应数值均映射到[0，HR]区间，其中HR∈R1，以使数据点的每一维(即样本所有属性值)和故障模式数值都介于[0，HR]之间，然后依据样本维数确定网络输入层节点数，并采用减聚类算法确定网络隐层节点数，网络输出层则选定为1个节点。

假设待诊断样本为S=(f1，f2，…，fs，)，s为样本数据维数，则机车齿轮箱故障诊断模型可以表示为

j=1，2，…，s

( 1 )

式中：Ftype表示故障类型；h为网络隐层节点数；w为连接隐层和输出层的权值；c为隐层节点中心；σ为径向基函数宽度；Ftype-s为故障模式映射到[0，HR]区间的数值。

该模型通过计算RBF神经网络实际输出值与故障模式映射到[0，HR]区间的对应数值之间的误差，实现故障类型的准确判断，误差最小或满足相应精度要求的故障模式即为待诊断样本对应的故障类型。模型优化求解时，w、σ和c作为待优化参数。

2 机车齿轮箱故障诊断模型的优化

机车齿轮箱故障诊断模型的优化实质上是一个多维参数空间上的寻优问题，其优化效果与优化算法的性能密切相关。本文提出AHGSA算法对机车齿轮箱故障诊断模型进行优化求解。

2.1 自适应混合引力搜索算法

引力搜索算法虽然具有相对较强的全局探索能力，但其局部开发能力较差，为了实现全局探索能力和局部开发能力的平衡，本文提出的自适应混合引力搜索算法从种群初始化、速度和位置更新方式、万有引力系数调整三个方面对引力搜索算法进行改进。

2.1.1 引力搜索算法

引力搜索算法是伊朗科尔曼大学的Rashedi等于2009年提出的一种全局随机搜索算法[9，10]。该算法中，粒子的位置表示待优化问题的解。粒子因受到群体中其他粒子的万有引力作用而产生加速度，从而改变粒子的速度和位置。

( 2 )

式中：Mi(t)和Mj(t)分别表示t时刻粒子i和粒子j的惯性质量；ε为一个很小的正常数；G(t)为t时刻的万有引力系数，其计算公式为

( 3 )

式中：G0和α为常数；maxiter为最大迭代次数。

粒子i的惯性质量定义为

( 4 )

式中：mi(t)为计算粒子惯性质量的中间变量，其计算公式为

( 5 )

式中：fi(t)是t时刻粒子i的适应值；fworst(t)和fbest(t)分别是t时刻所有粒子中最差的适应值和最好的适应值。

( 6 )

基于牛顿第二定律，可计算出t时刻粒子i在第d维空间上的加速度为

( 7 )

式中：randj是一个[0，1]之间的随机数，kbest是对粒子i产生引力的粒子的集合。

则t+1时刻粒子i的速度和位置更新公式为

( 8 )

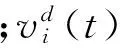
2.1.2 混沌序列初始化策略

优化算法通常通过随机方式产生初始种群，若初始种群的多样性和对解空间搜索的遍历性不利于搜索到待优化问题的全局最优解时，则需要增加迭代次数或种群大小来获得最优解，这势必影响优化算法的搜索效率和稳定性。而遍历性和随机性是混沌运动的典型特征，因此采用混沌序列初始化种群，有利于提高种群的多样性和粒子搜索的遍历性。文献[11]通过分析指出Tent模型比Logisitic映射具有更好的遍历性和更高的搜索效率，并验证了Tent模型在增加种群多样性以及改善算法寻优性能方面的有效性。因此，本文采用Tent模型进行种群的混沌序列初始化操作。

Tent模型的表达式为

Tk+1=G(Tk)k=0，1，…，N-1

( 9 )

其中

(10)

假设种群规模为n，变量的维数为M维。种群初始化时，首先随机产生一个M维，且每个分量数值在[0，1]之间的向量T1=(T11，T12，…，T1M)，然后将其代入式( 9 )，经过N次(N>n)迭代产生一个包含N个向量T1，T2，…，Tm，…，TN的混沌序列，再将Tm(m=1，2，…，N)的各个分量经映射xmk=xkmin+(xkmax-xkmin)Tmk(k=1，2，…，M)转化到对应变量的取值区间，构成包含N个初始粒子的群体，再通过比较这N个粒子的适应值，从中选出适应值相对较小的n个解作为初始解，此即为种群的初始位置。

2.1.3 基于人工蜂群搜索算子的变异操作

文献[12]对文献[13]提出的人工蜂群算法中的搜索算子进行改进，提出了如式(11)所示的人工蜂群搜索算子。

(11)

(12)

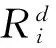
λ(t)=pt

(13)

式中：t为迭代次数；p为等比系数，且p∈(0，1)。

构造变异算子后，将其与速度、位置分别进行组合，得到t+1时刻粒子i的速度和位置更新公式为

(14)

2.1.4 万有引力系数的自适应调整

较大的万有引力系数可以增强算法的全局搜索能力，而较小的万有引力系数则可以增强算法的局部搜索能力。寻优过程中，性能越优的粒子，全局最优解出现在其周围的概率越大，因而万有引力系数应较小，以使这部分粒子的运动速度较小，从而保证其能够进行局部精细搜索；反之，性能相对较差的粒子，全局最优解出现在其周围的概率较小，万有引力系数应较大，以使这部分粒子的运动速度较大，从而保证其能够进行全局搜索。

基于上述分析，AHGSA算法根据粒子性能对万有引力系数进行自适应调节，以使算法的全局探索能力和局部开发能力得到平衡，从而提高算法的整体寻优效率。为此，按比例φ(φ在[0，30%]之间随进化代数递增)选择适应值相对较差的粒子，对其万有引力系数G进行调节，即令

G=G0

(15)

而对性能相对较优的粒子(即适应值相对较小的粒子)，仍按式( 3 )计算G。

2.2 基于AHGSA算法的故障诊断模型优化

(16)

采用AHGSA算法使式(16)取得最小值的全局最优解即是故障诊断模型的最优参数w、σ和c。其求解流程如图1所示。

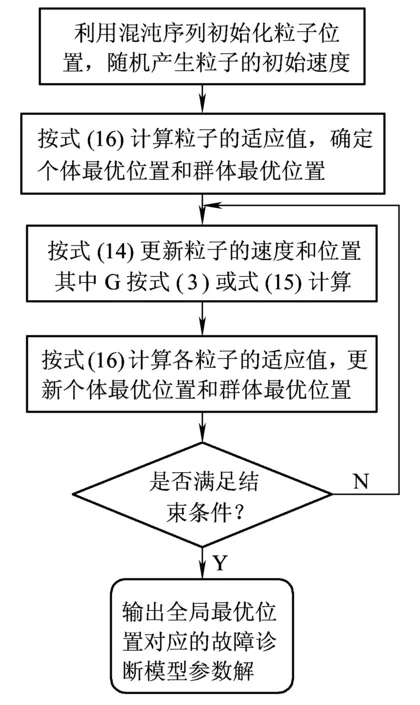
图1 故障诊断模型求解流程

3 基于引力搜索RBF神经网络的故障诊断

3.1 引力搜索RBF神经网络的性能测试

为了测试引力搜索RBF神经网络对非线性问题的分类性能，选取了Iris和Wine两组UCI测试数据集进行实验。在相应的标准样本集中选择全部样本作为训练样本，随机抽取部分样本作为测试样本。通过训练样本建立诊断分类模型，测试样本测试分类准确性。

测试数据集的基本信息见表1。其中，Iris分为三种，每种有四种属性：萼片长度、萼片宽度、花瓣长度和花瓣宽度，三种Iris各有50组数据，共有150组数据；Wine分为三种，每种有酒精度、苹果酸、灰末等13种属性，三种Wine共有178组数据。

表1 测试数据集基本信息

利用经遗传算法(简称GA)、粒子群算法(简称PSO)、量子粒子群算法(简称QPSO)、引力搜索算法(简称GSA)和AHGSA优化的RBF神经网络分别对上述测试数据集进行分类实验。根据Iris属性选定输入层为4个节点，输出层为1个节点；根据Wine属性选定输入层为13个节点，输出层为1个节点；采用减聚类算法确定隐层节点数为6个。GA算法参数为：交叉概率0.6，变异概率0.4(其中0.2随机变异，0.2为高斯变异)；PSO算法参数为：认知系数c1和社会系数c2设置为c1=c2=2，惯性权重w设置为在[0.9，0.4]之间线性递减；QPSO算法参数为：收缩扩张系数β设置为在[0.5，1]之间线性递减；GSA算法参数为：G0=100，α=14；AHGSA算法参数为：G0=140，α=17，等比系数p=0.95。五种方法进行Iris数据集分类时种群规模为200，Wine数据集分类时种群规模为300，进化代数均为600。

五种方法对Iris和Wine数据集的分类结果见表2。从表2不难发现，经自适应混合引力搜索算法优化后的RBF神经网络分类精度更高，泛化能力较强，其在高维非线性分类问题上的性能明显优于采用其他四种算法优化的RBF神经网络。

3.2 机车齿轮箱故障诊断

将本文方法分别应用于某机务段两种不同类型机车的齿轮箱故障征兆的光铁谱数据[4]分类诊断中，以验证该方法在工程应用中的实用性和可行性。故障样本的特征量为14个：大磨粒浓度，小磨粒浓度，磨损磨粒总浓度，以及Fe、Cr、Pb、Cu、Zn、Al、Si、B、Na、Ca、P元素的浓度等故障征兆属性，分别用f1～f14表示。故障类型分别为齿轮磨损、轴承磨损、密封不良、保持架磨损和齿轮箱箱体磨损。

3.2.1 诊断实例一

采用本文方法对东风4D型机车齿轮箱故障的光铁谱数据进行诊断，部分故障样本见表3。

表2 不同方法的分类精度对比

表3 故障样本

根据故障样本属性，确定RBF神经网络输入层为14个节点，输出层为1个节点，采用减聚类算法确定隐层节点数为7个。AHGSA算法参数为：G0=140，α=17，等比系数p=0.95，种群规模为300，进化代数为1 000。将样本数据的每一维都映射到[0，1.2]区间，采用本文方法进行故障诊断时，故障诊断模型的输出数据在[0，0.2]区间对应为正常状态，输出数据在[0.2，0.4]区间对应为齿轮磨损，输出数据在[0.4，0.6]区间对应为轴承磨损，输出数据在[0.6，0.8]区间对应为密封不良，输出数据在[0.8，1.0]区间对应为保持架磨损，输出数据在[1.0，1.2]区间对应为齿轮箱箱体磨损。

机车齿轮箱故障诊断模型参数优化时，σ和c的取值范围均为[0，1]，w的取值范围为[-50，50]，AHGSA算法在式(16)所示目标函数的引导下，在参数空间搜索寻优，达到结束条件(即预设的最大进化代数)时的群体最优位置Pg即为模型参数的优化值。表4为机车齿轮箱故障诊断模型的优化参数，图2为其中三个参数(第6个隐节点的宽度，即σ(6)；第1个隐节点的第10个中心，即c(1，10)；连接第7个隐节点与输出的权值，即w(7))的收敛曲线，出于篇幅的考虑，其余参数的收敛曲线不再列出。

表4 故障诊断模型参数

随机选取3组测试样本，分别为S1=(75.7，40.5，116.2，249.4，1.8，0.2，6.9，8.5，16.2，53.5，244.8，2，5.5，1 218)，S2=(86.2，71.5，157.7，621.3，3.2，2.1，12.5，94.1，44.4，44.1，197.5，2，4.8，1 351)，S3=(97.6，59.5，157.1，234.4，0.91，1.21，8.73，11.5，77.8，40.9，255.1，2，7.13，1 229)，采用本文方法进行诊断，诊断结果见表5。其中，将样本S1诊断为正常状态，将样本S2诊断为齿轮磨损，将样本S3诊断为齿轮箱箱体磨损，诊断结果与实际情况相符。

图2 模型参数的收敛曲线

样本模型输出结果诊断结果S10.099906正常S20.300063齿轮磨损S31.100550齿轮箱箱体磨损

3.2.2 诊断实例二

采用本文方法对HXD1C机车齿轮箱故障的光铁谱数据进行诊断测试，故障测试样本见表6。故障诊断模型参数与表4所示参数相同。将测试样本输入诊断模型，诊断结果见表7。其中，将1号样本诊断为正常，2号样本诊断为齿轮磨损，3号样本诊断为轴承磨损，4号样本诊断为密封不良，5号样本诊断为保持架磨损，6号样本诊断为齿轮箱箱体磨损。诊断结果与实际情况一致。

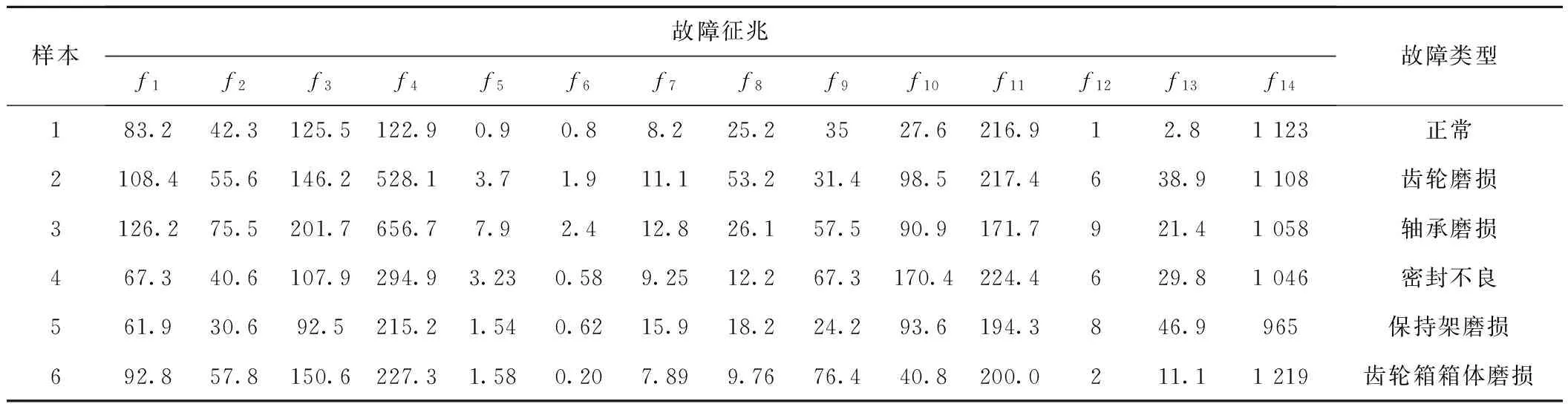
表6 故障样本

表7 诊断结果

通过故障诊断实例不难发现，本文所提出的故障诊断方法能够自适应优化机车齿轮箱故障诊断模型的参数，从而使得故障分类结果更为客观合理，有效保证了故障诊断精度。经过训练得到的RBF神经网络故障诊断模型可实现相应故障的实时诊断。

4 结论

针对神经网络在机车齿轮箱故障诊断中存在的问题，本文基于RBF神经网络建立了机车齿轮箱故障诊断模型，并提出自适应混合引力搜索算法求解模型参数，测试实验结果表明，该算法具有良好的寻优精度和效率，在满足相应目标函数取得最小值的情况下，能够求解出相对最优的模型参数。机车齿轮箱故障诊断实例也表明，本文方法具有处理分布不均匀、线性不可分的复杂故障数据的能力，能够有效分离故障特征。本文研究成果为机车齿轮箱故障诊断提供了新的思路和方法。

参考文献：

[1]杨江天,周培钰.经验模态分解和Laplace小波在机车柴油机齿轮系故障诊断中的应用[J].机械工程学报,2011,47(7)：109-115.

YANG Jiangtian,ZHOU Peiyu.Fault Diagnosis for Gear Train of Locomotive Diesel Engine Based on Empirical Mode Decomposition and Laplace Wavelet[J].Journal of Mechanical Engineering,2011,47(7)：109-115.

[2]董锡明.机车车辆测试性与技术诊断[J].铁道机车车辆,2006,21(1)：44-54.

DONG Ximing.Testability and Technique Diagnosis for Locomotive and Car[J].Railway Locomotive and Car,2006,21(1)：44-54.

[3]黄志武,宾睿,杨迎泽,等.CCBⅡ制动机系统模式追踪与多故障诊断技术[J].铁道学报,2014,36(3)：68-74.

HUANG Zhiwu,BIN Rui,YANG Yingze,et al.Mode Tracking and Multiple Faults Diagnosis of CCBⅡ Brake System[J].Journal of the China Railway Society,2014,36(3)：68-74.

[4]付强,陈特放,朱佼佼.基于HPSO-WNN的牵引变压器故障诊断算法研究[J].铁道学报,2012,34(9)：26-32.

FU Qiang,CHEN Tefang,ZHU Jiaojiao.Research on Traction Transformer Faults Diagnosis Algorithm Based on HPSO-WNN[J].Journal of the China Railway Society,2012,34(9)：26-32.

[5]程瑞琪,周美玉.基于统计与时间序列的内燃机车机油光谱数据分析与故障诊断[J].铁道学报,1999,21(4)：20-24.

CHENG Ruiqi,ZHOU Meiyu.Statistics and Time Series Based Spectrographic Oil Analysis Data Processing for Locomotive Diesel Engine Wear Diagnosis[J].Journal of the China Railway Society,1999,21(4)：20-24.

[6]李刚,范万里,姜海莲,等.结合光铁谱技术用神经网络诊断电力机车齿轮箱故障[J].机械传动,2013,37(3)：78-82.

LI Gang,FAN Wanli,JIANG Hailian,et al.Fault Diagnosis of Electric Locomotive Gearbox by Using Combination RDEAES and Ferrography and Neural Network[J].Journal of Mechanical Transmission,2013,37(3)：78-82.

[7]齐振国,侯秀娟.神经网络在铁道车辆齿轮箱故障诊断系统中的应用[J].机车电传动,2014(1)：97-99.

QI Zhengguo,HOU Xiujuan.Application of Neural Network in Railway Vehicle Gearbox Fault Diagnosis System[J].Electric Drive for Locomotive,2014(1)：97-99.

[8]CHEN J Y,QIN Z,JIA J.A PSO-based Subtractive Clustering Technique for Designing RBF Neural Networks[C]//Proceedings of the 2008 Congress on Evolutionary Computation.Hong Kong：IEEE Press,2008：2 047-2 052.

[9]RASHEDIE,NEZAMABADI-POUR H,SARYAZDIS.GSA：A Gravitational Search Algorithm[J].Information Sciences,2009,179(13)：2 232-2 248.

[10]RASHEDIE,NEZAMABADI-POUR H,SARYAZDIS.BGSA：Binary Gravitational Search Algorithm[J].Natural Computing,2010,9(3)：727-745.

[11]张浩,张铁男,沈继红,等.Tent 混沌粒子群算法及其在结构优化决策中的应用[J].控制与决策,2008,23(8)：857-862.

ZHANG Hao,ZHANG Tienan,SHEN Jihong,et al.Research on Decision-makings of Structure Optimization Based on Improved Tent PSO[J].Control and Decision,2008,23(8)：857-862.

[12]ZHU G P,KWONG S.Gbest-guided Artificial Bee Colony Algorithm for Numerical Function Optimization[J].Applied Mathematics and Computation,2010,217(7)：3 166-3 173.

[13]KARABOGA D,BASTURK B.On the Performance of Artificial Bee Colony(ABC) Algorithm[J].Applied Soft Computing,2008,8(1)：687-689.