On the Quadratic Twists of Gross Curves

LI Kezheng,　REN Yuan

(Department of Mathematics, Capital Normal University, Beijing 100037)



On the Quadratic Twists of Gross Curves

LI Kezheng,REN Yuan

(DepartmentofMathematics,CapitalNormalUniversity,Beijing100037)

Abstract：In this paper, we use 2-descent method to compute the 2-Selmer group for some twists of the elliptic curves constructed by Gross. As a result, we can verify the BSD conjecture for some of them by combining results about L-values.

Key words：complex multiplication; descent; BSD; graph

2010 MSC：11G05; 11G15

1Introduction

The arithmetic of elliptic curves over a number field has been an area of great interests in number theory.LetEbe an elliptic curve defined over a number fieldF. The Mordell-Weil theorem tells us thatE(F) is a finitely generated abelian group, but it is usually difficult to determine the rank (called Mordell-Weil rank). One can estimate the rank by computing various Selmer groups, for example the 2-Selmer groups.

In [1-2], for the congruent elliptic curveE(n):y2=x3-n2xwith rational integern, Feng gave some conditions for when the 2-Selmer group is the smallest, i.e. the 2-Selmer group is just the 2-torsion points. In recent years, much effort have been devoted to the study of the congruent number elliptic curveE:y2z=x3-xz2[3-4]. In particular, Y. Tian[5-6] has made a breakthrough .

In this paper, we will study a similar question for the elliptic curves considered by Gross in [7]. LetKbe an imaginary quadratic extension of the rational fieldQ,andHbeitsHilbertclassfield.AnellipticcurveEdefinedoverHwithcomplexmultiplication(CMforshort)byO=OKiscalledaQ-curve if for anyσ∈ Gal(H/Q),EσisH-isogenous toE.

suchthat

and any two of them differs from an action of Gal(H/K).

Let

then it corresponds to anH-isogeny class [C] ofQ-curveswithCMbyOK. This is theQ-curvesconsideredin[7].Itiseasytoseetheconductorofχpisπandforanyrationald,theconductoroftheassociatedcharacterof[C(d)]islargerthanπ.

In[7],Grossestablishedthebasicpropertiesofthesecurves.Inparticular,heobservedthatonecanintroduceanaturalactionofGal(H/K)ontheSelmergroupsandthenreducesomecalculationfromHtoK (wewillbrieflyexplainthisinthenextsection).HealsocomputedSel2(E/H)Gal(H/K)forE∈[C],andshowedE(H)=E[2].

Inthispaper,wewillcomputeSel2(E(d)/H)Gal(H/K)foralltheintegersdsuchthatd≡1(mod4),whereE(d)isthetwistofEbyd (in[8]).

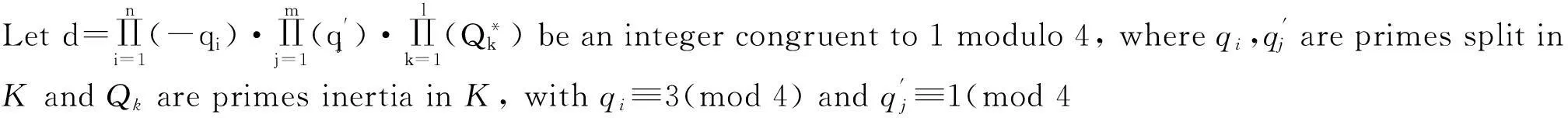
Leth=hKbe the class number ofK, then

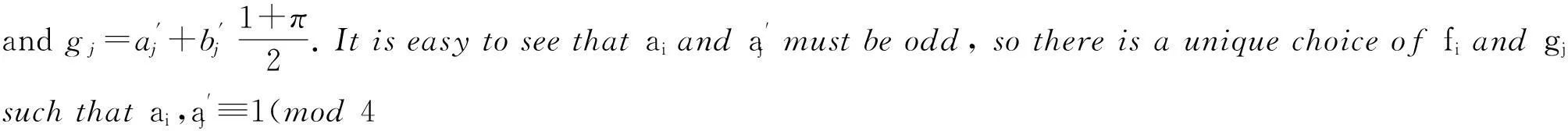
Definition1.1Letd≡1(mod4)andfi,gj,Qkasabove.

Definea(oriented)graphGasfollowing:

Vertexof

Recallthatagraphiscalledanoddgraphifeachnon-trivialpartitionofitisanoddpartition.Themainresultis

Theorem1.2Foreveryd≡1(mod4),wehave

wheretis the number of even partitions ofG.

In particular,S(d)is minimal if and only ifGis an odd graph.

We will prove this theorem in the third section after reviewing the descent method in the next section. Then we will give some numerical examples and discuss some consequences related to the BSD conjecture.

Note that elliptic curves over finite field is useful in designing cryptograph, see for example [9] and [10]. It is hoped that the results here will also be useful in such problems.

2Descent method forQ-curves

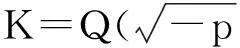
Firstweintroducethefollowingnotations:

K=animaginaryquadraticextensionoverQ;

O=theintegerringofK;

ELL(O)={ellipticcurveoverCwithCMbyO } up to C-isomorphism;

H= the Hilbert class field ofK;

ELLH(O)={elliptic curve overHwith CM byO}uptoH-isomorphism;

Recall the following basic facts from CM theory, in [7]:

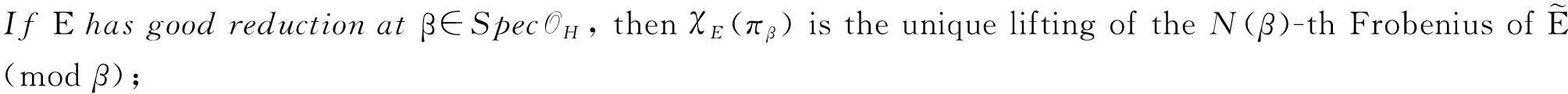
(iii) for any rational primel,wehave

We now review theH-isomorphic andH-isogenous classifications of elliptic curves with CM byO.

(i) There is a bijection

(ii)Thereisabijection

Lemma2.3ForanyE∈ELLH(O)andψ:GH→O×a continuous homomorphism, letEψdenote twist ofEbyψ(note thatO×=Aut(E)),then

LetwbeaplacewhereχEψ, ψ·χEandψareallunramified.Thenfromψσ(w)=φ-1∘φσ(w),wehave

Sothatasmorphism,wehave

whichimpliesthatψσ(w)·χE(w)=χEψ(w)byactingontheinvariantdifferential.

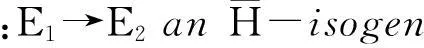
ThenχE2=ψ·χE1.

ProofAsintheproofofLemma2.3,forallbutfinitelymanyw,because

whichmeans

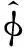
thenwehaveχE2=ψ·χE1.

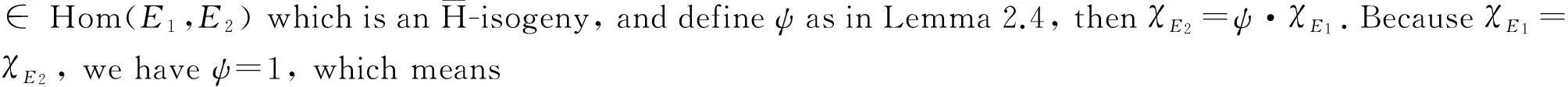
Recall the definition ofQ-curves:

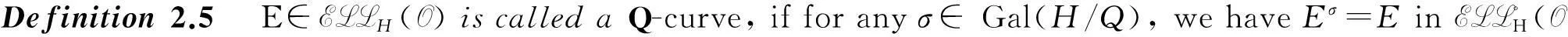
We will now describe the descent method used in [7].

Lemma 2.6LetE∈ELLH(O) be aQ-curve.Thenforanyσ∈Gal(H/Q),

Hom(Eσ,E)/2Hom(Eσ,E)≅O/2O.

ProofAssumeE[2]isgeneratedbyPoverO/2O,soEσ[2]isgeneratedbyPσ.Forany

let[aφ]∈O/2Osuchthat

thisgivesahomomorphism

which is obviously injective. On the other hand, the density theorem implies that this homomorphism is surjective.

Recall that from

we get the following diagram (Fig.1)：

0→E(H)/2E(d)(p)δ→H1(GH,E[2])→H1(GH,E[2])→0↓↓↓0→∏E(Hv)/2E(d)(p)(Hv)δv→∏H1(GHv,E[2])→∏H1(GHv,E[2])→0

Fig. 1

Definition 2.7Define the Selmer group

Sel2(E/H)=

{x∈H1(GH,E[2]):Resv(x)∈im(δv),forallplacesv},

and the Tate-Shafarevich group

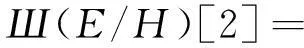
For anyQ-curvesE,wecangiveE(H)/2E(H),Sel2(E/H)andШ(E/H)[2]astructureofGal(H/Q)-modulebyusingLemma2.6asfollowing,

(i)Foranyσ∈Gal(H/K)and

define

whereφ∈Hom(Eσ,E)ischosensothatφmapsto1undertheisomorphisminLemma2.6;

(ii)Foranyσ∈Gal(H/K)andx∈Sel2(E/H),define

whereφ∈Hom(Eσ,E)ischosensothatφmapsto1undertheisomorphisminLemma2.6;

(iii)Foranyσ∈Gal(H/K)andx∈ Ш(E/H)[2],define

whereφ∈Hom(Eσ,E)ischosensothatφmapsto1undertheisomorphisminLemma2.6.

Itiseasytoverifytheaboveactionsareindependentofthechooseofφ.

Proposition2.8Theexactsequence

is an exact sequence of Gal(H/Q) modules.

ProofIt is enough to showδis a homomorphism of Gal(H/Q)-modules.

For anyP∈E(H)/2E(H), assume [2]Q=P, thenδ(P)(g)=Qg-Q, for anyg∈GH. Chooseφ∈Hom(Eσ,E) such thatφ≡1(2), then we have by definitionσ(P)=φ(Pσ), so

the proposition then follows.

RemarkIt is easy to see that all the results in this section hold forE(H)/ωE(H), Selω(E/H) and Ш(E/H)[2] for anyω∈O.ItisinterestingtoknowtheGal(H/K)-modulestructureofE(H)/ωE(H),Selω(E/H)andШ(E/H)[2]foranyω∈O.

3Main thoerem

Proposition 3.1 Notation as above and let [C] be the isogeny class corresponding theχpin section 1, we have:

(i) For anyE∈[C] andda rational integer prime top, letF=Q(j(E)), then the root number ofL(E(d)/F,s) is the sign ofd;

(ii) For anyE∈[C] andda rational integer prime top, we haveE[2]=E(H)tor;

(iii) Under the action of Gal(H/K), we have

with some integern(d), so that

Inparticular,wehave

Lemma 3.2 For anyE1,E2∈[C], we have

Sel2(E1/H)≅Sel2(E2/H)

as Gal(H/K)-modules.

ProofAsEi[2]⊆Ei(H), we have

sendingψ∈ Hom(GH,E1[2]) toφ∘ψ. We know from Proposition 3.1 thatEi[2] are trivial Gal(H/K)-modules. So for anyψ∈ Hom(GH,E1[2]),g∈GHandσ∈ Gal(H/K), we have

i.e.ψis a homomorphism of Gal(H/K)-modules. And this gives the desired homomorphism between Sel2(E1/H) and Sel2(E2/H).

In the following, we writeS(d)for

By Lemma 3.2, we only need to computeS(d)for any fixedE∈[C]. But we have the following.

Lemma 3.3There is a uniqueE(p) overFwith

Proof[7]We will do the computation for thisE(p).Recall that from

we get the following diagram (Fig.2)：

0→E(d)(p)(H)2E(d)(p)δ→H1(GH,E(d)(p)[2])2→H1(GH,E(d)(p))[2]→0↓↓0→∏E(d)(p)(Hv)2E(d)(p)(Hv)δv→∏H1(GHv,E(d)(p)[2])→∏H1(GHv,E(d)(p))[2]→0

Fig. 2

Lemma 3.4 There is a basis ofE(d)(p)[2], such that

for all placesvofHoverω, and

wehave

which is even. If 2|y, then 2│/xbecause 2│/fω, then

is odd which is a contradiction, so 2│/yandavis odd. Now it follows thatE(p)(d)has good ordinary reduction because its character differs fromχpby a quadratic character unramified over 2.

From [11], Lemma 3.5, there is a unique two torsion pointP1such thatP1≡O(modω).Because

Tostatetheresults,weintroducethefollowingnotations.

Let

Lemma3.5Fromthenotationasabove,wemayassume

withai≡1(mod 4) andv2(bi)=1;

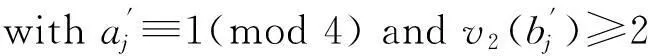
is odd, so it is easy to see that 2│/aibut 2|bi, and hence we can multiply it by ±1 so thatai≡1(mod 4).

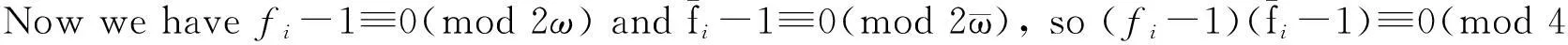
becausehis odd by the genus theory, so

i.e.bi+2(ai-1)≡2(mod 4), then we havebi≡2(mod 4).

The proof for the second assertion is similar.

Lemma 3.6 Letd≡1(mod 4) be an integer and notations as above,then we have

(i)E(d)(p) has good reduction at all the places not dividingpd;

(ii) There is a basis ofE(d)(p)[2], such that

wherea,…,vk′=0 or 1;

(iii) For anyv│/ 2, we have #im(δv)=4.

Proof(i) This is becauseE(p) only has bad reduction at the places overpanddis congruent to 1 mod 4;

(ii) Note that by the genus theory, the order of Gal(H/K) is odd, so bothH1(Gal(H/K),E[2]) andH1(Gal(H/K),E[2]) are zero. Then by the Serre-Hoschild exact sequence, we have

and soS(d)⊆H1(GK,E[2]).

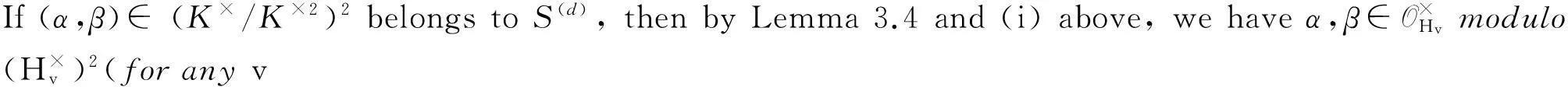
withai,…,vk=0,1 and similarly forβ.

(iii) Supposev│/ 2. By the theory of formal groups, there isM⊆E(d)(p)(Hv) such thatM≅OvandE(d)(p)(Hv)/Misfinite.Considerthefollowingdiagram(Fig.3):

0→M→E(d)(p)(Hv)→E(d)(p)(Hv)/M→02↓2↓2↓0→M→E(d)(p)(Hv)→E(d)(p)(Hv)/M→0

Fig. 3

Apply Snake Lemma, we get

Butasv│/ 2,thenwehave|Ov[2]|=|Ov/2Ov|=1 and the result follows;

(iv) Just by the definition of the Selmer group.

From Lemma 3.6 we know that to computeS(d), it is necessary to know the image ofE(d)(p)[2] underδ. For this, we have the following.

Lemma 3.7For anyd∈Z,thereisabasisofE(d)(p)[2]suchthat

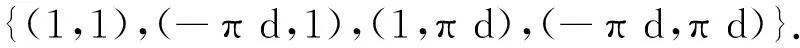
Andwehave

foranyv|pd.

ProofForthefirstassertion,itisenoughtoverifythisforthecased=1.FixthebasisasinLemma3.4.

TakeaWeierstrassequationoverHof

withΔ(E(p))=-p3.SinceE(p)haspotentiallygoodreductioneverywhere,wecanfindsomefiniteextensionofHsuchthatE(p)hasgoodreductionatπ.Thenachangeofcoordinatesoftheform

gives a Weierstrass equationE(p):f(X,Y)=0withgoodreductionatπ.NoticethatPi=(ei,0)’sarethe2-torsionpoints,wehave

andthenvπ(ei-ej)≥ 1.ButΔ(E(p))=-p3implies

hence we havevπ(ei-ej)=1.

By [8], Proposition 14, we have

Since Lemma 3.6 implies thatxi,yi≡(-1)aπbwitha,b=0 or 1, by combining the above results and Lemma 3.4, we have

For the second assertion, we note that the four elements

Now we can prove our main theorem which gives a complete description of the elements inS(d)ford≡1(mod 4).

Theorem 3.8 (α,β)∈S(d)is equivalent to (α,β)∈Hdand there is

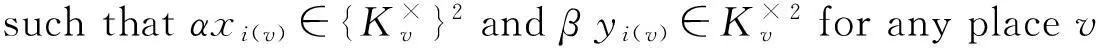
ProofThis follows from the definition of Selmer group, combining with Lemma 3.6 and Lemma 3.7.

In practice, one can always computeS(d)by Theorem 3.8 as the examples above. In the following, we give a graphical description of it, which seems more convenient to use.

Definition 3.9Letd≡1(mod 4) andfi,gj,Qkas in Lemma 3.5.

Define a (oriented) graphGas following.

vertex of

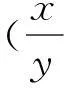
ProofofTheorem1.2DefinegraphG′withvertex

isanisomorphism,i.e.thereisanarrowfromxtoyifandonlyifthereisanarrowfromφ(x)toφ(y),whichisobvious.

4Numericalexamples

(iii)IfQ1andQ2areprimessuchthat

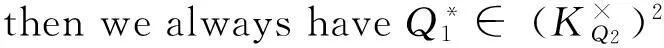
Proof(i) IfQis congruent to 3 modulo 4. By Hensel lemma, it is enough to solve

This is equivalent toa2-pb2≡0(Q) and

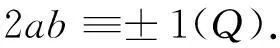
IfQiscongruentto1modulo4,then

so the equation doesn’t have any solutions.

(ii) This is well known ifQis congruent to 1 modulo 4. But (1) above implies this is also true forQcongruent to 3 modulo 4.

(iii) By Hensel lemma, it is enough to solve

ifandonlyifQi≡1(mod4)foranyi=1,…,n.

Moreover,wehaverankO/ 2OS(d)≥ 1+k, wherekis the number of thoseQiwhich is congruent to 3 module 4.

ProofIf all theQiare congruent to 1 module 4, we want to show that (α,β)∈S(d)implies (α,β)∈im(E(d)(p)[2]).

Suppose there is some (α,β)∈S(d)not in

then eitherα≠1,-πorβ≠1,π.

by Lemma 4.1. Now the claim follows from Lemma 3.6, (iv). This completes the first assertion.

By the above, we see that we always have

forQi≡3(mod 4). Since these elements are linearly independent inSd, we complete the proof.

Corollary 4.3Letdbe as in Proposition 4.2 withd>0 and

p>4d2lg|d|,

then the BSD conjecture is true forE(d)(p) and

In particular, we can construct arbitrarily large Shafarevich-Tate group by choosingplarge enough anddcontains enoughQwhich is congruent to 3 modulo 4.

ProofUnder the assumptions ond, we have

by the main theorem of [12]. So by the Coates-Wiles theorem (see [13]), we know that

and the assertions follows immediately from Theorem 1.2.

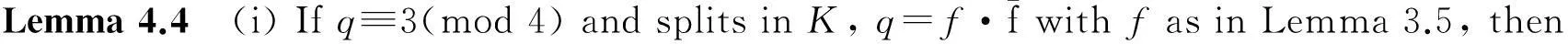
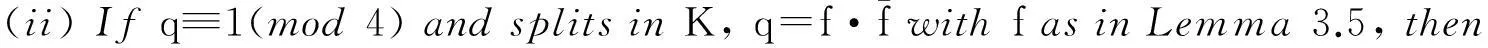
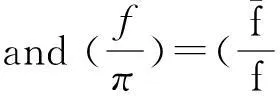
Proof(i)Write

thena≡1(mod 4) andv2(b)=1 as in Lemma 3.5.By Theorem 8.3 of [14], we have

But asf≡1(mod)ω2and

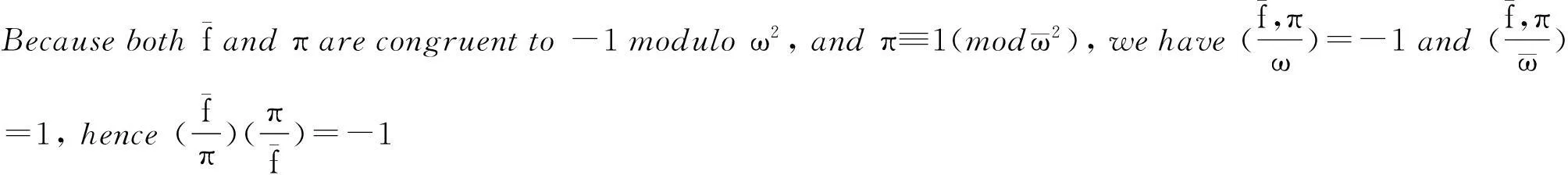
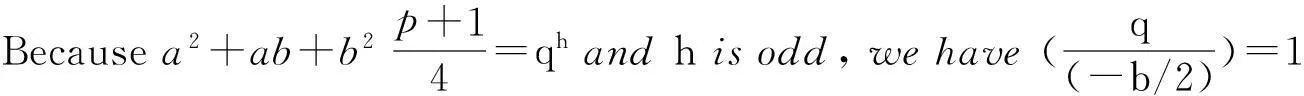
Because2|b,wehave

a2+ab≡1+ab≡qh(mod 8).

Thenifq≡3(mod8),wehaveb≡2(mod8);ifq≡7(mod8),wehaveb≡6(mod8),sothat

always holds. This finishes the proof of (i).

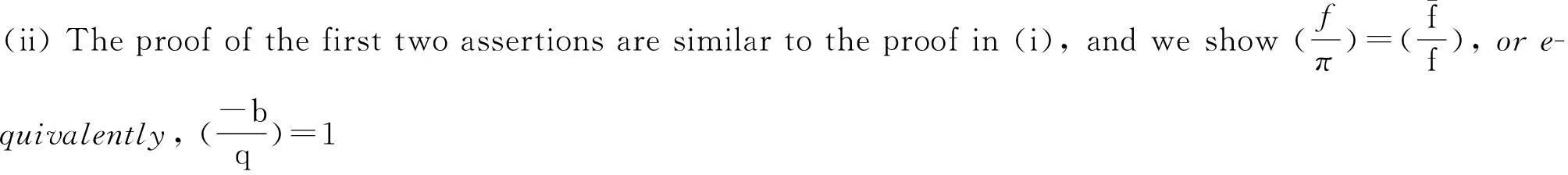
Assume|-b|=2ecwithcodd,then

Because

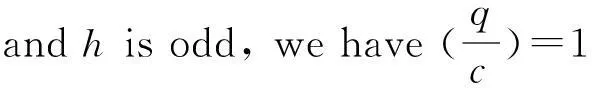
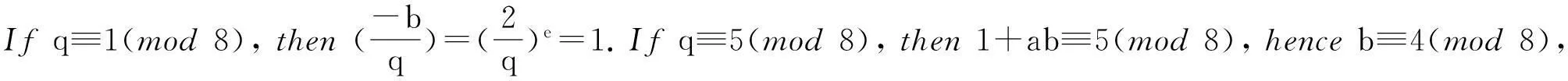
Proposition4.5Ifq≡3(mod4)splitsinK,then

rankO/ 2OS(q*)=3.

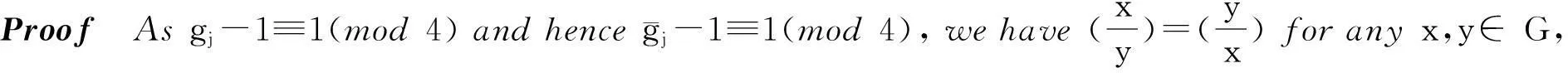
References

[1] 冯克勤. 非同余数和秩零椭圆曲线[M]. 合肥：中国科学技术大学出版社,2008.

[2] FENG K Q. Non-congruent number. odd graphs and the BSD conjecture[J]. Acta Arith,1996,75(1):71-83.

[3] 韩冬春. 关于椭圆曲线Ed2:y2=x3-d2x的BSD猜想[J]. 四川大学学报(自然科学版),2013,50(3):470-476.

[4] 佘东明. 关于椭圆曲线Ed2:y2=x3-d2x的Artin Root Number的计算[J]. 四川大学学报(自然科学版),2013,50(4):668-674.

[5] TIAN Y . Congruent numbers and Heegner points[J]. Cambridge J Math,2014,2(2):117-161.

[6] TIAN Y . Congruent numbers with many prime factoirs[J]. PNAS,2012,109(52):21256-21258.

[7] GROSS B. Atithmetic of Elliptic Curves with Complex Multiplication[M]. Berlin:Springer-Verlag,1980.

[8] SILVERMAN J H. The Arithmetic of Elliptic Curves (Graduate Texts in Mathematics)[M]. 2nd ed. New York:Springer-Verlag,2009.

[9] 廖群英,李俊. 有限域上Reed-Solomon码的一个注记[J]. 四川师范大学学报(自然科学版),2010,33(4):540-544.

[10] 廖群英,蒲可莉,叶亮节. 关于q元非对称纠错码[J]. 四川师范大学学报(自然科学版),2013,36(4):643-648.

[11] BRUMER A, KRAMER K. The rank of elliptic curves[J]. J Duke Math,1977,44(4):715-743.

[12] YANG T. Nonvanishing of certein Hecke L-series and rank of certein elliptic curves[J]. Composition Math,1999,117(3):337-359.

[13] COATES J, WILES A. On the conjecture of Birch and Swinnerton-Dyer[J]. Invent Math,1977,39:223-251.

[14] NEUKRICH J. Algebraic Number Theory[M]. New York:Springer-Verlag,1999.

[15] SERRE J. A Course in Arithmetic[M]. New York:Springer-Verlag,1973.

doi:10.3969/j.issn.1001-8395.2016.01.007

Received date:2015-08-27

Foundation Items:This work is supported by the National Key Basic Research 973 Program of China (2013CB834202)