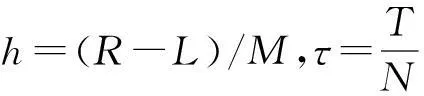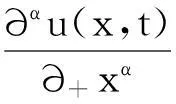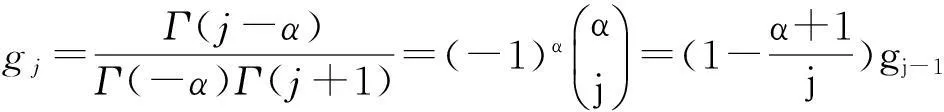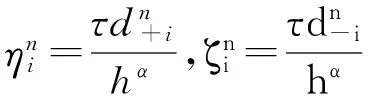两边空间分数阶对流-扩散方程的一种加权显式有限差分方法

马亮亮,　刘冬兵

(攀枝花学院 数学与计算机学院, 四川 攀枝花 617000)



两边空间分数阶对流-扩散方程的一种加权显式有限差分方法

马亮亮,刘冬兵

(攀枝花学院 数学与计算机学院, 四川 攀枝花 617000)

摘要：考虑两边空间分数阶对流-扩散方程的初边值问题,基于Grünwald公式和移位Grünwald-Letnikov公式,提出一种加权显式有限差分解法.利用傅里叶变换和特征值法,得到差分格式的稳定性.然后使用最大模估计法证明在相同的条件下,所提出的差分格式是收敛的.最后通过数值例子说明所提出的差分格式是可靠和有效的,并对方程的数值解与精确解进行比较,验证了文中的理论结果.

关键词：分数阶对流-扩散方程; 空间分数阶导数; 加权差分格式; 收敛性; 稳定性; 有限差分法

1预备知识

分数阶微分方程中含有非整数阶的导数,能够有效地描述各种各样物质的记忆和遗传性质,在工程、物理、金融、水文、地理、材料等领域发挥了愈来愈重要的作用[1-14].遗憾的是,大多数分数阶微分方程的解析解都含有复杂的级数或者特殊函数,不利于进行近似计算,于是对分数阶微分方程进行数值求解变得尤为重要.目前,许多学者致力于其中一类分数阶微分方程的-(时间、空间、空间-时间)分数阶对流-扩散方程的研究[15-23].

本文主要研究下列两边空间分数阶对流-扩散方程的数值解法

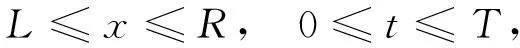
(1)

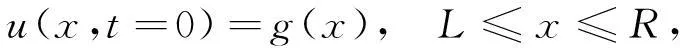
(2)

其中,0≤n-1<α

两边空间分数阶对流-扩散方程(1)是一种反常扩散方程,在地下水溶质运移方面,该方程可用来描述含水层中溶质运移过程中的反常扩散现象[24].关于这类问题的数值解法,前人已做了一些研究.苏丽娟等[24]给出了双边空间分数阶对流-扩散方程的一种隐式有限差分解法.M. Meerschaert等[25-26]分别对单边和双边对流-扩散方程利用改进型Grünwald-Letnikov差分方法进行了求解,但结果表明用Grünwald得到的显式差分格式是不稳定的,因此数值解不会收敛于方程的精确解.夏源等[27]对单边的时间和空间分数阶对流-弥散方程给出了类似的算法.F. Liu等[28]用此类算法对空间分数阶福克-普朗克方程进行了离散计算.马维元等[29]对空间-时间分数阶扩散方程的初边值问题提出了一种加权平均差分格式.张红玉等[30]给出了一类空间分数阶对流-扩散方程的加权平均有限差分解法.本文在标准Grünwald公式的基础上,利用移位Grünwald-Letnikov公式,构造出一种新的加权显式有限差分格式,并对其稳定性和收敛性进行理论分析,最后通过数值例子验证了该差分格式的有效性和可靠性.

2加权显式有限差分法

(5)

(6)

(7)

(9)

(10)

(9)～(10)式在时间和空间上都只有一阶精度,为了提高空间上的精度,对Grünwald公式和移位Grünwald-Letnikov公式进行加权处理得

于是得到下面的加权显式有限差分格式

(11)

其中,i=1,2,…,M-1,n=0,1,…,N-1;ε是权参数,且0<ε<1.

(12)

(13)

3稳定性和收敛性分析

定义 1对于任意的u∈R,(iu)α=sign(u)|u|αe(iπα)/2.

借助于定义1和2,对(14)和(15)式做傅里叶变换得

或

因此对任意的x∈R,|φ(x,h)|≤C3h2.

为半径的圆盘上,因此要使显式有限差分格(11)式稳定,需|λ-Ai,i|

现要使显式有限差分格(11)式稳定,只需证明Ai,i-ri≥-1即可.而要使

由泰勒展开式定理和定理1得

令R=O(τ+h2)(1,1,…,1)T,结合(2)、(3)和(13)式,(16)式可写成矩阵形式

所以

进而

4数值实例

考虑如下两边空间分数阶对流-扩散方程

表1给出了当t=0.5时不同时间和不同空间步长下数值解与精确解之间的最大模误差及其误差比率,其中误差比率是由前一行的最大模误差与该行的最大模误差相比而得到.

表 1　t=0.5时的最大模误差和收敛阶

表 2　t=0.5时方程数值解与精确解的比较

5结语

本文考虑了两边空间分数阶对流-扩散方程的数值逼近问题,首先采用Grünwald公式和移位Grünwald-Letnikov公式近似空间分数阶导数,得到一种加权显式有限差分解法;然后利用傅里叶变换和特征值法给出差分格式的稳定性分析,借助于最大模估计方法验证差分格式的收敛性,最后通过数值实例验证了文中方法的精确性、可靠性和实用性.

致谢攀枝花学院校级培育项目(2012PY08)、攀枝花学院校级科研项目(2013YB05和2012YB21)、攀枝花学院院级科研创新项目(Y2013-04)和攀枝花学院教育教学研究与改革青年项目(JJ1376)对本文给予了资助,谨致谢意.

参考文献

[1] PODLUBNY I. Fractional Differential Equations[M]. New York, London:Academic Press,1999.

[2] HILFER R. Applications of Fractional Calculus in Physics[M]. Singapore:Word Scientific,2000.

[3] MORTON K W, MARYERS D F. Numerical Solution of Partial Differential Equation[M]. Cambridge:Cambridge University Press,2005.

[4] LUCHKO Y. Initial-boundary-value problems for the generalized multi-term time-fractional diffusion equation[J]. J Math Anal Appl,2011,374(2):538-548.

[5] 马亮亮,刘冬兵. 二维变系数空间分数阶电报方程数值解[J]. 辽宁工程技术大学学报(自然科学版),2014,33(3):429-432.

[6] 马亮亮,刘冬兵. 一类维空间Riesz分数阶扩散方程的解析解[J]. 合肥工业大学学报(自然科学版),2014,37(4):506-509.

[7] 马亮亮. 时间分数阶扩散方程的数值解法[J]. 数学的实践与认识,2013,43(10):248-253.

[8] 马亮亮. 一种Caputo分数阶反应-扩散方程初边值问题的隐式差分格式[J]. 贵州师范大学学报(自然科学版),2013,31(1):58-61.

[9] 马亮亮,田富鹏. 空间分数阶Edwards-Wilkinson方程的显式差分近似[J]. 沈阳大学学报(自然科学版),2013,25(3):250-252.

[10] 马亮亮,刘冬兵. 一类反常次扩散方程Neumann问题的有限差分格式收敛性分析[J]. 五邑大学学报(自然科学版),2014,28(1):1-4.

[11] 马亮亮,刘冬兵. 变系数分数阶反应-扩散方程的数值解法[J]. 沈阳大学学报(自然科学版),2014,26(1):76-80.

[12] 马亮亮. 时间分数阶扩散方程的隐式差分近似[J]. 贵州师范大学学报(自然科学版),2014,32(2):79-82.

[13] 刘冬兵,马亮亮. 变时间分数阶反应扩散方程的数值分析[J]. 江南大学学报(自然科学版),2014,13(1):109-112.

[14] 马亮亮,刘冬兵. 高维非齐次时间分数阶电报方程的基本解[J]. 四川师范大学学报(自然科学版),2015,38(1):77-83.

[15] LIU F, ZHUANG P, ANH V, et al. Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation[J]. Appl Math Comput,2007,191(1):2-20.

[16] JIANG H, LIU F, TURNER I, et al. Analytical solutions for the multi-term time-space Caputo-Riesz fractional advection-diffusion equations on a finite domain[J]. J Math Anal Appl,2012,389(2):1117-1127.

[17] CARELLA A R, DORAO C A. Least-squares spectral method for the solution of a fractional advection-dispersion equation[J]. J Comput Phys,2013,232(1):33-45.

[18] 马亮亮,刘冬兵. 高维分数阶cable方程隐式差分逼近[J]. 辽宁工程技术大学学报(自然科学版),2014,33(4):544-547.

[19] 马亮亮,田富鹏. 变系数空间分数阶对流-扩散方程的隐式差分近似[J]. 中北大学学报(自然科学版),2014,35(1):11-14.

[20] 马亮亮. 一种时间分数阶对流扩散方程的隐式差分近似[J]. 西北民族大学学报(自然科学版),2013,34(1):7-12.

[21] 马亮亮. 变系数阶空间分数阶对流-扩散方程的有限差分解法[J]. 沈阳大学学报(自然科学版),2013,25(4):341-344.

[22] 马亮亮. 变时间分数阶非定常对流扩散方程的数值分析[J]. 辽东学院学报(自然科学版),2013,20(3):220-223.

[23] 马亮亮,刘冬兵. 一类变时间分数阶含源项非定常奇异摄动对流扩散方程的数值分析[J]. 沈阳大学学报(自然科学版),2013,25(5):424-427.

[24] 苏丽娟,王文洽. 双边空间分数阶对流-扩散方程的一种有限差分解法[J]. 山东大学学报(理学版),2009,44(10):26-29.

[25] MEERSCHAERT M, TADJERAN C. Finite difference approximations for fractional advection-dispersion flow equations[J]. J Comput Appl Math,2004,172(1):65-77.

[26] MEERSCHAET M, TADJERAN C. Finite difference approximations for two-sided space fractional partial differential equations[J]. Appl Num Math,2006,56(1):80-90.

[27] 夏源,吴吉春. 分数阶对流-弥散方程的数值求解[J]. 南京大学学报(自然科学版),2007,43(4):441-446.

[28] LIU F, ANH V, TURNER I. Numerical solution of the space fractional Fokker-Plank equation[J]. J Comput Appl Math,2004,166(1):209-219.

[29] 马维元,刘华. 两边空间-时间分数阶扩散方程的加权有限差分格式[J]. 华东师范大学学报(自然科学版),2012(3):41-48.

[30] 张红玉,崔明荣. 两类分数阶对流-扩散方程的有限差分方法[J]. 山东大学学报(理学版),2012,47(6):40-48.

[31] 汪向艳,朱琳,芮洪兴. 空间分数阶扩散方程的一种加权显式差分方法[J]. 宁夏大学学报(自然科学版),2014,35(1):1-5.

[32] 徐仲,张凯院,陆全,等. 矩阵简明教程[M]. 北京:科学出版社,2001.

2010 MSC：35R11; 39A99

(编辑郑月蓉)

A Weighted Explicit Finite Difference Method for Two-Sided Space Fractional Advection Diffusion Equation

MA Liangliang,LIU Dongbing

(CollegeofMathematicsandComputer,PanzhihuaUniversity,Panzhihua617000,Sichuan)

Abstract：Based on Grünwald formula and the shifted Grünwald-Letnikov formula, a weighted explicit finite difference method is proposed to solve initial boundary value problems of two-sided space fractional advection diffusion equation. Their stability is analyzed by means of Fourier transform and eigenvalue analysis. Using the technique of maximum norm analysis, it is proved that the scheme convergent under the same condition. Illustrative example is included to demonstrate the validity and applicability of the scheme, and a comparison between the exact analytical and the numerical prediction is made to demonstrate the theoretical results.

Key words：fractional advection diffusion equation; space fractional derivative; weighted difference scheme; convergence; stability; finite difference method

doi:10.3969/j.issn.1001-8395.2016.01.013

中图分类号：O241.82

文献标志码：A

文章编号：1001-8395(2016)01-0076-07

作者简介：马亮亮(1986—),男,讲师,主要从事模型优化和微分方程的研究,E-mail:mllpzh@126.com

基金项目：国家自然科学基金(10671132和60673192)、四川省科技厅项目(2013JY0125)和攀枝花市市级应用技术研究与开发资金项目

收稿日期:2014-05-14

(2014CY-G-22)