受限于微分从属函数的有限阶哈达玛乘积的包含性质

都俊杰,　秦　川*,　邹发伟,　李小飞,　何先平,　冯建中

(1. 长江大学 工程技术学院, 湖北 荆州 434020;　2. 长江大学 信息与数学学院, 湖北 荆州 434000)



受限于微分从属函数的有限阶哈达玛乘积的包含性质

都俊杰1,秦川1*,邹发伟1,李小飞1,何先平2,冯建中2

(1. 长江大学 工程技术学院, 湖北 荆州 434020;2. 长江大学 信息与数学学院, 湖北 荆州 434000)

摘要：定义有限阶哈达玛乘积f*φ1*…*φn,其中f,φi∈A,1≤i≤n,并定义一类在单位圆盘内微分从属于正实部函数的解析函数类C(h,φ1,…,φn,λ),S*(h,φ1,…,φn,λ),K(h,φ1,…,φn,λ),R(h,φ1,…,φn,λ),T(h,φ1,…,φn,λ),利用微分从属理论和凸函数理论研究它们的包含性质.

关键词：凸函数; 解析函数; 哈达玛乘积; 微分从属; 包含关系

设A表示单位圆盘U={z∈C:|z|<1}内具有泰勒展开式

(1)

的解析函数族,并用S、S*(γ)、C(γ)分别表示A中的单叶函数类、γ阶星象函数类、γ阶凸函数类[1-2],这里0≤γ<1.f(z)、g(z)在U内解析,称f从属[3]于g,记作fg,若存在U内的Schwarz函数ω(z)(ω(0)=0,|ω(z)|<1),使f(z)=g(ω(z)).特别地,若g在U内单叶,上述从属关系等价于f(0)=g(0),f(U)⊂g(U).设f(z)由(1)式定义,g(z)由(2)式定义

(2)

f(z)与g(z)的哈达玛乘积(或称卷积)定义为:

设h(z)为U内的凸单叶解析函数,且满足h(0)=1,具有正实部,即Reh(z)>0.记所有满足条件p(0)=1,ph(z∈U)的解析函数族为P(h).对于正实部函数类,目前有很多作者对其包含关系进行研究,其中包括一些泛函分析领域的权威学者(详见文献[4-7]).对于h(z)的特殊子类,如,被称为Janowski函数,如取A=1-2α,B=-1,0≤α<1;取A=1,B=-1,成为目前研究热点(详见文献[8]).

对f,φ1,…,φn∈A,(f*φ1*…*φn)(z)≠0,记f1(z)=f(z)*φ1(z)*…*φn(z),且记

(3)

这里0≤λ≤1.文献[9-18]利用卷积和算子函数定义了微分从属函数类并研究函数类的系数性质、包含关系、凸性等.

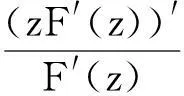
定义 3对f,φ1,…,φn∈A,F由(3)式给出,定义f(z)∈R(h,φ1,…,φn,λ)当且仅当(f*φ1*…*φn)′(z)+λz(f*φ1*…*φn)″(z)h(z).定义f(z)∈T(h,φ1,…,φn,λ)当且仅当zf′(z)∈R(h,φ1,…,φn,λ).

记Sσ(σ≤1)为预星象函数,即f(z)∈Sσ,则

对于预星象函数Sσ,有如下结论：

1)S0=C为凸函数;

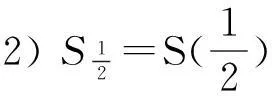
1几个引理

引理 1[19]设f∈Sσ(σ≤1),g为σ阶星象函数,H为U内的解析函数,则

引理 2[20]设h为U上的单叶解析凸函数,且h(0)=1,Re[βh(z)+α]>0(β,α∈C).若p为U上的解析函数且p(0)=h(0),则当

时,有p(z)h(z).

引理 3[21]设β,γ∈C,h(z)为U上的单叶凸函数且h(0)=1,Re[βh(z)+γ]>0,q∈A,q(z)h(z).若p为U内的解析函数且p(0)=1,Req(z)>0,则当

则p(z)h(z).

2主要结论

定理 1C(h,φ1,…,φn,λ)⊂S*(h,φ1,…,φn,λ).

定理 2S*(h,φ1,…,φn,λ),C(h,φ1,…,φn,λ),K(h,φ1,…,φn,λ),R(h,φ1,…,φn,λ),T(h,φ1,…,φn,λ)具有凸卷积不变性.

证明以S*(h,φ1,…,φn,λ)为例证明,其他函数类方法类似.设ψ∈C,f∈S*(h,φ1,…,φn,λ),下证(ψ*f)∈S*(h,φ1,…,φn,λ).经计算

由于f∈S*(h,φ1,…,φn,λ),所以

因此

在引理1中取σ=0,得

由于p为全体P(U)的闭凸包,因此

由S*(h,φ1,…,φn,λ)的定义,知(ψ*f)∈S*(h,φ1,…,φn,λ).

定理 3对任意λ≥0,都有S*(h,φ1,…,φn,λ)⊂S*(h,φ1,…,φn,0).

证明当λ=0时上述包含关系显然成立.现假设λ>0,令f∈S*(h,φ1,…,φn,λ),并记

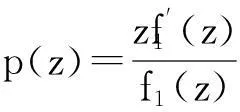
由引理2知,p(z)h(z),即h(z),因此f(z)∈S*(h,φ1,…,φn,0).

定理 4对任意λ≥0,都有K(h,φ1,…,φn,λ)⊂K(h,φ1,…,φn,0).

证明当λ=0时上述包含关系显然成立.当λ>0时,假设f(z)∈K(h,φ1,…,φn,λ),记

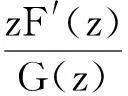
由定理3知,g(z)∈S*(h,φ1,…,φn,λ),则g(z)∈S*(h,φ1,…,φn,0),即p0(z)h(z).经计算

由引理3知,p(z)h(z),即

因此f(z)∈K(h,φ1,…,φn,0).

定理 5T(h,φ1,…,φn,λ)⊂R(h,φ1,…,φn,λ).

证明令f∈T(h,φ1,…,φn,λ),由定义得zf′∈R(h,φ1,…,φn,λ),即

(4)

(4)式左边变形,得

(5)

令p(z)=(f*φ1*…*φn)′+λz(f*φ1*…*φn)″,则(5)式变形为p(z)+zp′(z)h(z),由引理3得,p(z)h(z),即f(z)∈R(h,φ1,…,φn,λ).

定理 6R(h,φ1,…,φn,λ),T(h,φ1,…,φn,λ)为凸集.

证明以函数类R(h,φ1,…,φn,λ)为例证明,对函数类T(h,φ1,…,φn,λ),方法相同.令f1(z),f2(z)∈R(h,φ1,…,φn,λ),即

由于h(U)为凸函数类,因此

即αf1+(1-α)f2∈R(h,φ1,…,φn,λ).

定理 7R(h,φ1,…,φn,λ1)⊂R(h,φ1,…,φn,λ2),0≤λ2<λ1.

为了证明定理7的结论,先证明下面的引理.

引理 4假设λ≥0,D(z)∈S*(h),若N(z)在U内解析,N(0)=D(0)=0,N′(0)=D′(0)=1,h(z)为U内的凸单叶具有正实部即Reh(z)>0的函数,且满足下面的从属关系

定理7的证明若f(z)∈R(h,φ1,…,φn,λ1),则

整理得

由于

这里

由引理4知,(f*φ1*…*φn)′h(z),且h(U)为凸集,因此(1-λ2)(f*φ1*…*φn)′+λ2(z(f*φ1*…*φn)′)′h(z),即f(z)∈R(h,φ1,…,φn,λ2).

同样的方法,可以得到以下定理8～10.

定理 8对任意0≤λ2≤λ1,都有T(h,φ1,…,φn,λ1)⊂T(h,φ1,…,φn,λ2).

定理 9对任意λ≥1,都有T(h,φ1,…,φn,λ)⊂T(h,φ1,…,φn,1).

定理 10对λ≥0,f,φ1,…,φn∈A,设

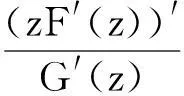
致谢长江大学科研发展基金(2013CJY01)、长江大学应用数学研究所开放基金(KF1508)和长江大学工程技术学院科技创新基金(15J0802)对本文给予了资助,谨致谢意.

参考文献

[1] 杨定恭. 关于具有负系数的p叶星象函数的注记[J]. 纯粹数学与应用数学,1993,9(1):119-122.

[2] SILVERMAN H. Univalent functions with negative coefficients[J]. Proc Am Math Soc,1975,51:109-116.

[3] POMMERENKE C. Univalent Functions[M]. Gottengen:Vanderhoeck and Ruprecht,1975.

[4] YANG D G, LIU J L. A class of meromorphically multivalent functions defined by means of a linear operator[J]. Appl Math Comput,2008,204:862-871.

[5] HE P, ZHANG D F. Certain subclasses of meromorphically multivalent functions associated with the linear operator[J]. Appl Math Lett,2011,24:1817-1822.

[6] XU Q H, SRIVASTAVA H M, LI Z. A certain subclass of analytic and close-to-convex functions[J]. Appl Math Lett,2011,24:396-401.

[7] ROSIHAN M, LEE S K, RAVICHANDRAN V, et al. Coefficient estimates for bi-univalent Ma-Minda starlike and convex functions[J]. Appl Math Lett,2012,25:344-351.

[8] GOODMAN A W. Univalent Functions[M]. New Jersey:Polygonal Publishing House,1983.

[9] SRIVASTAVA H M, YANG D G, XU N E. Some subclasses of meromorphically multivalent functions associated with a linear operator[J]. Appl Math Comput,2008,195(1):11-23.

[10] AOUF M K. Subordination properties for a certain class of analytic functions defined by the Salagean operator[J]. Appl Math Lett,2009,22(10):1581-1585.

[11] 李小飞,严证. 某类积分解析算子函数的性质[J]. 湖南师范大学学报(自然科学版),2014,36(4):11-15.

[12] BRANNAN D A, TAHA T S. On some classes of bi-univalent functions[J]. Mathematical Analysis and Its Applications,1985,2:18-21.

[13] 李小飞,秦川. 一类利用从属关系定义的双单叶函数类[J]. 四川师范大学学报(自然科学版),2014,37(4):511-414.

[14] XU Q H, GUI Y C, SRIVASTAVA H M. Coefficient estimates for a certain subclass of analytic and bi-univalent functions[J]. Appl Math Lett,2012,25(6):990-994.

[15] 熊良鹏,李小飞,刘晓丽. 受限于从属族的bi-单叶函数的系数边界[J]. 河南师范大学学报(自然科学版),2013,41(3):15-18.

[16] DZIOK J. Classes of meromorphic functions associated with conic region[J]. Acta Mathematica Scientia,2012,B32:765-774.

[17] FAISAL I, DARUS M. A study of a special family of analytic functions at infinity[J]. Appl Math Lett,2012,25:765-774.

[18] SIREGAR S. The starlikeness of analytic functions of Koebe type[J]. Math Comput Model,2011,54:2928-2938.

[19] RUSCHEWEYH S. Convolutions in Geometric Function Theory[M]. Montreal:Les Presse de Universite de Montreal,1982.

[20] MILLER S S, MOCANU P T. Differential Subordination Theory and Applications[M]. New York, Basel:Marcel Dekker Inc,2000.

[21] EENIGENBURG P, MOCANU P T, MILLER S S, et al. On a Briot-Bouquet differential subordination in general inequalities[J]. Internationale Schriftenreihe Numerischen Mathematik,1984,64:329-348.

2010MSC：30C45

(编辑周俊)

Inclusion Properties of Hadamard Product of Finitely Order Defined by Differential Subordination

DU Junjie1,QIN Chuan1,ZOU Fawei1,LI Xiaofei1,HE Xianping2,FENG Jianzhong2

(1.EngineeringandTechnologyCollegeofYangtzeUniversity,Jingzhou434020,Hubei;2.SchoolofInformationandMathematics,YangtzeUniversity,Jingzhou434000,Hubei)

Abstract：The Hadamard product of finitely order is defined with f*φ1*…*φn,f,φi∈A(1≤i≤n). The classes of analytic functions C(h,φ1,…,φn,λ),S*(h,φ1,…,φn,λ) and K(h,φ1,…,φn,λ),R(h,φ1,…,φn,λ),T(h,φ1,…,φn,λ) are defined in unit disc by differential subordination. Inclusion properties are obtained by using differential subordination and convolution.

Key words：convex function; analytic function; Hadamard product; differential subordination; inclusion properties

doi:10.3969/j.issn.1001-8395.2016.01.012

中图分类号：O174.51

文献标志码：A

文章编号：1001-8395(2016)01-0071-05

*通信作者简介：秦川(1985—),女,讲师,主要从事复分析的研究,E-mail:dujunjie0420@163.com

基金项目：湖北省自然科学基金(2013CFAO053)和湖北省教育厅科研项目(B2013281)

收稿日期:2015-04-28