不同斜交角度简支T形梁桥基频计算与试验
2016-05-06张等
张 等
(育才-布朗交通咨询监理有限公司, 湖南 长沙 410076)
不同斜交角度简支T形梁桥基频计算与试验
张等
(育才-布朗交通咨询监理有限公司, 湖南 长沙410076)
摘要:以某装配式后张法预应力混凝土简支斜交T形梁桥为工程实例,采用MIDAS Civil软件建立空间梁格模型,对不同斜交角简支T形梁桥的动力特性进行分析,提出斜交T形梁桥的基频随斜交角度变化的计算修正公式。分析表明:当斜交角小于20°时,竖向频率可以按照正交桥计算,当斜交角度为20°~55°时,频率与正交桥差异相差很大,计算冲击系数明显增大,直接影响桥梁结构内力设计。因此,在斜桥设计时必须引起足够重视。通过现场动荷载试验测试得出基频与拟合公式计算结果十分接近,说明该拟合公式能够较准确计算斜交T形梁桥的竖向基频值。
关键词:T形梁桥; 斜交角; 基频; MIDAS Civil软件; 动荷载试验
1背景
斜交桥与正桥不同,其梁轴线的方向与支座连线不平行,所形成的夹角称为斜交角。随着我国大规模的桥梁建设,斜交桥比例越来越大,据统计,目前在高速公路上的斜桥的数量可达到整条线路桥梁总数的 40%~50%,但是斜交桥动力特性仍处于待研究阶段,在车辆、风、地震等动力荷载作用下,斜交桥破坏可能性要大于正交桥。林玉良、李威等对某简支斜箱梁桥的静动力特性进行了分析研究,并将其与等宽同跨径的正桥的力学特性进行了对比,得出斜箱梁桥特有的应力分布规律、动力特性以及空间作用效应规律[1]。何旭辉等对PC斜交箱梁的振动特性进行模型试验研究,得到了PC斜交箱梁桥的振型与斜交角度之间的关系[2]。夏樟华、宗周红等以三跨斜交T梁桥为背景,分析了不同斜交角时动力特性的差异,探讨了此类斜交桥的动力特性得出了竖向和扭转频率随斜交角的增大而增大[3,4]。但并没给出具体的简支斜交T形梁桥基频的计算公式,给设计人员带来一定困惑。
本文以某装配式后张法预应力混凝土简支T形梁桥为背景,应用Midas Civil软件建立空间梁格模型,计算不同斜交角度下的频率值,得出频率随斜交角度的变化规律,并根据计算结果对规范中给出的基频公式进行修正,提出了适应于简支斜交T形梁桥的基频计算公式,计算结果与现场试验结果十分接近。
2工程实例与有限元模型
2.1工程概况
某装配式后张法预应力混凝土简支T形梁桥,横桥向布置5片T梁,标准跨径为30 m,计算跨径为28.92 m,桥面宽11 m+2×0.5 m防撞墙,斜交角度30°,布设5道横隔板,其中3道中横隔板,2道端横隔板,横隔板均为斜置,T形梁及横隔板均采用C50混凝土,桥面铺装为10 cm厚现浇混凝土+10 cm沥青混凝土,汽车荷载为公路Ⅰ级,结构重要性系数取1.1,支座采用圆形板式橡胶支座,弹簧刚度系数SDx=SDy=2 438 kN/m,SDz=2 550 000 kN/m,SRx=SRy=SRz=0,几何尺寸见图1~图4。
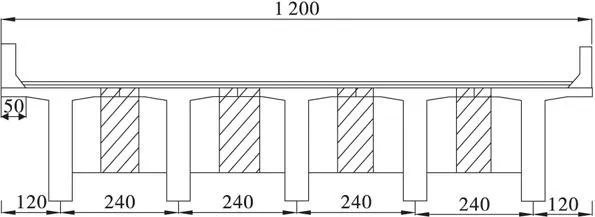
图1 横截面布置(单位: cm)
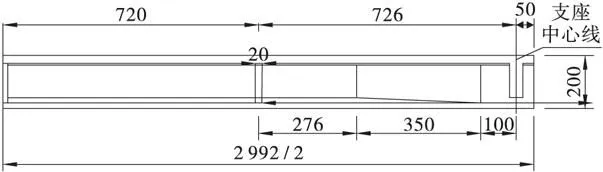
图2 半立面(单位: cm)
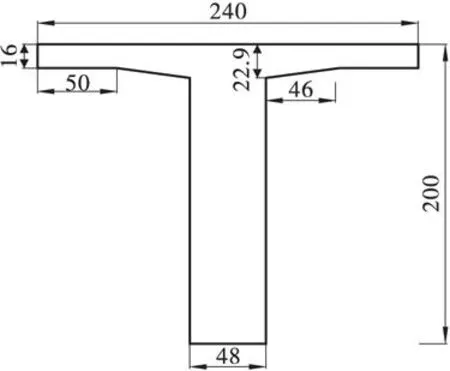
图3 支点截面尺寸(单位: cm)
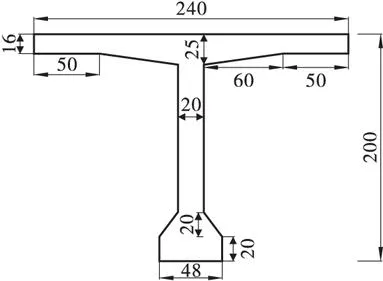
图4 跨中截面尺寸(单位: cm)
2.2梁格模型
空间梁格理论是把分散在板上每一区段内的弯曲和抗扭刚度集中在最邻近的等效梁格内,板的纵向刚度集中在纵向梁格内,横向刚度集中在横向梁格内。理论上要求当原型实际结构和对应的等效梁格承受相同荷载时,两者的挠曲恒等,任一梁格内的弯矩、剪力和扭矩也与梁格所代表实际结构的内力相等。
由于斜交角的存在,对平面杆系单元并不实用,对实体单元建模太繁琐,结果处理困难,采用梁格模型很好解决这一问题;采用Midas Civil软件建立梁格模型,全桥共设5根纵梁,每一纵梁代表一片T梁。横向联系由两部分构成,一部分为实际横梁横隔板,另一部分称为虚拟横梁,设在横隔板之间用来联系纵梁。虚拟横梁混凝土容重取零,高度取T梁翼缘厚度16 cm。虚拟横梁布置形式通常有两种方法:一是平行于横隔板方向,其适用于斜交角度小于15°,见图5;二是垂直于主梁方向,其适用于斜交角大于15°,见图6。
支座点的建立,可由梁上翼缘对应节点向下复制支座节点,距离为梁高2 m,选择弹性连接的“刚性”进行梁与支座的连接,但是由于桥梁斜交角轴线与支撑边线法线方向夹角为30°,梁底支座也是斜置,通过定义“节点局部坐标轴”模拟支座的方向。
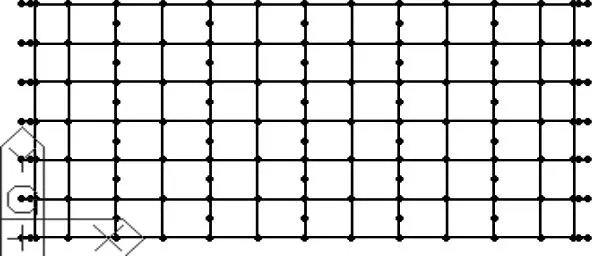
图5 平行支撑线布置横向梁格模型

图6 垂直于主梁布置横向梁格模型
3结果分析
本文针对装配式后张法预应力混凝土简支T形梁桥,根据斜交角度0°~55°(间隔5°)变化分别建立空间梁格模型;为了得到结构的竖向基频,从而计算汽车的冲击系数;空间梁格模型中需要将结构自重转换为质量,特征值分析控制采用Lanczos法。计算前3阶(高阶振型对桥梁影响较小)自振频率f1,f2,f3和周期T1,T2,T3,计算结果见表1,振型见图7~图9。
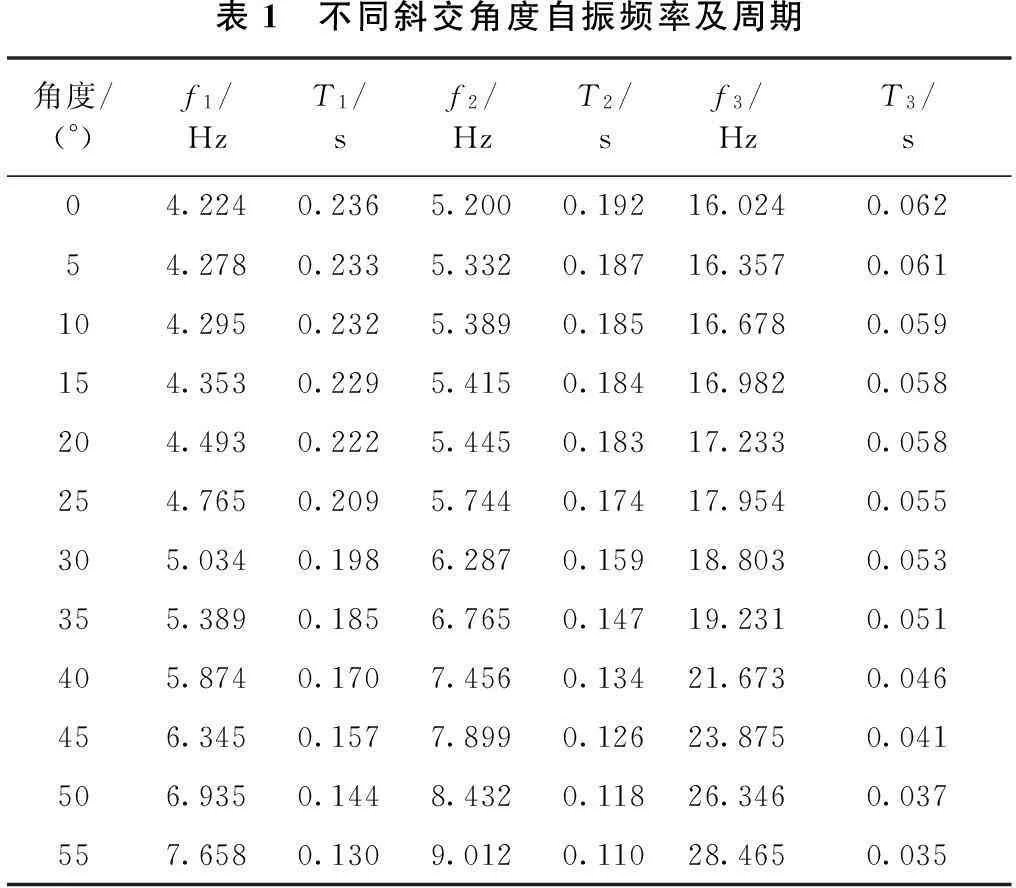
表1 不同斜交角度自振频率及周期角度/(°)f1/HzT1/sf2/HzT2/sf3/HzT3/s04.2240.2365.2000.19216.0240.06254.2780.2335.3320.18716.3570.061104.2950.2325.3890.18516.6780.059154.3530.2295.4150.18416.9820.058204.4930.2225.4450.18317.2330.058254.7650.2095.7440.17417.9540.055305.0340.1986.2870.15918.8030.053355.3890.1856.7650.14719.2310.051405.8740.1707.4560.13421.6730.046456.3450.1577.8990.12623.8750.041506.9350.1448.4320.11826.3460.037557.6580.1309.0120.11028.4650.035
从表1可以看出,对装配式后张法预应力混凝土简支T形梁桥,一、二、三阶频率均随着斜交角度的增加而增大,其中二、三阶频率随斜交角度变化斜率比一阶频率大的多。然而为了得到简支梁桥冲击系数,采用的是一阶自振频率;当斜交角度为20°~55°,一阶频率相比正交时分别增大了6.3%、12.8%、19.2%、27.6%、39%、50.2%、64.2%、81.2%,计算桥梁汽车荷载冲击系数相比正交桥分别增大4.6%,8.7%,12.9%,17.9%,24.2%,30.2%,36.4%,43.9%。可以看出,随着冲击系数的增大,直接影响桥梁结构内力设计取值。

图7 一阶振型
图8 二阶振型

图9 三阶振型
采用最小二乘法对表1数据进行拟合,从图10得知,当斜交角小于20°时,曲线接近水平,频率可以按照正交桥计算。当斜交角度20°~55°时,频率与正交桥差异相差很大,导致冲击系数的增大,直接影响到桥梁结构内力设计取值,对于斜桥设计时,必须考虑斜角度对桥梁结构的影响。
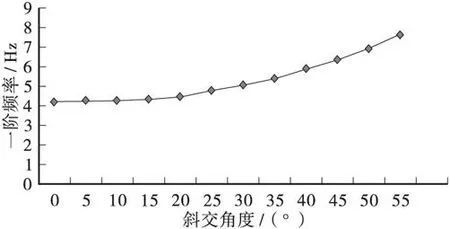
图10 一阶频率拟合曲线
则考虑到斜交角后,一阶频率(简支T梁)修正计算公式为:
式中:ε=1.040 2θ2-0.191 6θ+1(0≤θ≤40°);
ε=1.782 2θ-0.102 2(θ>40°)。
4现场动载试验
斗光桥位于娄底市中心城区内环线扩建工程(碧溪路-早元西街),在建高丰路右侧;整体布置为2×35 m预应力混凝土简支T梁(见图11),其斜交角度为28°,进行现场动载试验。

图11 工程概貌
4.1基频测定
跳车试验是在预定激振位置,汽车后轮越过一根高15 cm的有坡面的横木,车轮落下后立即停车,激发桥梁垂直振动,测量桥梁结构的振动响应,并通过采用高灵敏度的拾振器和放大器测量结构在激励下的振动,测量桥梁结构的振动响应,最后进行谱分析,求出结构自振特性。在试验跨跨中进行跳车(见图12),跳车试验时域及频域曲线见图13。

图12 跳车试验
经数据处理分析可以得出该桥一阶自振频率为5.0 Hz,根据拟合此类桥梁基频计算公式计算得出f=4.9 Hz。因此,拟合计算公式能够较准确计算桥梁一阶自振频率理论值。
4.2冲击系数测定
采用自重为30 t汽车,分别以20、 30 km/h的速度匀速驶过桥面,测量试验跨跨中截面的动应变响应,通过对动应变时间历程信号的分析处理,得到测试部位的冲击系数,冲击系数波形分析图见图14、图15。冲击系数分析结果见表2。
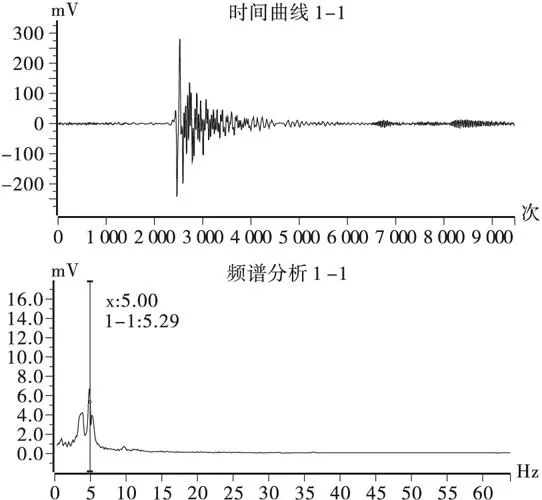
图13 跳车试验时域及频域曲线

图14 实测20 km/h冲击系数波形分析图

图15 实测30 km/h冲击系数波形分析图
由表2可得,现场测试的冲击系数反推出的基频值与拟合公式计算得出的结果4.9 Hz十分接近,实测值要大于理论值,说明桥梁实际刚度大于设计刚度。因此,该拟合公式能够较准确计算斜交T形梁桥的竖向基频值。

表2 冲击系数μ实测结果速度/(km·h-1)实测冲击系数μ《桥规》4.3.2公式计算基频[5]/Hz201.2765.2301.2695.0
5结论
1) 当斜交角小于20°时,竖向频率可以按照正交桥计算;当斜交角度为20°~55°时,频率与正交桥差异相差很大,计算冲击系数明显增大,设计等级应提高。
2) 通过大量空间有限元数值模拟,提出了斜交T形梁桥的竖向基频计算修正公式,为斜交T形梁桥的设计提供了理论计算依据。
3) 通过现场动荷载试验测试得出实测基频与拟合公式计算结果十分接近,说明该拟合公式能够较准确计算斜交T形梁桥的竖向基频值。
参考文献:
[1] 林玉良,李威.斜梁桥力学特性分析[J].北方交通,2006(9):54-58.
[2] 何旭辉,盛兴旺,陈政清.高速铁路PC斜交箱梁桥振动特性模型试验研究[J].铁道学报,2002(5):11-17.
[3] 夏樟华,宗周红.三跨斜交T梁动力特性分析[J].振动与冲击,2007(4):44-50.
[4] 郭向荣,陈淮.预应力混凝土T形梁桥动力特性分析模型[J].计算力学学报,2000(2):1-8.
[5] JTG D60-2004,公路桥涵设计通用规范[S].
中图分类号:U 448.21+2
文献标识码:A
文章编号:1008-844X(2016)01-0074-04
