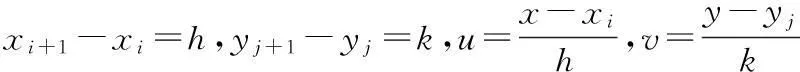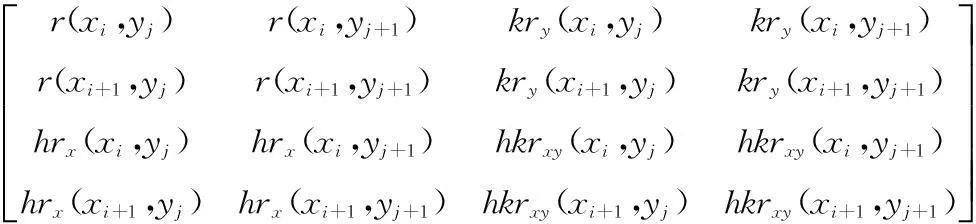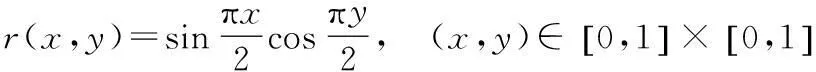自动满足C2连续的带参数五次Hermite插值样条

李军成, 谢　炜

(1. 湖南人文科技学院 数学系, 湖南 娄底 417000; 2. 桂林理工大学 理学院, 广西 桂林 541004)



自动满足C2连续的带参数五次Hermite插值样条

李军成1, 谢炜2

(1. 湖南人文科技学院 数学系, 湖南 娄底 417000; 2. 桂林理工大学 理学院, 广西 桂林 541004)

摘要：为了克服已有的带形状参数的三次或四次Hermite型插值样条不能自动满足C2连续这一不足,提出了一类新的五次Hermite插值样条.该样条除了具有带形状参数Hermite型插值样条的特性外,在插值条件保持不变的情形下可自动满足C2连续且其形状还可通过所带的形状参数进行调控.进一步,给出了一种确定形状参数最优取值的方法,该法可使得五次Hermite插值样条曲线具有最优插值效果.

关键词：Hermite插值;五次Hermite插值样条;C2连续;形状调控

LI Juncheng1, XIE Wei2

(1.DepartmentofMathematics,HunanUniversityofHumanities,ScienceandTechnology,Loudi417000,HunanProvince,China; 2.CollegeofScience,GuilinUniversityofTechnology,Guilin541004,GuangxiZhuangAutonomousRegion,China)

在计算机辅助设计、几何造型、计算机图形学等实际工程技术问题中,人们往往需要对曲线曲面的形状进行灵活调控.因此,构造带形状参数的曲线曲面逐渐成为几何造型与计算中的一个研究热点.例如,带形状参数的Bézier曲线曲面[1-4]以及B样条曲线曲面[5-8]等.这些带有形状参数的曲线曲面不但保留了原曲线曲面的性质,而且其形状可通过所带的形状参数进行灵活调控.由于三次Hermite插值样条是工程中常见的一种插值模型,但当插值条件固定时,传统三次Hermite插值样条的形状却无法调控,因此也有一些学者构造了带形状参数的Hermite型插值样条.例如,带形状参数的有理三次三角Hermite插值样条[9]、有理三次Hermite插值样条[10]、四次Hermite插值样条[11]、三次三角Hermite插值样条[12]等.这些带形状参数的Hermite型插值样条除了具有传统三次Hermite插值样条的插值性与C1连续性外,在插值条件保持不变的情况下可利用形状参数灵活调控其形状.

注意到,为了使插值样条满足C2连续,上述带形状参数的Hermite型插值样条[9-12]均是通过对形状参数施加C2连续性约束条件后,再通过迭代计算所有形状参数值.这种方法不但增大了计算量,而 且通过迭代计算得到的形状参数值均为近似值,当样条的分段较多时,随着误差的累积，靠后相邻的样条段的C2连续性就无法保证.为此,本文构造了一种带形状参数的五次Hermite插值样条,该样条除了具有带形状参数的Hermite型插值样条的特性外,在插值条件保持不变时还可自动满足C2连续,同时可利用形状参数对其形状进行调控.为了方便应用,本文给出了一种确定形状参数最优取值的方法,以使得五次Hermite插值样条具有最优插值效果.

1基函数的定义及性质

定义1对∀λ,μ∈R,0≤t≤1,称

(1)

为带形状参数λ与μ的五次Hermite基函数.

定理1五次Hermite基函数具有如下性质：

(i)五次Hermite基函数在端点处满足：

(2)

(3)

(4)

(ii)固定t∈[0,1],αi(t)(i=0,1)关于参数λ单调递增,βi(t)(i=0,1)关于参数μ单调递增.

证明(i)将式(1)改写成矩阵形式：

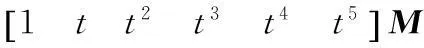
(5)

式中

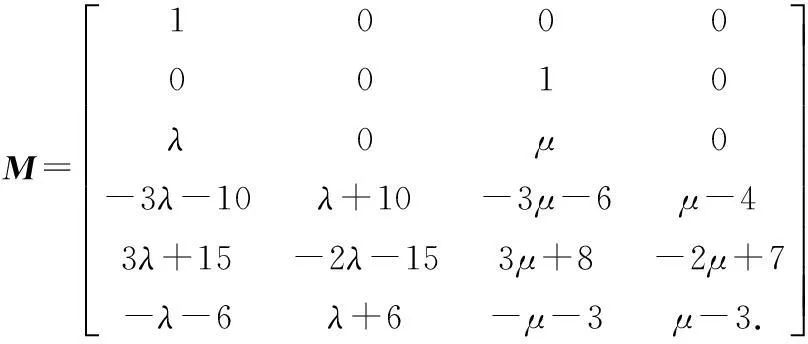
对式(5)两端分别求关于t的一阶与二阶导数，有

将t=0与t=1分别代入式(5)并经简单计算可知式(2)成立.同理可知式(3)与(4)成立.

(ii)固定t∈[0,1],经简单计算可得

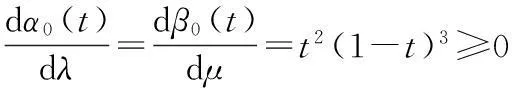
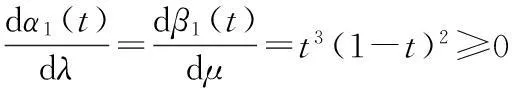
故αi(t)(i=0,1)关于参数λ单调递增,βi(t)(i=0,1)关于参数μ单调递增.

注1定理1表明,五次Hermite基函数不仅与传统三次Hermite基函数在端点处具有相同的性质,而且由于带形状参数λ与μ,故当形状参数取不同值时可得到不同形状的五次Hermite基函数图形,见图1.

图1　形状参数取不同值时的五次Hermite基函数 Fig.1　Quintic Hermite basis functions with different shape parameters

其中，短虚线对应的形状参数为λ=-1与β=2,实线对应的形状参数为λ=β=0,长虚线对应的形状参数为λ=2与β=-1.

2样条曲线

2.1样条曲线的定义与特性

由于在实际工程技术问题中经常会遇到节点等距分布的情形,同时也为了使得所构造的五次Hermite插值样条曲线具有更好的特性,下面仅讨论节点等距分布情形下的Hermite型插值样条曲线.

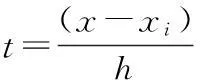
si(x)=α0(t)yi+α1(t)yi+1+β0(t)hdi+β1(t)hdi+1

(6)

为区间[a,b]上带形状参数λ与μ的五次Hermite插值样条曲线,其中αj(t)与βj(t)(j=0,1)为式(1)定义的五次Hermite基函数.

定理2五次Hermite插值样条插值于给定的数据且满足C2连续,即有

(7)

其中，i=0,1,2,…,n-1；

(8)

其中，i=0,1,2,…,n-2.

证明由式(2)、(3)与(6)，有

(9)

(10)

由式(9)与(10)可得式(7)成立,且有

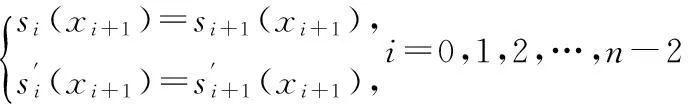
(11)

又由式(4)与(7),有

(12)

由式(12)可知

s″i(xi+1)=s″i+1(xi+1),i=0,1,2,…,n-2.

(13)

由式(12)与(13)可得式(8)成立.

注2定理2表明,五次Hermite插值样条曲线不仅继承了传统三次Hermite插值样条曲线的插值性与连续性,而且还具有如下特性:

(1)当数据保持不变时,传统三次Hermite插值样条曲线的形状无法灵活调控,而带有形状参数λ与μ后,便可通过这2个形状参数对五次Hermite插值样条曲线的形状进行调控.

(2)传统三次Hermite插值样条仅满足C1连续,而五次Hermite插值样条不仅可自动满足C2连续,而且还可通过修改形状参数λ与μ的值对其形状进行调控.

例1给定数据点如表1所示.

表1　给定的插值条件

传统三次Hermite插值样条曲线及形状参数λ与μ取不同值时五次Hermite插值样条曲线如图2所示.

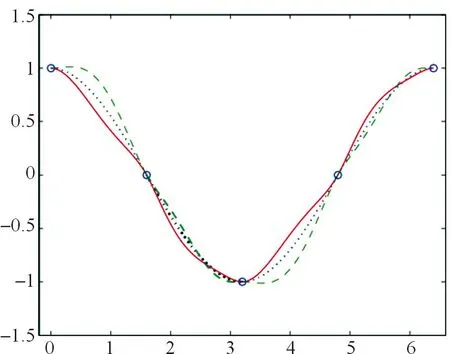
图2　形状参数取不同值时的五次Hermite插值样条曲线Fig.2　Quintic Hermite interpolating spline curves with different shape parameters

其中短虚线为传统三次Hermite插值样条曲线,实线与长虚线分别为形状参数取(λ,μ)=(-3,2)与(λ,μ)=(1,-2)时的五次Hermite插值样条曲线.

注3虽然文献[9-12]也构造了几类与传统三次Hermite插值样条曲线具有相同性质的Hermite型插值样条曲线,而且这些曲线的形状均可通过所带的形状参数进行调控.但是,无论节点是否为等距分布,为了使所构造的样条曲线满足C2连续,这些样条曲线均需通过对形状参数施加C2连续性约束条件后再迭代计算所有的形状参数值.这样,一方面会增加计算量,另一方面由于形状参数的值均由迭代方式计算所得,因此当给定的数据较多时,靠后相邻曲线段的C2连续性会因累积误差的增大而无法保证.当节点为等距分布时,本文所构造的五次Hermite插值样条即可自动满足C2连续,且其形状还可通过形状参数λ与μ进行调控,从而使其在实际应用中更具优势.

2.2形状参数的最优取值

由前文可知,当数据(xi,yi,di)(i=0,1,2,…,n)给定时,五次Hermite插值样条曲线si(x)(i=0,1,…,n-1)的形状由形状参数λ与μ决定.在实际应用中,若形状参数λ与μ的值选取不当时,会导致五次Hermite插值样条曲线的插值效果较差.

例2给定函数

y=r(x)=3+2cosx(0≤x≤5π),

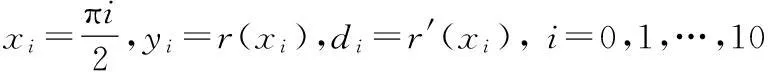
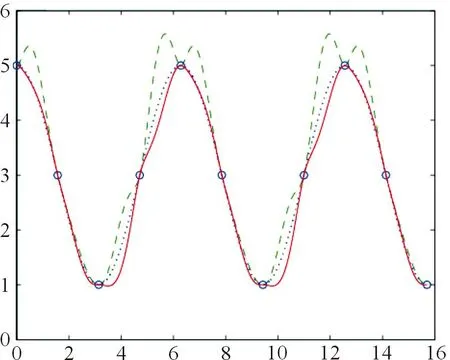
图3　形状参数对五次Hermite插值样条曲线的影响Fig.3　Effect of the shape parameters on quintic Hermite interpolating spline curves

其中实线对应的参数为(α,β)=(-1,-2),长虚线对应的参数为(α,β)=(3,2),短虚线为函数y=f(x)的曲线图.

由图3可知,形状参数(α,β)=(-1,-2)时比(α,β)=(3,2)时的五次Hermite插值样条曲线具有更为满意的插值效果.

当给定函数y=r(x)(a≤x≤b)时,设xi=a+hi(常数h>0)为区间[a,b]的一个等距划分,yi=r(xi),di=r′(xi)(i=0,1,…,n),如何选取合适的形状参数λ与μ,使得插值于函数y=f(x)的五次Hermite插值样条具有最佳插值效果？为解决这一问题，下面给出一种确定五次Hermite插值样条曲线最优形状参数取值的方法.

插值于函数y=r(x)的五次Hermite插值样条曲线的整体插值误差可表示为

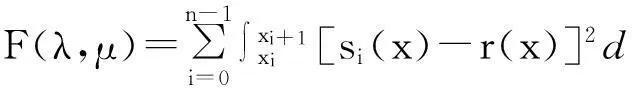
(14)

记

M0(t)=t2-3t3+3t4-t5,

N0(t)=1-10t3+15t4-6t5,

M1(t)=t3-2t4+t5,

N1(t)=10t3-15t4+6t5,

N2(t)=t-6t3+8t4-3t5,

N3(t)=-4t3+7t4-3t5.

则式(6)可改写为

si(x)=L0(x)λ+L1(x)μ+L2(x)，

(15)

其中，

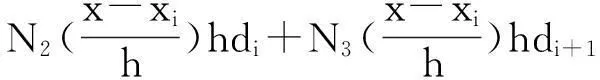
由式(15),式(14)可改写为

C0λ2+C1μ2+2C2λμ+2C3λ+2C4μ+C5.

(16)

其中,

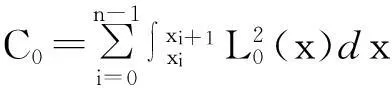
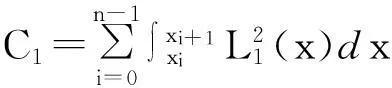
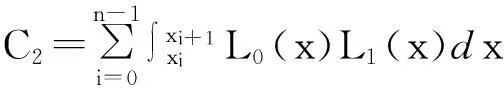
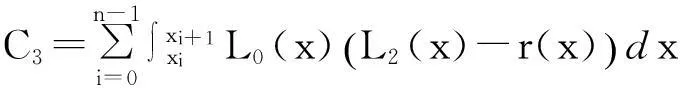
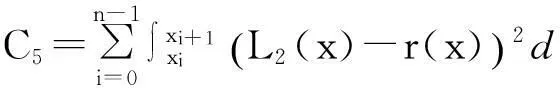
要使得式(16)取最小值,则必有

(17)

由式(16)可知,式(17)可改写为

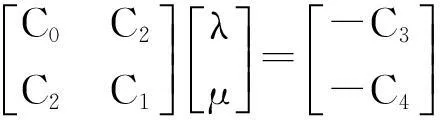
(18)

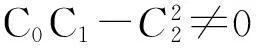
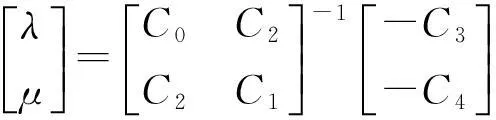
(19)

由式(19)计算形状参数λ与μ的最优取值后,便可获得插值于函数y=r(x)的最优五次Hermite插值样条曲线.

例3对于例2中给定的插值条件,由式(19)计算可得五次Hermite插值样条曲线形状参数的最优取值为λ=-0.137 2与μ=-0.480 4.函数y=f(x)的曲线图(短虚线)与五次Hermite插值样条曲线(实线)如图4所示.

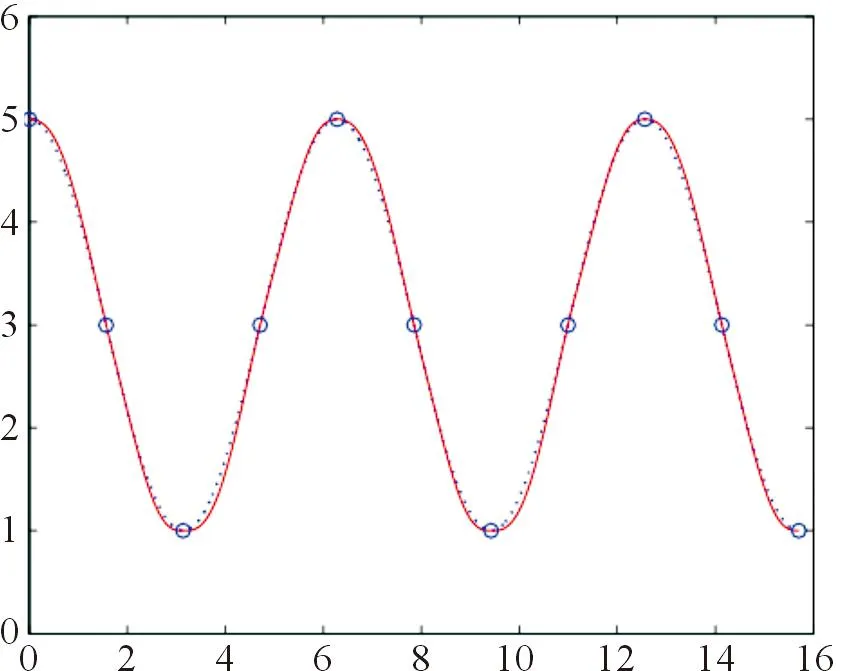
图4　最优五次Hermite插值样条曲线Fig. 4　The optimal quintic interpolating spline curve

由图4可知,当形状参数取最优值时,五次Hermite插值样条曲线与原曲线几乎重合,即能获得满意的插值效果.

3样条曲面

利用张量积,可类似定义带形状参数的五次Hermite插值样条曲面.

定义3设r(x,y)为定义在区域[a,b]×[c,d]的二元函数,且存在二阶偏导数.

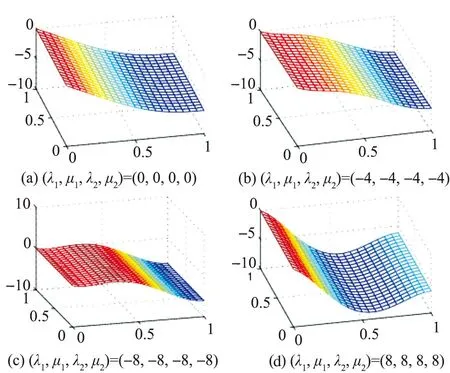
Δ:a=x0

c=y0

是区域[a,b]×[c,d]的一个等距划分网格,记

对于(x,y)∈[xi,xi+1]×[yj,yj+1],i=0,1,2,…,m-1;j=0,1,2,…,n-1,

称

sij(x,y)=

为区域[a,b]×[c,d]上插值于函数r(x,y)的带形状参数的五次Hermite插值样条曲面,其中，

M=

αi(t)与βi(t)，t=u,v;i=0,1为参照式(1)定义的五次Hermite基函数,且u向与v向的形状参数分别为λj与μj(j=1,2).

易知,五次Hermite插值样条曲面除了具有插值性外,在插值条件保持不变时,不仅自动满足C2连续,而且其形状还可通过形状参数λj与μj(j=1,2)进行调控.当形状参数取最优值时,可利用五次Hermite插值样条曲面获得满意的插值效果.

例4给定函数

取xi=i,yj=j.当形状参数λj与μj(j=1,2)取不同值时，五次Hermite插值样条曲面片如图5所示.

图5　形状参数取不同值时的五次Hermite插值样条曲面片Fig.5　Quintic Hermite interpolating spline patches with different shape parameters

由图5可知,当插值条件保持不变时,通过调整形状参数λj与μj,j=1,2，实现了对五次Hermite插值样条曲面片形状的调控.

4结语

提出了一类带形状参数的Hermite型插值样条,该样条不仅继承了传统三次Hermite插值样条的性质,而且可自动满足C2连续.固定插值条件时,C2连续的五次Hermite插值样条曲线可利用所带的形状参数对其形状进行调控.为了方便实际应用,本文还给出了一种确定五次Hermite插值样条曲线最优形状参数取值的方法,实例结果表明,利用该方法确定的形状参数可使得五次Hermite插值样条曲线具有较好的插值效果.最后,将样条推广到曲面形式,给出了带形状参数的五次Hermite插值样条曲面的定义及性质.由于本文提出的五次Hermite插值样条是多项式模型,方程结构较为简洁,为插值曲线曲面的构造提供了新选择.

参考文献(References)：

[1]YAN Lanlan, LIANG Qiongfeng. An extension of the Bézier model[J]. Applied Mathematics and Computation,2011,218(6):2863-2879.

[2]BASHIR U, ABBSA M, ALI J M. TheG2andC2rational quadratic trigonometric Bézier curve with two shape parameters with applications[J]. Applied Mathematics and Computation,2013,219(20):10183-10197.

[3]LI Juncheng. A class of cubic trigonometric Bézier curve with a shape parameter[J]. Journal of Information and Computational Science,2013,10(10):3071-3078.

[4]徐迎博,喻德生.带形状参数的二次三角Bézier曲线形状分析[J].浙江大学学报:理学版,2013,40(1):35-41.

XU Yingbo, YU Desheng. Shape analysis of quadratic trigonometric polynomial Bézier curves with a shape parameter[J]. Journal of Zhejiang University: Science Edition,2013,40(1):35-41.

[5]LIU Xumin, XU Weixiang, GUAN Yong, et al. Hyperbolic polynomial uniform B-spline curves and surfaces with shape parameter[J]. Graphical Models,2010,72(1):1-6.

[6]CAO Juan, WANG Guozhao. Non-uniform B-spline curves with multiple shape parameters[J]. Journal of Zhejiang University: Science C,2011,12(10):800-808.

[7]左传桂,汪国昭.多形状参数的四阶均匀B样条曲线设计[J].浙江大学学报:理学版,2007,34(4):401-404.

ZUO Chuangui, WANG Guozhao. Curve design of multi-parameter uniform B-spline blending function of order four[J]. Journal of Zhejiang University: Science Edition,2007,34(4):401-404.

[8]左传桂,汪国昭.具有2个独立形状参数的四阶均匀B样条[J].浙江大学学报:理学版,2007,34(6):622-627.

ZUO Chuangui, WANG Guozhao. Uniform B-spline of order four with independent shape parameters[J]. Journal of Zhejiang University: Science Edition,2007,34(6):622-627.

[9]谢进,檀结庆,刘植,等.一类带参数的有理三次三角Hermite插值样条[J].计算数学,2011,33(2):125-132.

XIE Jin, TAN Jieqing, LIU Zhi, et al. A class of rational cubic trigonometric Hermite interpolating splines with parameters[J]. Mathematica Numerica Sinica,2011,33(2):125-132.

[10]谢进,檀结庆,李声锋.有理三次Hermite插值样条及其逼近形状[J].工程数学学报,2011,28(3):385-392.

XIE Jin, TAN Jieqing, LI Shengfeng. Rational cubic Hermite interpolating spline and its approximation properties[J]. Chinese Journal of Engineering Mathematics,2011,28(3):385-392.

[11]李军成,刘纯英,杨炼.带参数的四次Hermite插值样条[J].计算机应用,2012,32(7):1868-1870.

LI Juncheng, LIU Chunying, YANG Lian. Quartic Hermite interpolating splines with parameters[J]. Journal of Computer Applications,2012,32(7):1868-1870.

[12]李军成,钟月娥,谢淳.带形状参数的三次三角Hermite插值样条曲线[J].计算机工程与应用,2014,50(17):182-185.

LI Juncheng, ZHONG Yuee, XIE Chun. Cubic trigonometric Hermite interpolating splines curves with shape parameters[J]. Computer Engineering and Applications,2014,50(17): 182-185.

The automatic C2continuous quintic Hermite interpolating spline with parameters. Journal of Zhejiang University(Science Edition), 2016,43(2):175-180

Abstract:In order to solve the problem that the cubic or quartic Hermite-type interpolating splines with shape parameters can not automatically satisfy C2 continuity, a new class of quintic Hermite interpolating spline with shape parameters is presented. The proposed spline not only has the same characteristics as the Hermite-type interpolating spline with shape parameters, but also automatically satisfies C2 continuity and can be controlled by the shape parameters when the interpolation conditions remain unchanged. Furthermore, a method for determining the optimal value of the shape parameters is given, which can make the quintic Hermite interpolating spline curve with the optimal interpolation effects.

Key Words:Hermite interpolation; quintic Hermite interpolating spline; C2 continuity; shape adjustment

中图分类号：O 241.5；TP 391

文献标志码：A

文章编号：1008-9497(2016)02-175-06

DOI:10.3785/j.issn.1008-9497.2016.02.009

作者简介：李军成(1982-),ORCID:http:/orcid.org/0000-0002-1904-4068，男，博士，副教授，主要从事计算机辅助几何设计及其应用研究,E-mail: lijuncheng82@126.com.

基金项目：湖南省教育厅资助科研项目(14B099);湖南省自然科学基金资助项目(13JJ6081).

收稿日期：2015-08-19.