平面机构全变量优化设计方法研究

路遵友， 殷昌贵， 石　钰， 李爱莲， 黄建龙

(1.山东轻工职业学院 机电工程系， 山东 淄博 255300；

2.山东理工大学 农业工程与食品科学学院, 山东 淄博 255049；

3.兰州理工大学 机电工程学院, 甘肃 兰州 730050)



平面机构全变量优化设计方法研究

路遵友1， 殷昌贵2， 石钰1， 李爱莲1， 黄建龙3

(1.山东轻工职业学院 机电工程系， 山东 淄博 255300；

2.山东理工大学 农业工程与食品科学学院, 山东 淄博 255049；

3.兰州理工大学 机电工程学院, 甘肃 兰州 730050)

摘要：以曲柄摇杆机构为例，将全部杆长作为设计变量，根据各变量在设计范围内的不确定性，使从动件摇杆在主动件曲柄运动规律一定的前提下能准确按预定轨迹运动，以理论和实际运动轨迹之间偏差值的平方和最小为优化设计目标，建立了数学模型，并给出了两种优化设计方法——序列二次规划法和均匀设计法的优化过程.研究结果表明：两种方法均能达到更加良好的优化目标，设计精度均有大幅提高，优化过程也更加简便、可行.

关键词：优化设计； 序列二次规划法； 均匀设计法； 四杆机构

为确保运动的稳定性，平面机构设计中常要求主动件和从动件在运动轨迹上较多位置处都能最佳地逼近期望值，因此对机构进行优化设计显得非常重要. 由于传统和常用的优化设计方法中存在设计规范和设计参数经验取值的不确定性，就导致了设计的多解性，致使设计方案难以更好地符合客观实际规律. 针对这个问题，作为典型的平面四杆机构，曲柄摇杆机构的优化设计得到广泛的研究. 以曲柄摇杆机构的理论和实际运动轨迹之间偏差的平方和最小为设计目标，刘惟信利用惩罚函数法对曲柄摇杆机构的摇杆和连杆两个杆长作为设计变量进行了优化设计，并计算得到理论和实际运动轨迹间偏差的平方和最小为0.058 3[1]；而王富民等利用遗传算法与惩罚函数结合的方法对连杆和摇杆两个设计变量优化设计后得到的偏差的平方和最小数值为0.012 0[2];黄建龙等利用模糊理论进行的连杆和摇杆两个设计变量优化后得到的偏差的平方和最小数值为0.051 1[3];龚水明和尹君驰等各自利用MATLAB软件编程对连杆和摇杆两个设计变量优化后得到的偏差的平方和最小数值为0.068 8和0.067 8[4-5]. 为深化机械优化设计方法，本文将曲柄摇杆机构的全部4个杆长都作为设计变量，并分别给出利用目前较先进的序列二次规划法和从统计学领域引申出来的均匀设计法[6-7]进行优化的过程和结果分析，提出更加简单实用的设计思路和方法，以期得到理想的结果.

1优化设计数学模型

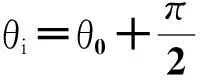
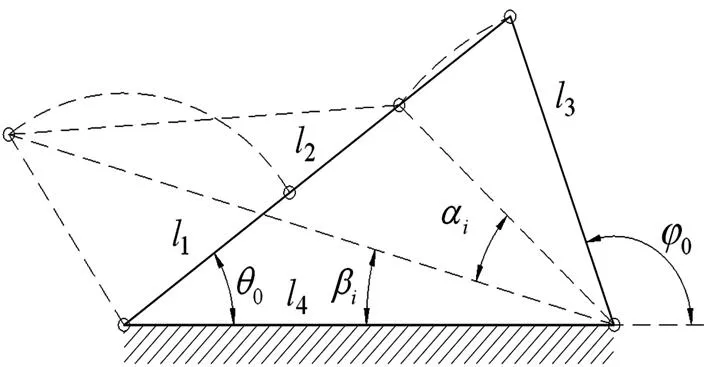
图1　曲柄摇杆机构简图

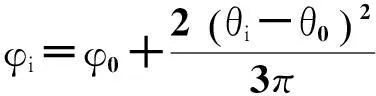
(1)

式中：θ0为曲柄的位置角；φ0为摇杆的位置角.

1.1选取优化设计变量

由文献[1-5]知，由图1可得如下关系式：

(2)

(3)

式中l1、 l2、 l3、l4均未知，则设计变量为

(4)

1.2确定优化设计目标函数

由设计变量的分析可知，对于本问题涉及到4个独立参数，因此，只能最大程度上近似实现设计要求，故目标函数可根据已知的运动规律和实际运动规律之间偏差值的平方和最小为目标来建立，即

(f)x=∑(φi-φni)2

(5)

式中：φi为摇杆l3的期望输出角， φni为实际输出角，其中

φni=π-αi-βi

(6)

(7)

(8)

(9)

1.3建立优化设计约束条件

优化设计所要考虑的约束主要是机构的传动性和设计变量的边界性. 因此，各设计变量的边界性应满足如下约束条件：

(1)杆长约束条件：l1≥0 ，l2≥0，l3≥0，

l4≥0.

(2)曲柄存在条件

(10)

(3)对于4个杆长变量，在进行设计前应根据曲柄存在条件设定其变化范围，不妨任意取

1≤l1≤2

2≤l2≤4

3≤l3≤5

4≤l4≤6

2序列二次规划法的优化设计分析

序列二次规划法是MATLAB软件优化工具箱中的一种算法，该算法适合求解非线性约束优化问题，其原理是将原非线性约束优化问题转化为一系列的二次规划子问题，再构造变尺度矩阵，最后调用fmincon函数来求解出该约束优化问题的最优解.本文将四杆长均作为变量进行优化，为得到优化结果，先通过MATLAB软件编写名为fourbarfun.m的程序文件，内容如下：

function f=fourbarfun(x)

f=0

a0=acos(((x(1)+x(2))^2-x(3)^2+x(4)^2)/(2*x(4)*(x(1)+x(2))))

b0=acos(((x(1)+x(2))^2-x(3)^2-x(4)^2)/(2*x(4)*x(3)))

fora=a0:pi/18:(a0+1.5707)

b=b0+2*(a-a0)^2/(3*pi)

r=sqrt(x(1)^2+x(4)^2-2*x(1)*x(4)*cos(a))

m=acos((r^2+x(3)^2-x(2)^2)/(2*r*x(3)))

n=acos((r^2-x(1)^2+x(4)^2)/(2*x(4)*r))

bb=pi-m-n

i=(bb-b)^2

f=f+i

end

编写名为fourbarcon.m的程序文件，内容如下：

function [c,ceq]= fourbarcon(x)

c=[x(2)^2+x(3)^2-1.414*x(2)*x(3)-(x(1)-x(4))^2;(x(1)+x(4))^2-x(2)^2-x(3)^2-1.414*x(2)*x(3)];

ceq=[]

编写好上面的两个文件并打开后，再根据约束条件及优化目标函数在MATLAB软件的Command Window窗口输入如下优化计算的程序语句：

x0=[2,3,4,5];

A=[11 -1 -1;1 -1 1 -1;1 -1 -1 1];

b=[0;0;0];

lb=zeros(3,1);

options=optimset('largescale','off');

[x,fval]=fmincon(@fourbarfun,x0,A,b,[],[],lb,[],@ fourbarcon,options)

运行后结果如下

x =1.53183.04264.09605.0755

fval =0.0018

结果显示对于四变量的曲柄摇杆机构，SQP算法优化后的四杆长分别为l1=1.531 8，l2=3.042 6，l3=4.096 0，l4=5.075 5，满足约束条件要求，此时得到的偏差值的平方和为f(x)=0.001 8.

3均匀设计法的优化设计分析

均匀设计法是当前统计学领域最先进的试验设计方法，该设计方法适用于多因素和多水平的试验设计条件，利用该方法能使试验点在多维空间内均匀分散，并让有限的数据有较强的代表性，从而大幅减少试验次数.均匀设计法的基本设计思路是根据预定试验的因素数和水平数，利用好格子点法构造均匀设计表，再选用“均匀设计表”，最后确立各次试验的条件和顺序并进行试验，获得试验数据.

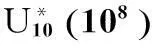
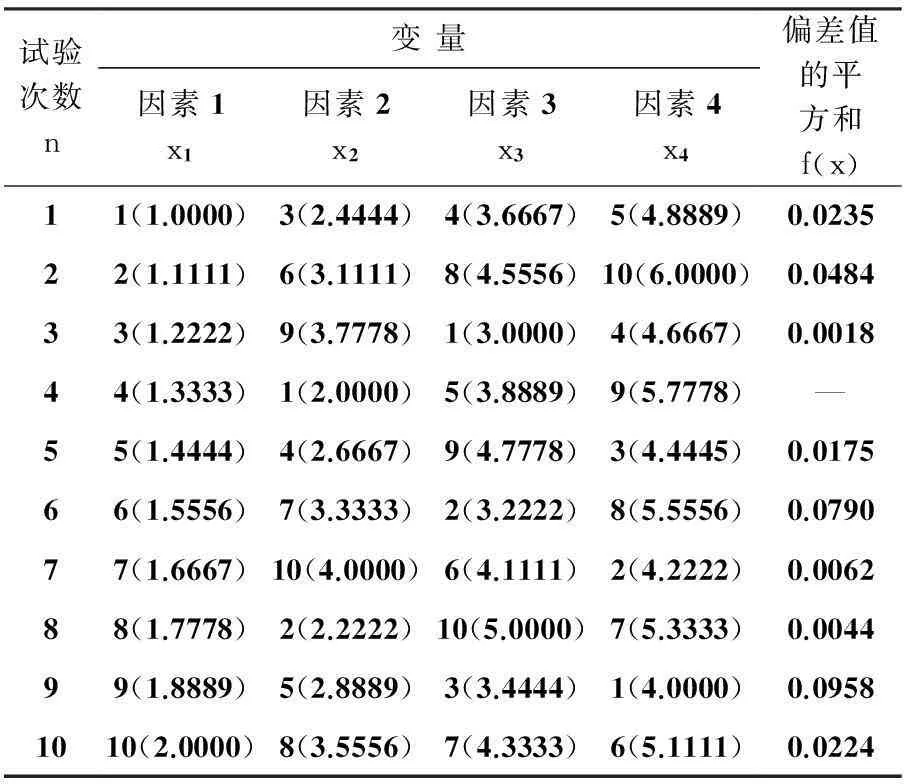
试验次数n变量因素1x1因素2x2因素3x3因素4x4偏差值的平方和f(x)11(1.0000)3(2.4444)4(3.6667)5(4.8889)0.023522(1.1111)6(3.1111)8(4.5556)10(6.0000)0.048433(1.2222)9(3.7778)1(3.0000)4(4.6667)0.001844(1.3333)1(2.0000)5(3.8889)9(5.7778)—55(1.4444)4(2.6667)9(4.7778)3(4.4445)0.017566(1.5556)7(3.3333)2(3.2222)8(5.5556)0.079077(1.6667)10(4.0000)6(4.1111)2(4.2222)0.006288(1.7778)2(2.2222)10(5.0000)7(5.3333)0.004499(1.8889)5(2.8889)3(3.4444)1(4.0000)0.09581010(2.0000)8(3.5556)7(4.3333)6(5.1111)0.0224

通过表1中数据可以看出，当进行到第3次试验时，即可得到试验方案中最小的目标函数值，即在x1=1.222 2，x2=3.777 8，x3=3.000 0，x4=4.666 7时，此时偏差值的平方和f(x)=0.001 8.

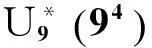
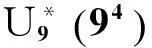
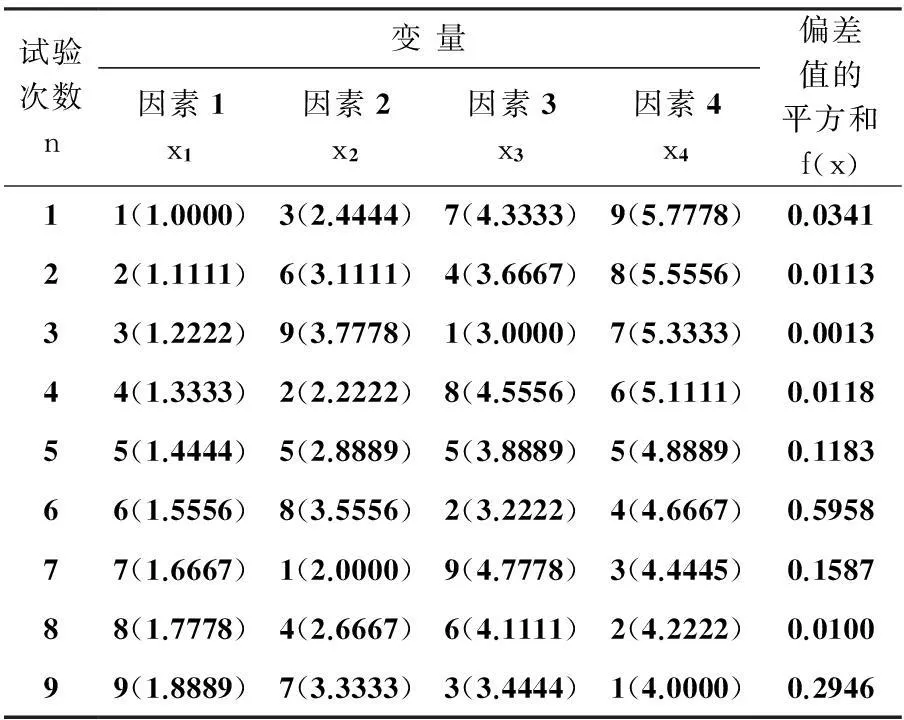
试验次数n变量因素1x1因素2x2因素3x3因素4x4偏差值的平方和f(x)11(1.0000)3(2.4444)7(4.3333)9(5.7778)0.034122(1.1111)6(3.1111)4(3.6667)8(5.5556)0.011333(1.2222)9(3.7778)1(3.0000)7(5.3333)0.001344(1.3333)2(2.2222)8(4.5556)6(5.1111)0.011855(1.4444)5(2.8889)5(3.8889)5(4.8889)0.118366(1.5556)8(3.5556)2(3.2222)4(4.6667)0.595877(1.6667)1(2.0000)9(4.7778)3(4.4445)0.158788(1.7778)4(2.6667)6(4.1111)2(4.2222)0.010099(1.8889)7(3.3333)3(3.4444)1(4.0000)0.2946

通过表2中数据可以看出，当进行到第3次试验时，即可得到试验方案中最小的偏差值，即在x1=1.222 2，x2=3.777 8，x3=3.000 0，x4=5.333 3时，此时偏差值的平方和为f(x)=0.001 3，得到的目标函数值更小，结果更好.

4结束语

通过序列二次规划法对本文的数学模型进行四变量优化设计，从优化结果可以看出，该方法能使得机构理论运动轨迹和实际运动轨迹之间偏差的平方和达到0.001 8，相对于文献[1-5]中对于两参数的设计优化最小结果0.012 0，设计精度提高了85%，效果明显.

均匀设计法能将设计变量的试验数据在设计范围内高度均匀分散，并能大幅度减少试验次数.从优化结果上可以看出，采用均匀设计法来优化产生设计变量的初始群体的数值，通过试验的方法将数值带入目标函数进行计算能达到优化设计变量的目的，本文对于同一个数学模型，仅仅通过有限的试验次数就能使得机构已知运动轨迹和实际运动轨迹之间偏差的平方和达到0.001 8，甚至达到0.001 3的设计精度，不但比遗传算法和惩罚函数法结合的方法设计精度提高了89.2%，还比本文应用的序列二次规划法的优化设计精度提高了27.8%，更加充分体现了均匀设计法的优越性.

参考文献:

[1] 刘惟信.机械最优化设计[M]. 北京：清华大学出版社，1994.

[2] 王富民,张扬,田社平.遗传算法与惩罚函数法在机械优化设计中的应用[J]. 中国计量学院学报， 2004(4)：290-293.

[3] 黄建龙,路遵友. 基于模糊集理论的四杆机构优化设计[J]. 兰州理工大学学报，2007，33(1)：37-39.

[4] 龚水明,詹小刚.基于MATLAB优化工具箱的机械优化设计[J]. 机械工程师，2008(10)：92-94.

[5] 尹君驰,黄勇.MATLAB在机械优化设计中的应用[J]. 科技创新与应用，2012(17)：65-66.

[6] 方开泰.均匀设计与均匀设计表[M]. 北京：科学出版社，1994.

[7] 方开泰.均匀设计及其应用[J]. 数理统计与管理，1994(1)：57-63.

[8] 郑文纬，吴克坚.机械原理[M]. 北京：高等教育出版社，2002.

[9] 陈水利，李敬功.模糊集理论及其应用[M]. 北京：科学出版社，2005.

[10] 邱宣怀. 机械设计[M]. 北京：高等教育出版社，1997.

(编辑：郝秀清)

All design variables optimization of the plane mechanism

LU Zun-you1, YIN Chang-gui2, SHI Yu1, LI Ai-lian1, HUANG Jian-long3

(1. Department of Mechanical and Electrical Engineering, Shandong Vocational College of Light Industry, Zibo 255300, China;2. School of Agricultural Engineering and Food Science, Shandong University of Technology, Zibo 255049, China;3. College of Mechano-Electronic Engineering, Lanzhou University of Technology, Lanzhou 730050, China)

Abstract:Taking crank and rocker mechanism as an example and according to the uncertainty of design variables of the mechanism to be designed, all the rod length were used as the design variables with uncertainty in their each range, the driven rocker was made move exactly in accordance to a definite pattern specified by the motion pattern of driving crank. Taking the minimized sum of squares of deviation between theoretical and actual motion patterns as designing objective, a mathematical model was set up, and sequential quadratic programming method and uniform design method were used to design and optimize the model. Compared with other optimization methods, the results showed that sequential quadratic programming method and uniform design method used in this paper were simple and feasible to get better optimization objective and greatly improve the precision of design.

Key words:optimization design; sequential quadratic programming method; uniform design; four-bar linkage

中图分类号：TH122

文献标志码：A

文章编号：1672-6197(2016)04-0075-04

作者简介：路遵友，男，sdlivclzy@126.com

收稿日期：2015-04-27