非均衡湍流边界层脉动压力测试研究

庞业珍，俞孟萨

（中国船舶科学研究中心 船舶振动噪声重点实验室，江苏无锡 214082）

非均衡湍流边界层脉动压力测试研究

庞业珍，俞孟萨

（中国船舶科学研究中心 船舶振动噪声重点实验室，江苏无锡 214082）

通过建立非均衡湍流边界层脉动压力测试技术及可提供较高测试信噪比的低噪声风洞试验装置，采用表面贴装式硅微传声器线列阵，测量获得了不同压力梯度模型的湍流边界层脉动压力特性，压力梯度模型表面湍流边界层脉动压力低频平台区幅值增加3-5 dB；回归得到了非均衡湍流边界层流脉动压力频谱与Strauhal数及Re数和压力梯度相关的拟合模型，具有一定的适用性；压力梯度对湍流边界层脉动压力频率—波数谱的影响主要集中在300 Hz以下的低频段，传输波数附近峰脊区谱级增加3-5 dB。

非均衡湍流；边界层脉动压力；波数—频率谱

0 引 言

舰船水下航行器随着航速的提高及机械噪声和螺旋桨噪声的有效控制，水动力噪声将成为辐射噪声和声呐自噪声的主要声源[1]。为了有效合理预报舰船与水下航行器辐射噪声的水动力噪声分量，需要已知表面湍流边界层脉动压力作为输入参数[2]。由于湍流边界层脉动压力为时空随机分布的激励源，目前条件下，采用数值计算方法获取湍流边界层脉动压力的激励特性，相应计算模型尚不成熟，仍然需要采用模型试验的途径获取。

早在上世纪六十至八十年代，国外开展了大量湍流边界层脉动压力试验研究，在此基础上，建立了若干湍流边界层脉动压力频率—波数谱模型[3]，如Corcos模型[4]、Martin和Leehey模型[5]、Chase模型[6]、Smolyakav-Tkachenko模型以及Efimtsov模型[7]。针对低Ma数和光滑刚性平面物面，湍流边界层脉动压力测量有向低波数扩展的趋势。Corcos等研究了传感器形状对波数域接收响应的影响[8-11]；Pompel和Wooh[12]采用矩形、菱形、圆形换能器单元重叠的接收阵和SinC形状换能器，抑制接收灵敏度旁瓣，提高接收阵的空间增益。为了提高湍流边界层脉动压力测量的空间分辨率，Sherman[13]、Farabee[14]、Leclercq和Bohineust[15]、Arguillat和Ricot等[16-17]分别采用传感器阵列测量湍流边界层脉动压力，获得了一维、二维方向的湍流边界层脉动压力波数—频率谱。水中湍流边界层脉动压力测量受到越来越多的重视，Ciappi[18]和 Kimberly[19]分别测量了拖曳阵和高速船表面的湍流边界层脉动压力特性，Brungart[20]测量了水中渗和高分子溶液对湍流边界层脉动压力的影响。葛辉良[21]采用PVDF水听器在水洞中测量湍流边界层脉动压力归一化频谱，表明其能量分布特征以及量值都与空气中测量结果相吻合。Abraham和Keith[22]、Manoha[23]在水洞中采用传感器阵列测量湍流边界层脉动压力的频率—波数谱，表明在低频段的低波数和传输波数分量与Chase模型吻合较好。测量湍流边界层脉动压力不仅取决于Re数大小，还与物面压力梯度及弹性和柔性等物理特性有关。Schloemer[24]给出了三种压力梯度情况下的脉动压力频率谱的测试结果。Dowling[25]研究了弹性壁面和柔性壁面对湍流边界层脉动压力的影响。Farabee[26]和Brungart[27]分别试验测量了倾斜平板和台阶平板的非均衡湍流边界层脉动压力的频谱特性，Camussia[28]试验研究了不连续间断对边界层脉动压力的影响。

虽然针对压力梯度下非均衡湍流边界层脉动压力已经有诸多人进行相关研究，但尚未有公开成熟的压力梯度下湍流边界层脉动压力模型。考虑到舰船和水下航行器表面大部分区域的流动分布都是存在压力梯度，为了较为精确地计算水动力噪声，有必要测量不同压力梯度条件下的湍流边界层脉动压力特性。

本文综合考虑声学与流场性能要求，设计低噪声直流小风洞试验装置[29]，实现安静测试环境；通过计算筛选设计四种具有不同压力梯度的翼型模型并确定传感器安装位置，采用硅微传声器作为湍流边界层脉动压力测试传感器[30]，并基于印刷电路板技术设计制作21元传感器阵列，在低噪声风洞试验段测量不同势流压力梯度的非均衡湍流边界层脉动压力空间相关函数和空间互功率谱密度，采用时间—空间Fourier变换计算湍流边界层脉动压力频率谱和波数—频率谱并进行归一化，得到了湍流边界层脉动压力频谱密度函数与压力梯度参数的拟合模型。

1 测量装置及传感器阵列

为了实现安静测试环境，采取综合噪声控制措施设计建造了低噪声直流式小风洞（图1）。低噪声直流式小风洞由进口段、收缩段、试验段、扩散段、拐角段、消声段、过渡段、软接头和动力段组成，轴线展开长度总计20 m。试验段长2.4 mm、截面0.4×0.6 mm。针对风洞试验段背景噪声产生的多种途径，采取了风管消声、风机隔声、室外风道隔声以及风管隔振等噪声控制措施。其一、采用正弦形式声流式消声器、微穿孔板消声器及消声弯头抑制风机噪声沿风管传播；其二、风机周围分别采用砖墙，水泥板等隔声层，阻隔风机噪声传入风洞进风口方向及风管布置房间和试验段；其三、风管隔振安装。经测试，风洞最大试验风速32 m/s时，试验段最大背景噪声谱级为52 dB，使湍流边界层脉动压力测试信噪比可大于20 dB。

针对测量湍流边界层脉动压力的空间相关函数和互功率谱密度函数，采用Knowles公司生产的接收孔直径为1.02 mm的硅微传声器，设计了21元的传感器阵列，阵列长105 mm，传感器间距为5 mm，灵敏度偏差小于±1 dB、相位差小于2°。传感器阵列采用工业流水线加热焊接方式，将传感器固定在电路板上。阵列信号线、电源线、地线采用26孔插头引出，通过数据总线供电及传输信号。在电路板表面覆盖一层与传感器等高的塑料板，保证表面齐平，再将电路板嵌入到安装模板中，可整体安装在测量模型上（图2）。这种传感器阵列具有单元孔径小、幅度和相位灵敏度一致性高、阵列波数旁瓣抑制性能好、整体性好、表面平整光顺，便于安装等特点。

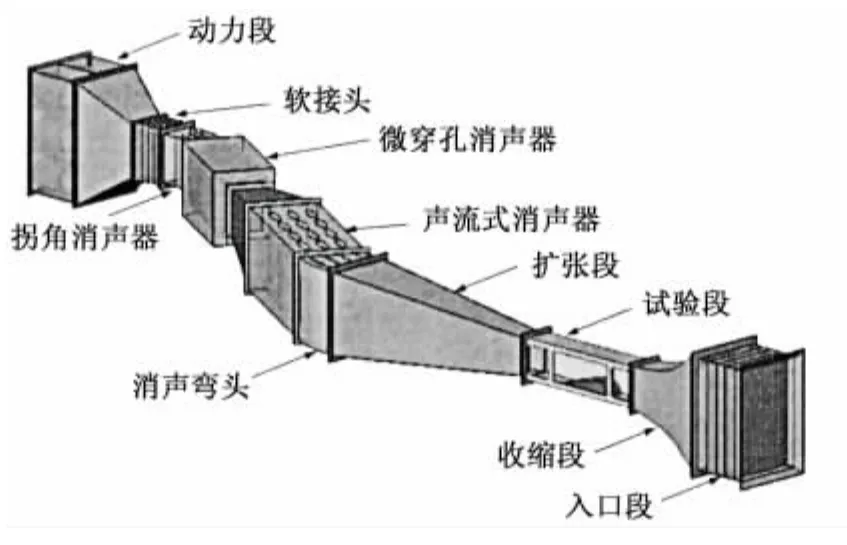
图1 低噪声风洞示意图Fig.1 Diagram of low noise wind tunnel

图2 硅微麦克风阵列（21元）Fig.2 MEMS Sisonic microphone array(21 cells)

2 测量模型及方法

选用NACA翼型，采用经验公式和CFD方法计算表面速度分布及压力梯度，设计了3个不同模型作为压力梯度的试验模型，并设计了一种平板模型作为无压力梯度模型。模型长度为1.1 m，宽度0.4 m，与风洞试验段宽度一致。在每个翼型收缩段模型表面布置8个动压测量点，在低噪声风洞利用PSI公司电子扫描压力测试系统测量了不同风速下的表面压力分布特性。试验风速从19 m/s至32 m/s，试验Re数大于临界Re数，传感器阵列安装位置处（图3中测点5位置）Re数1.4×106～2.3×106。试验结果表明，四种模型的压力梯度基本为常数，平板压力梯度系数略低于0，三种负压梯度模型压力梯度系数位于0.6-1.4之间，模型表面斜率越大，测点处压力梯度系数越大。

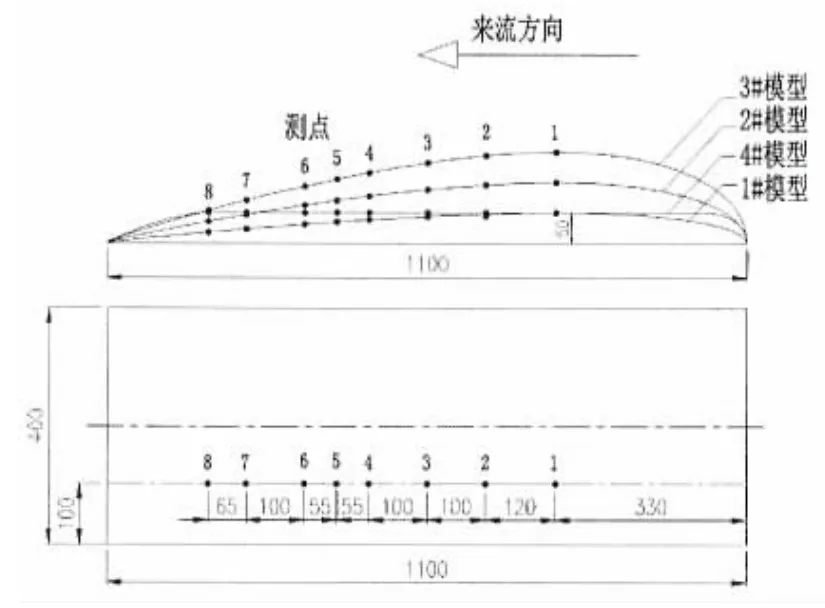
图3 动压测点位置Fig.3 Dynamic pressure test location

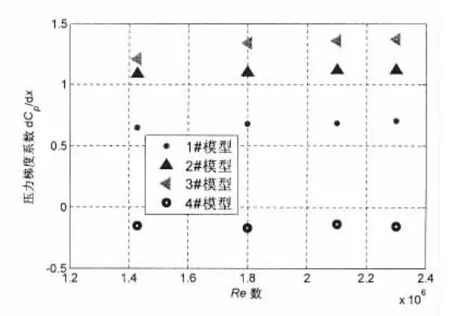
图4 脉动压力测点弦向压力梯度Fig.4 Pressure gradient at the turbulence boundary layer fluctuations test location

常用湍流边界层脉动压力波数—频率谱分析方法有两种，一种是Corcos互谱法，另一种是阵列空间傅里叶变换法。

1962年，Willmarth等[31]总结了Corcos采用的湍流边界层脉动压力波数—频率谱测量的互谱方法。这个方法对于测量位于高波数区的迁移峰效果很好，但分析包含声振信息的低波数区效果并不好。Corcos方法首先需要测量相干函数，相干函数可以由参考点自谱与两测点互谱得到。通过变化间距和分析频率所得到的相干函数进行拟合，可以得到此空间范围内的相干函数随无量纲数ωξ/Uc的变化曲线及表达式。将参考点自功率谱和相干函数拟合出的表达式共同计算互功率谱，然后对其进行空间傅立叶变换，就可以得到波数—频率谱。

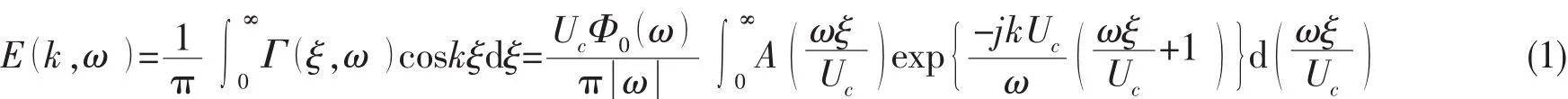
其中：ξ为两测点间距，Γ（ω，ξ）为间距ξ两点互功率谱，Φ0（ω）为参考点自功率谱，-ωξ/Uc代表由间距ξ引起的相移。

Corcos方法主要适用于传感器较少，无法同步测试不同间距下互谱的情况。随着多通道同步测试技术的发展以及快速傅里叶变换技术的发展，直接采用湍流边界层脉动压力传感器阵列进行时间—空间傅里叶变换可以更加容易获得波数—频率谱，这个方法称为阵列法[19]。

对于一维线阵，时间变量为t，空间变量x，湍流边界层脉动压力波数—频率谱由下式计算：

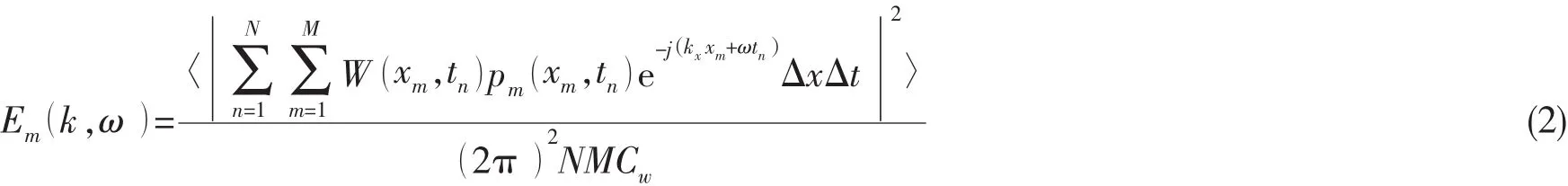
其中：〈〉代表期望值，pm为第m个传感器测量边界层压力时间序列，Δx为空间采样间隔（即传感器间距），xm=（m-1） Δx，Δt为时间采样间隔，tn=（n-1） Δt，W（xm，tn）=Wx（xm）Wt（tn），Wt（tn）是时间窗，Wx（xm）为空间窗，N为空间采样点数，为窗常数。

对于等间距线阵，其间距为d，传感器数量M，由Shannon采样定理可知无混叠域为 （-π/d，π/d），分析精度为2π/Md。可见受传感器单元数量限制，阵列法虽然可以分析低波数谱，但是波数—频率谱空间分辨率较低，且受到空间采样率限制，波数—频率谱在波数域上存在分析上限。采用间距5 mm的21元阵进行阵列法测量时，有效测试无混叠波数域为（-628 m-1，628 m-1），波数分析精度为59 m-1。

3 测量结果

3.1 模型试验概况

试验时，传感器安装中心位置位于距离首部0.705 m，约为模型总长度的0.65倍处（图3测点5附近），试验风速12～32 m/s。4#平板模型作为无压力梯度模型，湍流边界层脉动压力试验结果与1#-3#三个压力梯度模型试验结果进行比较。

图5 阵列安装位置Fig.5 Location of microphone array

3.2 非均衡湍流边界层脉动压力频率谱特性

针对湍流边界层脉动压力的时空随机性，测试获得了三个有压力梯度模型和一个无压力梯度模型的湍流边界层脉动压力自功率谱，并采用φm（ω） U0/q2δ*和ωδ*/U0对湍流边界层脉动压力自功率谱曲线的纵坐标和横坐标进行归一化处理，得到湍流边界层脉动压力归一化自功率谱，其中δ*为排挤厚度，q为动压，U0为来流流速。测量结果表明：湍流边界层脉动压力自功率谱级在ωδ*/U0为1-1.5以下的低频段随频率基本不变，近似呈为一水平线，在ωδ*/U0为1-1.5以上的高频段，谱级以一定的斜率随频率下降，动压归一化处理的湍流边界层脉动压力均方根值在0.01～0.025之间（图6），归一化自功率谱级为－30 dB左右，符合湍流边界层脉动压力的基本特性（图7）。进一步分析归纳了压力梯度对湍流边界层脉动压力的影响规律，可以看到在湍流边界层脉动压力低频区，模型压力梯度越大，自功率谱级越大，有压力梯度模型比无压力梯度模型的湍流边界层脉动压力自功率谱级普遍大3～5 dB。有压力梯度模型的归一化湍流边界层脉动压力自功率谱级平台区范围变小到ωδ*/U0约为0.6，且有压力梯度模型的湍流边界层脉动压力自功率谱级受测点Re数的影响较大，不同测点位置的湍流边界层脉动压力自功率谱级发散性随模型压力梯度增大而增大。

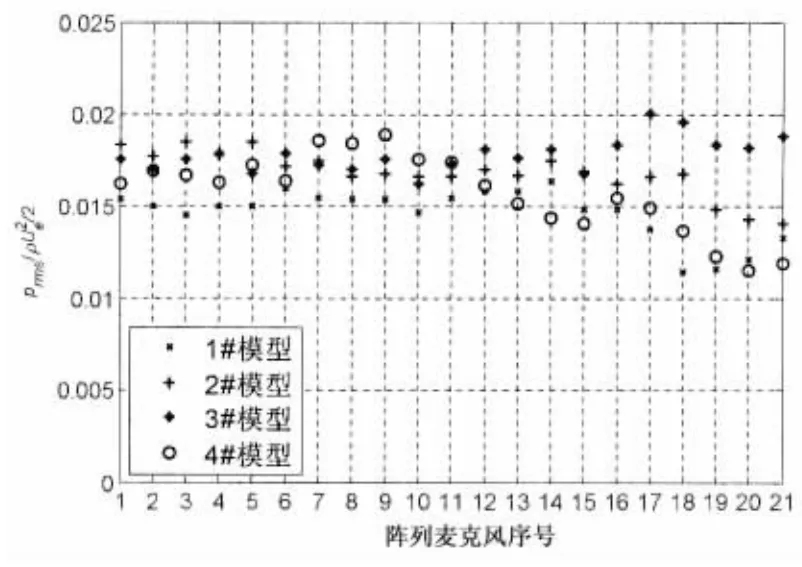
图6 动压归一化湍流边界层脉动压力均方根值（29 m/s）Fig.6 RMS normalized turbulent boundary layer fluctuations by dynamic pressure(29 m/s)

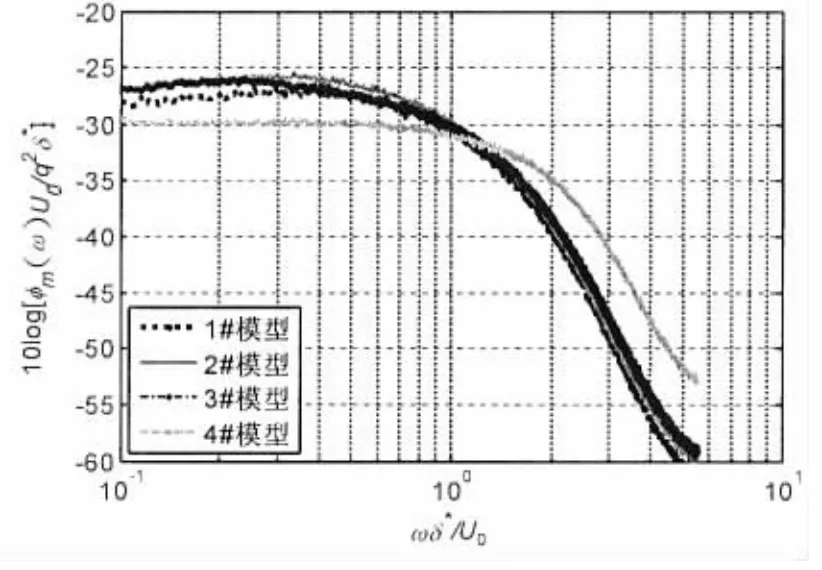
图7 四种模型归一化湍流边界层脉动压力 频率谱比较（19 m/s）Fig.7 Normalized turbulent boundary layer fluctuations pressure spectrum of 4 models(19 m/s)

3.3 非均衡湍流边界层脉动压力频谱拟合模型

对有压力梯度模型湍流边界层脉动压力归一化频谱建模，基于湍流边界层脉动压力自功率谱的基本关系，考虑压力梯度的影响因子，得到适合不同压力梯度的湍流边界层脉动压力归一化频谱拟合解析表达式。

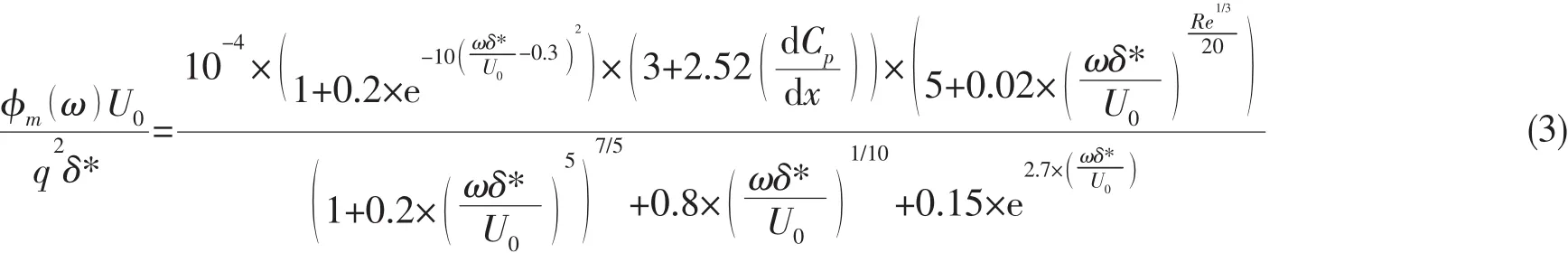
式中：Cp为压力分布函数，表示压力梯度项。

针对三种有压力梯度测量模型，由（3）式计算不同测量风速下的湍流边界层脉动压力归一化功率谱表明了（3）式的适用性，计算与测试结果吻合较好，参见图8。

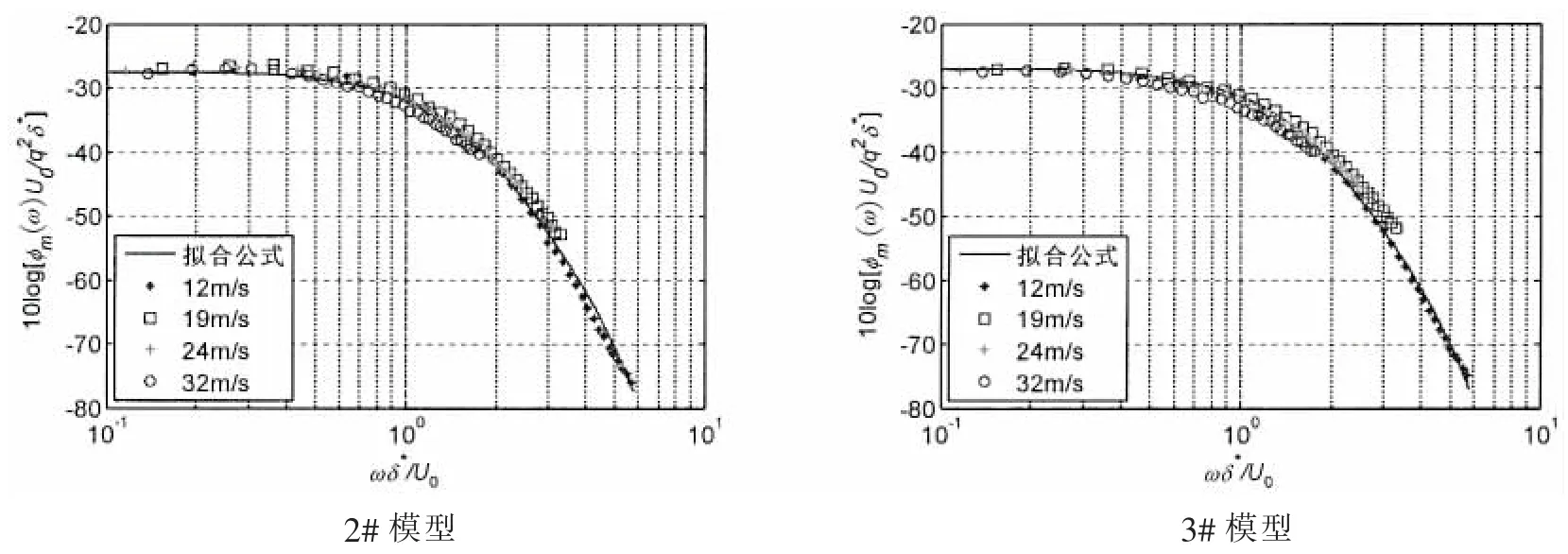
图8 有压力梯度模型湍流边界层脉动压力归一化频谱级拟合与测试结果比较Fig.8 Fitted curve and measurement result of normalized turbulent boundary layer fluctuation pressure spectrum of wing models with pressure gradients

3.4 非均衡湍流边界层脉动压力波数—频率谱特性

基于湍流边界层脉动压力测量的阵列法，采用传感器阵列测量的3个有压力梯度模型和一个无压力梯度模型的湍流边界层脉动压力时间序列，分析得到湍流边界层脉动压力空间相干函数和波数-频率谱。结果表明：测点间距越远，相应的湍流边界层脉动压力空间相干系数越小，对于给定测点间距，空间相干系数随频率近似呈指数规律下降的特征（图9）。湍流边界层脉动压力频率-波数谱在传输波数kc=ω/Uc位置上出现明显的峰脊（图10）。峰脊位置随频率增加向高波数迁移，且其范围随风速增加而扩大。风速一定时，湍流边界层脉动压力频率—波数谱峰脊值随着频率的增加而减小。

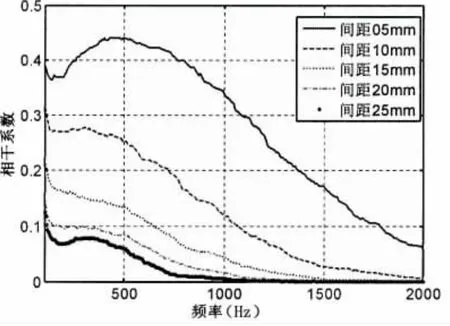
图9 相干系数（1#模型，29 m/s）Fig.9 Coherence of microphones(Model 1,29 m/s)

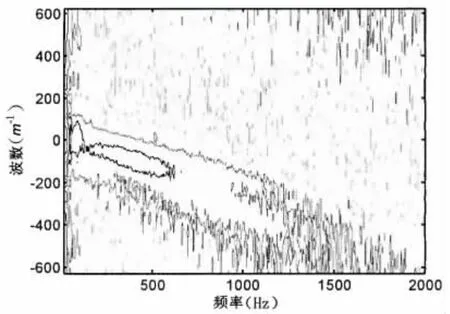
图10 波数—频率谱（1#模型，29m/s）Fig.10 Wavenumber-frequency spectrum(Model 1,29m/s)

在湍流边界层脉动压力传输波数附近的峰脊区，模型表面压力梯度使湍流边界层脉动压力的波数—频率谱谱级增加3～5 dB，压力梯度对湍流边界层脉动压力频率—波数谱的影响主要集中在300 Hz以下的低频段（图11）。

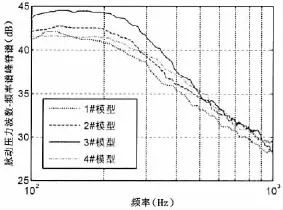
图11 不同模型湍流边界层脉动压力波数—频率谱峰脊谱级比较（12 m/s）Fig.11 The wavenumber-frequency spectrum peak value of turbulent boundary layer fluctuation pressure of various models(12 m/s)

4 结 论

通过建立非均衡湍流边界层脉动压力测试技术及可提供较高测试信噪比的低噪声风洞试验装置，采用表面贴装式硅微传声器线列阵，测量获得了压力梯度对模型的非均衡湍流边界层脉动压力特性，模型表面压力梯度对湍流边界层脉动压力低频平台区的幅值影响明显，约增加了3-5 dB，回归得到了非均衡湍流边界层流脉动压力频谱与Strauhal数ωδ*/U0及Re数和压力梯度参数相关的拟合模型，具有一定的适用性；压力梯度对湍流边界层脉动压力频率—波数谱的影响主要集中在300 Hz以下的低频段，传输波数附近峰脊区谱级增加3-5 dB。湍流边界层频率—波数谱测量与分析，受环境背景噪声的影响较敏感，压力梯度对湍流边界层脉动压力频率—波数谱中低波数分量的影响规律，还需要进一步测量分析研究。

[1]俞孟萨,吴有生,庞业珍.国外舰船水动力噪声研究进展概述[J].船舶力学,2007,11(1)：152-158. Yu Mengsa,Wu Yousheng,Pang Yezhen.A review of progress for hydrodynamic noise of ships[J].Journal of Ship Mechanics,2007,11(1)：152-158.

[2]穆宁A T.航空声学[M].曹传锋译.北京：北京航空航天大学出版社,1993.

[3]Hwang Y F,Bonness W K,Hambric S A.Comparison of semi-empirical models for turbulent boundary layer wall pressure spectra[J].Journal of Sound and Vibration,2009,319(1-2)：199-217.

[4]Corcos G M.The structure of the turbulent pressure field in boundary-layer flows[J].Journal of Fluid Mechanics,1964, 18(3)：353-378.

[5]Martin N C,Lechey P.Low wave number wall pressure measurements using a rectangular membrane as a spatial filter[J]. J Sound and Vibration,1977,52(1)：95-120.

[6]Chase D M.The wave-vector-frequency spectrum of pressure on a smooth plane in turbulent boundary-layer flow at low mach number[J].J Acoust.Soc.Am.,1991,90(2)：1032-1040.

[7]Smol’yakav A V,Tkachenko V M.The measurement of turbulent fluctuation[M].Translated by Chomet S,Springer-Verlag,1983.

[8]Corcos G M.The resolution of turbulent Pressure at the wall of a boundary layer[J].J Sound and Vibration,1967,6(1)：59-70.

[9]Gerb F E.Measurements on the effect of transducer size on the resolution of boundary layer pressure fluctuations[J].J A-coust.Soc.Am.,1969,46(1)：253-261.

[10]White P H.Effect of transducer size shape and surface sensitivity on the measure meat of boundary layer pressure[J].J Acoust.Soc.Am.,1967,41(5)：1358-1363.

[11]Ko S H.Performance of various shapes of hydrophones in the reduction of turbulent flow noise[J].J Acoust.Soc.Am., 1993,93(3)：1293-1299.

[12]Pompel F J,Wooh S C.Phased array element shapes for suppressing grating lobes[J].J Acoust.Soc.Am.,2002,111(5)：2040-2048.

[13]Sherman C H,et al.Measurement of the turbulent boundary layer wave-vector spectrum[J].J Acoust.Soc.Am.,1990,88 (1)：386-390.

[14]Farabee T M,Geib F.E.Measurements of boundary layer pressure fluctuation at low wavenumbers on smooth and rough walls[J].Proceedings of the ASME Symposium on Flow Noise Modeling,Measurement,and Control,Noise Control and A-coustics,1991,l11：55-68.

[15]Leclercq D J J,Bohineust X.Investigation and modeling of the wall pressure field beneath a turbulent boundary layer at low and medium frequencies[J].J Sound and Vibration,2002,257(3)：477-501.

[16]Arguillat B,Ricot D.Measurements of the wavenumber-frequency spectrum of wall pressure fluctuations under turbulent flows[C]//11th AIAA/CEAS Aeroacoustics Conference(26th Aeroacoustics Conference).Monterey,California,May,2005. [17]Arguilla B,Ricot D.Measured wavenumber：Frequency spectrum associated with acoustic and aerodynamic wall pressure fluctuations[J].J Acoust.Soc.Am.,2010,128(4)：1647-1655.

[18]Ciappi E,Magionesi F.Characteristics of the turbulent boundary layer pressure spectra for high-speed vessels[J].Journal of Fluids and Structures,2005,21：321-333.

[19]Cipolla K M,Keith W L.Measurements of the wall pressure spectra on a full-scale experimental towed array[J].Ocean Engineering,2008,35：1052-1059.

[20]Brungart T A,et al.The scaling of the wall pressure fluctuations in polymer-modified turbulent boundary layer flow[J].J Acoust.Soc.Am.,2000,108(1)：71-75.

[21]葛辉良,何祚镛,暴雪梅.湍流边界层起伏压力谱和聚偏氟二乙烯薄膜(PVDF)水听器响应的实验研究[J].声学学报, 2009,25(5)：430-410. Ge Huiliang,He Zuoyong,Bao Xuemei.Experimental study on spectrum of turbulent-boundary-layer fluctuation pressure and response of a PVDF hydrophone[J].Acta Acoustica,2009,25(5)：403-410.

[22]Abraham B M,Keith W L.Direct measurements of turbulent boundary layer wall pressure wave number frequency spectra[J].J Fluids Eng.,1988,120：29-39.

[23]Manoha E.The wavenumber-frequency spectrum of the wall pressure fluctuations beneath turbulent boundary layer[J]. AIAA Paper 96-1758,1996.

[24]Schloemer H H.Effect of pressure gradients on turbulent boundary layer wall pressure fluctuations[J].J Acoust.Soc.Am., 1966,42(1)：93-113.

[25]Dowling A P.Flow-acoustic interaction near flexible wall[J].J Fluid Mech.,1983,128：181-198.

[26]Farabee T M.An experimental investigation of wall pressure fluctuations beneath non-equilibrium turbulent flows[D].Doctoral Dissertation,Catholic University of America,1986.

[27]Brungart T A,et al.Wall pressure fluctuations induced by separated-reattached channel flow[J].Journal of Sound and Vibration,2002,251(3)：558-577.

[28]Camussia R.Wall pressure fluctuations induced by turbulent boundary layers over surface discontinuities[J].Journal of Sound and Vibration,2006,294(1-2)：177-204.

[29]庞业珍,俞孟萨等.二维低噪声风洞设计[J].舰船科学技术,2011,33(3)：22-26. Pang Yezhen,Yu Mengsa,et al.Research on 2-D low-noise windtunnel design[J].Ship Science and Technology,2011, 33(3)：22-26.

[30]庞业珍,俞孟萨.湍流边界层脉动压力测量传感器列阵设计[C].中国造船工程学会学术论文集,编号：200704.西安, 2007. Pang Yezhen,Yu Mengsa.Sensor array design for turbulent boundary layer fluctuation pressure measurement[C].Proceedings of CSNAME,2007,Xi’An,200704：211-217.

[31]Willmarth,Wooldridge.Measurement of the fluctuating pressure at the wall beneath a thick turbulent boundary layer[J]. Journal of Fluid Mechanics,1962.

Research on fluctuation pressure test for nonequilibrium turbulence boundary-layer

PANG Ye-zhen,YU Meng-sa
(National Key Laboratory on Ship Vibration&Noise,China Ship Scientific Research Center,Wuxi 214082,China)

Fluctuation pressure test methods for Nonequilibrium turbulence boundary layer are researched, a low noise wind tunnel which provide high measurement signal-to-noise ratio is designed and built.MEMS microphone arrays are used to measure the turbulent boundary-layer fluctuation pressure of 4 wing models with various pressure gradients.Turbulent boundary-layer fluctuation pressure level of wing models with pressure gradient is increased by 3-5 dB over that without pressure gradient in low-frequency plateau region. Fitted equations of nonequilibrium turbulence boundary-layer fluctuation pressure spectrum related to Strauhal number,Reynolds number and pressure gradient are regressed with certain applicability.Influence of pressure gradient on turbulence boundary layer fluctuation frequency-wavenumber spectrum is basically below 300 Hz,and the peak spectral level near the transfer wavenumber increase 3-5 dB.

nonequilibrium turbulence;boundary layer fluctuation;frequency-wavenumber spectrum

O357

：Adoi：10.3969/j.issn.1007-7294.2016.05.001

1007-7294（2016）05-0515-08

2016-03-12

庞业珍（1982-），男，博士研究生，E-mail：chaos123@qq.com；俞孟萨（1960-），男，研究员，博士生导师。