在基本图形的导航下进行合理思考

☉浙江省宁波市鄞州实验中学　蔡卫兵



在基本图形的导航下进行合理思考

☉浙江省宁波市鄞州实验中学蔡卫兵

一、试题再现

题目如图1，在等腰直角三角形ABC中，∠ACB=90°，D是AB上任意一点（不与点A重合），连接DC，作DE⊥DC，EA⊥AC，DE与AE交于点E，则DE、DC有什么数量关系？请给出证明.

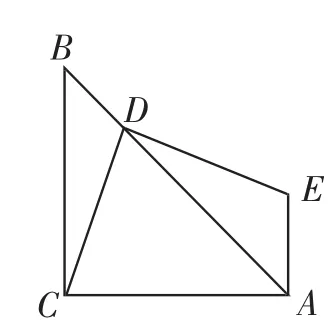
图1

本题既能反映学生对特殊图形性质的掌握程度，对全等三角形的判定与性质的运用能力，还能考查学生从特殊到一般进行探索、猜想、验证的数学思想方法和在复杂图形中提炼基本图形的能力.题目表述相对简约，问题的设置深浅有度，作为中考第一轮三角形基础复习时的每日一题，由学生在课外独立思考后，在第二天课堂中的前几分钟由一名学生主讲，其他学生进行补充或质疑，平时学生的参与热情很高，基本上能在较短的时间内顺利完成每日一题的讲题活动，但此次活动受阻，随机确定的前几个主讲同学只是凭直觉猜想DE=DC，但不知如何验证，有点出乎笔者的意料，为了引导学生顺利走出当前困境，进一步感悟在基本图形的导航下进行合理思考的解题方法，笔者开展了如下的解题教学.

二、解题教学

1.感知基本图形

师：如何猜想DE、DC的数量关系？你会进行怎样的操作？

生1：选择特殊位置，比如点D与点B重合，如图2，易证四边形ACDE为正方形.

生2：当D为AB的中点时，如图3，△CDE为等腰直角三角形，为此猜想DE=DC.

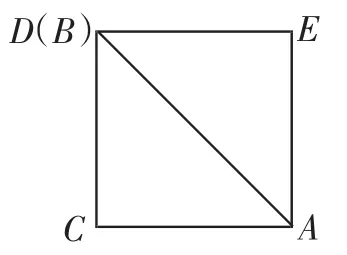
图2

师：这是从特殊到一般的数学思想方法，归纳猜想DE=DC，

那通常用什么方法来证明两条线段相等呢？

生（众）：全等或等腰.

师：如图2中可通过分别包含边DC、DE的两个三角形全等；如图3中可通过判定△DCE为等腰三角形.这是两个基本图形，形全等——线相等，形等腰——线相等.

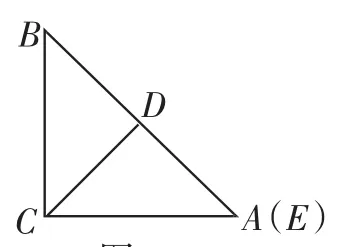
图3

师：在图1中，D是AB上任意一点时，能找出基本图形吗？

生3：考虑△BCD和△ADE全等.

生4：因为AD是随着点D的运动而变化，BC是固定的，所以考虑△BCD和△ADE全等的思路肯定是错的.

生5：连接CE，考虑△CDE为等腰直角三角形，但算不出∠DCE=45°.

2.聚焦基本图形

师：根据所给问题的条件和目标，那你应将解决问题的焦点聚集在什么地方？

生6：因为DC=DE，DC⊥DE，都跟点D有关，所以重点关注点D位置的特征.

师：点D位置有何特征？

生（众）：线垂直.

师：直角顶点处有我们经常遇到的基本图形吗？若找不到完整的基本图形，则尝试找到基本图形的一部分，并通过构造辅助线将其补全，接着能不能利用它？

生7：聚焦公共顶点的双直角的基本图形，如图4.

图4

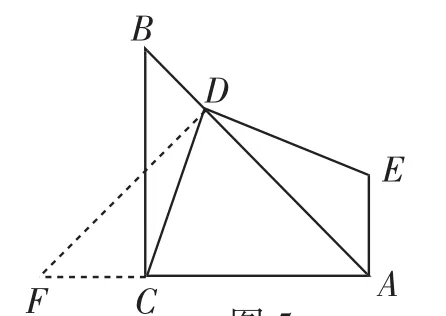
图5

解法1：如图5，过点D作DF⊥AB与AC的延长线交于点F.

因为DE⊥DC，所以∠FDC=∠ADE.因为EA⊥AC，所以∠F=∠DAE.又因为∠ACB=90°，AC=BC，所以∠DAF=45°，所以DA=DF.所以△FDC≌△ADE（ASA），所以DE=DC.

解法2：如图6，过点D作DF⊥AB与AE的延长线交于点F.同解法1得∠FDE=∠ADC，DF=DA，∠F=∠DAC，所以△FDA≌△ADC（ASA），所以DE=DC.

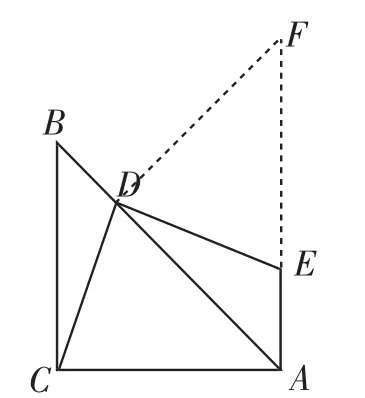
图6

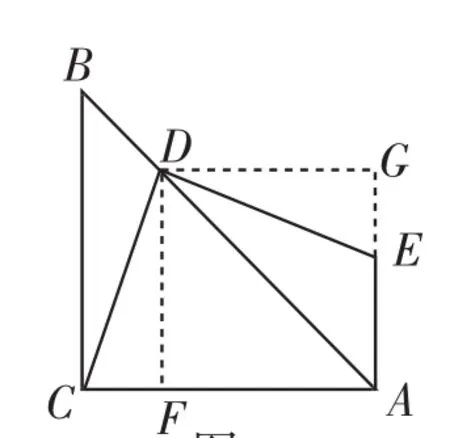
图7

解法3：如图7，过点D作DF⊥AC，DG⊥AE，垂足分别为F、G.由EA⊥AC，可知四边形AGDF为矩形，所以DG=FA.同解法1得∠CDF=∠EDG，所以Rt△CDF≌Rt△EDG，所以DE=DC.

生8：聚焦三边分别互相垂直的两个直角三角形的基本图形，如图8和图9.

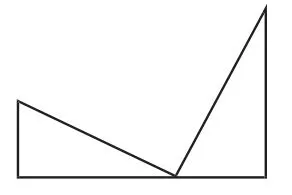
图8

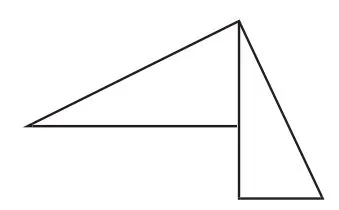
图9

解法4：如图10，过点D作GF⊥BC与BC交于点F，与AE的延长线交于点G.由∠ACB=90°，EA⊥AC，可知四边形ACGF为矩形，所以CF=GA.因为∠DAC=45°，所以∠DAE=45°，即△ADG为等腰直角三角形，所以AG=DG，所以CF=DG.由DE⊥DC，可证∠FCD=∠GDE，所以Rt△CDF≌Rt△DEG，所以DE=DC.

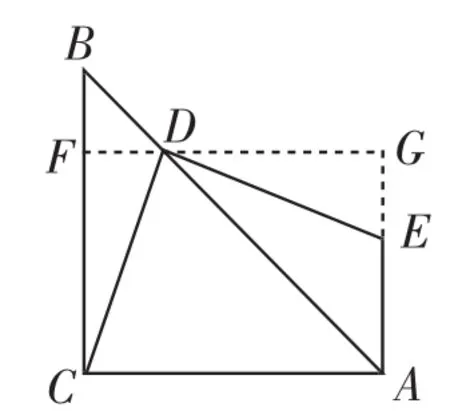
图10

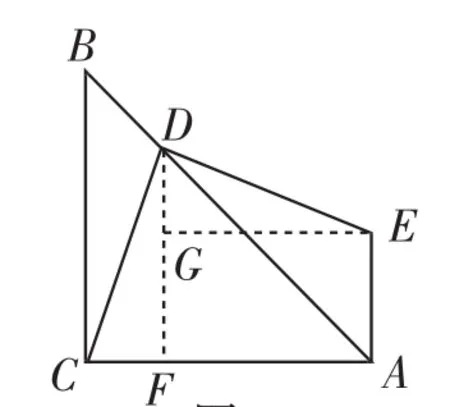
图11

解法5：如图11，过点D作DF⊥AC，垂足为F，过点E 作EG⊥DF，垂足为G.同解法4，可证Rt△CDF≌Rt△DEG，所以DE=DC.

解法6：如图12，过点C作CF⊥AB，垂足为F，过点E作EB⊥AB，垂足为G.因为∠DCF=∠EDG，∠CFD= ∠DEG=90°，所以Rt△CDF∽Rt△DEG，所以.由等腰直角△AFC和等腰直角△AEG，得CF=AF，EG=AG，所以，所以DF=AG=EG，所以Rt△CDF≌Rt△DEG，所以DE=DC.

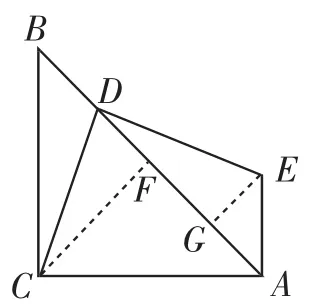
图12

生9：聚焦角平分、线相等、形翻折的基本图形，如图13.

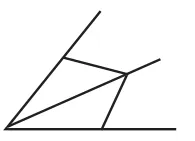
图13

解法7：如图14，在AC上截取一点F，使得AF=AE，连接DF.因为∠DAF=∠DAE=45°，AD=AD，所以△ADF≌△ADE，所以DF=DE，∠DFA=∠E.在四边形ACDE中，∠CDE=∠CAE=90°，所以∠DCA+∠E=180°，所以∠DCA+∠DFA=180°.因为∠DFC+∠DFA=180°，所以∠DCA=∠DFC，所以DC=DF，所以DE=DC.

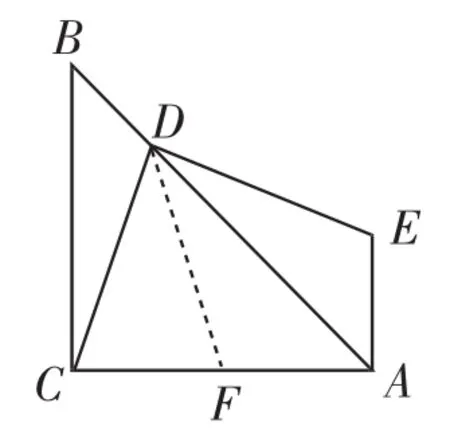
图14

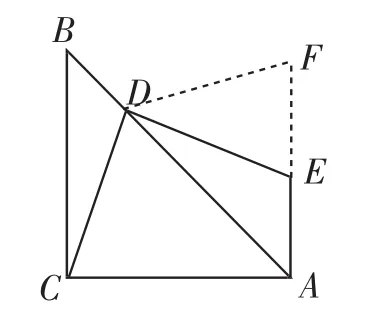
图15

解法8：如图15，在AE上截取一点F，使得AF=AC，连接DF.因为∠DAF=∠DAE=45°，AD=AD，所以△ADC≌△ADF，所以DC=DF，∠DCA=∠F.在四边形ACDE中，∠CDE=∠CAE=90°，所以∠DCA +∠DEA =180°.而∠DEA+∠DEF=180°，所以∠DEF=∠F，所以DF=DE，所以DE=DC.

生10：聚焦角直角、弦直径的基本图形，如图16和图17.

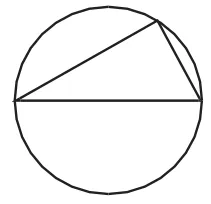
图16

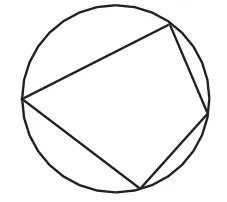
图17

解法9：如图18，连接CE，作△CDE的外接圆，因为DE⊥DC，所以CE为圆的直径.因为EA⊥AC，所以点A在CE为直径的圆上，即A、C、D、E在同一圆上.所以∠DEC= ∠DAC=45°，所以DE=DC.

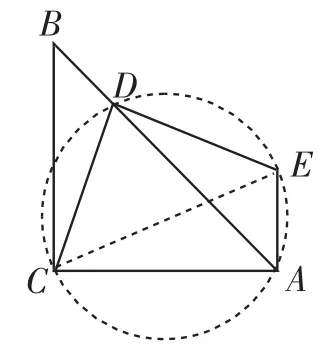
图18

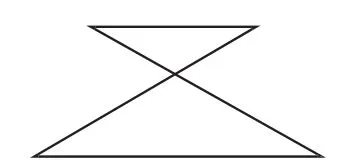
图19

生11：聚焦线平行、形相似的基本图形，如图19.

解法10：如图20，延长CD交AE的延长线于点F.由∠ACB=90°和EA⊥AC，得BC∥AF，所以△BCD∽△FDA，所以.由∠F=∠F，∠FDE =∠FAC =90°，得△FAC∽△FDE，所以，所以BC=AC，所以DE=DC.

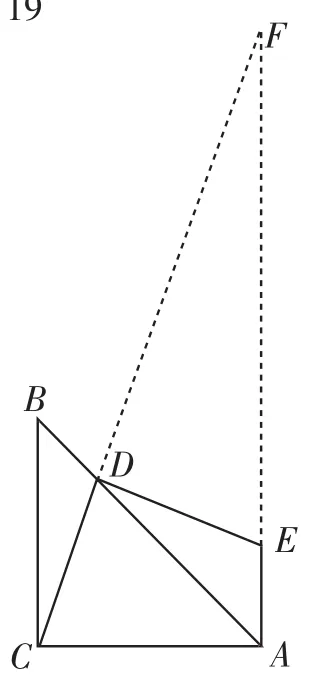
图20

3.演变基本图形

师：图形作为几何学科的研究对象，不论它多么复杂，都是由一个或者若干个最简单、最基本的图形组合而成，找到这些基本图形往往也就找到了解决问题的突破口.

话音刚落，生12起立，此题要分类讨论，因为点D为AB上任意一点，上述只证明了点D在线段AB中点上方的情形，当点D在线段AB中点的下方时，图形的位置发生了改变，如图21，所以有必要再加以说明.

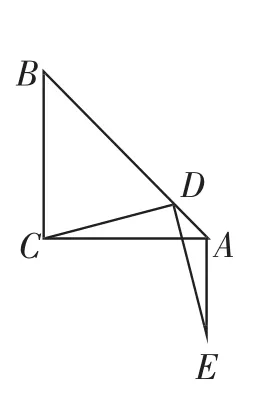
图21

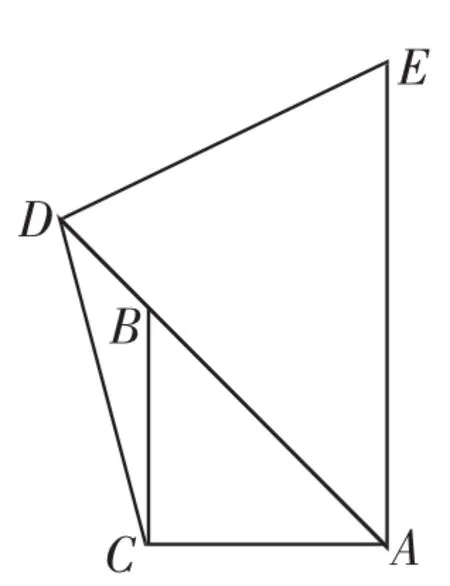
图22

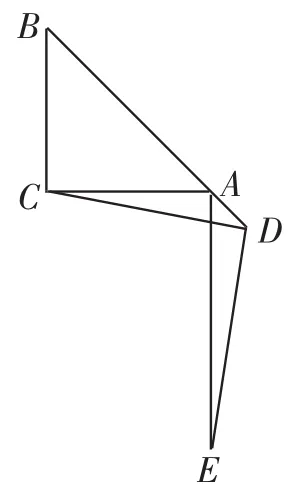
图23

生13：还是可用上述的证明方法，我认为当D为直线AB上任意一点（不与A重合），如图22和图23，DC=DE的结论仍然成立，而且这些证明方法都可通用.

师：前苏联数学家雅诺思卡娅曾说：“解题——就意味着把所要解决的问题转化为已经解决的问题.”在原题的探索、猜想、验证的过程中借助已解决的公共顶点的双直角的基本图形中的同角的余角相等，三边分别互相垂直的两个直角三角形的基本图形中的三角形相似，角平分、线相等的基本图形中的三角形全等，角直角、弦直径的基本图形中的四点共圆，线平行的“A”型和“X或Z”型中的三角形相似，分析图形并联想基本图形——作辅助线完善图形——利用基本图形发现思路，辅助线的添加是有理有据的.生12、生13又在已解决的基本图形的导航下进行合理思考，通过改变点D的位置进行演变图形.俗话说“变则通，通则久”，那你还能在此探究的基础上进一步尝试改编试题，使解题通法再延伸吗？

小组合作，不断提出延伸性问题：

问题1：在图7、图10、图11的导航下结合HL定理提出可交换问题的条件与结论，如图1，在等腰直角三角形ABC中，∠ACB=90°，EA⊥AC，D是AB上任意一点（不与A重合），若DC=DE，则DE、DC有怎样的位置关系？请给出证明.

问题2：在图5、图6、图7、图8、图10、图11、图20的导航下结合相似三角形的判定与性质或锐角三角函数提出改变条件探索结论，如图24，在△ABC中，∠ACB=90°，∠CBA=30°，D是AB上任意一点（不与A重合），连接DC，作DE⊥DC，EA⊥AC，DE与AE交于点E，则DE、DC有什么数量关系？请给出证明.

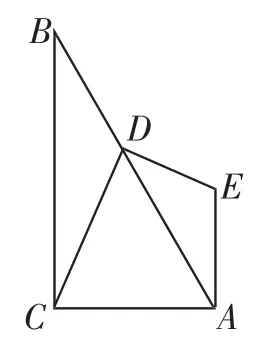
图24

图25

问题3：如图24，在△ABC中，∠ACB=90°，BC=nAC，D是AB上任意一点，连接DC，作DE⊥DC，EA⊥AC，DE与AE交于点E，则DE、DC有什么数量关系？请给出证明.

问题4：在图14、图15、图16的导航下结合圆的基本性质与解直角三角形提出改变图形探索条件，如图25，在△ABC中，∠ACB=90°，∠BAC=∠BAE=60°，D是AB上任意一点（不与A重合），连接DC，DE，当∠CDE为多少时DC=DE成立？请说明理由.

问题5：如图25，在△ABC中，∠ACB=90°，∠BAC=α，∠BAE=β，D是AB上任意一点（不与A重合），∠CDE+∠CAE=180°，请用含ɑ，β的三角函数表示

……

三、思考感悟

所谓基本图形就是将在“图形与几何”领域的学习过程中具有一定典型性的概念、公式、定理、例题、习题中反复出现、经常用到的对应图形，是结论化的图形，是图形化的公式.它作为构成几何图形的基本要素，如果能够从较复杂的图形中识辨、抽象、分离、构造出基本图形，借助基本图形中的基本元素及其相互关系进行思考，可以使抽象问题直观化，复杂问题简单化，提高学生对于图形与几何的学习水平，有利于发展学生的几何直观.因此，在几何的解题教学中，我们应重视重要结论所对应的基本图形的积累，重视引导学生分析图形并联想基本图形，在基本图形的导航下发现思路、作辅助线完善图形、解决问题、归纳规律、演变图形、拓展结论、图形重组等合理思考，从而发现“辅助线如何添”，顿悟“辅助性为何这样添”，明白“思路从哪里来”，领悟“问题到何处去”，真正为学生思维升华拓展空间.

参考文献：

1.高一子.基本图形在平面几何中的教学运用——以平行线的判定为例［J］.中学数学教学参考（中），2015（6）.

2.陈金红.模型出面繁简转换［J］.中学数学（下），2015（7）.