一道中考模拟压轴题的解法探究与思考

☉江苏省南京市中华中学上新河初级中学　宋伟军☉江苏省南京市中华中学上新河初级中学　黄玉华



一道中考模拟压轴题的解法探究与思考

☉江苏省南京市中华中学上新河初级中学宋伟军
☉江苏省南京市中华中学上新河初级中学黄玉华

在南京市组织的一次初三数学中考模拟练习中，一道压轴题让很多学生望而却步、思路受阻，得分率很低.笔者悉心研究发现，对于此题，只需抓住题目条件特征、图形特征和结论特征中的一个，运用基本数学模型和基本数学方法，即可自然求解.下面将解法探究呈现给大家，以飨读者.

一、题目

如图1，已知直线l与线段AB平行，试只用直尺作出AB的中点.

1.初步探索

如图2，在直线l的上方取一个点E，连接EA、EB，分别与l交于点M、N，连接MB、NA，交于点D，再连接ED并延长交AB于点C，则C就是线段AB的中点.

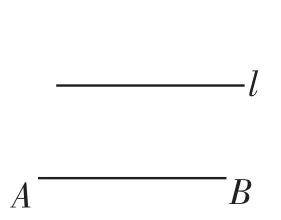
图1

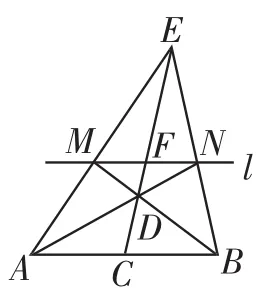
图2

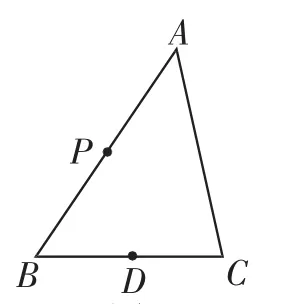
图3

2.推理验证

利用图形相似的知识，我们可以推理验证AC=CB.

（1）若线段a、b、c、d的长度均不为0，则下列比例式中，一定可以得出b=d的是（）.

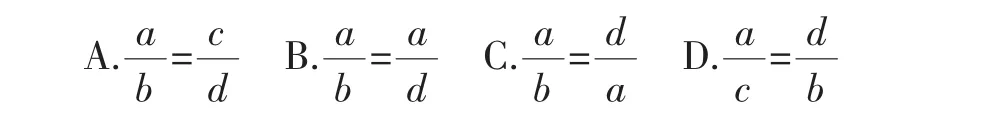
（2）由MN∥AB，可以推出△EFN∽△ECB，△EMN∽△EAB，△MND∽△BAD，△FND∽△CAD.所以有，所以AC=CB.

3.拓展研究

如图3，△ABC中，D是BC的中点，点P在AB上.

（3）在图3中只用直尺过点P作直线l∥BC.（写出画法，作出图形，保留作图痕迹）

（4）依据（3）中直线l的画法，求证：l∥BC.

解：（1）选B.

（3）分别连接CP、AD相交于点E，连接BE并延长交AC于点Q，过点P、Q作直线l，则直线l即为所求.

下面展示参考答案关于（4）的解法，通过作平行线构造相似三角形，进而转化比例线段，再证相似得角相等，证平行.

（4）证明：如图4，过点E作MN∥BC，分别交AB、AC于点M、N.

因为MN∥BC，所以△AME∽△ABD，△AEN∽△ADC，所以=

图4

因为点D是BC的中点，所以BD=CD，所以ME=EN.

因为MN∥BC，所以△PME∽△PBC，△QEN∽△QBC，所以，所以.又因为∠PEQ=∠CEB，所以△PEQ∽△CEB，所以∠QPE=∠BCE，所以PQ∥BC，即l∥BC.

二、解法探究

上述（4）的解法是第二问预设解法的逆向思考，但是这种解法用到的图形比较复杂，需要证明多组三角形相似，涉及比例线段较多，同时对转化、替换方面要求较高，只要有某处处理不到位，解答便会陷入“死局”，有没有思路、方法比较自然的解法呢？笔者进行了如下探究.

思路1：倍长中线.

探究1：根据题目的条件特征“点D为BC的中点”，可以倍长中线，这是比较自然的想法.

证法1：如图5，延长ED到点E′，使E′D=ED.

因为BD=CD，所以四边形BECE′为平行四边形，所以PE∥BE′，所以△APE∽△ABE′，所以

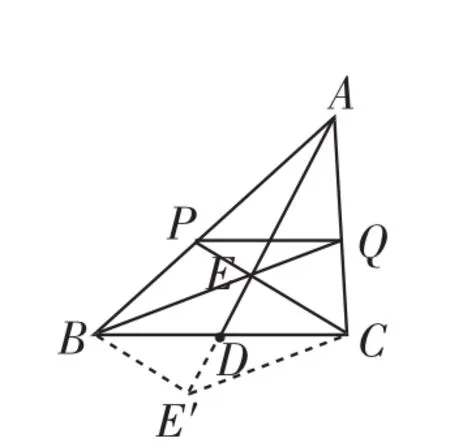
图5

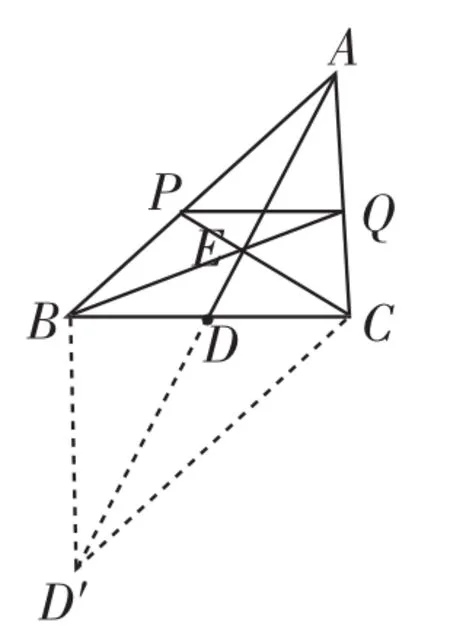
图6

探究2：既然可以倍长△BCE的中线ED，是否可以尝试倍长△ABC的中线AD呢？

证法2：如图6，延长AD到点D′，使DD′=AD.

因为BD=CD，所以四边形ABD′C为平行四边形，所以AB=CD′，AC=D′B.因为AP∥CD′，所以△APE∽△D′CE，所以

思路2：构造中位线.

探究3：根据题目的条件特征“点D为BC的中点”，也可以构造三角形的中位线，这也是常见的辅助线之一.

证法3：如图7，分别取BQ、CP的中点M、N，连接DM、DN.

因为D为BC的中点，所以BP=2DN，CQ=2DM.

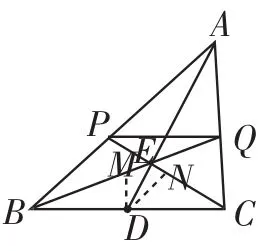
图7

探究4：证法3是在△ABC内部构造中位线，那么是否可以尝试向△ABC外构造中位线？

证法4：如图8，作BG∥AD，交CP的延长线于点G，作CH∥AD，交BQ的延长线于点H.

易得DE是△BCG和△BCH的中位线，则BG=2DE=CH.

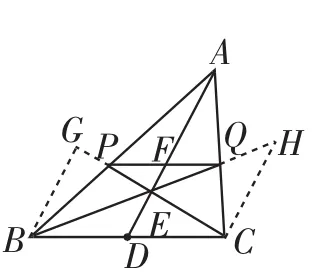
图8

思路3：面积法.

探究5：张景中院士曾言：“三角形中所有的线段比例问题都可以转化为面积问题来解决”，根据图形特征，点D是BC边的中点，可得S△ABD=S△ACD，S△BED=S△CED，所以S△AEB=S△AEC.因此也可尝试利用面积法为两个比例式搭建中间桥梁，来证明比例式相等，从而解决该问题.

证法5：如图9，作BF⊥CP，AG⊥CP，CH⊥BQ，AI⊥BQ，垂足分别为点F、G、H、I.

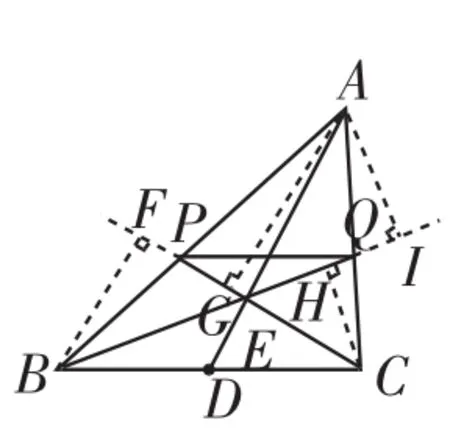
图9

因为BD=CD，所以S△ABD=S△ACD，S△BED=S△CED，所以S△AEB=S△AEC，所以.又因为∠PAQ=∠BAC，所以△PAQ∽△BAC，所以∠APQ= ∠ABC，所以PQ∥BC.

思路4：间接证法.

探究6：根据题目的结论特征，是要证两条直线互相平行，而在同一平面内两条直线的位置关系就是两种，即相交或平行，因此当直接证平行较困难时，可以考虑证明两条直线不相交，正难则反，这是解决数学问题一种重要的策略，反证法就是这种策略之一.

证法6：如图10，假设PQ不平行BC，则过点P作l′∥BC，交AC于点E′，连接BE′交CP于点O′，连接AO′并延长交BC于点D′.

由（2）可得：D′为BC的中点.而点D 为BC的中点，这与“一条线段有且只有一个中点”矛盾，所以假设不成立，所以PQ∥BC.

探究7：证法6是用反证法来解决的一种间接证明方法，在初中范围内还学习过一种间接证明的方法，那就是“同一法”，能否用“同一法”来解决呢？

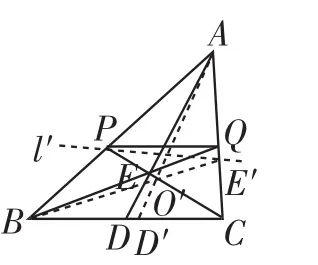
图10

证法7：如图11，作PF∥BC，交AC于点F，连接BF交PC于G，连接AG并延长交BC于点D′.

由（2）可得D′为BC的中点.又因为D为BC的中点，所以D、D′重合，所以AD 和AD′为同一条直线，所以G、E为同一点，所以BG、BE为同一条直线，所以F、Q为同一点，所以PQ与PF为同一条直线.又因为PF∥BC，所以PQ∥BC.

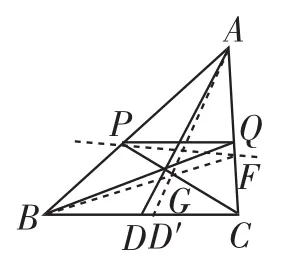
图11

三、拓展与思考

1.利用“塞瓦定理”解决（4）

塞瓦定理：如图12，设P、Q、R分别是△ABC的边BC、CA、AB上的点，则AP、BQ、CR三线共点的充要条件是

图12

下面我们可以利用塞瓦定理简洁解决（4）.简证：如图13，由塞瓦定理得：=1.又BD=DC，则=，则PQ∥BC.

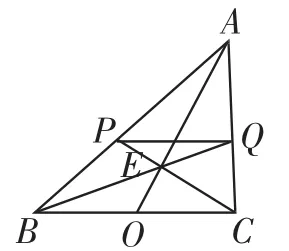
图13

2.问题（4）的变式探究

如图14，若点D不是BC的中点，而是BC的靠近点B的n等分点（n＞2，n为整数），即，显然此时PQ不再平行BC，那么会有其他什么发现呢？

笔者尝试利用BD和BC来表示BG，在求出BG的同时，得到了一个简洁的比例式：=n-2.

证明：如图14，过点Q作FQ∥BC，设AQ=a，QC=b.

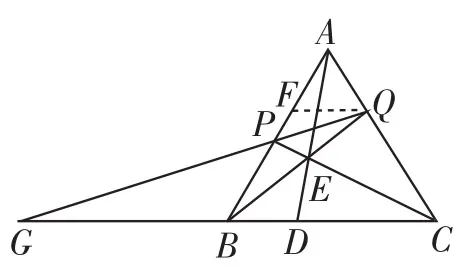
图14

设AP=（n-1）ak，PB=bk.

3.结论的应用

由本题我们可以发现：“用无刻度的直尺可以作出两条平行线段中任一条线段的中点”，这为我们利用尺规作图提供了新的模型.

问题：仅用直尺如何作出矩形的对称轴？

作法：如图15，连接对角线AC、BD相交于点I，再根据该模型作出BC边的中点H，则过点I、H的直线l即为矩形ABCD的一条对称轴，同样可以画出另一条对称轴.

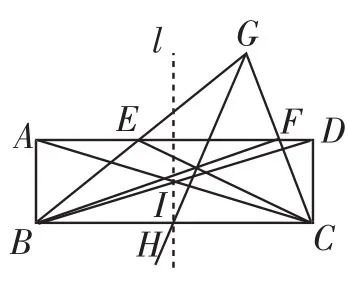
图15

四、写在最后

从以上解法探究可以发现，我们在解综合题时，要善于抓住题目中的条件特征、结论特征和图形特征，从中寻找突破口，联想所学知识和方法，唤醒过程经验，经历理性分析，利用基本模型，循序渐进地打开解题思路之门，最终促进学生解法的自然生成.在素质教育和创新教育的今天，作为肩负着数学教育任务的教师，我们与数学为伴，数学离不开解题，谁也无法教会我们解答所有的题目，重要的是，通过有限道题的学习去领悟那种解无限道题的数学机智，那么，怎样才能“通过有限道题的学习去领悟那种解无限道题的数学机智”呢［1］？笔者的体会是抓住题目的特征，进行自觉地解题分析，正如波利亚在《怎样解题》一书中（P15）指出的：“一个好的教师应该懂得并且传授给学生下述看法：没有任何问题是可以解决得十全十美的，总剩下些工作要做.经过充分的探讨与钻研，我们能够改进这个解答，而且在任何情况下，我们总能提高自己对这个解答的理解水平.”唯此，才能增强我们的数学解题能力，优化认知结构，提高思维素质，才能创新教育思路，享受智慧人生.

参考文献：

1.罗增儒.中学数学解题的理论与实践［M］.南宁：广西教育出版社，2008.