聚焦中考二次函数压轴题的定值“情结”

☉安徽省南陵县春谷中学　邹守文



聚焦中考二次函数压轴题的定值“情结”

☉安徽省南陵县春谷中学邹守文

二次函数中考压轴题由于综合性强，难度大，对很多学生来说往往起到区分的作用，常常望而生畏，尤其是一类定值问题的证明，使得学生望而却步，本文对此作一总结，以期对学生的复习备考有所帮助.

一、长度定值

例1（2013年湖北荆门卷）如图1，已知关于x的二次函数y=x2-2mx+m2+m的图像与关于x的一次函数y=kx+1的图像交于两点A（x1，y1）、B（x2，y2）（x1＜x2）.

（1）当k=1，m=0、1时，求AB的长；

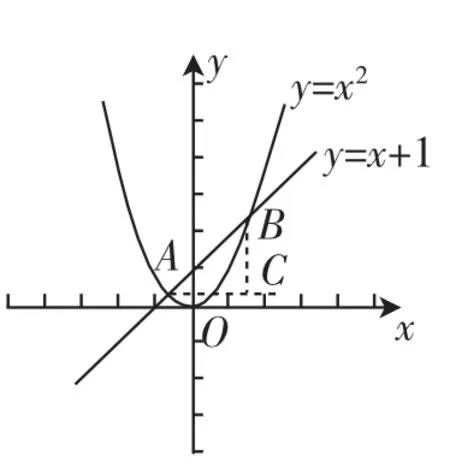
图1

（2）当k=1，m为任何值时，猜想AB的长是否不变？并证明你的猜想.

（3）当m=0，无论k为何值时，猜想△AOB的形状，并证明你的猜想.

（2）猜想：当k=1，m为任何值时，AB的长不变，即AB=

（3）略.

点评：证明线段长度是定值需要通过一元二次方程的根与系数的关系进行相应的计算，确定长度的具体值，要注意两点之间距离公式的灵活运用.

二、角度定值

例2（2015年甘肃兰州卷）已知二次函数y=ax2的图像经过点（2，1）.

（1）求二次函数y=ax2的解析式.

（2）一次函数y=mx+4的图像与二次函数y=ax2的图像交于A（x1、y1）、B（x2、y2）两点.

（3）根据第（2）问，说出一条你能得到的结论.（不要求证明）

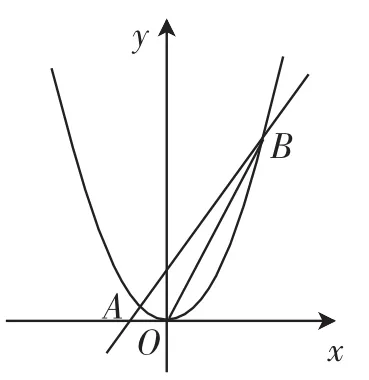
图2

图3

（2）①略.

②因为A（x1，y1）、B（x2，y2）是抛物线y=x2与直线y= mx+4的交点，联立得x1+x2=4m，x1x2=-16.

因为A（x1，y1）、B（x2，y2）在直线y=mx+4上，所以y1= mx1+4，y2=mx2+4，则y1-y2=m（x1-x2），所以AB2=（x1-x2）2+ m2（x1-x2）2=（1+m2）（x1-x2）2.

因为x1+x2=4m，x1x2=-16，所以（x1-x2）2=（x1+x2）2-4x1x2=（4m）2-4×（-16）=16m2+64，所以AB2=（x1-x2）2+（y1-y2）2=（1+m2）（16m2+64）=16（1+m2）（m2+4）.

则AO2+BO2=16（1+m2）（m2+4）=AB2，所以△AOB是直角三角形.

（3）无论m取什么值，△AOB都是直角三角形.

点评：（2）②的本质是∠AOB=90°，这是一个定值.判断角是否为定值，要通过计算角度的大小，一般可以利用勾股定理的逆定理或借助三角函数去确定角度的值为定值.

三、和定值

例3（2013年广西南宁卷）如图4，抛物线y=ax2+c（a≠0）经过C（2，0）、D（0，-1）两点，并与直线y= kx交于A、B两点，直线l过点E（0，-2）且平行于x轴，过A、B两点分别作直线l的垂线，垂足分别为M、N.

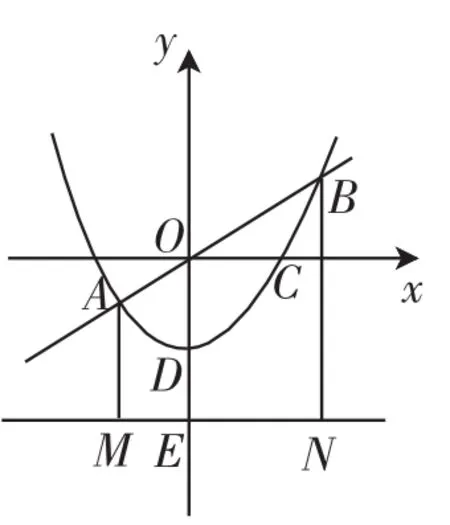
图4

（1）求此抛物线的解析式；

（2）求证：AO=AM；

（3）探究：

因为直线l过点E（0，-2）且平行于x轴，所以点M的纵坐标为-2，所以AM=m2+1，所以AO= AM.

点评：判断两条线段的和为定值，可以分别求出线段的长度，也可以利用相似三角形的性质、全等三角形的性质、三角形中位线定理、梯形中位线定理等，本题的核心是抛物线上任意一点到焦点的距离等于该点到准线的距离，这个结论非常重要，请同学们认真领会.

四、差定值

例4（2015河南卷）如图5，边长为8的正方形OABC的两边在坐标轴上，以点C为顶点的抛物线经过点A，P是抛物线上点A、C间的一个动点（含端点），过点P作PF⊥BC于点F，点D、E的坐标分别为（0，6）、（-4，0），连接PD，PE，DE.

（1）请直接写出抛物线的解析式.

（2）小明探究点P的位置发现：当点P与点A或点C重合时，PD与PF的差为定值.进而猜想：对于任意一点P，PD与PF的差为定值.请你判断该猜想是否正确，并说明理由.

（3）小明进一步探究得出结论：若将“使△PDE的面积为整数”的点P记作“好点”，则存在多个“好点”，且使△PDE的周长最小的点P也是一个“好点”.请直接写出所有“好点”的个数，并求出△PDE周长最小时“好点”的坐标.

图5

图6

（3）好点共11个.

在点P运动时，DE的大小不变，所以PE与PD的和最小时，△PDE的周长最小.

因为PD-PF=2，所以PD=PF+2，所以PE+PD=PE+PF+ 2.

当P、E、F三点共线时，PE+PF最小，此时，点P、E的横坐标都为-4，将x=-4代入y=-x2+8中，解得y=6，所以P（-4，6），此时△PDE周长最小，且△PDE的面积为12，点P恰为“好点”.所以△PDE周长最小时点P的坐标为（-4，6）.△PDE的面积S=-（x+6）2+13.由于-8≤x≤0，可得4≤S≤13，所以S的整数值为10个.由图像可知，当S=12时，对应的“好点”有2个，所以“好点”共有11个.

点评：用代数式分别表示线段的长度，然后通过作差，进行适度运算获得定值，如本题设P点坐标为表示出PF的长度，构造PD所在的直角三角形，表示PD的长度，通过求差法得到PD-PF=2.

五、积定值

例5（2015年广西南宁卷）在平面直角坐标系中，已知A、B是抛物线y=ax2（a＞0）上两个不同的点，其中点A在第二象限，点B在第一象限.

（1）如图7所示，当直线AB与x轴平行，∠AOB=90°，且AB=2时，求此抛物线的解析式，以及A、B两点的横坐标的乘积.

（2）如图8所示，在（1）所求得的抛物线上，当直线AB与x轴不平行，∠AOB仍为90°时，A、B两点的横坐标的乘积是否为常数？如果是，请给予证明；如果不是，请说明理由.

（3）在（2）的条件下，若直线y=-2x-2分别交直线AB、y轴于点P、C，直线AB交y轴于点D，且∠BPC= ∠OCP，求点P的坐标.

图7

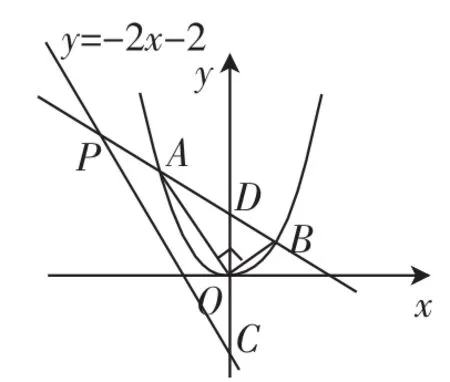
图8

简解：（1）A、B两点的横坐标的乘积为xAxB=-1.（过程略）

（2）xAxB=-1为常数.

如图9，过点A作AM⊥x轴于点M，过点B作BN⊥x轴于点N，所以∠AMO=∠BNO=90°.

所以∠MAO +∠AOM = ∠AOM+∠BON=90°.

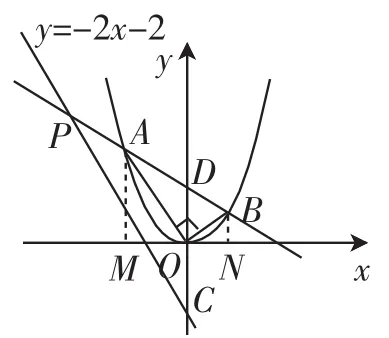
图9

设A（xA，yA），B（xB，yB），因为A（xA，yA）、B（xB，yB）在y= x2图像上，所以yA=xA2，yB=xB2，所以-xAxB=yAyB=xA2xB2，所以xAxB=-1为常数.

点评：第（1）问是第（2）问的铺垫，题目采用了从特殊到一般的命题思路，相似三角形的运用是问题获得解决的保障.

六、比定值

例6（2014年江苏苏州卷）如图10，二次函数y= a（x2-2mx-3m2）（其中a，m是常数，且a＞0，m＞0）的图像与x轴分别交于点A、B（点A位于点B的左侧），与y轴交于C（0，-3），点D在二次函数的图像上，CD∥AB，连接AD，过点A作射线AE交二次函数的图像于点E，AB平分∠DAE.

（1）用含m的代数式表示a；

（3）设该二次函数图像的顶点为F，探索：在x轴的负半轴上是否存在点G，连接GF，以线段GF、AD、AE的长度为三边长的三角形是直角三角形？如果存在，只要找出一个满足要求的点G即可，并用含m的代数式表示该点的横坐标；如果不存在，请说明理由.

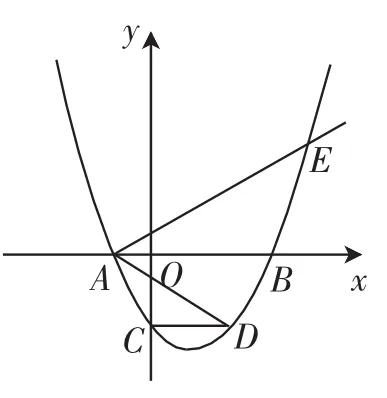
图10

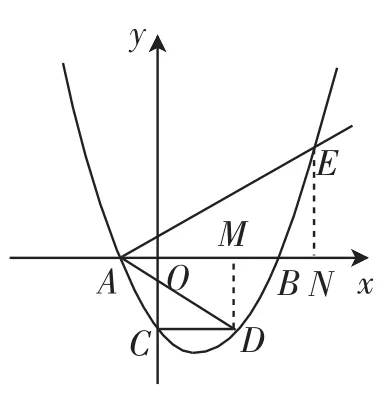
图11

（2）如图11，过点D、E分别作x轴的垂线，垂足为M、N.

由a（x2-2mx-3m2）=0，解得x1=-m，x2=3m，则A（-m，0），B（3m，0）.

因为CD∥AB，所以点D的坐标为（2m，-3）.

因为AB平分∠DAE，所以∠DAM=∠EAN.

因为∠DMA=∠ENA=90°，所以△ADM∽△AEN，所以

因为AM=AO+OM=m+2m=3m，AN=AO+ON=m+4m= 5m，所以，即为定值.

（3）以线段GF、AD、AE的长度为三边长的三角形是直角三角形，此时G点的横坐标为-3m.

七、三角函数定值

例7（2015年湖北十堰卷）抛物线C1：y=ax2+bx+（a≠0）经过点A（-1，0）和B（3，0）.

（1）求抛物线C1的解析式，并写出其顶点C的坐标.

（2）如图12，把抛物线C1沿直线AC方向平移到某处时得到抛物线C2，此时点A、C分别平移到点D、E处.设点F在抛物线C1上且在x轴下方，若△DEF是以EF为底的等腰直角三角形，求点F的坐标.

（3）如图13，在（2）的条件下，设点M是线段BC上一动点，EN⊥EM交直线BF于点N，P为线段MN的中点.当点M从点B向点C运动时：

①tan∠ENM的值如何变化？请说明理由；

②点M到达点C时，直接写出点P经过的路线长.

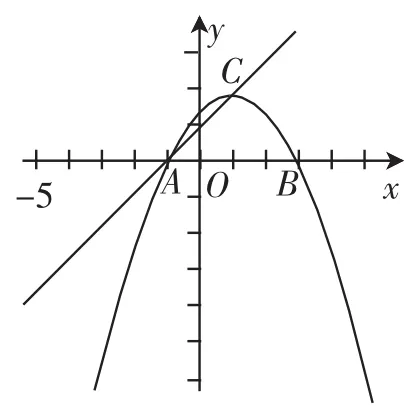
图12

图13

简解：（1）抛物线C1的解析式为y=-顶点C的坐标为（1，2）.（过程略）

（2）F（-3，-6）.（过程略）

图14

点评：第（3）问先证明Rt△NGE∽Rt△ECM，从而得出，所以tan∠ENM=，由EC、NG是定值可得tan∠ENM为定值.

八、三角函数差定值

例8（2013年湖南株洲卷）已知抛物线C1的顶点为P（1，0），且过点将抛物线C1向下平移h个单位（h＞0）得到抛物线C2.一条平行于x轴的直线与两条抛物线交于A、B、C、D四点（如图15），且点A、C关于y轴对称，直线AB与x轴的距离是m2（m＞0）.

（1）求抛物线C1的解析式的一般形式；

（2）当m=2时，求h的值；

（3）若抛物线C1的对称轴与直线AB交于点E，与抛物线C2交于点F.求证：tan∠EDF-tan∠ECP=

图15

（2）h=5.（过程略）

（3）因为直线AB与x轴的距离是m2，所以点B、C的纵坐标为m2.

又因为抛物线C1的对称轴为直线x=1，所以CE=1+ 2m-1=2m.

因为点A、C关于y轴对称，所以点A的坐标为（-1-2m，m2）.

所以AE=ED=1-（-1-2m）=2+2m.

设抛物线C2的解析式为y=2m-1）2-h=m2，解得h=2m+1.

所以EF=h+m2=m2+2m+1.

点评：第（3）问用m表示出相应的线段是解题的关键，也是本题的难点.

九、面积定值

例9（2011年广东广州卷）已知关于x的二次函数y=ax2+bx+c（a＞0）的图像经过点C（0，1），且与x轴交于不同的两点A、B，点A的坐标是（1，0）.

（1）求c的值；

（2）求a的取值范围；

（3）该二次函数的图像与直线y=1交于C、D两点，设A、B、C、D四点构成的四边形的对角线相交于点P，记△PCD的面积为S1，△PAB的面积为S2，当0＜a＜1时，求证：S1-S2为常数，并求出该常数.

简解：（1）c=1.（过程略）

（2）a＞0且a≠1.（过程略）

所以S1-S2=S△CDA-S△ABC=

所以S1-S2为常数，该常数为1.

点评：分别求出三角形的面积，再作差，得到结论.