基于问题导向的“二次函数章复习”课例及分析

☉江苏省南通市通州区实验中学　潘红裕



基于问题导向的“二次函数章复习”课例及分析

☉江苏省南通市通州区实验中学潘红裕

数学复习课一直是初中数学教学的重要组成部分，特别是在初三后期的教学显得尤为重要.一堂优质高效的数学复习课，不仅能帮助学生回顾和应用所学知识，还能使学生深化对数学知识的理解，更能够使学生对数学方法的总结与提炼、数学思维能力的提升、数学思想的升华起到促进作用.而目前一般复习课采用的主线都是先让学生回顾基础知识或者做几道简单的题目，然后教师再选择几道例题和学生一起进行分析，最后找几道难题或历届中考题进行巩固练习.这种流水线式的固化模式，很难激发出学生的学习兴趣，更谈不上培养学生发现问题、分析问题、解决问题的能力.那如何提高数学复习课的有效性，再次激发学生学习的积极性？在区2016届初三数学教师上岗培训暨初三期中质量分析活动中，受教研员的邀请执教了一堂“二次函数章复习课”，笔者尝试以问题驱动带动知识点、方法的生成，取得了较好的教学效果.本文整理了该课的教学设计，并整体阐述教学立意，与同行研讨.

一、“二次函数章复习”教学设计

（一）教学目标

（1）了解二次函数的意义，会选取适当的方法求二次函数的解析式，巩固二次函数基础知识与技能；

（2）掌握利用函数的观点看一元二次方程，进一步体会数形结合、转化等数学思想；

（3）在二次函数综合题的求解及反思中，提高分析问题和解决问题的能力.

（二）教学重、难点

重点：用函数的观点看一元二次方程及二次函数的综合运用；

难点：二次函数综合运用.

（三）教学过程

1.开课引入

师：同学们，到目前为止我们已经学习了哪几种函数类型？设计意图：从总体上把握初中阶段所学的函数版块.生：正比例函数，一次函数，二次函数.

师：函数知识是初中数学的重要内容之一，函数思想更是贯穿于初高中数学的始终，尤其是二次函数更是连接初、高中数学的桥梁.近几年二次函数一直是南通中考命题的热点和难点内容.所以学好本章知识尤为重要，相信大家通过这堂课的复习，一定会对本章知识乃至函数知识的理解和运用会更加深刻！

2.合作探究

问题1：观察如图1所示的抛物线y=ax2+bx+c，你能根据图像得出哪些信息？

图1

设计意图：通过学生观察函数图像，回顾二次函数图像的开口方向、对称轴、顶点坐标、x轴交点的情况等与a，b，c的关系，进一步理清函数图像的性质.

问题2：若抛物线经过点A（-1，0），B（2，0），你又能得出哪些结论呢？

师：（追问）这是利用图像的什么性质？

设计意图：回顾二次函数的对称性.

问题3：若抛物线经过点A（-1，0），B（2，0），C（0，1），你还可以求出什么？

生：二次函数的解析式.

师：（追问）可以用哪几种方法？

设计意图：通过一个问题把求二次函数解析式的三种不同方法进行了系统复习.

问题4：若抛物线y=ax2+bx+c经过点A（-1，0），B（2，0），C（0，1），根据图像解决下列问题：

①方程ax2+bx+c=0的解是______；方程ax2+bx+c=1的解是_______；

②若方程ax2+bx+c=k有实数根，则k的范围是_______；

③不等式ax2+bx+c＜1的解集是________.

师：（追问）我们已经知道二次函数的一般式和一元二次方程非常类似，那么你能通过二次函数的图像来求下面方程的解吗？你能用类似的方法来求下面不等式的解集吗？

设计意图：通过几个问题的追问，让学生能利用数形结合的思想来求一元二次方程的解，然后类比其相同的方法求一元二次不等式的解集，相当于把一元二次不等式转化成求函数值小于1时自变量的范围，从而利用图像找函数值小于1的部分写出自变量的范围，就是不等式的解集，再次渗透函数中重要的数形结合思想.

问题5：若抛物线经过点A（-1，0），B（2，0），C（0，1），通过对以上函数知识的复习和回顾，请同学们结合此函数图像，以小组合作的形式设计一个问题，并解答.

学生部分成果展示：①求△ABC的面积.②在抛物线BC上是否存在一点D，使得四边形ACDB的面积最大.③求出该抛物线关于x轴和y轴对称抛物线的解析式.④在抛物线上是否存在一点D，使得以A、B、C、D为顶点的四边形为平行四边形.

设计意图：通过让学生自己编题并解答，把与其相关知识有机地融合在一起，即巩固了本章的基础知识，又能让学生更加灵活地解决二次函数的综合性问题.

3.拓展提高

例题如图2，若点E（1，1）是该抛物线上的一个定点，点D是x轴上的一个动点，以点D为直角顶点作等腰Rt△EDF（E、D、F按顺时针方向排列），当点F在抛物线上时，求OD的长.

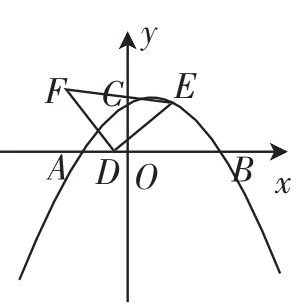
图2

设计意图：以熟悉的图形为背景，加上点的运动，综合考查学生在动态背景下处理图形的应用能力，能较好地培养学生掌握数形结合的思想、运动变化的思想、分类讨论的思想，也为学生较好地掌握几何基本图形打下基础.

4.课堂小结

师：谈谈对本堂课学习后的收获.

设计意图：本堂课自始至终围绕着同一条抛物线展开，以这条抛物线为主线复习了二次函数的图像和性质、待定系数法求抛物线的解析式、二次函数和一元二次方程的关系、如何借助图像求一元二次不等式的解集，在这里向学生处处渗透数形结合的思想.最后通过拓展提高题的解析让学生初步掌握如何分析动点类型的二次函数综合题，

5.课后作业

完成拓展应用中（E、D、F按逆时针方向排列）“当点F在抛物线上时，求OD的长”.

设计意图：进一步巩固拓展提高题，让学生加深对此类问题的理解.

二、教学立意的进一步阐述

函数知识是初中数学的重要内容之一，函数思想更是贯穿于初高中数学的始终，尤其是二次函数在初中函数教学中的重要地位，它不仅是初中代数内容的引申，也是初中数学教学的重点和难点之一，更是连接初、高中数学的桥梁.近几年二次函数一直是南通中考的热点、难点内容.鉴于初三学生在新课的学习中已掌握二次函数的定义、图像及性质等基本知识，而且刚刚经过期中考试复习，学生应该对本章的基础知识和方法还是比较熟悉的，所以笔者想通过这堂课的复习，在解题方法和数学思想这两方面能够对学生有所帮助.

（1）借助抛物线的图像回顾二次函数的性质向学生渗透数形结合的数学思想，对学生基本数学思想和素养的形成起到推动作用.主要体现在问题1，2，3中，借助于同一个图形设置不同的问题，避免学生再花时间重新认识图形，提高了学生课堂学习的效率，也能激发学生学习的兴趣，提高了课堂的容量.

（2）回顾二次函数与一元二次方程知识的联系，能利用图像解决简单的一元二次不等式的解集问题，为学生的后续发展提供动力.因为我们知道已知二次函数值的范围求自变量的范围其实就是解一元二次方程，在复习课中能向学生渗透一点，或者说能适当的拓展一些，能为学生以后的高中学习提供一点帮助，一些联系，符合学习的可持续发展原则.

（3）通过开放性问题的设置，有利于培养学生的自主探究、合作交流能力；有利于加深对重点知识、重点方法的理解；有利于培养学生的创新思维，提高学生的创新能力；有利于提高学生分析问题、解决问题的能力.所以教师应在复习课中更能深入地钻研教材，联系生活实际，挖掘一些封闭题中的开放性元素，设计恰当的开放性问题，使学生的思维得到发展，提高复习课的有效性.

（4）由于复习课并不是教材上所规定的内容，对复习课的整体构思，优选内容就显得尤为重要，我们不能把复习课简单地看作知识点的复习和习题的训练，而是要让一部分优秀的学生能得到更高层次的发展，所以在本节课的设计中借助于拓展题来提高学生分析和解决综合题的能力.因为近几年南通中考的压轴题一直以二次函数为背景来命题的，而且动点类问题也一直是中考的热点内容，所以在命制这道题时把点的运动、直角型基本图形、分类讨论数学思想有机地融合在一起，能促进优秀学生深入思考、挑战高分.