老树发新枝 别样的精彩——对一节“二次函数的应用”复习课的思考

☉浙江省衢州市实验学校　詹金芳☉浙江省宁波滨海国际学校　胡赵云



老树发新枝别样的精彩——对一节“二次函数的应用”复习课的思考

☉浙江省衢州市实验学校詹金芳
☉浙江省宁波滨海国际学校胡赵云

这是一节“浙派”名师班学员关于二次函数应用的复习教学研讨课，授课教师利用一个熟悉的情境，构设了一组巧妙的问题，演绎出一节高水平的思维活动课，现将课堂实录与笔者的思考整理成文，以供同行参考.

一、课堂实录

1.情境引入

课堂一开始，教师给出了一道学生十分熟悉的篱笆围鸡场问题.

引例用长为60米的篱笆围成一个矩形养鸡场，怎样围才能使得养鸡场的面积最大，最大面积是多少？

在学生独立完成的基础上，教师请学生分享解答.

生1：设矩形养鸡场的长为x米，则其宽为（30-x）米.

矩形的面积S=x（30-x）=-（x-15）2+225（0＜x＜30）.

所以当x=15时，矩形面积最大，最大面积为225平方米.

老师追问：取值范围是怎么得到的？

生1：因为矩形的长和宽都要大于0，所以得到x的范围0＜x＜30.

教师将学生的过程进行板书，并追问还有其他方法吗？

生2（脱口而出）：周长一定的矩形中，正方形面积最大，所以边长为15时，面积最大.

教师将这一结论书写在黑板上，并追问：你是怎么知道这个结论的？

生2（补充）：小学老师讲过的.

教师追问：同学们能说明这个结论的正确性吗？

师生一起着手验证结论：先通过特殊情况来尝试验证，如引例中周长为60的矩形，边长为15时面积最大，此时正好是一个正方形，可是这不能代表一般情况，因此，我们需要从特殊走向一般，即用字母m来表示周长，能否证明当矩形边长为时，其面积达到最大？

教师总结并板书：当我们碰到一个实际问题时，要学会用数学模型（如函数、方程等）来解决；在解决问题的过程中我们发现了一个重要结论：周长一定的矩形中，正方形面积最大.用图示进一步说明（如图1）.

图1

2.变式拓展

源问题：空地上有一面长为32米的残墙，利用残墙和长为60米的篱笆围成一个矩形养鸡场，怎样围才能使得养鸡场的面积最大，最大面积是多少？

问题给出三分钟左右，大部分学生已完成了解答.

图2

由二次函数性质可知，当x=30时，最大面积S=450.

全班同学基本上能算出这个答案，而后教师马上变换条件，给出了变式问题.

变式拓展：空地上有一面长为12米的残墙，利用残墙和长为60米的篱笆围成一个矩形养鸡场，怎样围才能使得养鸡场的面积最大，最大面积是多少？

问题一给出，有部分学生开始嘀咕：这个问题不就是二次函数根据自变量取值范围求最值嘛.不一会儿大部分同学举起手来示意完成了解答，部分成绩好的同学甚至不屑动笔去算.

生5：老师这问题不难，和前面一样，设矩形的长为x，则其宽为30-，同样可得矩形的面积S=x（x-30）2+450，因考虑到实际，自变量的取值范围是0＜x≤12，所以根据二次函数的性质可知，当x=12时，S的最大值为288.

不等生5讲完，生6迫不及待地站起来说：“这个问题和源问题一样，当篱笆长度保持60米不变时，只要对墙长a进行分类讨论就行了.若a＜30，则当x=a时，S取得最大值，最大值S=-a2+30a；若a≥30，则当x=30时，S取得最大值，最大值S=450.”生6在讲解的同时一边在黑板画出了二次函数图像的草图（图3），并示意其他学生如何根据自变量的范围确定函数的最值.

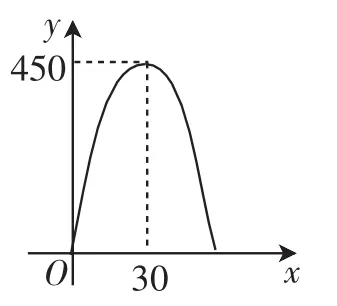
图3

教师对两位学生的分析和解答给予了充分的肯定，并再次明晰遇到二次函数求最值时，要学会借助函数图像进行直观的分析，再代入解析式进行精确的求解.同时，教师不紧不慢地追出一问：“同学们，墙长为12米时，围成的矩形最大面积真的是288平方米吗？”

这一问，打破了教室原有的热闹氛围，一个个目瞪口呆，你看看我，我看看你，一脸茫然，似乎被这个问题问得莫名其妙，一时间，教室里彻底安静了下来.

3.探究升华

许久，教师再问：你们是如何理解“利用残墙和篱笆围矩形”的，这和我们以前接触过的“以残墙为矩形的一边”有区别吗？

经教师这样一引导，教室里像炸开了锅似得，同学们各种神情的都有，纷纷向同伴去征求意见和想法，几分钟后，全班绝大多数同学开始将目光投向几个成绩比较突出的同学身上.不多时，教室里传来“有了”“有了”的声音，而后，教室的人群纷纷向发出高分贝声音的地方集聚.

生7：按照图2的围法，最大面积是288，但是如果按照图4的围法，将残墙视为矩形一边的一部分（学生边讲解边画图），结果就不是288了.并写出了如下解答过程.

图4

生7：设BE=x，则AE=12+x，AC=24-x.

所以S=（12+x）（24-x）=-（x-6）2+324.

因此，当x=6时，所围矩形面积最大，最大面积为324平方米.

生7的发言赢得了全班同学热烈的掌声.

教师在肯定了生7的基础上又追出一问：“假如残墙为a米，其余条件不变，那么所围的矩形最大面积又为多少？”

问题抛出后，学生纷纷尝试解决，部分同学又开始嘀咕起来：“不就和前面一样进行分类讨论吗？”说着说着，发现不对劲了.“好像有点问题，a的取值范围很难界定……”

此时，部分成绩比较优秀的同学纷纷开始了解答.几分钟后，同学们开始了讨论，老师巡视过程中发现部分学生有想法和困惑，于是请学生发言.

生9的发言可以说震惊了全班同学乃至后场听课的老师，听课老师情不自禁地鼓起了掌声，进而全班响起了热烈的掌声.

老师表扬生9的发言，能用我们课堂一开始所获得的结论解决该问题，具有极强的观察能力和应用能力.随后老师又抛出一个问题：那么，当a＞20时，结果又会如何呢？

仍有部分学生不以为然，认为剩下的不过是简单问题，不屑一做，结果一动手就发现，这可是一个棘手的问题，于是教室又一次进入安静的氛围中.

生10：当a＞20时，我们需分两种情况讨论.当20＜a＜30时，经过对两种围法的比较可以发现，按照图2的方式围成正方形（墙有多余）的面积要大，所以最大面积S=a2+30a平方米；当a≥30时，最大面积就是450平方米.

老师在生10叙述的同时，与全班学生一道进行了计算推理，形成了共识.

（1）当0≤a≤20时，按照图4的方式围，能得到最大面积S=

（2）当20＜a＜30时，按照图2的方式围，能得到最大面积S=-a2+30a；

（3）当a≥30时，按照图1的方式围，能得到最大面积S=450.

4.课堂小结

本节课，我们通过一个熟悉的围篱笆问题，应用了二次函数模型解决相关问题，梳理了二次函数的相关知识，在解决问题中获得了一个结论——周长一定的矩形中，正方形面积最大，并应用这一结论解决了围篱笆问题中平时被我们疏忽的问题.在日常生活中，我们要善于用所学的数学知识解决实际问题，根据数学推理论证获得相关结论，并能应用相关结论和模型恰当地解决一些复杂的问题.

二、课后反思

1.老树发新枝，别样的精彩，值得提倡的教学研究取向

本节课教师利用一个师生十分熟悉的篱笆围鸡场的情境（多种版本教材都用于例习题设计的情境），通过对情境的深度挖掘，构设出一节精彩的高思维含量的数学课.

在用固定长度的篱笆和一面残墙围矩形养鸡场的背景中，老师们通常会沿着这样的思路进行问题设计：若在养鸡场中间隔一道栅栏，如图5，要使所围矩形的面积达到最大，应怎样设计方案，或者在养鸡场中间隔两道栅栏等.也有教师经常这样设计：在围养鸡场时要求开一道门，门的宽度为1米，如图6，如何设计方案才能使所围矩形的面积最大.让学生经历分析题中数量关系，构建二次函数模型，利用模型解决问题.这样的教学设计，与源问题相比，只是增加数量关系上的复杂性，从本质而言，它与源问题是同一层次的问题，没有在思维上作进一步的提升.这样的变式训练只是增加了学生解题的熟练程度，对学生思维能力的培养没有太大的帮助.

本节的教学，教师从最基本的问题出发，引导学生对问题进行深度挖掘，培养学生思维的发散性和深刻性.当残墙从32米变为12米时，问题已经发生了本质的变化，即由原来的残墙作为矩形养鸡场的一边变成以残墙作为矩形一边的部分，它带给学生思维上的冲击是巨大的，对于新问题中所呈现的数量关系的分析也是递进式的，它打破了学生原有的思维状态，给学生以全新的感受.在此基础上，教师对墙长进行一般化处理，当残墙为a米时，结果会如何.这又是一个新的挑战，多数学生难以对a的取值范围进行分类讨论，这是一个难点，从而将学生的思维引向深刻.这样的教学设计，从一个熟悉的情境出发，将问题进行变式，引导学生多维度思考问题，进而对问题进行一般化处理，在每一个环节中不断提升学生的思维水平，发展学生的能力，这样的设计是高效的，这样的教学研究值得提倡和推广.同时在本节课的教学中，教师进一步引导学生进行正确的审题，区分“以墙为一边”和“利用残墙”的区别和联系，对学生审题能力的培养也极为有利.

这种在“老树桩”上进行加工整理，让“老树”催生出“新枝”，让课堂迸发出新的气息，呈现出别样的精彩，它切实减轻了学生的负担，发展了学生的能力，培养了学生的思维，是我们教师教学研究的重要方向，值得我们学习和借鉴.

图5

图6

2.关注数学建模教学，构建“母子模型”是数学建模教学的探索方向

本节课始终围绕着利用二次函数模型解决实际问题展开教学，对二次函数的建模教学进行深度挖掘，重视模型的形成过程，抓住利用模型解决问题的关键——自变量的取值范围决定函数的最值.根据自变量的取值范围进行分类讨论，利用函数图像的直观性分析函数的最值问题，可以说本节课对于二次函数的建模教学成效显著.

本节课在落实二次函数建模教学过程中，再次构建新的数学模型，并用新的数学模型解决实际问题，使复杂的问题得到简单化的处理，是数学建模教学的重要研究方向.本节课通过用长度为60米的篱笆围成一个面积最大的矩形养鸡场，在对这个问题的研究中利用二次函数这一“母模型”进行分析，最终获得“在周长一定的矩形中，正方形的面积最大”的“子模型”（这一结论学生小学已经知道，但并不清楚其中的原理，用二次函数的知识进行分析，达到了知其然且知其所以然的目的）.而后在解决当残墙为12米时，如何围才能使得矩形的面积最大，学生再次利用“在周长一定的矩形中，正方形的面积最大”这一“子模型”解决新问题，使问题得到轻松解决；再此基础上，对问题进行一般化处理，学生又一次利用“子模型”进行分析研究，使复杂的数学问题变得简单易懂，使教学的难度得到有效的突破.

数学模型的价值在于它的一般化和普适性，人们可以借助数学模型分析实际问题，从而有效地解决问题.本节课教师充分引导学生构建“母子模型”，并用“母子模型”分析和解决复杂的实际问题，实现了化繁为简的目的.这是一节高水平的数学模型教学研究课，为我们在数学建模教学研究上提供了一条探索的方向.

3.注重数学思想的渗透，促进学生能力的提升

这是一节十分关注数学思想渗透的研究课，教师通过一个教学背景，适当变换条件，演绎出一节精彩纷呈的数学思维展示课，有效地促进了学生能力的提升.

本节课高度关注数学建模教学，将模型思想贯穿教学始终，并在二次函数建模过程中构建出新模型，将模型思想渗透于每一个环节，并为我们在数学建模教学上提供了一个值得探索的研究方向，将模型教学演绎得淋漓尽致.

教师在教学的过程中不断渗透一般化思想.教师通过具体的60米长的篱笆围成矩形养鸡场问题逐渐过渡到a米长的篱笆，经历由特殊走向一般的过程；在对残墙长度变更中经历由32米（非常特殊，体现残墙足够长的情境）变换到12米（墙长变小的情况下，将进行分类讨论），最后过渡到一般化的a米.让学生经历从具体的、特殊的数向抽象的、一般化字母的发展和过渡，这样的教学符合学生的认知规律，对学生能力的培养和思维的发展是有利的.

教学中，教师不断渗透数形结合和分类讨论思想.在利用二次函数模型解决实际问题时，教师不断引导学生结合函数图像分析和研究问题，从而更直观地发现函数的最值.在对残墙长度的研究中渗透分类讨论的数学思想，提供了分类的标准和依据，并从模型的角度有效地突破分类的难点.

这种时时渗透着数学思想，处处发展着数学能力的课堂教学，有效地促进学生思维的发展，是一节值得学习和推崇的教学研讨课.