几何新知教学：由特殊走向一般——以“13.1.2线段的垂直平分线的性质”为例

☉江苏省如皋市高新区实验初中　陈亚东



几何新知教学：由特殊走向一般——以“13.1.2线段的垂直平分线的性质”为例

☉江苏省如皋市高新区实验初中陈亚东

“特殊与一般”是初中数学几个最为重要的数学思想之一，它在学生获取几何知识过程中的作用是非常明显的.在几何教学中，学生可以从图形的特殊位置或图形（线段、角等）的特殊取值出发，通过对多种不同特殊情形下结论的探究，从而不完全地归纳出可能具有一般意义的数学结论，在经过“严格论证”后，这些结论将会被应用到今后的数学学习和问题解决之中.显而易见，特殊到一般是初中几何结论生成的重要通道，我们在教学中应高度重视.现呈现一则这样的教学案例，并谈一些体会，希望能给您带来启示.

一、教学片断及分析

1.教学内容

人教版八年级上册第十三章“13.1.2线段的垂直平分线的性质”.

2.背景分析

下面展示的是“轴对称”这一单元的第2课时的教学片断，前一单元中学生学习的“全等三角形”的性质与判定和本单元第1课时学习的“成轴对称的两个图形”的性质、线段的垂直平分线的概念等知识，为本节课的探究夯实了基础.这节课将要深入探讨的是线段的垂直平分线的性质和判定方法，它是学生进一步学习其他几何知识（等腰三角形、矩形、菱形、圆等）的基础，在学生的初中几何学习中作用巨大.所以教师在进行下面的片断教学前，已经带领学生梳理了前面获得的知识，并对本节课在几何学习中的地位进行了简单的陈述.

3.片断展示

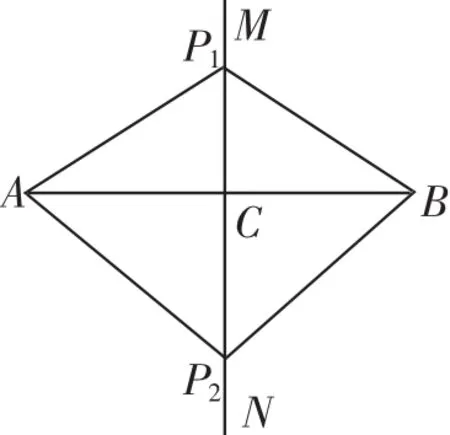
师：如图1，直线MN是线段AB的垂直平分线，C为垂足.你能得出哪些结论？

生1：A、B两点关于直线MN对称.生2：根据垂直平分线的定义，我可以得到∠ACN=∠ACM=∠BCM=∠BCN=90°，AC=BC=AB.

师：线段AC表示的是哪两个点之间的距离？

生3：点C与点A之间的距离.

师：BC呢？

生4：点C与点B之间的距离.

师：它们相等吗？

生（齐）：相等.

师：是不是在这条垂直平分线上的点到线段两个端点A、B的距离都相等呢？（教师稍作停顿，让学生思考片刻）现在，我们在MN再上取一点P1，请大家分别去量一量P1到点A与点B的距离，看看它们之间有怎样的关系.

学生活动：作图，并度量P1到点A、点B的距离.

2分钟后，学生活动结束.

师：相等吗？

生（齐）：相等.

师：如果在MN上再取一个点P2（教师在图1中标上点P2，连接P2A、P2B），P2到点A和点B的距离还相等吗？

生5：相等.

师：为什么呢？能用最近学过的知识来说明吗？

生6：A、B两点关于直线MN对称.所以如果将线段AB沿直线MN对折，线段P1A与P1B、线段P2A与P2B都是重合的，因此它们也分别相等.

师：根据轴对称的性质可以简单地给出一些理由，那么有没有更加严谨的证明方法呢？

生7：可以用全等来证明，如图1，根据“直线MN是线段AB的垂直平分线”，可以得到∠ACN=∠BCN=90°，AC=BC.又P2C=P2C，所以△P2CA≌△P2CB.所以P2A=P2B.

师：非常棒！看来全等三角形还真是个解决问题的好工具呢！那么，如果我们在MN上取点P3、P4、…（教师在图1中标上点P3、P4，…），它们到点A和点B的距离还分别相等吗？

生8：相等.因为MN两侧对称的两个三角形依然全等.

师：好的.看来，不只是线段AB的中点到线段两个端点的距离相等哦！

生（齐）：对！

师：但我们要感谢“线段AB的中点”，从这个特殊位置出发，我们发现了一个对今后几何学习有重要影响的定理.你能用一句话概括一下刚刚发现的这个结论吗？

生9：线段垂直平分线上的点与这条线段两个端点的距离相等.

师：非常棒！这样我们就得出了线段的垂直平分线的性质（板书）.

4.片断分析

线段的垂直平分线与线段的交点，是这条线段的中点，在线段和它的垂直平分线上，这个点是一个特殊点，是很多数学结论“诞生”的起点.教师引导学生从这个点开始，去猜想并验证“线段垂直平分线上的点与这条线段两个端点的距离相等”这一结论.学生有垂直平分线的概念，从这个特殊点上得出结论并不难.在学生知晓这个结论后，接下来就应是经历特殊向一般的转变，学生的视线和思维随着点P在垂直平分线上的移动变化而变化着，通过作图、度量，他们依然会发现特殊位置上的结论一般化后依然成立.基于这样的获得，教师立即引导学生进行了“理论”上的“证明”，让他们用“最近学过的知识来说明”这个结论.由于有了“全等三角形”的基础铺垫，有了轴对称的性质认知，让学生给出严格论证的方法还是较为容易的.所以教学过程中，教师的步步追问，让已有知识不断被唤醒，学生在提取和应用中顺利地得出了证明的方法，为最终结论的归纳扫清了障碍.教师从“特殊”出发，引导学生归纳的“一般”规律，让学生从熟悉的图形中抽取出新的、符合学生认知规律的结论，并进行了规范化验证，整个教学严谨、规范，具有很强的新意.

二、教学感悟

1.关注新旧衔接，建构新知教学起点

数学新知的学习离不开旧知的支撑，我们在教学设计时只有关注了新旧知识之间的衔接，才能建构出有效的教学起点，才能形成有利于学生获得数学知识的“源”.以“线段的垂直平分线的性质”为例，支撑这一新知学习的旧知有“全等三角形的性质和判定”“垂直平分线的概念”“轴对称的性质”等，在本文所述案例中，教者正是从这些旧知中进行了深度挖掘，将教学的起点定格在“中点”，也就是“垂直平分线的概念”之上，让学生的新知探究从这个点上展开，教者通过对点P的位置的变换，让新知由“特殊”逐步走向“一般”.最终，通过各种旧知的不断叠加，新知不再停留在“猜想”之上，各种不同方法的证明给出了“新知是正确的”的充分依据，这也保证了学生在接下来的应用中“底气十足”.从案例中的教学设计看，教师从学生旧的知识网络中，不仅找出了新知的生成基础，还设计出了“线段的垂直平分线的性质”教学“生长点”，这样的分析与设计紧贴学情，符合学生的认知规律，能取得较好的教学成效也就在情理之中了！

2.找寻新知“特性”，强化数学思想渗透

数学思想是学生解决数学问题的重要工具，在学生的数学学习和应用中有着非常大的作用.因此，在初中数学教学中，我们应高度重视数学思想的教学，要注意用好教学内容中的“思想素材”，及时将数学思想渗透到教学进程之中，以便学生及时感悟与积累.这种基于教学内容的渗透，应建立在教师对教学新知“特性”的充分剖析之上，是对新知“特性”充分把握下的自然“镶嵌”.显然，为数学思想找寻教学载体自然而然地成为了教师的“必修功课”.数学新知一般都有着自己独特的“个性”，这些“个性”将是我们加载数学思想最重要的渠道.举两个例子，在教学“数轴”时，数轴是学生在初中阶段首次数形结合形成的工具，抓住数轴的这一“个性”，教师就可以在教学中顺利加载数形结合思想，让学生在获得“数轴”的概念及作法的同时，也能对这一初中阶段的核心数学思想有所感悟；在教学“圆周角定理”时，教材安排了三种不同图形下的定理推导，教师就应根据教材的设计，在帮助学生获得定理的同时，将分类讨论思想渗透进去……再说说本文中的这则案例，教师也是抓住了“中点”和“垂直平分线”之间的关系，从“特殊”入手，通过多次同一结论的陈述铺垫，最终归纳出“一般”规律.在这一过程中，学生对“特殊与一般”思想的感悟还是较为深刻的.

3.重视“过程”教学，形成活动经验积淀

在学生获得数学知识的进程中，参与思维过程的不只是已有的数学知识与技能，还有一些“默会知识”，比如数学活动经验的参与.由此可见，知识获得的过程，实际上也是学生基本活动经验的提取与应用的过程.毋庸置疑，知识的获得过程同样是学生积累新的数学活动经验的过程.因此，我们应重视新知获得过程的教学，要让学生实实在在地经历知识的完整生成过程，要让他们清晰感知到在不同的教学时点上，基础知识、基本技能、基本思想和基本活动经验各起到了什么作用，有哪些知识与经验是可以继续延续应用的，又有哪些新的知识与经验自然生成了，可以在后面的学习中发挥作用.这些源自教学过程的切身感悟，应是教师和学生互动交流的结果，我们应鼓励并帮助学生“明明白白”地获得数学知识.案例中，为了帮助学生“明明白白”获得“线段的垂直平分线的性质”，学生从线段的中点出发开始初步感知，随着教师呈现出的点P的变化，学生的思维一路跟来，“线段垂直平分线上的点到两个端点的距离相等”成为了共性的规律.为了让这一结论得到所有学生认可，在教师的引导下，学生分别应用所学过的知识进行了必要的论证.这样的过程经历，保证了知识的获得具有个性特征，是一种基于个体认同的共性归纳，无论是探究的终极知识，还是隐藏于探究交流中的活动经验，都是顺其自然下的生成，合理、扎实、有效.

三、写在最后

数学基本思想是数学“四基”之一，是与学生数学学习与数学应用密切相关的“默会知识”，在学生的学习与生活中作用明显.所以数学教学应重视数学思想的教学.在几何教学中，“特殊与一般”是学生获取数学结论最常用的数学思想，几乎贯穿于初中整个学段的几何教学.在几何教学中，我们常会引导学生从特殊位置出发，去探究其中可能存在的特殊的数量关系或位置关系，在学生获得特殊状态下的“猜想”后，再围绕可能成为的一般结论进行必要的证明.不难看出，在形成猜想、获得结论、验证结论的过程中，学生的思维随着探究的不断深入被迅速拓宽.附着于一般性结论之上的其他“三基”（基本技能、基本思想和基本活动经验）都将会随之“固化”，成为学生“学习成果”的一部分.接下来的应用，将会是这些一般结论的特殊化，无论是基础知识、基本技能这些显性知识，还是数学思想、数学活动经验这些隐性知识，都会得到进一步的强化，于是乎，学生个体的数学素养随之提升！

以上，仅是笔者一家之言，不足之处，敬请各位同行专家批评指正！

参考文献：

1.朱正南.生成在意料之外处置于情理之中——以“三角形全等的判定（AAS）”为例［J］.中学数学（下），2013（5）.

2.王冰.重视过程教学发展思维能力——“12.1轴对称（第2课时）”的教学设计及其特点［J］.中国数学教育（初中版），2013（6）.

3.中华人民共和国教育部制定.义务教育数学课程标准（2011版）［M］.北京：北京师范大学出版社，2012.

4.陈先荣.把“软任务”提升为“硬指标”——对课程目标从“双基”发展到“四基”的认识［J］.中学数学杂志（初中版），2012（3）.

5.宋庆莉.数学教学应从学生的“基本活动经验”抓起［J］.教学与管理（中学版），2014（6）.

6.张春莉.课例：16.2线段的垂直平分线（第一课时）［J］.中学数学教学，2012（3）.