作图教学:述理与述法并重——以“过直线外一点作已知直线的垂线”为例
2016-05-03江苏省如皋市东陈初中杭石琴
☉江苏省如皋市东陈初中 杭石琴
作图教学:述理与述法并重——以“过直线外一点作已知直线的垂线”为例
☉江苏省如皋市东陈初中杭石琴
尺规作图是学生的基本数学技能之一.对于尺规作图,我们不仅要让学生知道作图的基本步骤,还要让他们知晓实施这些步骤的理由.显然,尺规作图教学,我们不仅要让学生“知其然,还要知其所以然”.也就是说,我们应同时将作图的理由和作图的方法在尺规作图教学中加以明晰,让学生清楚尺规作图的知识基础、技能基础和思想方法基础,使今后的尺规作图能够明明白白、清清楚楚.笔者近期在执教“过直线外一点作已知直线的垂线”时,借助学生已有知识先明晰了作图的理由,再让学生结合具体情境探究作图的方法,取得了不错的成效.现将这次教学的历程与各位做个分享,希望能给您带来启示.
一、教学片断及分析
1.知识应用,提前述理
通过探索,学生刚刚获得了“与一条线段两个端点距离相等的点,在这条线段的垂直平分线上”.
师:如图1,如果PA=PB,那么点P在AB的垂直平分线上吗?
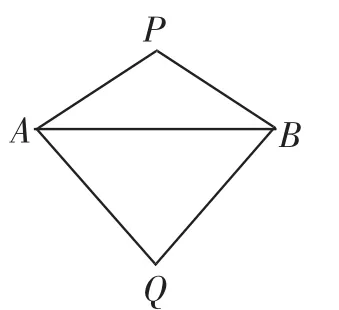
图1
生(齐):在!
(教师在图1中补作点Q)
师:如果QA=QB.请问,点Q也在AB的垂直平分线上吗?
生(齐):在!
师:PQ与AB有怎样的关系呢?
生1:PQ垂直平分AB.
师:为什么?
生2:根据刚刚得到的结论,点P在AB的垂直平分线上,Q也在AB的垂直平分线上,所以PQ垂直平分AB.
师:为什么?
生3:两点确定一条直线呀!
师:非常好!看来,只要能找到“到线段两个端点距离相等”的两个点,就可以作出这条线段的垂线了!
2.自主探索,述法究理
师:接下来将利用刚刚所获得的知识与经验,来探索一个新的基本尺规作图:过直线外一点作出已知直线的垂线.(教师板书)
投影:
已知:直线MN和MN外一点P(如图2).
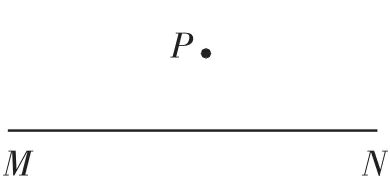
图2
求作:MN的垂线,使它经过点P.
学生活动:探究作图方法,并在小组内交流.
10分钟后小组交流结束,教师请一名学生展示作图过程,如图3.
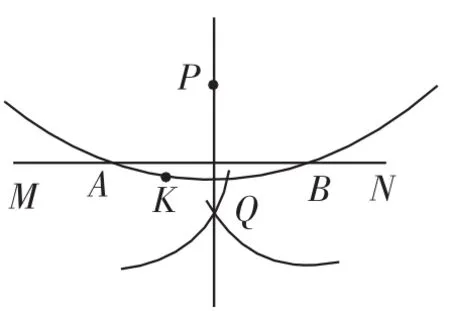
图3
生4:我先以P为圆心、任意长为半径作圆,与MN交于两点A、B.再分别以A、B为圆心,任意长为半径画弧交于点Q.作直线PQ,PQ就是MN的垂线.
师:你能说说这么作图的理由吗?
生4:作第一条弧,是为了找到图3中的点A和点B,使得PA=PB.
师:那么,作第二、三两条弧呢?
生4:得出点Q,使得QA=QB.
师:得出的直线PQ是MN的垂线吗?
生5:是的!
师:为什么?
生5:根据刚才的探究,PA=PB,QA=QB,点P、Q都在AB的垂直平分线上,所以PQ⊥AB.
师:太棒了!看来你不仅知道怎么去作,还知道了为什么可以这么做!
3.步骤微调,完善作法
师:在你们的作图过程中,三个关键点A、B和Q都出现了吗?
(有学生在摇头,示意并没有全部出现)
师:怎么会没出现呢?
生6:作第一条弧时,半径必须比较长,太短了与直线MN就没有交点.
师:哦!原来是这样啊!有没有什么方法能保证半径的长度适宜呢?
生7:我们可以先在MN的下方取一点K,(快步走到黑板前,添上点K,如图3)以P为圆心、PK为半径作圆.
师:这是个不错的主意!还有什么值得注意的地方吗?
生8:以A、B为圆心作弧时,半径要比AB的一半长,否则也会没有交点.
师:是的!看来今天的作图还有很多地方是要注意的,大家一定要小心哦!(教师投影完整的作图步骤,并进行了示范作图)
师:通过刚刚的探索,我们不仅探究得出了“过直线外一点作已知直线的垂线”这一基本作图的作法,并且知道了这一作法的数学道理.今后的尺规作图学习,我们也将从方法和理由这两个角度展开学习,希望今天的学习能给后面的学习提供帮助.
二、片断分析
这是从学生刚刚获得的几何知识入手,将由定理生成的基本图形进行复合,形成图1,对图1展开深度探究,通过层层追问,使学生知道了点P和点Q都在直线MN的垂直平分线上,进而抽象出“只要能找到‘到线段两个端点距离相等’的两个点,就可以作出这条线段的垂线了”这一作垂线的方法,这实际上也是“过直线外一点作已知直线的垂线”的方法.至此,本节课要探究的尺规作图的基本理由已经陈述完毕.接下来,教师直接抛出了本节课探究的话题,让学生利用刚刚获得的知识自主探究,并将探究的结果在小组中进行交流.有了前面知识和经验的铺垫,学生不负众望,顺利给出了作图的方法.在接下来的全班交流中,就是紧扣学生给出的方法,通过反复提问,将作图的每一个步骤都与数学知识紧密关联在一起,让述法与述理同步进行,作图不再是“孤单”的程序化的步骤,而是与数学基础知识、基本活动经验紧密联系在一起的数学基本技能,理论与实践紧密地结合在了一起.针对学生探索中出现的一些问题,教师展开进一步矫正,给出了完整的作法,并通过投影和自身的演示将作图步骤和作图过程进行了“定格”,让每一位学生“知其然,且知其所以然”,实现了数学教学由知识向方法的完美过渡.
三、几点感悟
1.理法同行,谁都不是“教学鸡肋”
尺规作图是初中数学教学的主要内容.传统教学,对作法教学非常重视.至于作图的理由,教师在教学中一般都一带而过,不作为教学的重点呈现,使得作图述理沦为“教学鸡肋”.《义务教育数学课程标准(2011版)》(下称“课标(2011版)”)对尺规作图提出了明确要求,要求我们不仅要重视作法教学,还要重视作图理由的教学.“理法同行”是当下初中数学课堂尺规作图教学的基本要求,一线数学教师应努力落实.本文案例中,教师将这一理念很好地落实到了教学实践中.在作图方法探究之前,教师就已经提前将作图的理由进行了“预埋”,借助本节课获得知识的应用,将尺规作图成果中的基本作图(图1)展示在学生面前.接下来的探究是对知识应用的再度顺应,有了图1的铺垫,作图方法探究就变得非常顺利了.然而当学生给出作法后,教师并没有就此停住,而是将作图理由进一步明晰.应该说,整个教学过程中,理与法同行,谁都不是“教学鸡肋”,它们都是教学的主要内容,是师生交流互动探究的核心话题.
2.理法并述,强化数学“四基”教学
尺规作图,是初中数学最重要的基本技能之一,是学生获取数学结论、探究解题思路与验证数学猜想的重要工具.就问题解决而言,复杂的数学问题的化解,需要借助尺规作图来呈现所有的“可能”,这些“可能”与数学的基础知识、基本技能、基本思想和基本活动经验紧密联系在一起.因此,想要学生作出符合要求的图形,就必须充分调动已经获得的“四基”.所以在尺规作图教学中,我们就不能只强调作图的方法,而应将作图步骤与数学“四基”关联在一起,使学生形成知识提取应用的有效网络.以本文中的案例为例,“过直线外一点作已知直线的垂线”这一尺规作图只用了“垂直”,但我们从这个作图教学的前奏和后延看,垂直平分线的性质与判定是绕不开的一个“坎”.在教学中,我们就应从垂直平分线入手,当他们获得这一基础知识后,给予适当练习,一方面巩固旧知,另一方面让学生的认知又向前迈出一步,逼近所要获得的作图方法.当学生获得作图方法后,教师还应将作法与已经获得的基础知识关联起来,让学生的技能形成与知识获得同步.
3.理法并重,相互促进共“谋”发展
过去的尺规作图教学沿袭了数学教学“重实践”的特点,重视作法教学,这是非常可贵的.在“课标(2011版)”颁布后,对尺规作图教学提出了“要重视作图理由”的要求.一线教师对此高度赞同,并努力将课标理念落在了实处,他们将述理与述法放在作图教学的同一个高度上,使两者成为作图教学的“左膀”与“右臂”.随着作图教学的不断深入,我们发现“理法并重,能有效推动学生的数学认知不断走高”.当学生的知识到达较高的位置后,便会从道理上给予作法更准确的支持,使学生能够更加清晰地掌握尺规作图的基本步骤;当尺规作图的技能渐趋熟练时,高位的技能展示将会给学生数学问题的深度探究注入不竭动力,随之而来的便是基于作图之上的新的知识生成、思想感悟和经验积淀.这样的相互依存,共同促进,让知识与技能混合在一起,组合出现,很好地服务于学生数学知识的获得和数学问题的解决.我们有理由相信,随着学生数学知识的不断积聚,有着理论支撑的作图技能将会嵌入到学生的知识网络之中,成为个人素养的重要组成部分.
参考文献:
1.王冰.重视过程教学发展思维能力——“12.1轴对称(第2课时)”的教学设计及其特点[J].中国数学教育(初中版),2013(6).
2.印冬建.明理:尺规作图教学的新要求——以“作一个角的平分线”为例[J].教育研究与评论(中学教育教学),2012(12).
3.中华人民共和国教育部制定.义务教育数学课程标准(2011版)[M].北京:北京师范大学出版社,2012.
*本文系江苏省教学科学“十二五”规划课题《初中数学“微话题探讨式学习”教学策略研究》(编号:E-c/2013/8)的研究成果.
