初探折纸中的数学

折纸，是日常生活中学生喜闻乐见的一种游戏，也是贴近生活的一种数学素材，“折纸型”问题广泛出现于中考试题、学生综合实践之中。折纸能锻炼学生的动手操作能力、空间想象能力和数学建模能力，其中蕴含着较为丰富的数学思想，在当前课程改革中日益凸显其重要性。在初二教学中，就有这样一个折纸问题。

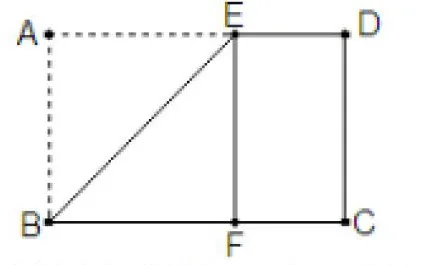
【课本原题】把一张矩形纸ABCD折叠后，沿EF裁下，可以得到一个正方形纸片，为什么？

说明：此题的证明方法很多，可以通过证明“4边相等+一个直角 正方形”；也可以通过证明“3个直角+一组邻边相等 正方形”。利用的是折叠时重合的线段和角产生的相等关系。

为了让学生理解并熟练运用相关的相等关系，针对折叠时产生的“相等的角和相等的边”两个重要结论进行了系列探究。

一、折叠产生相等的角

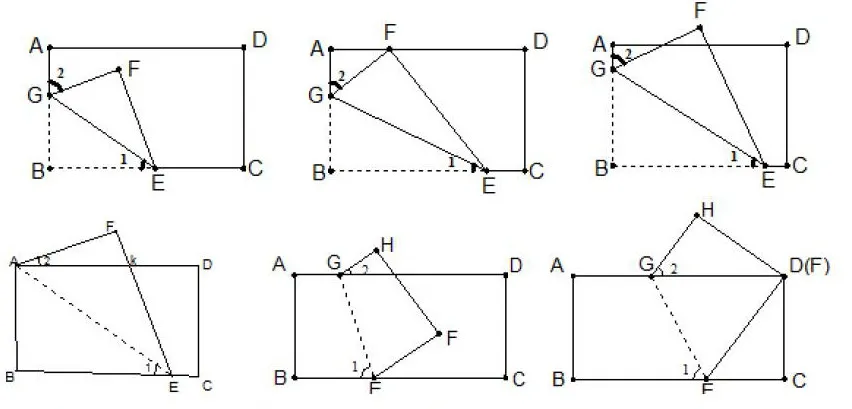
变形1：把一张矩形纸ABCD随意折起一个角或一边，若已知∠1的大小，能求出图中∠2的大小吗？学生折出各种图形，整理后有如下：

分析：易证明∠BEG=∠GEF，上面三个图形中利用Rt⊿BEG可得∠BGE的度数，从而知∠FGB的度数，通过互补关系得∠2的度数；下左图中通过AD∥BC可得∠AKF的度数，再通过Rt⊿AKF的两锐角互余得∠2的度数；最后两个图形通过GH∥EF，得∠EGH，通过AD∥BC得∠EGD的度数，两者相减，即得∠2的度数。

二、折叠产生相等的边

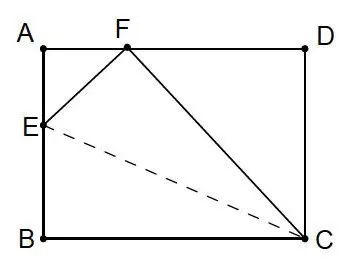
变形2：把一张矩形纸ABCD沿着CE折叠，如图使B点落在F处。已知：AB=8cm，BC=10cm，求AE的长。

分析：由于翻折，易得CF=BC=10cm.同时产生2个直角三角形：Rt⊿AEF、Rt⊿CDF，在Rt⊿CDF中，易得DF=6 cm，AF=4 cm，再转入Rt⊿AEF中设AE=x，列出方程42=x2+（8-x）2，求得AE=3cm.

根据勾股定理列出方程作为解决问题的途径.而选用勾股定理所在的直角三角形，我们也注意到一般是折叠后形成的新直角三角形。

三、综合运用相等的边和角

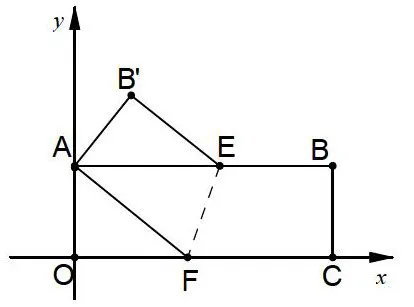
变形3：矩形ABCD，B（9，3），沿EF折叠，使C落在A处，B落在B’处，求（1）折痕EF的长；（2）EF所在直线的解析式。

分析：在Rt⊿AOF中利用勾股定理可求出AF=5，由等腰三角形⊿AEF 可知AE = AF =5，因此作EG⊥OG交OG于点G，可得E（5，3），FG=1.在Rt⊿EFG中求得EF= ；同时可知F（4，0），从而可以求出EF的解析式.

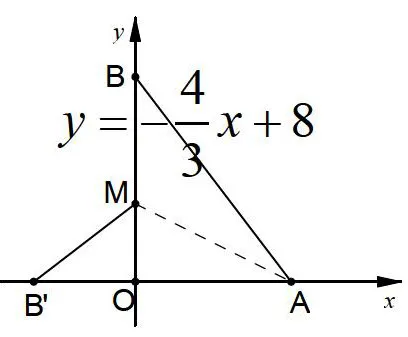
变形4：将⊿ABM沿AM折叠，使B落在B’处，直线AB的解析式为 ，求AM所在直线的解析式.

分析：由AB的解析式可知：OA=6，0B=8，从而得AB=AB’=10。要求AM解析式，就是求M点坐标，即OM的长度。所以在Rt⊿OB’M中利用勾股定理可求得OM=3，即M（0，3）。AM所在直线解析式为：

通过折纸，让学生感受到在生活中处处都有数学，课后，教师可以引导学生对折纸题目及时进行总结，也许会发现蕴藏在“折纸”中的更多奥妙。当然，折纸本身并不能完全取代对数学活动的分析，通过积极开展对数学中游戏娱乐的探索，将会对培养学生的“自动力”，培养学生敢于创新的“自动”精神极为重要。

（作者单位：苏州工业园区星湾学校）