创设问题导引激活课堂思维———以三角恒等变换教学为例



创设问题导引激活课堂思维
———以三角恒等变换教学为例

◇内蒙古吴贵铎

三角函数是高中数学主干内容之一,涉及公式、定理较多,部分教师在讲解此知识模块时,只是强调学生机械地记忆,没有将知识的前后关联及定理的内涵讲清、讲透,致使学生思维出现断层,只是机械地应用,不能形成系统．以下是笔者在教学中几个片段,与同行分享．

1知识回顾

问题1求函数y=Asin(ωx+φ)相关性质．

师:前面我们已经学习了y=Asin(ωx+φ)相关性质处理,请同学们来回忆一下．

生1:将ωx+φ看作整体,结合函数y=sinx的性质,即可得出了y=Asin(ωx+φ)相关性质……

师:请同学们具体来说一下y=2sin(2x+π/6)的相关性质．

生2:……(过程略)

问题2和差倍角公式.

师:sin(α±β)=?

生3:sin(α±β)=sinαcosβ±cosαsinβ．

师:cos(α±β)=?

生4:cos(α±β)=cosαcosβ∓sinαsinβ．

师:sin 2α=?cos 2α=?

生5:sin 2α=2sinαcosα

cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α.

师:公式的应用包括“正用”“逆用”“变形用”,如何逆用?

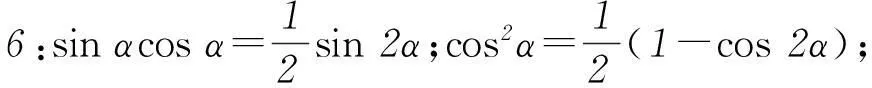
2问题探究

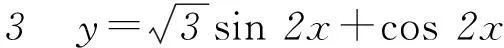
生众:沉默…

师: (并未直接讲解,而是提了新问题) 将y=2sin(2x+π/6)展开.

生7:利用两角和的正弦公式

y=2sin(2x+π/6)=2(sin 2xcos(π/6)+

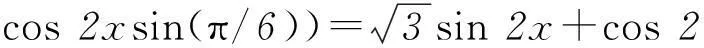
生众: (豁然开朗)这就是上面所求的问题呀!只要把展开式逆推回去就可以了．

师:好办法.如何逆推?

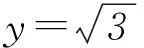
师:精彩!利用已有知识,成功地解决了新的问题.

练习:(1)y=sin 2x+cos 2x．

师:根据上面的分析,如果对于一个一般的函数y=asinx+bcosx,如何转化,求相关性质?

生9:按转化的方式分析,asinx+bcosx中的a为某一角度的余弦值,b为同角的正弦值．

生10:不对,a和b有可能大于1.

师:说得好!如果a和b均大于1,该如何处理?

生10:a与某一角度的余弦值有关,b与同角的正弦值有关,但b与a的比值,即该角的正切值,就不受a与b是否大于1的影响了,故可用正切来表示．

师:太精彩了!继续……

生10:如果设该角为φ,即tanφ=b/a.则

3问题拓展

问题4求y=2sinxcosx+cos2x的相关性质．

师:我们可以将问题变得再复杂一点,如何求函数y=2sinxcosx+cos2x的相关性质?

生11:可以将函数y=2sinxcosx+cos2x化为y=asin 2x+bcos 2x形式．

师:非常好!如何化?继续……

生11:可逆用我们前面推导过的二倍角公式,得

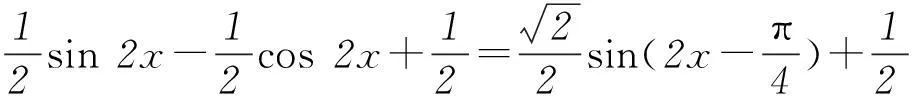
进而化为我们熟悉的类型y=Asin(ωx+φ),利用上述办法求解．

4高考题演练

问题5已知函数

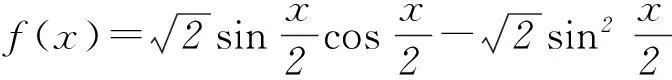
求： (1)f(x)的最小正周期;

(2)f(x)在区间[-π, 0]上的最小值.

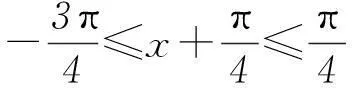
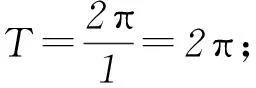
在知识讲解的整个过程中,教师一直处于引导地位.通过问题导引,引导学生一步步得出结论,使学生一直处于问题的探究之中,规律的发现及结论的得到都是通过学生的观察、分析得来的.整个教学过程中学生积极参与其中,由被动接受者转变为主动探究者,在探究的过程使学生认识到了所学知识之间的关联,弄清了公式的来龙去脉,不仅将所学知识形成系统,而且将其内化为解题能力,落实了新课改的理念．

(作者单位：内蒙古正镶白旗察汗淖中学)