一个绝对值不等式恒成立问题的错解辨析



一个绝对值不等式恒成立问题的错解辨析

◇甘肃马生兰

绝对值不等式恒成立问题是高考的一个热点,也是一个难点,这类题目要求考生有较强的逻辑推理的能力和对分类讨论数学思想的正确认识和把握.近期一位学生递交了一个绝对值不等式恒成立问题的解法,他的答案与原答案不一致,但是他认为解题过程是正确的,想请老师帮他确认一下.在看了他的解题过程之后,和他进行了一番辨析,最终帮他找到了错解的原因.今天将这道题的错解辨析呈现出来,以期对读者有些启发,避免在该问题上重蹈覆辙.

错解原不等式恒成立等价于

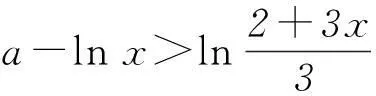
①

②

对于任意的x∈[1/6,1/3]恒成立.

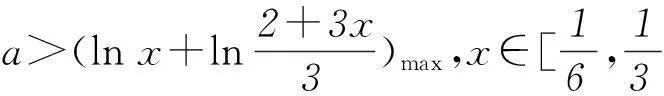
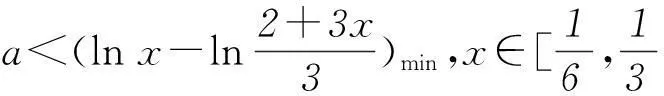
解题理论依据:当D为某区间时,|f(x)-a|>g(x)对任意x∈D恒成立等价于不等式f(x)-a>g(x)或f(x)-a<-g(x)对任意x∈D恒成立.

剖析原理:该理论依据是错误的,错在二者不是等价关系,原不等式恒成立的等价条件是“不等式f(x)-a>g(x),对任意x∈E恒成立或f(x)-a<-g(x),对任意x∈F恒成立(其中E∪F=D)”.

下面正确解答原命题.

分析1对不等式右边的代数式的正、负讨论,达到去绝对值的目的.

所以a∈{a|a∈R,a≠ln(1/3)}.

分析2将原不等式恒成立转化为2个非负代数式的和为正数,原不等式恒成立,必须满足2个代数式均不为0.

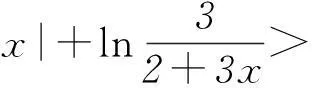
|a-lnx|≥0,ln[3/(2+3x)]≥0,

分析3利用“正难则反”的解题原则,先求原命题的否定命题的a的取值范围,再利用补集的思想,求出原命题恒成立时实数a的取值范围

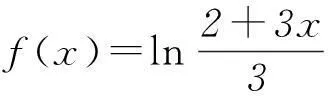
以上对绝对值不等式|f(x)-a|>g(x)恒成立的错解辨析,可以得出错解的原因是:将该绝对值不等式恒成立的等价条件误认为与绝对值不等式解集的等价条件一致，即“不等式|f(x)|>g(x)的解集”的等价条件是“不等式f(x)>g(x)的解集,或f(x)<-g(x)的解集”.所以解决绝对值不等式恒成立的问题的关键在于命题的等价转化,或者利用分类讨论,或者利用“正难则反”的原则,可以顺利地解决问题,甚至找到解决问题的最简捷的途径.

(作者单位：甘肃省积石山县积石中学)