浅谈三角函数变换技巧
2016-04-28赵飞
浅谈三角函数变换技巧
◇辽宁赵飞
一般来说,三角函数的转换具有不定性、多向性,这就使得在解题的过程中出现了多种多样的方法.但无论怎么进行变换,解题的基本规律和基本思想是不会改变的.
1常见三角函数变换类型
1.1变换函数名称
函数名称变换是三角函数变换中比较常见的类型,其中的切、割化弦又是最为常见的函数名称变换.此变换主要考虑化形式和化函数2个方面,正弦和余弦在三角函数中应用最广,并且是6个三角函数的基础,正切和余切次之.常见的函数名称转化方式有2种:弦化切,切割化弦.
1.2变换三角函数的“角”
三角函数中的“角”主要指的是补角、余角、半角、差角,三角变换的表现形式之一就是对这些“角”实施变换.当这些三角函数的“角”在变化的时候,运算过程中的一些相应的函数名称和符号等都会随之而变化.利用三角之间的半、差、和、余、补等关系,将未知角用已知角表示出来,再利用相关的关系进行运算,这样三角函数问题就顺利地解决了.


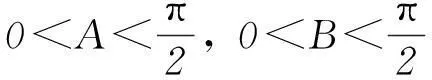

因为cos(2A+B)=3/5>0, 0<2A+B<3π/2.所以0<2A+B<π/2,sin(2A+B)=4/5,所以
cosB=cos [2(A+B)-(2A+B)]=cos(2A+2B)·
cos(2A+B)+sin(2A+2B)·sin(2A+B)=

1.3变换三角函数的“形”


2常见三角函数变换解题技巧
2.1弦、切互化
弦、切互化是在三角函数题目解答中比较常用的基础方法.利用弦化切的方法将三角函数中存在的正切函数进行化弦后,再进行问题的证明和解答.
2.2等量代换角
在解题的过程中,首先判断已知角和未知角之间是否存在着某种关系.若存在确定的关系,可以利用角的等量代换进行转化.如θ=(θ+φ)-φ=φ-(φ-θ)=(θ+φ)/2+(φ-θ)/2.这样通过角之间简单的转换,将比较复杂的问题变成平时经常解决的问题,进而简单求解.
2.3逆用公式或变用公式
在解题的过程中,可以采用逆推的方法进行解答,就是从结论开始逆向探究条件.公式也可以经过变换后再使用,这样的解题方法有时能起到很好的效果.但在使用的过程中,必须对公式及其证明很熟悉.例如2sin2x=1-cos 2x,2cos2x=1+cos 2x等.让学生对公式的证明以及由公式推导出来的相关结论熟练掌握,如此才能做到熟能生巧.
综上,三角函数的转换思想,是找出差异、建立联系、选对公式、促进转化.本着这个基本思想来解题,即可顺利找到解题的方向,化未知为已知.选择正确的定理和公式,找出角或者是函数名称间的差异,无论题目怎么变换,都可以做到化繁为简、轻松解答.
(作者单位:辽宁省建平县实验中学)
