化归转化思想在高中函数教学中的运用



化归转化思想在高中函数教学中的运用

◇广东郭易萍

在高中数学教学过程中,往往会遇到一些较为复杂的问题,直接求解较为困难．若对这些问题进行转化和归类,则可使问题变得简单易解．这种解决数学问题的思路和方式,就是化归转化思想,它是高中数学中十分重要的思想之一．在高中数学教学中,函数是重点和难点,贯穿整个高中数学教学过程的始终．由于函数的抽象性,给教学活动带来了一定的困难．因此,如何在函数教学中恰当运用化归转化思想,具有十分重要的意义．

1化归转化思想的内涵

化归转化思想的运用具有很大的复杂性和多向性,解决问题的关键在于条件转化的合理性．在条件转化的过程中,不但可以转化问题的条件,同时也能够转化问题的结论．也就是说,无论是对于问题的外部形式还是内部结构,都能够进行转化,由此体现出了化归转化思想的多向性特征．从宏观的角度上来看,将化归转化思想运用在高中数学教学中,能够充分地对各种解题技巧和数学方法进行合理的利用,从而在高中函数教学中,提供更多的解题方法和思路．

利用化归转化思想解决高中函数问题时,可以将需要解决的问题转化为新的问题．由于新问题是已经学过和了解的内容,同时解题方法也十分熟悉,因此能够轻易得到新问题的答案．然后利用新问题的答案,对原始的问题进行还原,从而得出原始问题的答案．在这一过程中,虽然解决问题的程序看起来较为复杂,但解题过程中的每一个环节和步骤都是在自己的知识范围之内,能够进行较为理想的掌控．因此,运用化归转化思想对高中函数问题进行求解,能够有效地提高解题效率和准确率．

2高中函数教学中化归转化思想的实际运用

2.1化未知为已知

化归转化思想的运用,能够有效地提高函数的解题效率．例如,在三角函数求最值问题中,化归转化思想就是最常运用的解题思路,将未知的三角函数转化为已知的二次函数后再求解．

y=(m2-1)/2+m=(m+1)2/2-1．

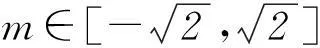
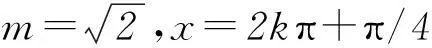
当m=-1,x=2kπ+π或x=2kπ+3π/2,且k为整数时,ymin=-1．

通过上述的解题方法对学生进行教学,能够让学生在面对未知问题的时候,对问题迅速做出适当的转换,从而求得最终结果．

2.2化正面到反面

在高中函数教学中,在很多问题的解答中,如果从正面入手,难度将会很大．对此,可以利用问题中给出的条件,从反面入手进行化归转化．这种解题思路也是高中函数教学中常用的方法之一．

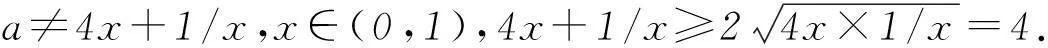
2.3化数为形

通过数形之间的化归转化,能够增强函数的直观性,从而快速、准确地解题．在教学中,运用化归转化思想能够提高教学效率,使学生更好的理解解题方法和思路．

2.4化一般为特殊

抽象函数因没有具体的解析式,因此成为学生解题的难点．解题中若能充分挖掘题目条件,联想特殊的函数模型,常可化抽象为具体,进而简洁解题．

通过构造“具体函数”来描述抽象函数,用特殊来代替一般,使问题得以简洁求解．

除了上述几种化归方法外,在当前的高中数学函数教学中,还有对不等与相等之间的化归、变量与常量之间的化归等多种化归方式．在当前高中函数教学过程中,数学思想发挥着决定性作用．学生在完成一定的数学理论知识学习后,应当学会如何在解实际问题中加以运用．在遇到新题型的时候,能够熟练地运用化归思想,将未知的题型化归为已知的知识,从而解决实际问题．这样不但能够提高教学效率,取得更为理想的教学效果,还能够培养学生思考和解决问题的能力,对学生综合能力的提高具有很大的帮助．

在高中函数教学中,除了进行理论知识教学之外,还应当注重对学生数学思想与解题思路的培养．否则,学生虽然在课堂中能够听懂,但是课后却难以解决实际的函数问题．对此,教师应在教学中充分运用化归转化思想,引导学生对问题进行适当的化归,从而更加快速、准确地解决函数问题．

(作者单位：广东佛山市南海区西樵高级中学)