例谈“函数”观点在解题中的活用



例谈“函数”观点在解题中的活用

◇江苏桂燕

函数是高考的重点和热点,其考查形式既可以作为考点，也可以作为方法.本文以归类举例的形式具体说明灵活运用“函数”观点巧解有关非函数类试题.

1巧解数列问题

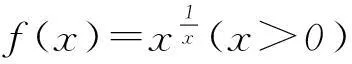
2巧解平面向量问题

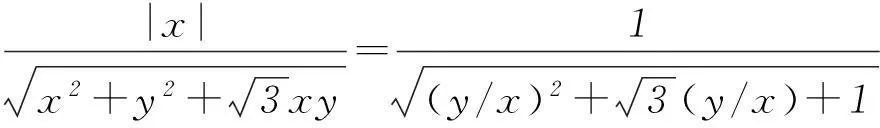
①

设t=y/x,则

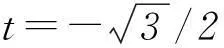
3巧解不等式问题

令函数h(x)=f(x)-x=x3-12x,则h(x)在(2m,m+1)上单调递减.由h′(x)=3x2-12=3(x+2)(x-2)知函数h(x)的单调递减区间为(-2,2).

4巧解二项式问题

-2 015(1-x)2 014=a1+2a2(x-3)+

3a3(x-3)2+…+2 015a2 015(x-3)2 014.

取x=2得

a1-2a2+3a3-4a4+…-2 014a2 014+

2 015a2 015=-2 015(1-2)2 014=-2 015.

故所求值为-2 015.

5巧解三角最值问题

A最大值为1,最小值为2/5;

B最大值为5/2,最小值为1;

C最大值为1,最小值为3/5;

D最大值为5/2,最小值为3/5

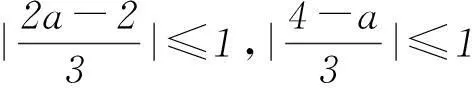
6巧解方程问题

2t+3t+t+1/6=0,

这是一个超越方程,所以不能用常规方法求解．可构造函数

f(t)=2t+3t+t,

那么f(t)=-1/6,所以f(t)=f(-1),又因为f(t)是一个递增函数,所以t=-1,即x2-2x=-1,所以可得出这个方程的解就是x=1．

总之，灵活运用“函数”观点,往往有助于我们巧妙分析、解决问题,从而不断积累解题经验,逐步提升解题技能

(作者单位：江苏省扬州市广陵区红桥高级中学)