从一道填空压轴题谈数学直觉思维的培养



从一道填空压轴题谈数学直觉思维的培养

◇江苏顾雪1吴建明2

在传统的授课方式中,教师只强调思维的逻辑性、解题的严谨性，而忽视学生的数学直接思维的培养，久而久之就会导致学生对枯燥乏味的推理失去兴趣和信心,在遇到较难解决的数学问题时会缺乏研究探索的意志．但是如果教师在上课时鼓励学生去猜想,让学生畅所欲言,并加以引导，那么,学生的数学直觉思维能力就会在不知不觉中得以培养，提高解决难题与陌生题的信心,增强数学问题自主探索能力．

下面是高三数学模拟考试的一道填空压轴题,教学中笔者让学生去自主发现解决问题的方法,哪怕是不完整的解答．

具体教学活动如下:

拿出题目后为了防止对学生的直觉思维产生干扰,笔者没有加以分析,让学生思考大概1 min就叫了一位学生回答．

生1：(胆怯)不会．

教师：(鼓励)那你说说此题可能会涉及到函数的什么性质？

生1：我猜是函数的单调性,只是不知道如何利用函数的单调性来求解．

生2：是不是要用到导数研究函数的单调性？

教师:如果函数是增函数,你们能解决吗?

学生不语,因为发现即使知道单调递增,也无法利用“f[u(x)]>f[v(x)]”的形式来求解．

学生并未给出解答过程,只是一个思维片段．其实这一步在解题过程中是非常关键的,而它的发现只是学生觉得“对称”．随着思维的打开,又有学生对题设作出了大胆猜想.

生4:老师,你说的“函数是增函数”是不是因为f(x)+xf′(x)>0,我发现了f(x)+xf′(x)是xf(x)求导的结果,可以把xf(x)看成一个整体,使

转化为2个函数值的大小了．

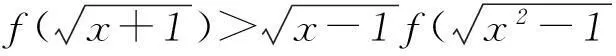
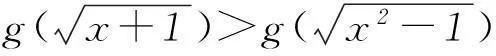
直觉思维与逻辑思维既对立又统一．法国数学家彭家勒(H.Poincaré)说:“逻辑用于证明,直觉用于发明．”这恰好说明了数学问题的发现往往是源于“不合规矩”的直觉思维,发现后的论证则要经过严格的逻辑推理证明．直觉思维可以帮助学生理解教学的内容,拓展学生解决问题的思路．一些学生找到解决问题思路的依据是数学灵感,他们打破了数学逻辑思维的束缚,直接发现了数学问题的内在关系,从而发现了解决问题的方法．这里所提到的数学灵感就是直觉思维．数学的直觉思维能够对具有相似结构的数学问题产生顿悟,能够短时间内寻求到解题途径．

数学直觉思维能力是可以通过训练提高的．首先,直觉思维虽具有偶然性,但并不是“碰巧”,平时教师要加强对基础知识的巩固和训练．只有扎实的基础知识才能激发学生的灵感．其次,平时在教学过程中,教师要注重学生直觉思维能力的培养,引导学生举一反三,建立合理的知识体系,尽量帮助学生构建数学知识网络来进行数学学习．再次,教学活动中巧妙设置情景,鼓励学生大胆猜想,锻炼学生数学直觉思维能力,提高思维的灵敏性．最后,不必担心学生思考过程中犯错误,要让学生在思考过程中适当的走一些“歪路”,找到解决问题的合理方式．在这个过程中,教师可以及时地观察学生的思维动态,针对不同的思维特点进行有效的教学,同时也培养学生的探索精神,发展学生的数学直觉思维能力．