中立型时变时滞BAM神经网络状态估计器的设计

刘　佳，张运喜

（天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津300222）



中立型时变时滞BAM神经网络状态估计器的设计

刘佳，张运喜

（天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津300222）

摘要：基于Lyapunov-Krasovskii稳定性理论和积分等式的方法，给出闭环误差系统全局渐近稳定的时滞依赖充分条件，进一步得到状态估计器增益矩阵的表示方法，从而完成对中立型时变时滞BAM神经网络状态估计器的设计，通过仿真算例验证了所得结论的正确性和有效性。

关键词：双向联想记忆（BAM）神经网络；状态估计器；Lyapunov-Krasovskii泛函；时变时滞；中立型

1987年，Kosko[1]提出双向联想记忆神经网络模型。双向联想记忆（bidirectional associative memory，BAM）神经网络由2层双向联想回路构成，可根据存储记忆中的某些清晰或完整的模式对一些模糊或不完整的模式进行联想。BAM神经网络在模式辨识、自动控制、人工智能等工程领域中具有广泛的应用。实际应用中，人工神经网络的实现大多以电子电路为基础，电路中放大器和电容器的交换速度有限，导致人工神经网络中存在时间延迟现象，即时滞行为。人们对现代大规模集成电路研究发现，除了时滞行为外，系统过去的变化对现在状态也产生影响，这就是大规模集成电路的中立行为，而描述该现象的有力数学模型正是中立型微分方程。中立时滞的存在对系统的性能产生很大影响，因此对中立时滞神经网络的研究具有重要的理论和实践意义。然而，目前很少有科研人员涉及中立型时滞神经网络的研究[2-4]，且现有的研究中考虑的是中立时滞与状态时滞相等的情况，这在实际应用时存在局限性。

近年来，由于神经网络在实践中的成功应用，越来越多的研究人员开始关注神经网络的相关问题及应用。遗憾的是，神经元的状态通常不能完全测得，这给许多实际应用带来很大障碍，解决这一问题的方法就是设计神经网络的状态估计器，用来观测网络系统中每个神经元的状态。目前，这一问题的研究已取得一定进展[5-8]，但主要针对简单的单层神经网络进行状态估计，未涉及具有2层联想回路的BAM神经网络系统的状态估计设计问题。本文针对所考虑的BAM网络模型，建立新的Lyapunov-Krasovskii泛函，利用其稳定性理论和积分等式，给出系统状态估计器的存在条件，并进一步得到状态估计器的设计方法，通过一个仿真算例验证了所得给结论的正确性与有效性。

1　模型描述及预备知识

1.1模型描述

考虑中立型时变时滞BAM神经网络模型如下：

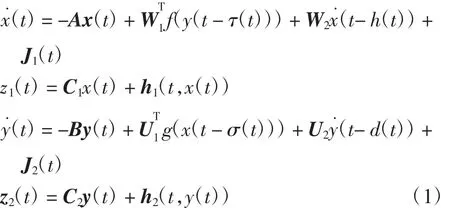
式中：x（t）= [x1（t），x2（t），…，xn（t）]T∈Rn和y（t）= [y1（t），y2（t），…，ym（t）]T∈Rm为神经元的状态向量；z1（t）和z2（t）为状态输出向量；f（·）= [f1（·），f2（·），…，fm（·）]T∈Rm和g（·）= [g1（·），g2（·），…，gn（·）]T∈Rn为神经元的激励函数；J1（t）= [J11（t），J12（t），…，J1m（t）]T和J2（t）= [J21（t），J22（t），…，J2m（t）]T为随机变化的输入向量；A=diag（a1，a2，…，an）>0和B=diag（b1，b2，…，bm）>0为正定对角矩阵；W1=（w1ij）m×n、W2=（w2ij）n×n、U1=（u1ij）n×m、U2=（u2ij）m×m为神经元之间关系连接权值矩阵；h1（t，x （t））= [h11（t，x（t）），h12（t，x（t）），…，h1n（t，x（t））]T∈Rn和h2（t，x（t））= [h21（t，x（t）），h22（t，x（t）），…，h2m（t，x（t））]T∈Rm为网络输出；C1> 0、C2> 0为正定对角矩阵；τ（t）、σ（t）为时变状态时滞；h（t）、d（t）为时变中立时滞。

本文有如下假设：

（A1）：时变时滞τ（t）、σ（t）、h（t）、d（t）均为可微函数，且对所有的t > 0以及给定常数τ> 0、σ> 0、h > 0、d > 0、τd> 0、σd> 0、hd> 0、dd> 0，满足如下不等式：

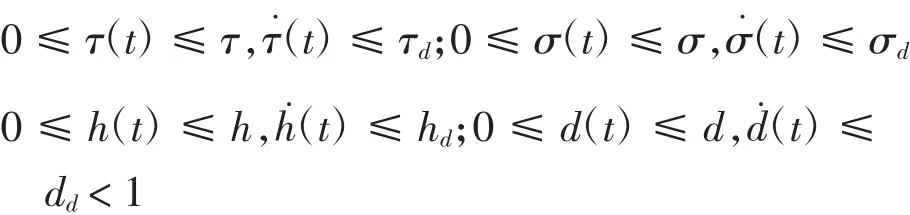
（A2）：fi（·）、gj（·）、h1j（·）、h2i（·）满足Lipschitz条件，即对任意x、y∈R和正数pi、qj、l1i、l2i（i = 1，2，…，m；j = 1，2，…，n），都有

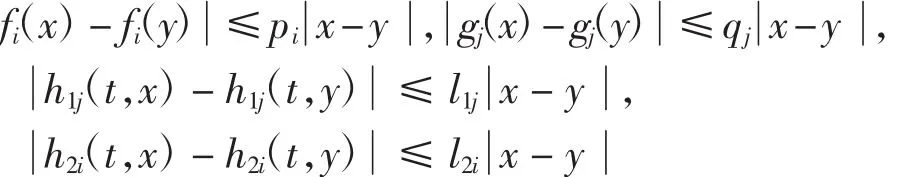
本研究的主要目的是设计一个状态估计器，用来有效观测神经元的状态，这个观测器中包含已知的网络输出。下面给出所设计的状态估计器的形式：

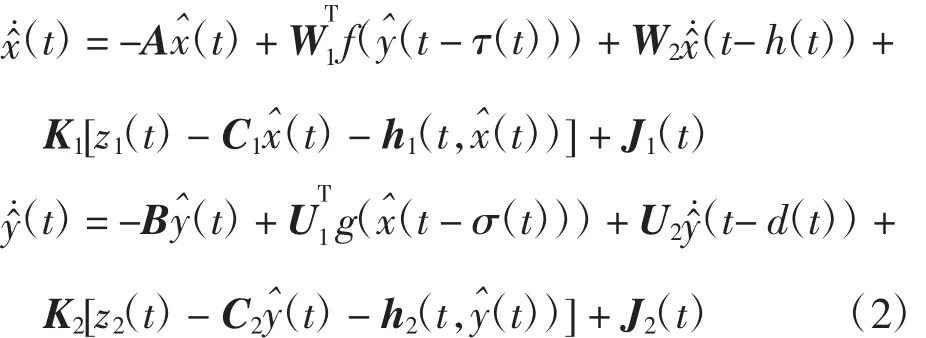
定义系统的状态误差为：

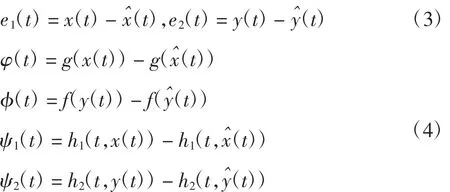
则误差系统可描述为：

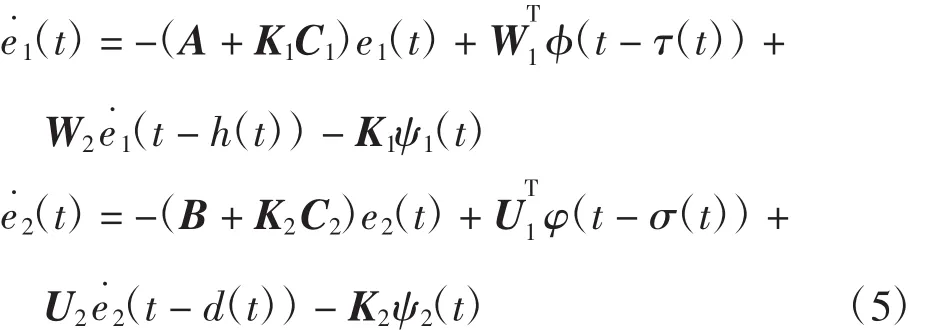
1.2预备知识

引理1（积分等式）对于适当维数任意矩阵R、M、X和向量函数f（s）、ξ，以下等式成立：

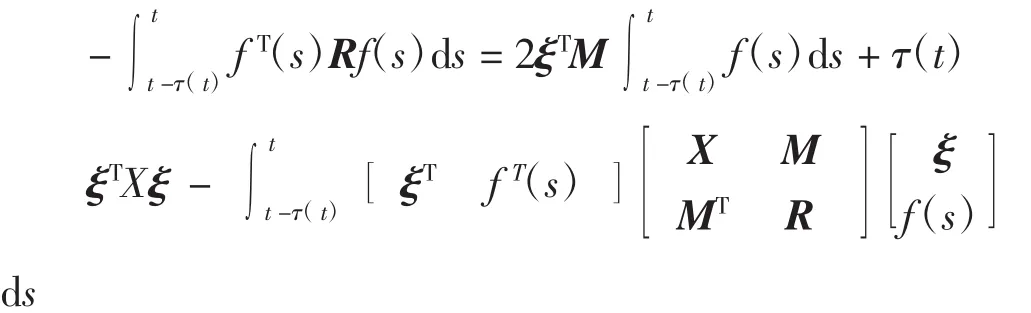
引理2（Schur补公式[9]）对给定的对称矩阵，S =

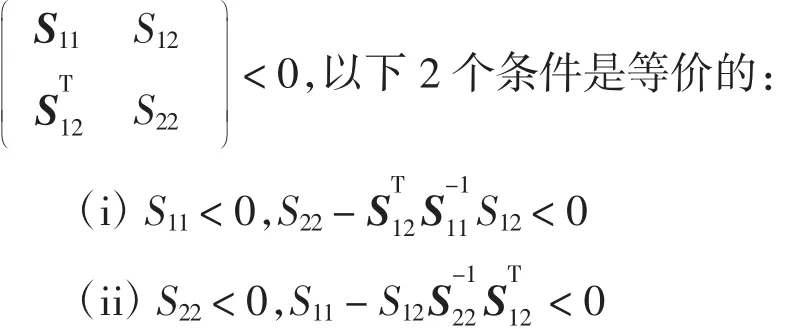
2　状态估计器设计

下面给出误差系统（5）的全局渐近稳定充分条件，并得到状态估计器（2）中增益矩阵的设计方法。

定理1假设（A1）-（A2）成立，如果存在适当维数的正定矩阵P1、P2、Q1、Q2、Q3、Q4、R1、R2、S1、S2，对角矩阵Ti> 0（i = 1，2，3，4）及矩阵Mj、Nj（j = 1，2，…，6），Y1、Y2，使以下不等式成立：

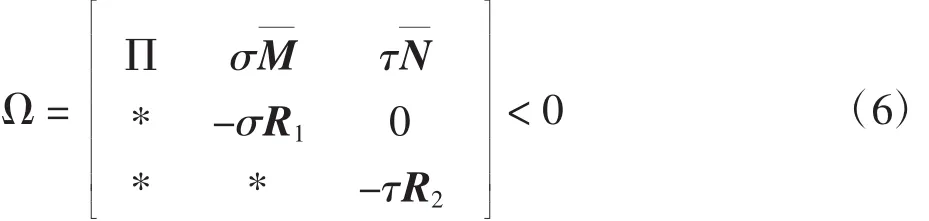
其中：

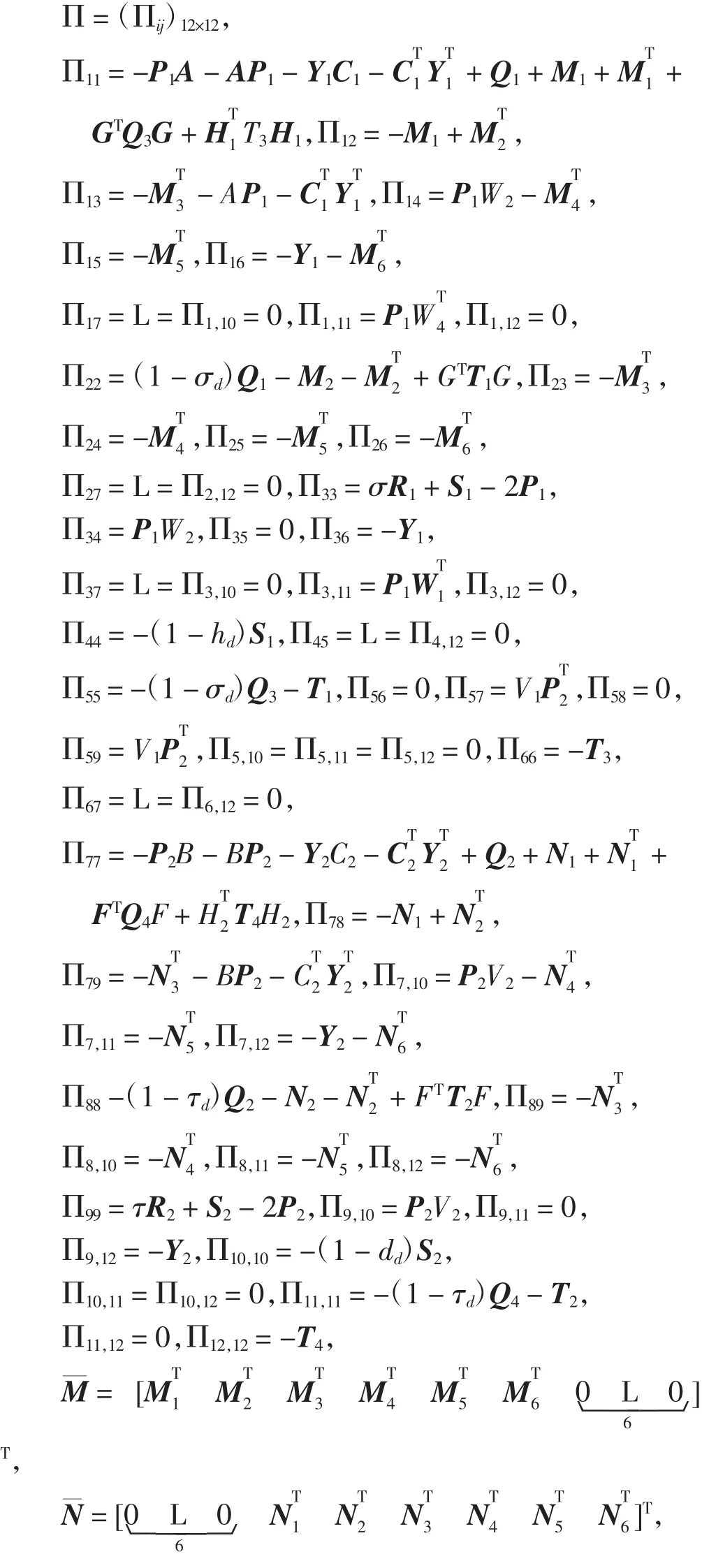
则误差系统（5）是全局渐近稳定的。状态估计器（2）的增益矩阵K1和K2可表示为：

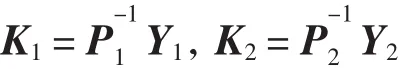
证明：选取Lyapunov -Krasovskii泛函

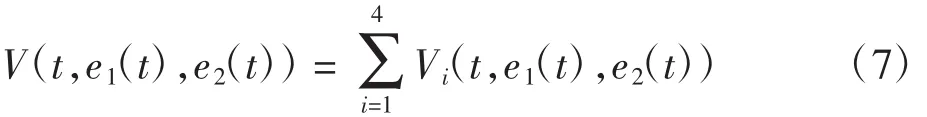
其中：

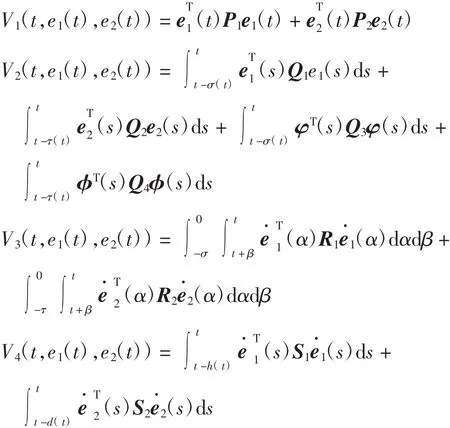
计算V（t，e1（t），e2（t））沿系统（5）的导数，可得

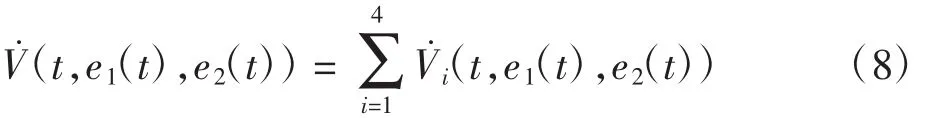
其中：

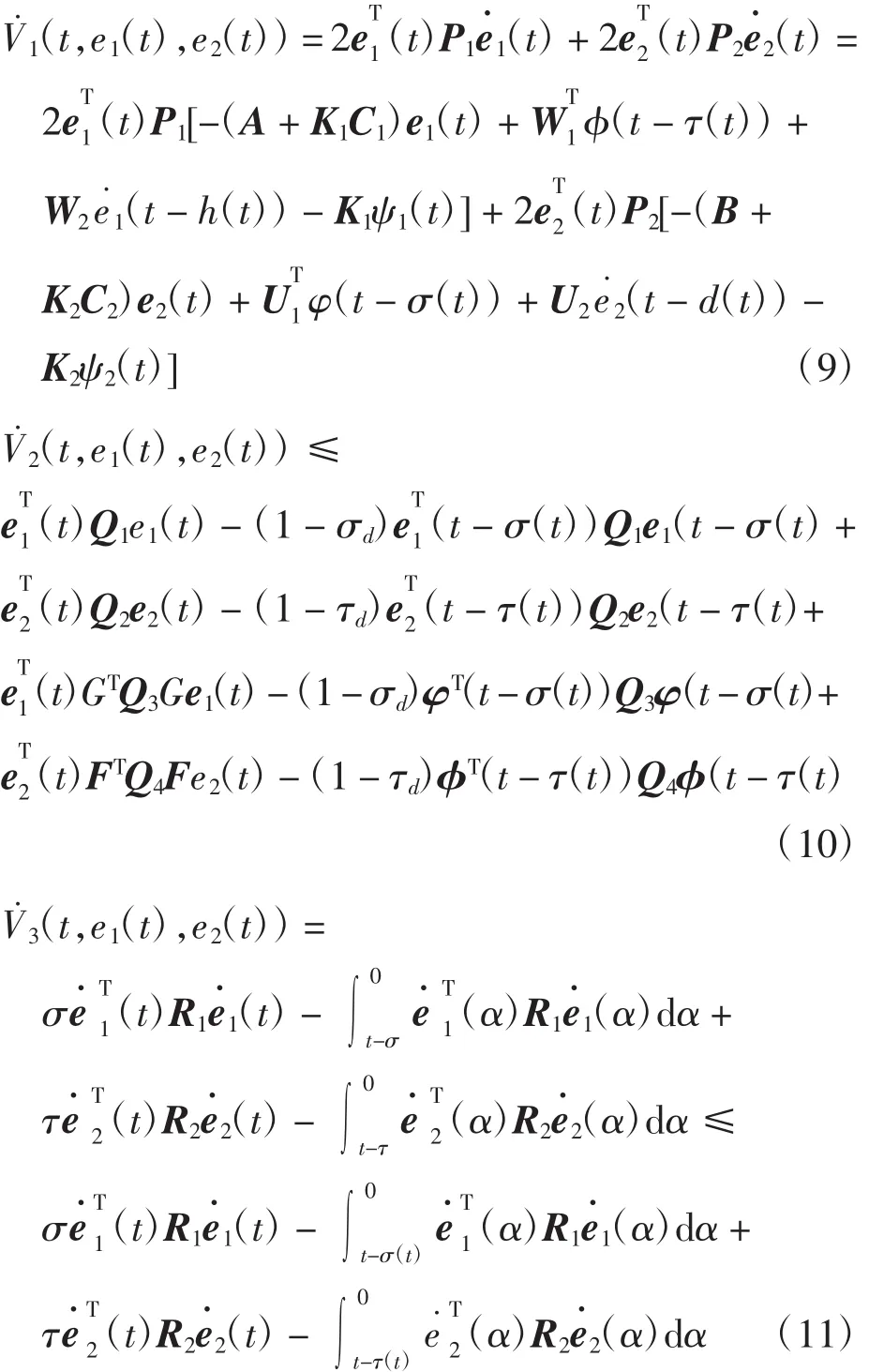
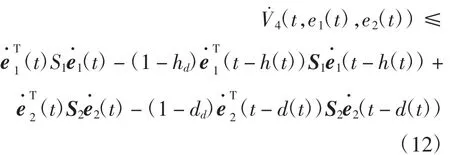
根据引理1可知，存在适当维数矩阵X、Y及

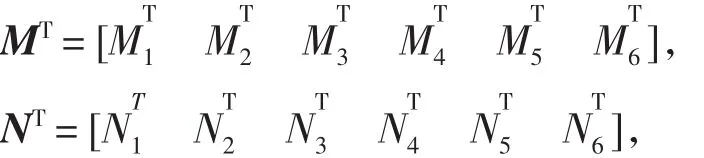
使

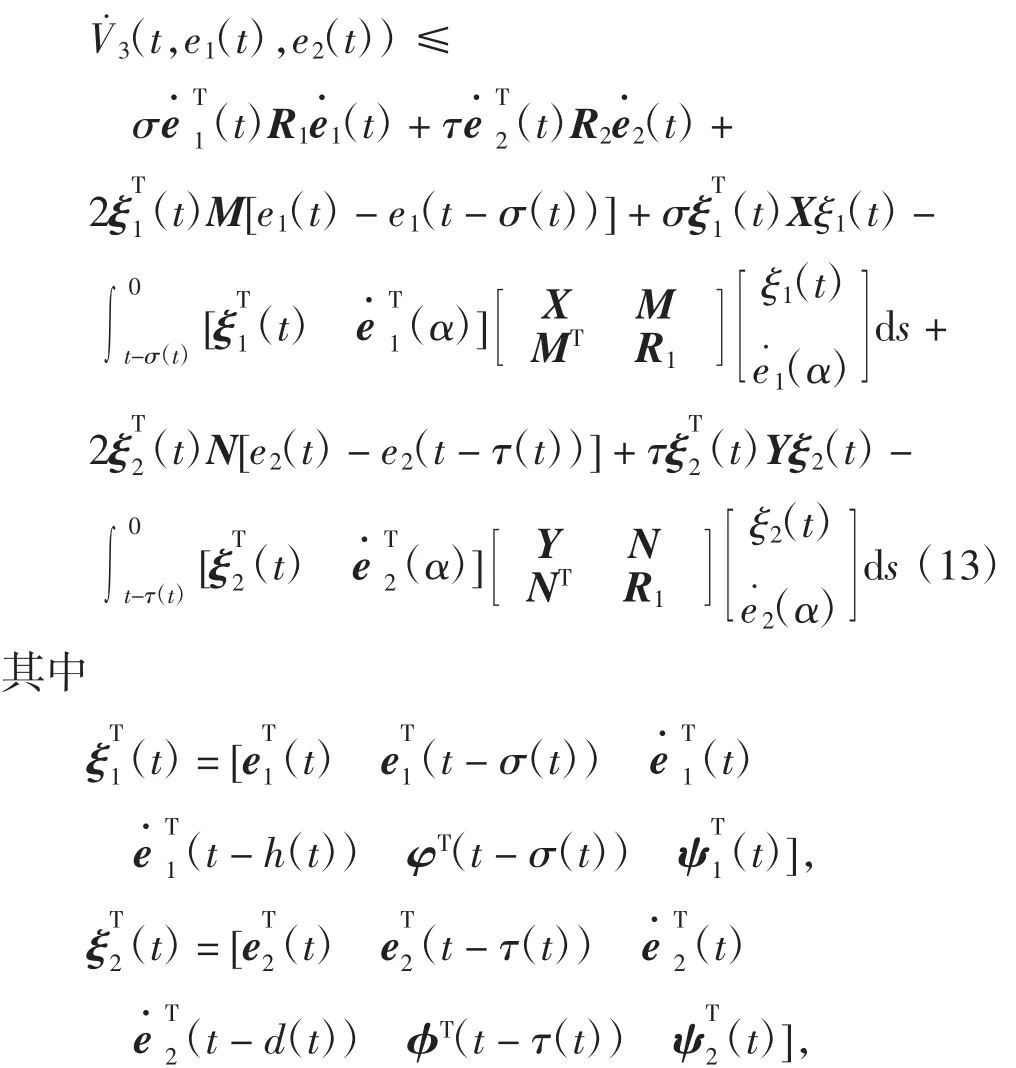
由（A2）可知，对于对角矩阵Ti> 0（i = 1，2，3，4），有

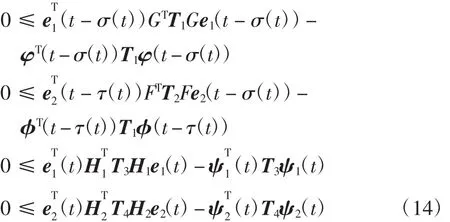
由误差系统（5），可以得到

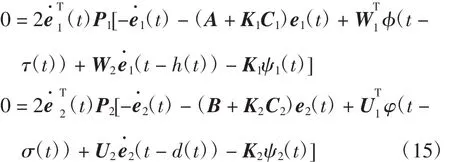
把式（9）—式（15）代入式（8），得

其中，ηT（t）= [ξT1（t）ξT2（t）]。

取X = MR-11MT，Y = NR-21NT，可以确保

根据Schur补引理可知，Ω< 0等价于

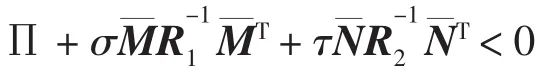
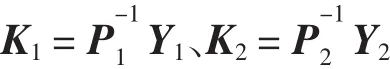
3　数值仿真

考虑具有如下参数的BAM神经网络系统：

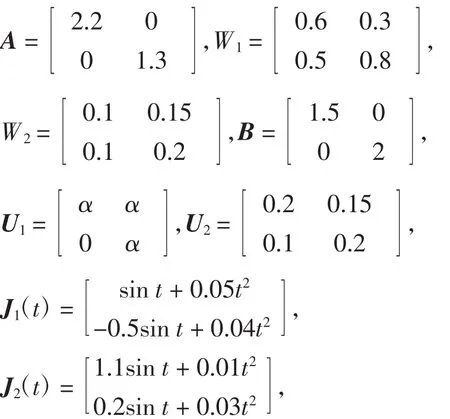
α> 0，C1= C2= I，F = G = 0.5I，H1= H2= 0.2I。

当α≤5.546时，定理1对于任意常时滞都成立。若取τ（t）=σ（t）= 5、h（t）= d（t）= 2、α= 5，应用定理1可求得状态估计器参数为：

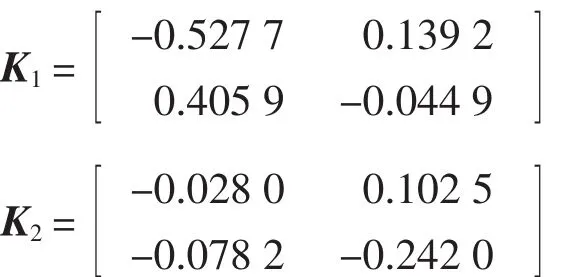
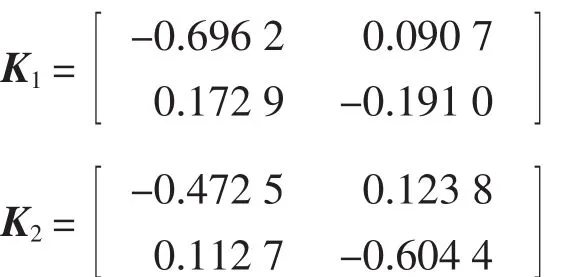
当α= 0.2、τ=τd= 1.5、σ=σd= 1.2、h = hd= 0.3、d = dd= 0.5时，即系统的状态时滞和中立时滞均为可变函数，根据定理1可求得状态估计器参数为：

状态变量x1（t）、x2（t）、y1（t）、y2（t）及其估计的时间响应情况如图1和图2所示。

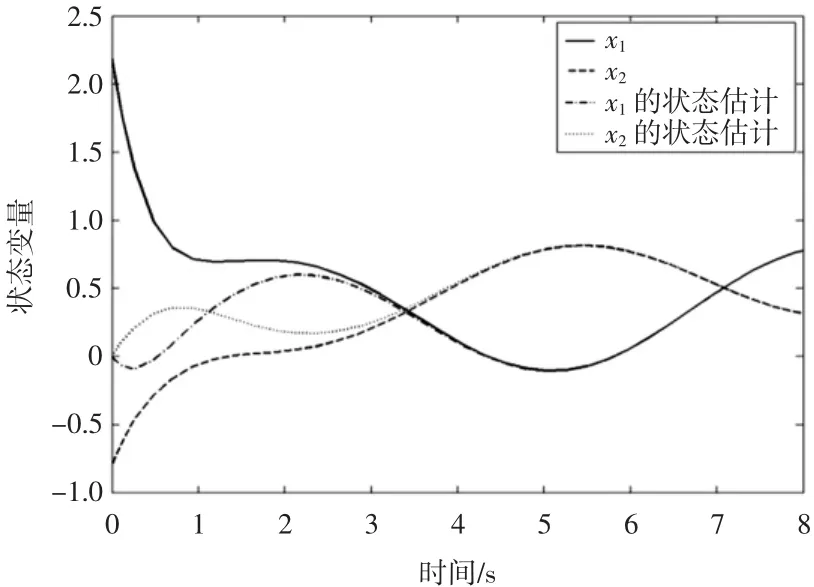
图1　状态变量x1（t）、x2（t）及其估计的时间响应

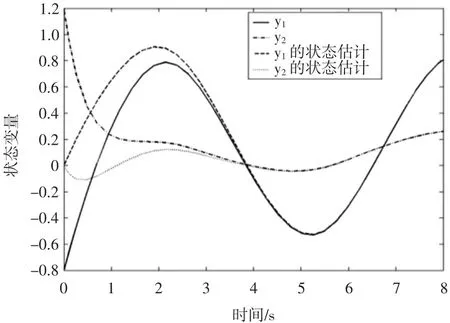
图2　状态变量y1（t）、y2（t）及其估计的时间响应

4　结束语

本文讨论了中立型时变时滞BAM神经网络的状态估计器设计方法。考虑中立型时变时滞和状态时变时滞不相等的情况，利用Lyapunov稳定性理论，以线性矩阵不等式的形式给出使闭环误差系统全局渐近稳定的充分条件，进而得到状态估计器增益矩阵的求解方法，完成对BAM神经网络的状态估计器设计。数值仿真表明，本文所得结论可行并具有广泛的应用价值。

参考文献：

［1］KOSKO B.Bidirectional associative memories［J］.IEEE Transactions Systems.Man Cybernet，1988，18：49-60.

［2］LIU J，ZONG G.New delay-dependent asymptotic stability conditions concerning BAM neural networks of neutral type ［J］.Neurocompting，2009，72：2549-2555.

［3］PARK J，PARK C，KWON O，et al.A new stability criterion for bidirecrtional associative Memory neural networks of neutral-type［J］.AppliedMathematicsandComputation，2008，199（2）：716-722.

［4］ZHAO Z，J IAN J，WANG B.Global attracting sets for neutral-type BAM neural networks with time -varying and infinite distributed delays［J］.Nonlinear Analysis Hybrid Systems，2015，15：63-73.

［5］ARUNKUMAR A，SAKTHIVEL R，MATHIYALAGN K，et al.Robust state estimation for discrete-time BAM neural networks with time-varying delay［J］.Neuroco-mputing，2014，131（5）：171-178.

［6］SAKTHIVEL R，VADIBEL P，MATHIYALAGN K，et al.Design of state estimator for bidirectional associative memory neural networks with leakage delays［J］.Information Sciences，2015，296（1）：263-274.

［7］PARK J，KWON O.Design of state estimator for neural networks of neutral-type［J］.Appl Math Comput，2008，202：360-369.

［8］WANG Z，HO D，LIU X.State estimation for delayed neural networks［J］.IEEE Trans Neural Networks，2005，16（1）：279-284.

［9］俞立.鲁棒控制-线性矩阵不等式处理方法［M］.北京：清华大学出版社，2002.

Design of state estimator for BAM neural networks with time-varying delays of neutral type

LIU Jia，ZHANG Yun-xi
（Tianjin Key Laboratory of Information Sensing and Intelligent Control，Tianjin University of Technology and Education，Tianjin 300222，China）

Abstract：Based on Lyapunov-Krasovskii theory and integral equality approach，the delay-dependent sufficient condition is obtained to ensure the closed-loop error system is globally asymptotically stable.Furthermore，the gain matrices of the estimator can be determined and the state estimator is designed completely.Finally，a numerical example is provided to demonstrate the effectiveness of the proposed method.

Key words：bidirectional associative memory（BAM）neural networks；state estimator；Lyapunov-Krasovskii functional；time-varying delays；neutral type

作者简介：刘佳（1982—），女，讲师，研究方向为非线性系统控制.

基金项目：国家自然科学基金资助项目（61304153）；天津市应用基础与前沿技术研究计划青年项目（15JCQNJC04200）；天津市高等学校科技发展基金资助项目（20120828）；天津职业技术师范大学科研启动基金资助项目（KYQD12013）.

收稿日期：2015-11-20

中图分类号：TP183

文献标识码：A

文章编号：2095－0926（2016）01－0058－05