基于频率域奇异值分解的地震数据插值去噪方法研究

马继涛,王建花,刘国昌

(1.中国石油大学(北京)地球物理与信息工程学院物探系,北京102249;2.中海油研究总院,海洋石油勘探国家工程实验室,北京100028)



基于频率域奇异值分解的地震数据插值去噪方法研究

马继涛1,王建花2,刘国昌1

(1.中国石油大学(北京)地球物理与信息工程学院物探系,北京102249;2.中海油研究总院,海洋石油勘探国家工程实验室,北京100028)

摘要:奇异值分解(Singular Value Decomposition,SVD)是近几年发展起来的一种地震数据随机噪声压制方法。基于频率域奇异值分解矩阵降秩运算,利用凸集投影(Projection Onto Convex Sets,POCS)迭代算法,实现了地震数据去噪和插值的同步处理,给出了方法的实现步骤。实际资料处理时，采用分窗处理方式减少了算法对内存的需求,降低了插值和去噪处理的运算量,同时使有效信号的同相轴线性化,满足方法的假定条件。模拟数据和实际资料测试均表明,频率域奇异值分解方法可以在压制地震数据噪声的同时进行插值处理,具有广阔的应用前景。

关键词：奇异值分解(SVD);频率域;插值;去噪

奇异值分解(SVD)是提高地震资料信噪比的有效手段之一,被广泛应用于VSP波场分离、地震信号增强等。SERGIO等[1]首先提出基于K-L变换的奇异值分解方法,通过特征图像滤波分离VSP波场。高静怀等[2]、徐伯勋等[3]指出,从图像处理的角度看,奇异值分解相当于K-L变换。针对奇异值分解仅能提高水平同相轴信噪比、不能有效确定奇异值分解滤波参数等问题,陈遵德等[4]、陆文凯等[5]对SVD滤波方法做了一些改进。吴亚东等[6]改进了奇异值分解滤波方法,使其对脉冲干扰、侧反射以及其它反向干扰的压制效果更好。李文杰等[7]提出利用奇异值分解滤波法衰减地震记录中的直达波和折射波。2009年,SACCHI[8]研究了基于奇异谱分析(频率域奇异值分解)的地震数据随机噪声压制技术。魏小强等[9]基于多道奇异谱分析理论,对三维地震数据进行了插值重建,但是没有涉及地震数据去噪问题。黄建平等[10]基于奇异谱分析理论对三维地震数据进行去噪和插值,但未对反对角线平均的问题加以阐述。

频率域奇异值分解压制地震数据随机噪声的原理相对简单:如果不含噪声的地震数据由k个线性同相轴组成,则其对应频率域的Hankel矩阵的秩应为k;若地震数据中存在随机噪声,则该矩阵的秩会增加。因此,通过降秩处理可以压制地震数据中的随机噪声。同样,地震数据有缺失道也会使Hankel矩阵的秩增加,因此,通过降秩处理还可以对地震数据进行插值。本文基于频率域奇异值分解理论,研究了地震数据插值和去噪同步处理方法,并对奇异值分解降秩处理后的反对角线平均问题做了详细阐述。理论数据和实际资料的测试结果表明方法具有可行性与有效性。

1方法原理

1.1基于频率域奇异值分解的插值去噪原理

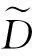
(1)一般取M=E(N/2)+1,该矩阵反对角线上的元素相同。若某一线性同相轴在时间域为:

(2)式中:t为时间,x为偏移距,p为线性同相轴的斜率,w为地震子波。经过傅里叶变换,(2)式在频率域可表示为:

(3)对于规则排列的地震数据,偏移距x=nΔx,其中n为地震道序号。令α=ωpΔx,则公式(3)又可表示为:

(4)简写为:

(5)由Fn和Fn-1可以得到信号的一阶差分方程预测形式:

(6)将F1～Fn代入矩阵H中(公式(1)),此时矩阵H的秩为1。同理,当地震剖面中含k个线性同相轴时,存在方程:

(7)此时,矩阵H的秩为k。因此,可以用前k个奇异值对地震数据中的有效信号进行重构,从而压制不相关的随机噪声。

由上述推导可以看出,若地震记录中只含有一个线性同相轴且不含噪声,则此地震记录对应Hankel矩阵的秩为1;同样,若地震记录含有k个线性同相轴且不含噪声,对应Hankel矩阵的秩为k。地震数据中存在的随机噪声会使Hankel矩阵的秩增加,利用奇异值分解对Hankel矩阵做降秩处理可以滤除随机噪声。类似地,地震数据若有地震道缺失,则缺失的地震道在数据矩阵中对应列的数值为0。将缺失的地震道变换到f-x域时,其对应频率域的样点数值仍然为0。这些0值样点变换到Hankel矩阵中后,会使矩阵的秩增加。因此,地震数据缺失时,降秩处理的目的是得到一个与原Hankel矩阵类似、没有缺失道的低秩矩阵。

利用频率域奇异值分解对地震记录中的缺失道进行插值与随机噪声压制的过程是类似的,因此两种处理可以同时进行。本文随机噪声压制和缺失地震道插值的步骤如下:

1) 通过傅里叶变换将地震数据转换至f-x域;

2) 将每个频率分量转变为Hankel矩阵;

3) 通过奇异值分解,得到奇异值谱;

4) 对Hankel矩阵进行降秩处理;

5) 沿Hankel矩阵反对角线方向求取平均值并转换为频率域地震道数据;

6) 通过傅里叶反变换将频率域地震道数据转换至时间域,完成去噪、插值处理。

1.2反对角线平均处理

在利用频率域奇异值分解进行去噪、插值的过程中,若降秩处理后的矩阵仍然是Hankel矩阵,则将Hankel矩阵转变为频率域地震道数据之后,通过傅里叶反变换就可以得到去噪和插值后的时间域数据。假定s为降秩后的频率域数据,那么s(n)可以从降秩后Hankel矩阵H′的反对角线元素得到,反对角线上矩阵元素的序号i,j满足i+j-1=n。如s(1)可以由降秩后Hankel矩阵的元素H′(1,1)得到,s(2)可以由降秩后Hankel矩阵的元素H′(1,2),H′(2,1)得到。但在实际数据处理中,降秩后得到的矩阵一般不再是Hankel矩阵,需要沿反对角线方向求取矩阵元素平均值,以得到规则的Hankel矩阵。GOLYANDINA等[11]引入了一个能在降秩后求取矩阵反对角线元素平均值的算子。为简化对算子的描述,假设Hankel矩阵H(L,K)中,L≤K,令i+j-1=n,J=L+K-1,则降秩后的频率域数据s(n)可以由以下公式计算得到:

(8)

利用公式(8),可由降秩处理后的矩阵恢复去噪和插值后的频率域数据s。

1.3POCS迭代算法

若只对地震数据进行去噪处理,则利用公式(8) 恢复频率域数据,并通过傅里叶反变换至时间域后,可得到去噪后的地震数据;若对地震数据去噪的同时进行插值处理,则利用公式(8)恢复频率域数据,并通过傅里叶反变换至时间域后,会在空地震道处出现一些降低矩阵秩的数值,这些数值比其它地震道振幅要小。为得到空地震道处的正确振幅,本文利用POCS算法进行迭代处理[12]。在f-x域进行POCS迭代处理,可以在恢复空地震道正确振幅的同时,保持原有数据的振幅特性。

假定输入数据S是二维数据,建立一算子T,其作用是在插值后识别空地震道的位置,并提取插值前正常的地震道,将其放在原处。正常地震道处T(i,j)=1,空地震道处T(i,j)=0。将算子T作用于数据S,得到数据Sobs,即Sobs=T·S。可以看出,Sobs=T·Sobs。

2.3.5 非心脏外科手术：为减少外科手术围术期心脏并发症风险，在术前应首先评估外科手术的紧迫性、出血风险和心血管事件的发生风险。在充分权衡出血和血栓风险的基础上，围手术期抗血小板治疗应由多学科(外科医师、麻醉师、心内科医生)和患者共同决定：出血危险较低的患者，可继续服用阿司匹林。如患者进行小型牙科手术、皮肤科操作、白内障手术等出血风险低的手术；手术相关出血风险高，应术前停用抗血小板药物，通常术前停用P2Y12受体拮抗剂至少5d，术前需停用所有抗血小板治疗的患者，如遇到血栓风险高患者，可给予静脉抗血小板药物GPⅡb/Ⅲa 受体拮抗剂或低分子肝素“桥接”。

对重建后的数据再次进行频率域奇异值分解降秩处理,并将原正常的地震道再次放回原处,如此迭代直至缺失地震道振幅满足设定的条件为止。假定I是与T大小相同且元素全为1的矩阵,则利用POCS迭代和奇异谱分析进行去噪、插值的算法如下:

forp=1∶N

(9)

end

end

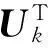
因实际地震资料数据量较大,利用本算法进行插值和去噪时,奇异值分解对内存的需求及计算量均非常大;同时实际资料并不完全满足本方法假定有效信号是线性且平稳信号的条件。为减少算法对内存的需求,降低插值和去噪的运算量,同时使有效信号的同相轴线性化,本文对数据进行分窗处理。一般而言,分窗可以加快运算速度,使地震数据的同相轴局部线性化和平稳化,但窗口选取过大,会影响信号的局部线性化和平稳化,使窗口内大部分同相轴不满足方法的假定条件,从而导致处理效果变差。窗口选取过小,很明显会增加运算量。因此,窗口的空间宽度和时间长度选取要适中,需根据实际数据的复杂程度进行最优化选择。

2模拟数据测试

2.1有效性验证

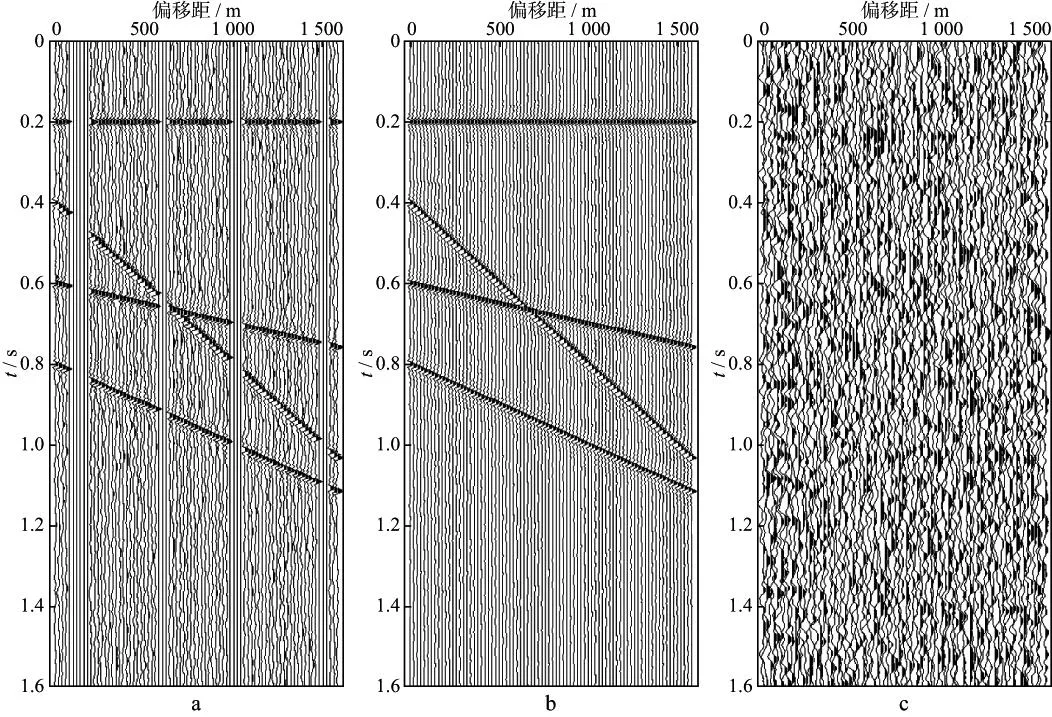
图1　模拟数据迭代6次插值去噪处理前后对比(信噪比为5)a 处理前的数据; b 插值去噪后的结果; c 压制掉的噪声

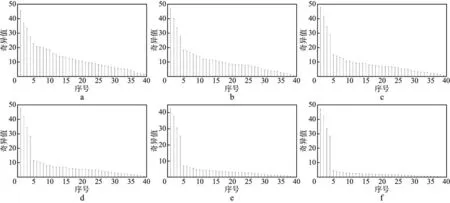
图2　模拟数据迭代处理过程中的奇异值分布a 第1次迭代; b 第2次迭代; c 第3次迭代; d 第4次迭代; e 第5次迭代; f 第6次迭代

2.2抗噪性分析

为测试本文插值去噪方法的适用性,对图1所示模拟数据分别加入一定程度的随机噪声,加噪后数据的信噪比分别为2,1(有效信号最大振幅与随机噪声最大振幅比值分别为2,1)。利用本文方法对其进行插值去噪处理,同样迭代6次,信噪比为2的数据处理结果如图3所示,信噪比为1的数据处理结果如图4所示。从图3和图4可以看出,即使在数据信噪比为1的情况下,本文方法仍然能够在重建出空缺地震道的同时,有效压制随机噪声。但同时可以看出,数据中噪声能量较强时(图4),去噪并重建后的结果中仍残存部分随机噪声。进一步测试表明,增加迭代次数可改善噪声压制效果。因为增加迭代次数可进一步降低矩阵的秩,进一步压制随机噪声。

2.3重建效果分析

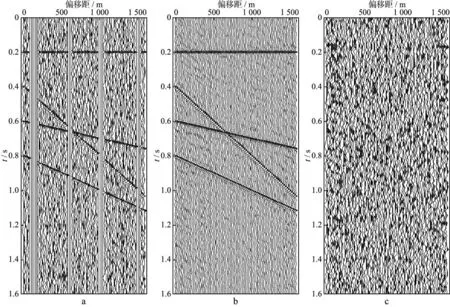
图3　模拟数据迭代6次插值去噪处理前后对比(信噪比为2)a 处理前的数据; b 插值去噪后的结果; c 压制掉的噪声

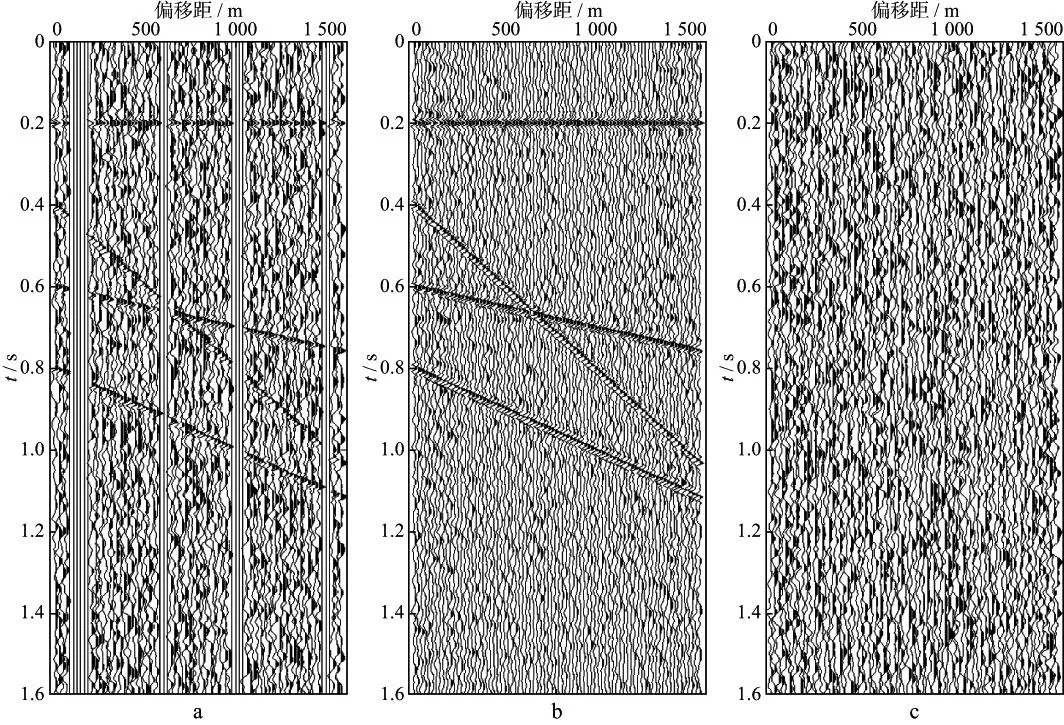
图4　模拟数据迭代6次插值去噪处理前后对比(信噪比为1)a 处理前的数据; b 插值去噪后的结果; c 压制掉的噪声

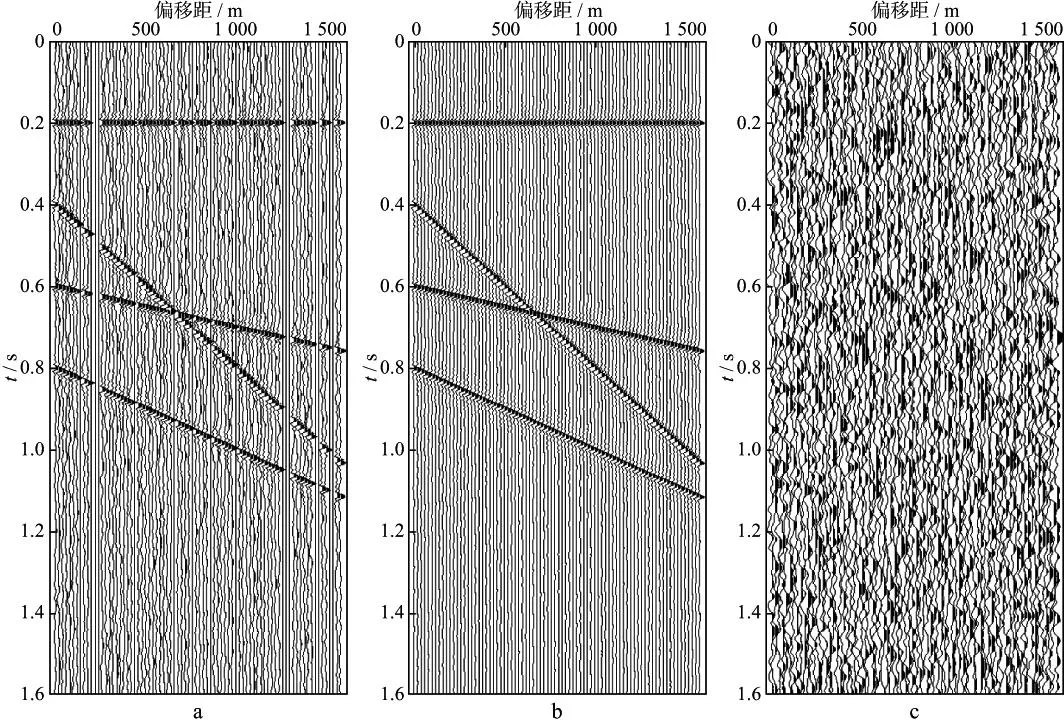
图5　随机空缺20道的模拟数据迭代10次插值去噪处理前后对比(信噪比为5)a 处理前的数据; b 插值去噪后的结果; c 压制掉的噪声

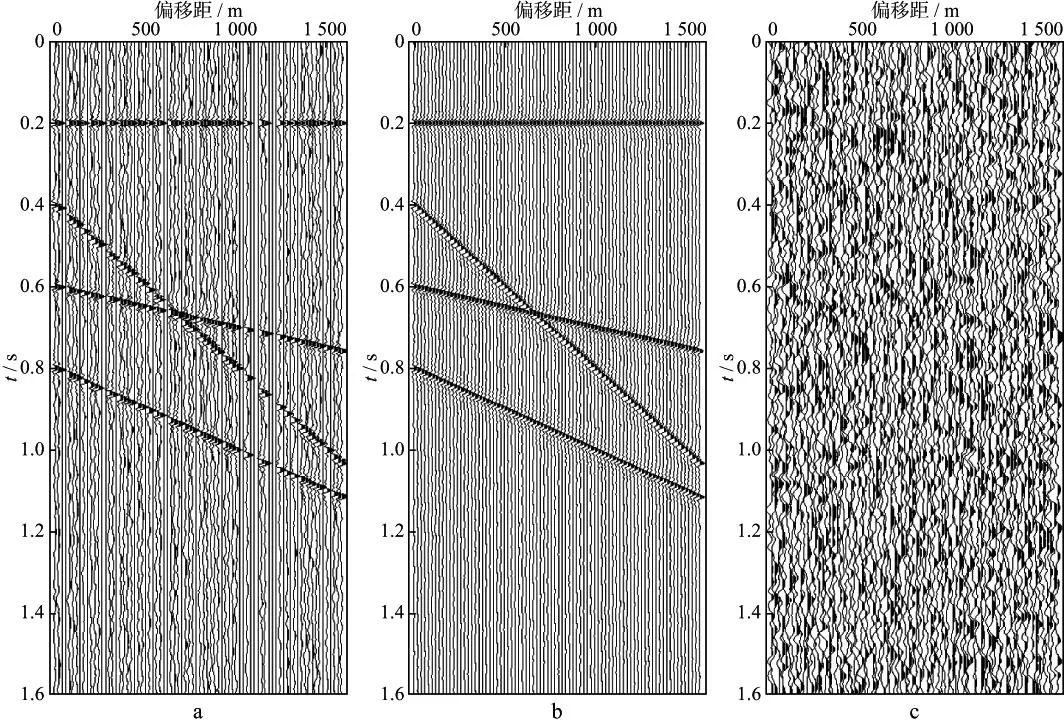
图6　随机空缺40道的模拟数据迭代10次插值去噪处理前后对比(信噪比为5) a 处理前的数据; b 插值去噪后的结果; c 压制掉的噪声

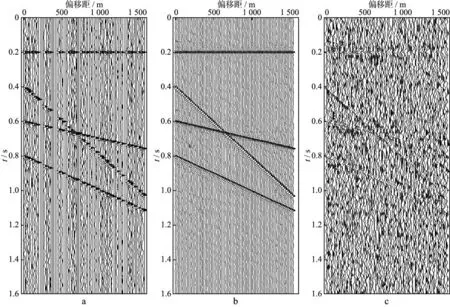
图7　随机空缺60道的模拟数据迭代10次插值去噪处理前后对比(信噪比为5)a 处理前的数据; b 插值去噪后的结果; c 压制掉的噪声

对含噪声且地震道缺失程度不同的数据进行重建和去噪效果对比测试。模拟数据总道数为80,对其加入一定量的随机噪声,并随机删除其中的20,40和60道,最大连续空道个数为7道,最小连续空道个数为1道。利用前述频率域奇异值分解插值去噪方法对其进行插值去噪处理,迭代次数均为10次,处理结果分别如图5,图6和图7所示。可以看出,即使在地震道缺失程度高达75%的情况下,本文方法仍然可以较好地完成对地震数据的重建和去噪处理。然而从图7c可以明显看出,空缺60道的模拟数据插值去噪结果与原始数据之差存在一些有效波的信息,说明重建后数据与原始数据之间存在一定程度的差异。将图7中的模拟数据迭代次数增加到30次后,差异剖面中基本看不到有效波信息(图8),说明增加迭代次数可以改善最终的插值去噪处理效果。

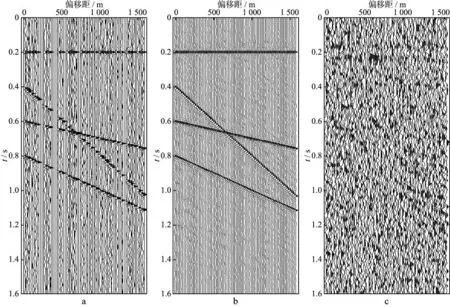
图8　随机空缺60道的模拟数据迭代30次插值去噪处理前后对比(信噪比为5)a 处理前的数据; b 插值去噪后的结果; c 压制掉的噪声

3实际资料测试处理

用南海某区实际资料对本文方法进行了测试。考虑实际资料数据量大,采用滑动分窗处理方式,每个窗口的大小相同,为横向100个样点,纵向100个样点。在每个窗口内同相轴可近似视为线性的。数据除自身存在着随机噪声外,还被随机删除了50道,删除的地震道中,最大连续空道个数为8道。图9a为缺失50道的地震数据,图9b为应用本文方法迭代8次插值去噪后的结果,图9c为去除的随机噪声,运算中选取奇异值的个数为12个。从图9b和图9c可以看出,本文方法较好地重建了缺失的地震道,压制的噪声除了随机噪声之外,还有部分绕射噪声。为了更好地展示本文方法的插值去噪效果,对图9中的局部区域进行放大显

示。图10展示了图9中虚线框内数据的重建及去噪结果,图11展示了图9中实线框内数据的重建及去噪结果。由图10和图11可以看出,重建后的信号同相轴连续,并且具有更高的信噪比。

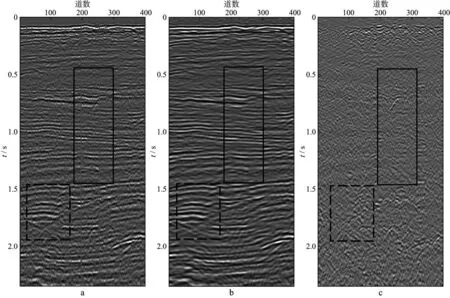
图9　实际地震资料插值去噪处理前后对比a 处理前的剖面; b 插值去噪后的结果; c 压制掉的噪声

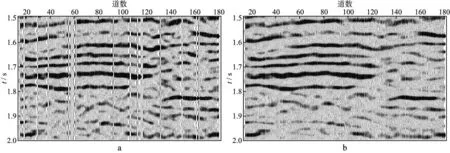
图10　实际地震剖面局部放大(针对虚线框)a 处理前的剖面; b 插值去噪后的结果

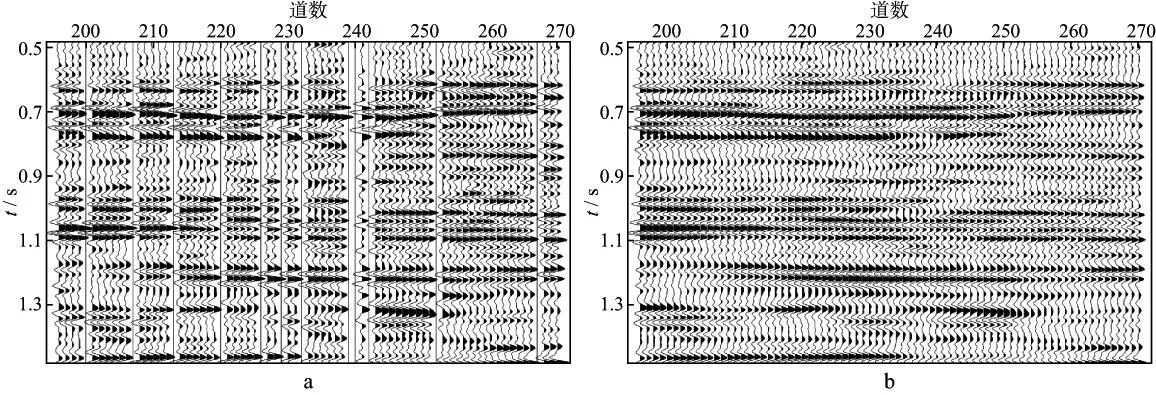
图11　实际地震剖面局部放大(针对实线框)a 处理前的剖面; b 插值去噪后的结果

4结论与建议

本文基于频率域奇异值分解实现了地震数据插值和去噪的同步处理,并用模拟数据和实际资料对方法进行了验证。通过分析和研究,得到以下结论与建议:

1) 噪声的存在和地震道的缺失会影响地震数据中奇异值的分布,在频率域对数据矩阵进行降秩可实现地震数据去噪和插值的同步处理;

2) 为重建空缺地震道数据,同时保持原始数据的振幅特征,在降秩过程中需利用POCS算法进行迭代处理;

3) 对于数据量较大的实际地震资料,采用分窗方式进行处理可以减少算法对内存的需求和运算量,同时使有效信号的同相轴线性化。

参考文献

[1]SERGIO L M F,TAD J U.Application of singular value decomposition to vertical seismic profiling[J].Geophysics,1988,53(6):778-785

[2]高静怀,朱光明,王玉贵.奇异值分解在VSP中的应用[J].西安地质学院学报,1992,14(3):71-78

GAO J H,ZHU G M,WANG Y G.Application of singular value decomposition to VSP[J].Journal Xi’an College of Geology,1992,14(3):71-78

[3]徐伯勋,白应甫,白旭滨,等.奇异值分解在垂直地震剖面中的应用[J].石油物探,1993,32(3):60-72

XU B X,BAI Y F,BAI X B,et al.Application of singular value decomposition (SVD) to VSP[J].Geophysical Prospecting for Petroleum,1993,32(3):60-72

[4]陈遵德,段天友,朱广生.SVD滤波方法的改进与应用[J].石油地球物理勘探,1994,29(6):783-792

CHEN Z D,DUAN T Y,ZHU G S.Improvement of singular-value-decomposition filtering and the application[J].Oil Geophysical Prospecting,1994,29(6):783-792

[5]陆文凯,牟永光.一种改进的SVD滤波器[J].石油地球物理勘探,1996,31(5):736-741

LU W K,MOU Y G.An improved SVD filter[J].Oil Geophysical Prospecting,1996,31(5):736-741

[6]吴亚东,符溪,文鹏飞,等.奇异值分解压制随机噪声的方法及应用[J].新疆石油地质,2003,24(2):144-145

WU Y D,FU X,WEN P F,et al.SVD method and its application in attenuating Random noise[J].Xinjiang Petroleum Geology,2003,24(2):144-145

[7]李文杰,魏修成,刘洋,等.SVD滤波法在直达波和折射波衰减处理中的应用[J].石油勘探与开发,2004,31(5):71-73

LI W J,WEI X C,LIU Y,et al.Application of SVD filtering in the processing of decaying direct wave and refracted wave[J].Petroleum Exploration and Development,2004,31(5):71-73

[8]SACCHI M.FX singular spectrum analysis[R].Calgary,Alberta,Canada:CSPG CSEG CWLS Convention,2009:392-395

[9]魏小强,雷秀丽,马庆珍.基于多道奇异谱分析的三维地震数据规则化方法[J].石油地球物理勘探,2014,49(5):846-851

WEI X Q,LEI X L,MA Q Z.3D seismic data regularization based on multi-channel singular spectrum analysis[J].Oil Geophysical Prospecting,2014,49(5):846-851

[10]黄建平,李闯,李国磊,等.基于奇异谱分析的联合去噪及规则化方法[J].地球物理学进展,2014,29(4):1666-1671

HUANG J P,LI C,LI G L,et al.Simultaneous seismic data de-noising and regularization method based on singular spectrum analysis[J].Progress in Geophysics (in Chinese),2014,29(4):1666-1671

[11]GOLYANDINA N,NEKRUTKIN V,ZHIGLJAVSKY A.Analysis of time series structure:SSA and related techniques[M].Boca Raton,Fla:Chapman & Hall/CRC,2001:28-29

[12]ABMA R,KABIR N.3D interpolation of irregular data with a POCS algorithm[J].Geophysics,2006,71(6):E91-E97

(编辑：戴春秋)

Seismic data noise attenuation and interpolation using singular value decomposition in frequency domain

MA Jitao1,WANG Jianhua2,LIU Guochang1

(1.GeophysicsDepartment,CollegeofGeophysicsandInformationEngineering,ChinaUniversityofPetroleum,Beijing102249,China; 2.CNOOCResearchInstitute,OffshoreOilExplorationNationalEngineeringLaboratory,Beijing100028,China)

Abstract:Singular value decomposition (SVD) is a seismic random noise attenuation method developed in recent years.Using the rank reduction character of frequency singular value decomposition,and by a projection onto convex sets (POCS) iterative algorithm,a method that can simultaneously process seismic data interpolation and random noise reduction is realized,and the anti-diagonal averaging process is characterized in detail.Sliding window in real data processing can linearize the seismic events in the localized window,reduce the memory storage requirement,and decrease the computation cost.The method is tested with synthetic data and real datasets,and the results illustrate that the rank reduction method using singular value decomposition in the frequency domain can suppress seismic noise while interpolate seismic data well,which shows a broad application prospect.

Keywords:singular value decomposition (SVD),frequency domain,interpolation,noise attenuation

文章编号：1000-1441(2016)02-0205-09

DOI:10.3969/j.issn.1000-1441.2016.02.006

中图分类号：P631

文献标识码：A

基金项目：国家自然科学基金(41404099)、中国石油大学(北京)科研基金项目(2462015YQ0512)、海洋石油勘探国家工程实验室“斜缆采集地震数据分析与处理技术研究”项目联合资助。

作者简介：马继涛(1983—),男,博士,讲师,主要从事地震数据处理方法研究工作。

收稿日期：2015-05-07;改回日期：2015-10-25。

This research is financially supported by the National Natural Science Foundation of China (Grant No.41404099),the Science Foundation of China University of Petroleum,Beijing (Grant No.2462015YQ0512) and the Project from National Engineering Laboratory for Offshore Oil Exploration.